基于力系简化神经网络的过驱动控制分配

任军洲，蔡 勇，2，李自胜

（1.西南科技大学 制造科学与工程学院，绵阳 621000；2.制造过程测试技术省部共建教育部重点实验室，绵阳 621000）

在实际工程问题中，为了有更好的动态性能，一些设备存在过驱动情况。例如，矢量推进水下机器人[1-2]、四足机器人[3]、外太空卫星[4-5]、矢量多旋翼无人机[6]等。在过驱动系统中，解决控制分配一直是一个活跃的研究领域[7]。

目前，过驱动系统的控制分配方法包括二次规划、伪逆法、加权最小二乘法、神经网络等。其中，伪逆法在控制分配领域应用广泛。采用伪逆法，可以解决倾转旋翼机的控制分配、水下矢量推进器的控制分配；也可以实现全向空中机器人的控制分配[8]、分布式推进配置飞行器的控制分配[9]。但是，伪逆法的本质是固定分配，不能充分利用执行器冗余优势。

二次规划法能够实现动态分配。基于该方法，可以实现航天器姿态控制过程中的实时控制分配、过驱动UUV 推进器容错控制的非线性观测自适应推力分配[10]、多舵面飞翼布局飞机的控制分配[11]。该方法需要调整权重参数，在最小值和准确度之间找到一种平衡。然而固定的权重会引入偏见，导致内耗，体现在以最小消耗为目标时，并非最优分配方案。

随着神经网络技术的发展，直接利用神经网络解决控制分配成为一种新的可能，但相关研究较少。文献[12]结合了神经网络技术求解二次规划，解决控制分配。但是本质是利用递归思想求解，而不是直接利用神经网络分配；文献[13]采用自编码器结构训练神经网络解决了含有6 个控制舵面的空天飞行器控制分配。

本文结合空间任意力系简化原理和自编码器，提出一种力系简化神经网络结构，训练神经网络实现控制分配。

1 过驱动系统的控制分配

1.1 过驱动系统

不失一般性，动力学系统可以描述为

在该系统中，当CB行满秩时，系统控制存在过驱动[14]。

控制过驱动系统，首先由高级控制器规划参考运动轨迹；再根据被控物的目标位置Pt与当前位置Pr，利用PID 计算出系统目标控制量，假设为v；然后利用分配控制器将控制量分配给每个执行器，如式（2）所示：

式中：u为每个执行器控制分量写成的向量。对于过驱动系统，不能直接求得u的唯一结果。

1.2 控制分配

进一步整理得到：

式中：D=CB；x=u；b=v。其中，x是需要求解的未知变量。

D行满秩，则x存在多解，常用伪逆法和二次规划法求解。伪逆法是左乘D的伪逆矩阵；二次规划法是将式（3）进行转化，并引入伴随实际问题的约束条件，通过最小化f 实现求解，如式（4）所示：

式中：S、W为权重矩阵。S决定更看重实际控制器中的哪一项；W用来限制求解结果大小。关于xTWx，由齐次线性方程组式（5）转化得到。可以看出，在需要同时满足式（3）和式（5）的情况下，二次规划不能完全采用最小解作为分配结果，并且由于权重的固定，分配结果会存在偏见。

一方面，严格把关学业指导专业老师，能够保证学业指导专业教师队伍质量，另一方面，加强评价体系和考核制度，也能够增强学业指导专业教师的责任心和使命感。同时有利于及时发现学业指导过程中存在的问题，并有针对性的提出合理的对策和建议。从而有效促进提高教育质量和人才培养质量。

2 力系简化神经网络

力系简化神经网络是结合自编码器结构与空间力系简化原理的神经网络结构。

2.1 自编码器结构

自编码器是一种自监督学习方法，能够从无标签样本中学习样本数据特征[15]。其功能是通过编码层将输入数据重建为低维度数据，该低维数据可通过解码层还原重构。当损失值降低到满足任务要求时，就可以认为特征输出即为原始数据在低维空间下的特征[16]。

2.2 力系简化神经网络结构

空间任意力系简化是基于力的平移定理，将复杂的空间任意力系转化为空间汇交力系和空间力偶系2 个简单力系[17]，该过程是对力系的还原重构。

对自编码器结构做如下改进：用空间任意力系简化过程代替传统自编码器的解码网络，如图1 所示。基于该结构训练神经网络，当损失值接近于0时，编码层神经网络即为力系的分配过程，且满足力系等效原则。

图1 自编码器改进结构Fig.1 Improved autoencoder architecture

2.3 数据集和训练流程

实现动态控制需要能够在任意姿态下完成控制分配。因此，输入数据集S包含两类信息：目标控制量和姿态四元素Q，如式（6）～式（8）所示：

另外，对任意姿态进行拟合，就存在无限数据集，设计内外双循环训练流程，如图2 所示。

图2 内外双循环训练流程Fig.2 Inner and outer double loop training flow chart

在训练时，采用均匀分布随机生成n 组向量S1作为内循环样本数据，当达到设定训练次数之后，跳出内循环，然后重新生成n 组向量S2，再进入内循环进行训练。其中S1与S2相互独立。

3 实验与分析

3.1 神经网络训练实验

根据形状特点，损失函数分为固定斜率和变化斜率。固定斜率以平均绝对值误差损失函数L1（Mean Absolute Deviation）为代表；变化斜率以平均平方损失函数L2（Mean Square Error）为代表[18]。学习率更新方法分为固定学习率和动态学习率，采用Adam[19]优化器的动态学习率作为对照，lr 为当前训练步的学习率。如式（9）～式（11）所示。其余参数如表1 所示。

表1 训练实验参数Tab.1 Training experimental parameters

组合成4 种不同的实验条件：①L1与固定学习率；②L1与优化器Adam 的动态学习率；③L2与固定学习率；④L2与优化器Adam 的动态学习率。

在（ABCD）4 种不同的实验条件下，完成神经网络训练，结果如图3 所示。可以看出，条件B 有更好的收敛效果，而且更稳定。

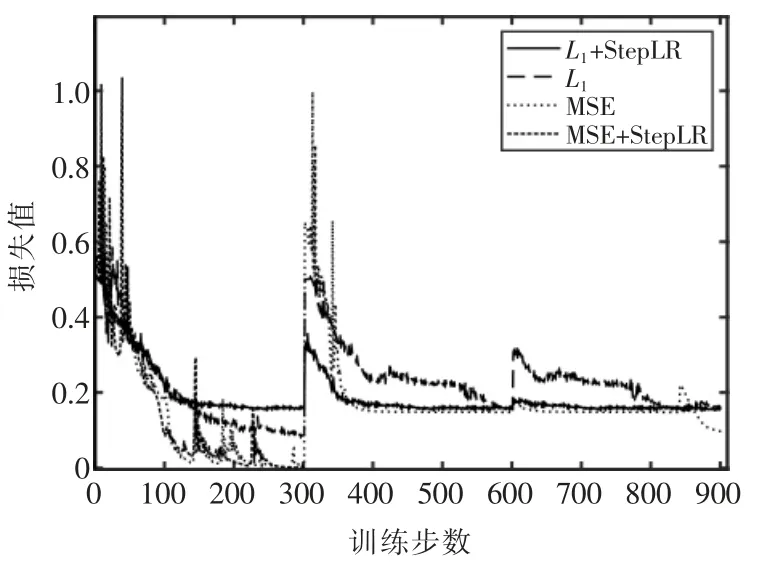
图3 训练实验对比Fig.3 Comparison of training experiments

条件B 下的训练结果，如图4 所示。标出了在外循环初始时刻的损失值。随着训练推移，外循环初始损失值在不断减小，表明神经网络在逐渐拟合未曾送入过的数据集，证明了训练方法可以解决无限数据集问题，适用于控制分配。

图4 条件B 训练结果Fig.4 Condition B training results

3.2 单刚体控制问题

针对冗余控制分配，将问题简化为单刚体控制问题进行讨论，如图5 所示。假设存在一个长方体刚性构件和4 个外力，这4 个力作用于单刚体上的不同点，作用点如表2 所示。刚体的所有运动，包括克服重力，都由这4 个力来完成。该刚体的动力学参数如表3 所示。表2 和表3 中数据的参考坐标系均为图5 中坐标系o，该坐标系原点位于质心，随刚体运动。

表2 力的作用点Tab.2 Point of force application

表3 刚体动力学参数Tab.3 Rigid body dynamics parameters

图5 单刚体受力示意图Fig.5 Force on a single rigid body

控制该刚体时，先根据目标位置与当前位置关系计算出虚拟质心力系U，如式（12）所示。然后将该虚拟质心力系分配为4 个实际控制力F1、F2、F3、F4，分配关系如式（13）所示：

式中：E为单位矩阵；pi为力作用点相对质心坐标系o 的位置向量；[pi]x为pi的反对称矩阵。每个实际力有3 个分量，则向量x共12 维。因此可知矩阵D为行满秩矩阵，所以单刚体控制问题属于过驱动系统。

3.3 单刚体悬浮控制实验

该实验控制目标是利用4 个外力去平衡重力，使单刚体保持在离地面0.2 m 处悬浮。

悬浮开始到稳定的总用力如图6 所示。使用神经网络得到的分配方案相比二次规划能够将总用力从47 N 减少到44.8 N，更接近刚体重力，说明神经网络方法能有效减少无用功。

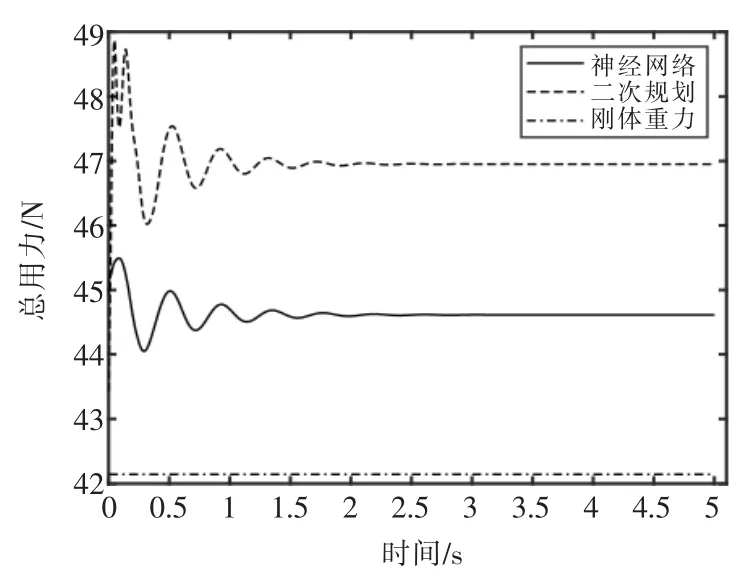
图6 总用力对比图Fig.6 Total force comparison chart

神经网络和二次规划在该实验下的分配结果，如图7 所示。图中的点划线为0.25 倍单刚体重力。神经网络相比二次规划，得到的结果更接近平均值，且分布更集中，说明神经网络能避免人为设置权重引入的偏见。

图7 分配结果对比Fig.7 Comparison of allocation results

3.4 单刚体轨迹跟随控制实验

该实验控制目标是利用4 个外力控制单刚体在1 倍重力环境下，维持高度为0.2 m 的同时，由静止开始跟随一条圆形轨迹，轨迹方程为

整个跟随过程中的总用力如图8 所示。神经网络相比二次规划能够将总用力从47 N 减少到45 N，说明神经网络在动态控制时，也能得到更小的分配方案。该实验的轨迹跟踪情况如图9 所示，放大了起始阶段（右上角）和终止阶段（右下角）。在起始阶段，神经网络的跟踪轨迹偏离目标轨迹更小；在终止稳定阶段，神经网络的稳态误差也更小。说明在动态控制任务中，神经网络同样具有优势。

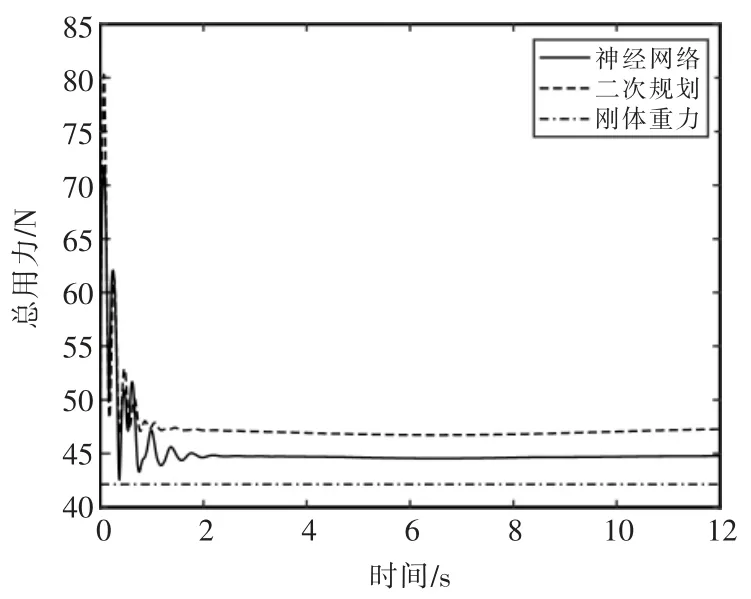
图8 轨迹跟踪所用外力总量Fig.8 Total force used for trajectory tracking

图9 轨迹跟踪情况Fig.9 Trajectory tracking situation

4 结语

结合自编码器结构和空间任意力系简化原理，提出了一种力系简化神经网络结构，并证明该结构可以训练神经网络实现控制分配。针对神经网络的训练，提出了合适的数据集和训练流程，并通过实验证明，力系简化神经网络结构能有效训练神经网络用于控制分配。

悬浮控制实验和轨迹跟随控制实验的结果表明，神经网络相比二次规划，分配方案分布更集中，不存在偏见问题。同时，神经网络使用的总用力约为44.5 N，二次规划约为47 N，而单刚体总重力为42.14 N，说明神经网络方法能减少驱动器所做的无用功。

本文方法的优点是仅需要确定被控系统的力系简化过程，即可训练神经网络实现控制分配。对于异形结构、变结构或具有复杂耦合情况的控制系统，得到力系的简化过程比分解过程更容易，这证明力系简化神经网络结构可以是异形结构、变结构或者复杂耦合控制系统的控制分配解决方案，这将是更深入探究应用的方向。