防洪坝潜跃条件下地埋式消力池水力设计

葛庆斌

(费县水利工程保障中心,山东 临沂 273400)

0 引 言

消力池是位于大坝底部出水口、斜槽和涵洞下方的水工结构[1-2]。这种结构的主要目的是消散流出的多余能量,以减少河流系统中出现不良冲刷的风险。以往关于地下消力池中的水跃研究可分为3大类:仅在水槽宽度突然增大时的水跃;仅在河床处突然下降;以及突然膨胀和突然下降的组合。而对突扩突降水跃的研究大多是通过调节尾水位进行的,但与实际情况相差甚远;在目前的研究中,没有对尾水进行控制,水跃是由端槛强制的,与实际情况类似。但仍解决受限复杂结构内的强制水跃问题[3-5]。

本研究通过实验研究了消力池中强制水跃的水力特性,并尝试在不同的水力和几何条件下对其可能的流动模式进行分类。利用实验结果,提出了一种基于消力池下游水流要求的消力池内强制淹没水跃的设计方法。

1 材料与方法

1.1 实验装置

文章构建的模型是由一个宽0.5m、深0.5 m、长9 m的水平矩形水槽组成。在整个模型中,使用离心泵支持循环水系统。上游供水箱配备了一个校准的90°V形切口堰。采用点规测量了V形槽堰上方的水头,然后使用平均时间体积法得到水头与相应流量之间的关系。在主蓄水池内部安装了两个穿孔板,以实现底部出口的层流流出流量;因此,厚度等于底部出口的均匀超临界流最终进入消力池[6]。模型设置的侧面和平面示意图,如图1所示。

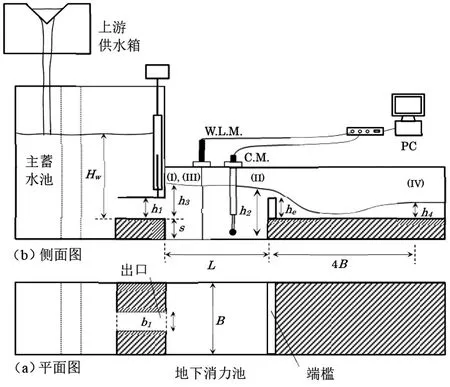
图1 模型设置的侧面和平面示意图

1.2 实验测量

所有实验的基本数据收集过程都是相同的。从消力池的侧面和平面视图拍摄数码照片,并使用高分辨率数码相机记录视觉观察。使用水位计测量整个消力池的水深及其波动,水位计的采样频率设置为50 Hz。使用电磁流量计在不同的横截面和纵截面上测量速度的三维分量。在每个截面上以2.5 cm间隔测量流速。

2.3 实验条件

实验采用了不同的消力池几何形状:消力池长度(L=75、100和125 cm)、跌落高度(s=5、10和15 cm),所有实验的消力池宽度相同,即为水槽宽度B=50 cm。对于不同的消力池几何构型,系统地检查了不同高度(he=0、4、8、12和13.5 cm)的端槛几何构型,以获得最佳情况。端槛垂直放置在正台阶上方,并垂直于水槽的纵轴。除了底部出口处3种不同的超临界流弗劳德数(即Fr1=2.8、4.9和5.1),只检查了底部出口的一个维度(h1=5cm和b1=10 cm),因此,得到了k=0.2(k=b1/B)的膨胀比,与防洪坝的平均实际膨胀比相似。表1显示了本研究中考虑的实验条件。

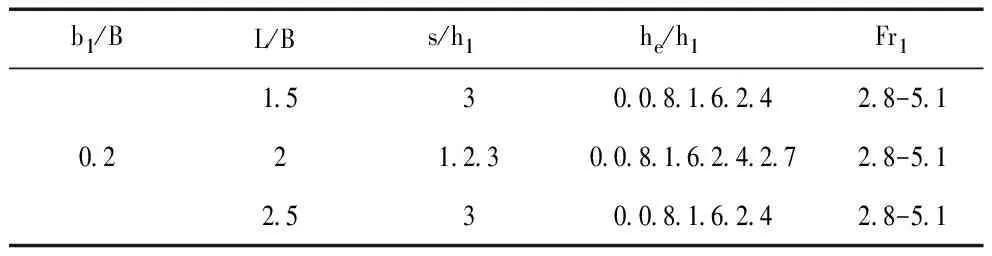
表1 实验条件

2 结果与讨论

2.1 地下消力池的消能效果

根据不同的归一化参数绘制归一化速度降低图,以便更好地了解其对消力池内消散机制的影响。当Fr=2.8-5.1和s/h1=3时,消力池内的归一化速度降低与L/B的周期性和稳定水跃见图2。

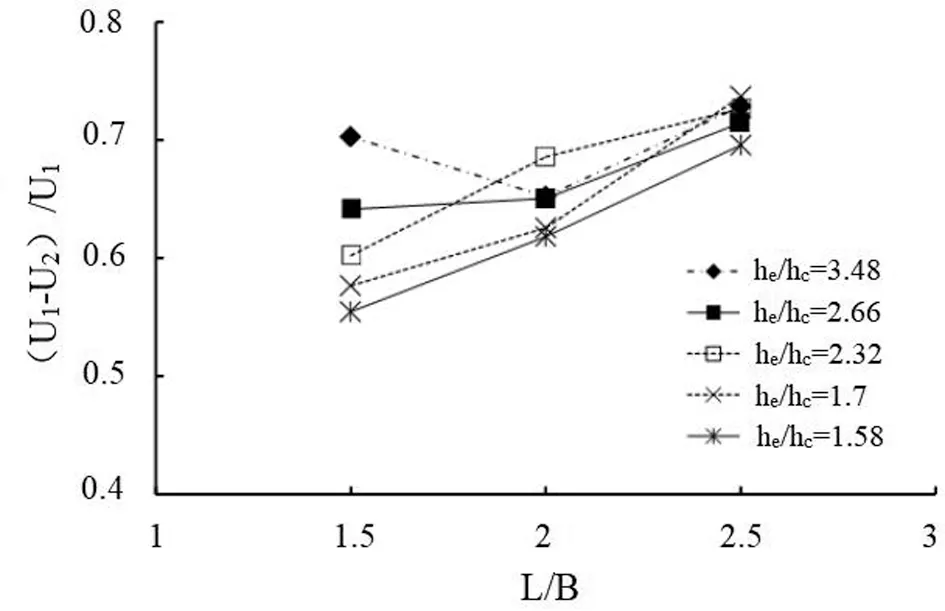
图2 消力池内的归一化速度降低与L/B的周期性和稳定水跃

图2显示了作为归一化消力池长度(L/B)的函数,截面I和II之间的归一化速度降低U1-U2/U1。U1是初始出口速度,U2是端槛上游的最大速度。在短消力池情况下(L/B=1.5),端槛高度的变化会导致归一化速度降低发生很大变化,然而,对于长消力池(L/B=2,3),端槛高度的变化会导致归一化速度降低发生微小的变化。结果表明,与较长的消力池相比,较短的消力池中归一化速度降低更多地取决于归一化端槛高度he/hc。总体趋势表明,增加归一化消力池长度会增加速度降低的幅度。

2.2 地下消力池设计步骤

2.2.1 确定连续深度

综上所述,考虑消力池的中等端槛和落差可以有效地降低流速。此外,这种端槛和落差的组合产生了稳定淹没流。因此,仅针对稳定淹没流提出设计准则。

为了计算强制淹没水跃的连续深度h2,在忽略河床剪应力的情况下,截面I和II之间应用动量方程公式为:

(1)

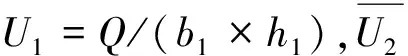
Y23-(Y32+2Y3S+S2+2Fr12k)Y2+2Fr12k2=0

(2)

式中:Y2为归一化序列深度,Y2=h2/h1,S为跌落数,S=s/h1,k为膨胀比,k=b1/B。

2.2.2 确定端槛高度

在水平轴上选择端槛下游的期望弗劳德数(Fr4),再在垂直轴上找到相应的he/h4值。消力池下游h4处的水深可根据选定的Fr4和设计流量计算。端槛上的能量可使用临界深度(hc)和端槛高度(he)来计算。若假设在端槛上自由落体流没有能量损失,则消力池下游的能量等于端槛顶部的能量,如下式所示:

(3)

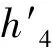
2.2.3 确定消力池长度

正确估计消力池长度(L)和端槛位置是至关重要的。如果端槛距离出口太近,则没有足够的空间来诱发水跃。消力池长度(L)可使用等式4获得。

(4)

式中:HL为由于水跃引起的水头损失;H1为落差面处的总水头,可定义为:

(5)

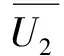
2.2.4 确定跌落高度

可使用图3中的稳定水跃数据找到下落高度s。hc、L、B和he的已知值及与稳定水跃数据拟合的线性方程可提供用于设计步骤的落差高度适当估计。

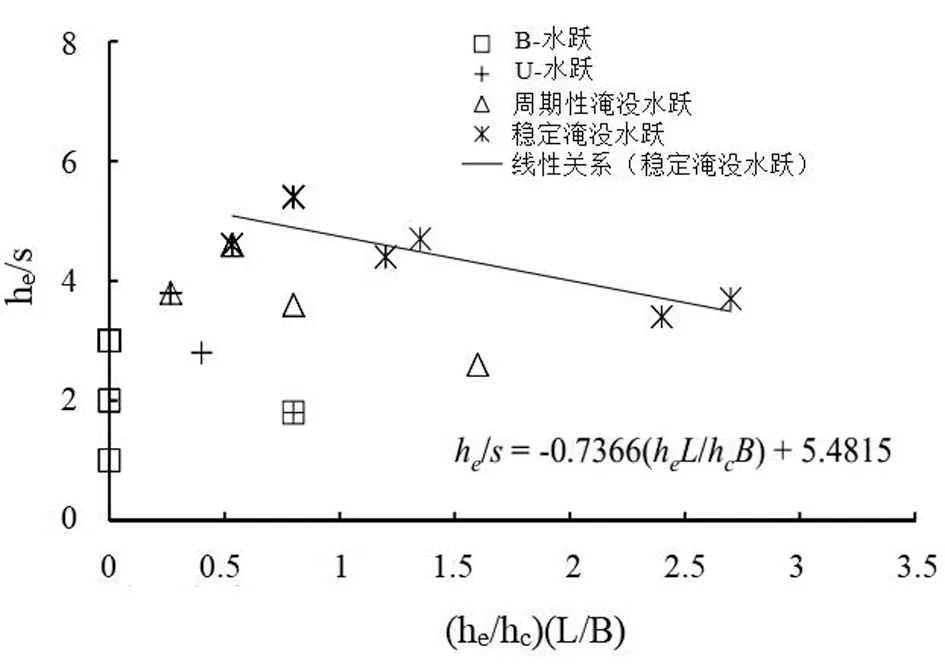
图3 消力池几何参数和水跃类型

2.2.5 消力池的拟议设计步骤

对于上游端为负台阶、下游端为端槛的消力池水平护坦,可提出以下设计步骤:

1)给定上游边界条件,包括设计流量Q、底部出口尺寸b1和h1、接近弗劳德数Fr1和河道宽度B。

2)使用上游边界条件计算临界深度hc。

3)考虑到稳定的淹没水跃,选择合适的he和L,然后选择s。

4)在假设没有能量的情况下,检查从端槛下游获得的水深h4和下游弗劳德数Fr4。如有必要,可通过考虑端槛上自由落体流的能量损失,使用计算修改后的h4。

5)重复步骤2～3,直到下游条件达到可接受水平。

3 结 论

文章研究了地下消力池(消力池)内的强制水跃。消力池内观察到的流型分为五大类,其主要控制参数为端槛高度he和消力池长度L,而Fr1的变化对消力池内的流型和能量损失函数没有显著影响。并得出以下结论:

1)中等消力池长度与中等端槛高度(1.6

2)由于端槛上的自由落体流,高端槛可能会对下游速度产生负面加速。

3)消力池的中等深度对速度降低有积极影响,但进一步增加深度则对速度降低和设计成本均无好处。最佳跌落数会因弗劳德数的不同而不同,一般来说,弗劳德数越高,消力池越深。