富水砂层输水隧洞隔水层厚度的影响因素与分析
张迪
(朝阳县水务局,辽宁 朝阳 122000)
0 引言
我国的水资源总量十分丰富,但时空分布不均,造成诸多水资源供需矛盾,给经济社会的可持续发展带来许多困扰。针对这一问题,积极进行水利工程建设,实现跨流域调水无疑是当前最为有效的措施。在长距离调水工程建设中,输水隧洞往往是不可避免的工程手段,而其在施工建设和其他方面也面临着更加严峻的挑战,特别是在建设过程中经常面临穿越软弱地层、富水地层及流沙层等复杂的工程地质条件[1]。当输水隧洞穿越富水地层时,施工开挖极易出现塌方、突水涌沙及地表沉降等工程事故,进而严重影响施工建设的安全进行[2]。因此,针对复杂地质条件下输水隧洞施工优化设计具有十分重要的意义和作用。
辽宁省某“十四五”重点输水工程输水隧洞一标段的K2+454~K2+778 洞段处于河谷地段,部分区间穿越富水砂层。根据前期的地质勘查资料,该洞段的第四系富水砂层厚度为2.23~12.67 m,给围岩和衬砌结构的稳定性带来诸多挑战。在工程施工建设过程中,如果不能保证隧道拱顶和富水砂层之间的隔水层有足够的厚度,就难以保证施工的安全[3]。基于此,此次研究利用数值模拟的方式,对富水砂层输水隧洞隔水层厚度的影响因素展开分析,以便为相关的理论研究和工程建设提供有益的支持和借鉴。
1 FLAC3D 有限元模型
1.1 计算模型的构建
FLAC 是美国INASCA 公司在有限差分法基础上开发的一款针对连续介质的力学仿真软件。FLAC3D 作为三维差分程序,是二维程序的升级版本,该软件采用显式拉格朗日算法和混合-离散分区技术,可以实现对岩土体结构受力特征的准确模拟[4],该软件还有一个显著优势就是计算过程中不需要形成刚度矩阵,占用的资源量较小。基于此,此次研究采用FLAC3D 有限元软件进行计算模型的构建。
在模型的构建过程中,考虑到流固耦合的边界效应对计算结果的影响,模型的左右两侧及下边界取隧洞开挖断面直径的5 倍,上边界取到地表。几何模型以隧洞开挖方向为X轴的正方向,以垂直于X轴指向右侧的方向为Y轴的正方向,以竖直向上的方向为Z轴的正方向。输水隧洞采用全断面开挖方式,开挖进尺为2.00 m,在开挖之后立即进行喷射混凝土支护[5]。计算模型的围岩选择摩尔-库伦本构模型,衬砌结构总厚度为80 cm。初期支护体系采用壳单元模拟,围岩和衬砌混凝土采用实体单元模拟。
1.2 边界条件和模型参数
根据研究对象的实际特点,对模型的两侧施加竖向位移约束;模型的底部施加全位移约束;模型的上表面为自由边界条件,不施加位移约束。在模型的流固耦合计算过程中,将模型的侧面视为不透水边界条件,模型的底部为透水边界条件,将地表的静水压力设置为0[6]。在隧洞开挖之后,开挖边界以外设置为透水边界条件,初支完成之后的支护段设置为不透水边界,初始渗流场随水力梯度呈线性增长。
数值模拟过程中,选择科学合理的模型物理力学参数极为重要,会对计算结果产生直接影响。此次研究过程中结合相关施工规范和背景工程的地质资料,确定如表1 所示的模型材料物理力学参数。

表1 模型材料物理力学参数
1.3 隔水层厚度
在穿越富水沙地层的地下洞室工程施工过程中,隧洞的主体结构和富水沙层之间必须要有一定厚度的隔水层。因此,如何确定安全的隔水层厚度就成为此类工程研究的重要课题[7]。目前,针对地下洞室工程隔水层厚度的计算方法主要是极限分析法、极限平衡法、滑移线法、积极条分法。此次研究中借鉴王洪涛的相关研究成果[8],利用极限分析法对安全隔水层厚度进行预测,在计算过程中结合隧洞顶板的破裂特征,构造出隧洞上方土体极限状态下的破裂机制,并基于线性M-C 强度准则,利用计算分析上限定理对隔水层厚度进行求解。
1.4 计算方案
结合背景工程的实际情况,设置隧洞半径为2.0,2.5,3.0 m;隔水层岩土体的内摩擦角为21.0°,粘聚力为140 kPa,土体重度为24 kN/m3,隧洞埋深为15.0 m,支护力为0 kPa。研究中为了简化,计算过程中先保持其余参数不变,对一个参数在不同水平下的隔水层厚度进行计算,并对计算结果进行对比分析。
2 计算结果与分析
2.1 埋深
利用构建的有限元模型,在其余参数不变的情况下,对隧洞埋深分别为11.0,13.0,15.0,17.0,19.0 m 的安全隔水层厚度进行模拟计算。根据计算结果,绘制出安全隔水层厚度的变化曲线,如图1 所示。由图1 可以看出,在隧洞直径相同的情况下,安全隔水层的厚度随着隧洞埋深的增加呈现出逐渐增大的变化趋势,其增大特征为典型的线性特征。因此,穿越富水砂层输水隧洞的埋深越大,应该选择厚度更大的隔水层厚度。另一方面,隧洞半径也是安全隔水层厚度的重要影响因素,在埋深相同的条件下,安全隔水层的厚度与隧洞半径之间也存在比较明显的正相关关系。
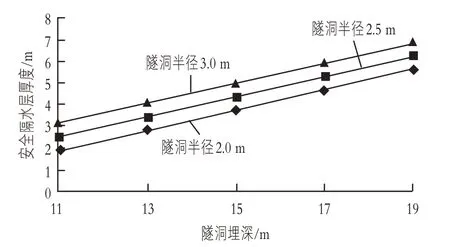
图1 安全隔水层厚度随隧洞埋深变化曲线
2.2 土体强度参数
研究中保持其余参数不变,分别对隔水层岩土体粘聚力为120,130,140,150,160 kPa;隔水层内摩擦角为17°,19°,21°,23°,25°;隔水层岩土体重度为20,22,24,26,28 kN/m3的安全隔水层厚度进行模拟计算。根据计算结果,绘制出安全隔水层厚度随粘聚力、内摩擦角及重度的变化曲线,分别如图2—4所示。由图2—4可以看出,随着粘聚力、内摩擦角和重度的增大,安全隔水层的厚度呈现出不断减小的变化特征,减小的速率也不断变小。
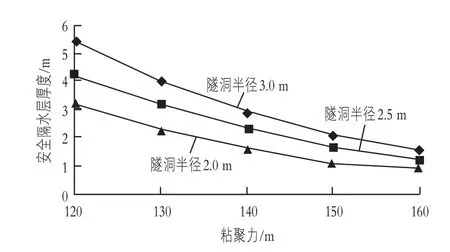
图2 安全隔水层厚度随粘聚力变化曲线
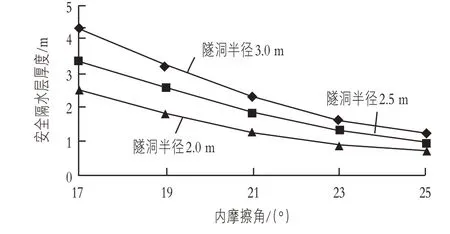
图3 安全隔水层厚度随内摩擦角变化曲线

图4 安全隔水层厚度随重度变化曲线
2.3 支护力
在保持其他参数不变的情况下,对支护力为0,40,80,120,160 kPa 的安全隔水层厚度进行模拟计算。根据计算结果,绘制出安全隔水层厚度随支护力的变化曲线,如图5 所示。由图5 可以看出,随着支护力的不断增大,安全隔水层的厚度呈现出不断减小的变化特点,且减小的速率不断增大。由此可见,输水隧洞的初期支护和二次衬砌结构对提升围岩的安全性和稳定性具有十分重要的意义和作用。
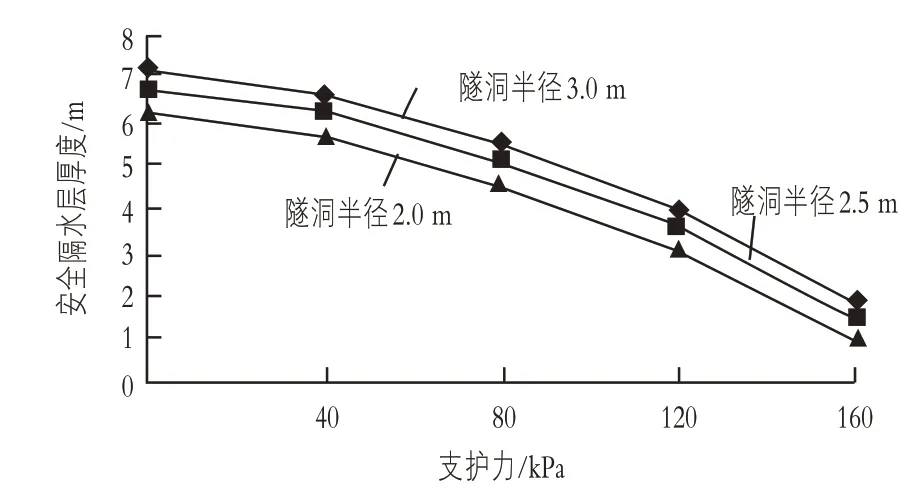
图5 安全隔水层厚度随支护力变化曲线
3 结语
此次研究利用数值模拟的方式探讨了富水砂层输水隧洞隔水层厚度的影响因素,并获得相应的变化规律。根据计算结果,提出如下工程建议:在输水隧洞选线过程中,应该尽量避开富水沙层,如无法避开时,应该尽量增加隔水层的厚度,以提高隧洞施工和运行安全;在富水沙地层输水隧洞开挖施工过程中,应该注意及时支护和选择科学合理的支出参数,保证拱顶围岩的稳定性;鉴于安全隔水层岩土体参数对安全隔水层厚度存在显著影响,在实际工程施工过程中,可以通过超前小导管注浆等工程技术措施提高隔水层的强度参数。

