悬链线钢管混凝土单管拱破坏试验研究

刘增武 ，王邵锐，辛景舟，周建庭 ，李英斌

(1.重庆交通大学 土木工程学院，重庆 400074；2.重庆交通大学 山区桥梁及隧道工程国家重点实验室，重庆 400074)

在多山区的中国，混凝土拱桥因其刚度大、承载性能高、抗震性能好和造价低等优点，成为桥梁建设的排头兵，在公路、铁路和城市桥梁中均有广泛应用。钢管混凝土拱按拱轴线形状主要分为圆弧拱、抛物线拱，以及悬链线拱等。根据相关文献[1-2]，我国钢管混凝土拱桥广泛采用悬链线拱，尤其是上承式拱桥和中承式拱桥，悬链线拱占所有拱轴线形式的43%。目前，国内外已有较多学者对钢管混凝土拱展开了力学性能试验和理论研究，WU 等[3]研究了抛物线无铰拱在均匀轴压作用下的稳定性，分析了矢跨比和长细比对屈曲荷载的影响，并提出了预测其极限承载力的方法。PI 等[4]研究了钢管混凝土圆弧拱的面内屈曲稳定性行为，获取了平面内强度设计方法。陈宝春等[5]开展了钢管混凝土拱的面内承载力试验研究，得到了钢管混凝土拱的破坏模式和极限承载力计算方法，并开展了参数分析。LIU等[6-7]为确定钢管混凝土拱平面内屈曲承载力，研究了矢跨比对桁架拱承载力的影响，并基于有限元结果提出了均布荷载下钢管混凝土拱的设计公式。陈爱国等[8]采用二阶弹塑性有限元法对圆形截面两铰抛物线钢管拱的平面内稳定承载力进行了研究，得出了矢跨比和长细比是影响钢管拱承载力的重要因素。HU 等[9]为研究抛物线无铰拱平面内稳定性，开展了跨度相同但矢跨比不同钢管混凝土拱破坏试验，得出了随着矢跨比降低承载力降低，以及荷载达到承载力80%后，钢管对核心混凝土产生约束效应的结论。殷海棠[10]开展了抛物线形单圆管混凝土拱稳定承载力试验，探讨了拱顶加载和半跨加载下拱的破坏模式和受力行为，并做了承载力影响参数分析。YUAN等[11]研究了均布荷载作用下抛物线钢管混凝土拱的承载力，并基于稳定理论，考虑矢跨比的影响对稳定性方程展开研究。GENG等[12-13]采用ABAQUS 的有限元方法，研究了混凝土时变效应对抛物线单钢管混凝土稳定承载力的影响，并用试验拱的承载力试验数据验证分析方法的正确性。PI等[14]采用虚功法对浅钢管混凝土拱的长期非线性弹性面内行为和屈曲进行了理论分析。YANG 等[15]介绍了线弹性迭代技术对钢管混凝土拱进行塑性极限分析。然而，以上研究中钢管拱的形式均为圆弧拱或者抛物线拱，圆弧拱和抛物线拱与悬链线拱的拱轴线形式区别较大，以及拱轴线方程形式和参数有本质区别，这可能导致拱肋的受力状态也存在差别。目前，虽然悬链线钢管拱被大量用于工程，但是在力学试验和相关理论研究尚不足。另外，相比于圆弧拱和抛物线拱，在试验研究时，悬链线拱的制作难度更大。因此，开展悬链线钢管混凝土拱承载力试验和力学性能研究具有重要的意义，为工程设计提供指导，也为后续的理论研究铺垫基础。鉴于此，本文依托净跨径95 m 的单管混凝土拱桥—瓦石窝大桥，开展1∶16 的缩尺模型试验，对悬链线钢管混凝土拱开展力学性能试验研究。分别开展拱顶和1/4 处加载试验，研究不同单点加载方式下拱的面内破坏模式和受力特点。接着采用数值分析方法进行参数扩展分析，开展不同加载方式、拱轴系数、矢跨比、含钢率等参数对钢管混凝土悬链线拱承载力的影响，为增补钢管混凝土拱承载力试验库和为工程设计提供借鉴，同时也为悬链线钢管混凝土拱的理论计算铺垫基础。

1 试验概况

1.1 试件设计

以目前国内最大跨径的单管钢管混凝土拱桥-瓦石窝大桥为依托，开展缩尺模型试验研究。瓦石窝大桥为下承式悬链线钢管混凝土拱桥，主拱净跨径为95 m，净矢跨比为1/3.5，拱轴系数为1.5；主拱钢材采用Q355，管内混凝土采用C60；钢管外径为1.55 m，壁厚为26 mm。瓦石窝大桥立面图如图1所示。

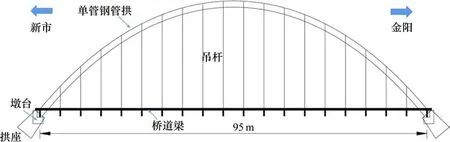
图1 瓦石窝大桥立面图Fig.1 Elevation of Washiwo Bridge

对瓦石窝大桥主拱进行1∶16 缩尺，设计并制作了2 个钢管混凝土试验拱，加载工况为单点加载，分别为拱顶加载(A-1)和1/4(A-2)加载。试验拱和实桥主拱尺寸信息见表1。

表1 试验拱和实桥主拱信息Table 1 Information of test arch and main arch of real bridge m

由于钢管外径0.096 9 m，壁厚0.001 63 m 的Q355 号钢材较难购买，试验拱实际钢材采用Q345，钢管外径为0.089 m，壁厚为4 mm，由成品无缝钢管煨弯而成；管内混凝土采用C60。拱轴系数与实桥保持一致，仍为1.5。试验拱尺寸及截面见图2。

图2 试验拱尺寸图Fig.2 Dimension diagram of test arch

1.2 试验装置

图3展示了试验拱的加载和限位装置，试验系统由拱座反力架装置、千斤顶配套加载装置、拱肋横向限位装置以及包含拱座的试验拱组成。其中拱座反力架装置包括反力架、固定反力架的锚杆。反力架限制拱座在试验拱加载全过程的滑动，实验前要做预压。拱肋加载装置由千斤顶、压力传感器、加载板和配套工装组成，加载时要保证压力传感器、千斤顶、加载板，以及拱肋加载垫块在竖直直线上。拱肋横向限位装置由限位横梁、限位板，以及固定螺栓组成，可通过滑槽来调整限位板位置，保证试验拱在加载过程中不出现平面外变形，并在拱和限位板之间粘贴四氟板来减小加载后期接触后的摩擦。

图3 加载和限位装置Fig.3 Diagram of loading and limiting device

1.3 材料力学性能

实验前对试验拱的钢管和管内混凝土材料性能进行了测试，根据金属材料拉伸试验规程[16](GB/T 228.1—2010)对钢管力学性能进行测试，测得钢管的屈服强度361 MPa，抗拉强度为540 MPa，弹性模量为210 GPa。按照混凝土物理力学性能试验方法标准和相关文献[17-18]进行了混凝土试块的轴压试验，混凝土立方体抗压强度、棱柱体轴心抗压强度和弹性模量分别为51.85 MPa，32.4 MPa 和34.84 GPa。

1.4 试验测试内容及加载程序

测试试验拱在加载过程中的位移和应变，选取的关键截面为L/8，2L/8，3L/8，4L/8，5L/8，6L/8 和7L/8 处布置水平和竖向位移计来测试拱的位移，同时在拱座布置了水平、竖向和面外的位移计，拱A-1 和A-2 位移计布置如图4 所示。为了分析拱的破坏模式和钢管对核心混凝土的套箍效应，在试验拱两侧拱脚和8个关键断面布置了轴向和环向应变片，每个断面轴向应变片布置4个，环向应变片布置2个，分别位于钢管顶部和底部。由于在加载处钢管上表面存在加载块，因此，加载处的应变片位置偏离加载点60 mm。应变片布置如图5所示。

图4 位移计布置Fig.4 Layout of displacement meter

图5 应变片布置Fig.5 Layout of strain gauge

为了保证钢管混凝土拱试验数据在试验全过程中的准确性，试验前进行预加载试验。通过预加载可消除试验装置的非弹性变形，以及检查加载装置、位移计和应变片等是否正常，结构是否有效传力。预加载荷载由试验前计算确定，不超过极限荷载的30%。正式加载采用多次分级加载，分级荷载为5 kN。为确保拱在每级荷载下试验拱变形充分，每级荷载持荷2 min；当试验拱加载处钢管变形增加较快时将分级荷载减小，或采用缓慢连续加载。当试验拱变形持续增加且千斤顶油压表读数下降时，这时停止加载。

1.5 初始缺陷

试验拱的线形受到钢管煨弯、运输、安装，以及焊接等因素的影响，因此试验拱的实际拱轴线形会存在几何缺陷。通过全站仪测量试验拱的初始缺陷，见图6。首先，在钢管表面沿着拱轴线粘贴反射片，应保证反射片位于拱截面中心处。然后通过全站仪对各个测点进行测量，测量时须预先确定好基准测点。最后试验拱的初始缺陷值可通过各测点的实测坐标与理想的设计坐标推算得出。试验拱 A-1 和A-2 的初始缺陷值如表2 所示，表中数值为各测点实际纵坐标与理想的设计纵坐标的差值，高为正，低为负。

表2 试验拱初始缺陷值Table 2 Initial defect value of test arch mm

图6 试验拱初始缺陷测量Fig.6 Initial defect measurement of test arch

试验拱A-1和A-2的拱轴线长度均为7 073 mm，A-1 和A-2 初始缺陷与拱轴线的长度比值分别为0.005 5和0.004 4。

2 试验结果及其分析

2.1 试验现象及破坏模式

试验拱拱脚的位移可以通过拱座来反映，在承载能力极限状态下拱脚的横向、水平和竖向位移见表3 所示。试验拱A-1 和A-2 拱脚最大水平位移和竖向位移分别为1.213 mm 和1.887 mm，拱座面内位移较小，并且拱脚处焊缝未开裂，表明拱座实现了无铰拱试验的目的。另外，各试验拱的横向位移均小于1 mm，拱面外变形可忽略，因此本次试验可视为面内破坏。

表3 试验拱位移Table 3 Displacement of test arch mm

各试验拱在不同加载力作用下竖向位移沿跨径的分布形态和变化规律见图7。由图7(a)可知，试验拱A-1的竖向位移在加载全过程中变化先慢后快，弹性阶段变化缓慢而进入塑性阶段后变化增快；试验拱最大位移位于拱顶截面处，左右半拱四分点处位移与拱顶截面相反，由于几何缺陷，左右半拱上拱的程度不同，拱肋变形不完全对称，试验拱整体破坏形态见图8(a)。由图7(b)可知，试验拱A-2 的左右半拱在弹性阶段竖向位移方向相反，但数值大小接近，随着材料进入塑性后，L/4加载处截面位移增长迅速，数值远大于3L/4 截面的位移值，拱肋变形为反对称，试验拱整体破坏形态见图8(b)。另外，比较图7(a)和7(b)可知，与拱顶加载相比，L/4 加载工况下的拱下挠值大，说明L/4加载工况为不利加载工况。

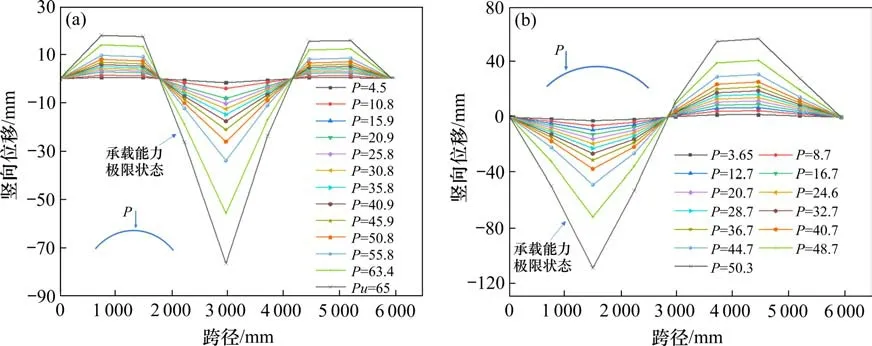
图7 试验拱竖向位移变化Fig.7 Vertical displacement change diagram of test arch

图8 试验拱整体破坏模式对比Fig.8 Comparison of overall failure modes of test arch

试验拱在承载力极限状态下的局部破坏形态如图9所示。试验拱的钢管在加载处发生了明显变形，其他位置的钢管均未出现明显的变形。试验拱A-1在加载处出现肉眼可见钢管变形，但是未发生屈曲、褶皱现象，这说明钢管和混凝土协同工作性能好，钢管环向约束效应充分发挥。打开钢管后，加载处截面的混凝土下缘出现多条竖向裂缝，表明加载处截面下缘存在较大的拉力，使得该截面形成塑性铰。另外，在两侧拱脚和L/4 处的混凝土也出现竖向裂缝，说明这些位置处混凝土也因拉应力过大而开裂形成了塑性铰，破坏模式为四铰破坏。试验拱A-2的钢管在加载处也出现了较大变形，局部仍然没有发生屈曲、褶皱现象。打开钢管后，在加载点左侧出现较明显的混凝土竖向裂缝，除此之外，在两侧拱脚，以及3L/4 处也出现了混凝土竖向裂缝，破坏模式也为四铰破坏。

图9 试验拱局部破坏形态Fig.9 Local failure mode of test arch

2.2 试验拱荷载-位移曲线

悬链线钢管混凝土试验拱在加载全过程下的荷载-位移曲线如图10所示，图中Pu为试验拱极限承载力。由图中荷载-位移曲线变化规律可知，试验拱的破坏过程主要分为弹性、弹塑性，以及失稳破坏3个典型阶段。在加载前期，随着荷载的增加，各个测点的竖向位移呈现线性变化；当荷载达到0.6Pu时，试验拱进入弹塑性阶段，随着荷载增加位移变化变现出非线性的特征；当荷载超过0.8Pu时，竖向位移增加迅速，非线性特征更加明显，直到试验拱被压溃。通过图10(a)还可以得知，试验拱A-1 左右半拱对称处测点的荷载-位移曲线变化规律一致且数值虽有偏差但吻合较好。从图10(a)和10(b)对比来看，拱顶加载极限荷载值要大于1/4 加载工况，说明不同加载方式对拱的承载能力有影响，为保证拱的安全，设计时应考虑偏载的影响。

图10 试验拱荷载-位移曲线Fig.10 Load displacement curve of test arch

2.3 试验拱截面应变分布

悬链线钢管混凝土拱在单点集中力作用下，拱主要产生轴力和弯矩，在轴力和弯矩作用下，钢管拱截面上下缘的轴向应变值差别较大且拉压状态不同。图11 为在承载能力极限状态钢管混凝土悬链线拱拱肋上表面和下表面各测点的轴向应变分布情况。从图11 可知，在承载能力极限状态时，试验拱A-1拱肋上、下表的轴向应变基本以正对称的形式分布，拱顶加载区域和两侧拱脚拱的上表面受压、下表面受拉，其他区域上表面受压、下表面受压；拱顶加载区域、两侧拱脚段，以及L/4 和3L/4 钢管发生了屈服；另外，拱肋同一截面处的上下缘测点轴向应变的差值可体现截面弯矩的大小，由图11(a)和11(b)综合对比来看，在拱顶荷载作用下，钢管混凝土拱肋截面均存在弯矩，且拱顶截面弯矩最大，为整个拱的控制截面。

图11 试验拱A-1极限状态应变分布Fig.11 Strain distribution in limit state of test arch A-1

从图12(a)和12(b)中的曲线可知，试验拱A-2在承载能力极限状态时，L/4 加载处钢管发生屈服，除加载点外，左侧拱脚、3L/4 钢管上、下缘，以及右侧拱脚上缘也发生了屈服。通过分析拱肋截面上下缘测点的轴向应变差值可知，L/4 加载处截面正弯矩最大，左侧拱脚负弯矩最大，两者为拱肋弯矩控制截面。但从图12(a)和12(b)综合来看，L/4加载处截面正负应变均最大，1/4加载处截面为控制截面。另外，L/4 加载工况下的拱肋应变值大于拱顶加载工况，说明L/4加载工况更不利。

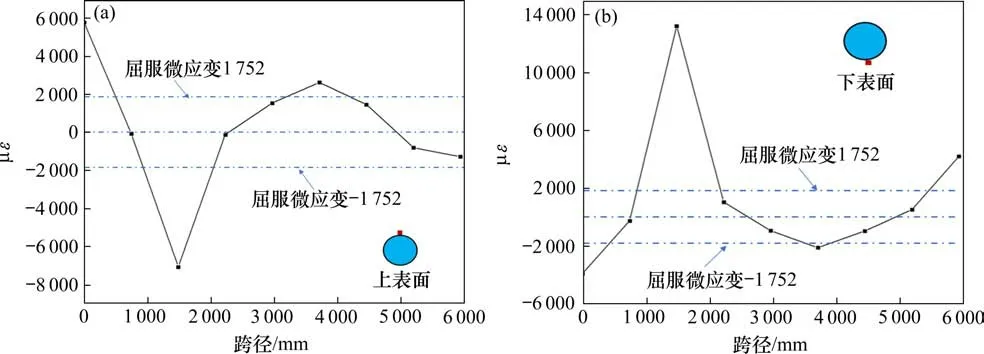
图12 试验拱A-2极限状态应变分布Fig.12 Strain distribution in limit state of test arch A-2

此外，对比图11 和12 可知，试验拱A-2 加载处截面下缘拉应变值大于试验拱A-1，此结果与图12试验拱A-2管内混凝土下缘裂缝宽度大于试验拱A-1的现象符合。

2.4 刚管对混凝土的约束效应

通过试验拱应变分布可知，加载处钢管的压应变最大，受力最为不利，为控制截面。因此可以通过分析控制截面处的轴向、环向应变来分析钢管的套箍效应。当钢管不对混凝土产生套箍效应时，该测点钢管的轴向应变εa和环向应变εc应该满足：εc=-μεa。如果存在套箍效应，那么混凝土膨胀使得钢管产生环向变形，这时钢管的轴向应变和环向应变应满足：εc＞-μεa。

图13 是试验拱A-1 拱顶截面上表面和试验拱A-2 1/4 加载处截面下表面测点的环向应变εc和μεa与荷载关系曲线。由图中曲线变化规律可以看出，加载前期试验拱的钢管环向应变εc曲线和-μεa曲线吻合较好，结果表明此时钢管未发挥套箍约束作用。当荷载达到约0.55Pu时，环向应变εc曲线比-μεa增长快，并且差别越来越大，这表明钢管对核心混凝土产生了套箍约束作用且套箍约束作用越来越强。图13(b))后期曲线差异不如a)明显与加载处钢管压力相对小，套箍作用相对小有关。另外，已有的抛物线拱钢管对混凝土的约束作用约在0.8Pu时出现[10]，与之相比，悬链线钢管混凝土拱的套箍约束效应发挥作用的时间更早。

图13 试验拱加载处应变与荷载关系Fig.13 Relationship between strain and load at the loading point of test arch

3 有限元模型与参数扩展分析

3.1 有限元模型的建立与验证

现有的梁单元模拟方法可以很好地预测钢管混凝土拱面内承载力[9]，利用Ansys 软件对试验拱进行数值分析，采用Beam188 梁单元分别模拟钢管和混凝土，沿着跨径方向划分为112个单元；两侧拱脚全部约束来模拟固结，见图14 所示。建模时，考虑实际的几何缺陷，不考虑拱脚焊接对结构的影响。钢管单元和混凝土单元共节点来保证两者协同工作。钢管本构采用理想弹塑性模型[19]，混凝土本构利用韩林海[20]提出的约束型混凝土模型，该本构关系考虑了钢管对管内混凝土的套箍约束效应。千斤顶单点加载力用节点荷载模拟。

图14 有限元模型Fig.14 Finite element model

图15 为试验拱A-1 和A-2 在拱顶和L/4 加载工况下的试验及有限元荷载-位移曲线对比，图 16为试验拱在承载力极限状态下竖向位移对比。试验拱A-1承载力试验值和有限元值分别为65.01 kN 和66.26 kN，差值百分比为-1.9%；试验拱A-2 承载力试验值和有限元值分别为50.27 kN 和50.93 kN，差值百分比为-1.3%。从图16中试验拱在极限荷载下的竖向位移的试验值和有限元值对比可知，有限元结果与试验结果吻合较好，且试验值略大于有限元值，这可能与试验拱拱脚无法保证完全固结、支撑拱座的反力架与地面存在微小滑移等有关。但从总体上来说，本文采用的有限元模拟方法可有效地对钢管混凝土拱承载力和变形进行模拟。保持跨径、矢高、钢管拱截面，以及材料不变，将试验拱拱轴线由悬链线变换为抛物线并用有限元法进行承载能力求解，得到抛物线拱在拱顶加载和L/4 加载下的承载力分别为58.8 kN 和46.7 kN，与悬链线钢管拱承载力相比，降低了11.2%和8.3%，承载力有一定程度的降低，见图17所示。

图15 荷载-位移曲线对比Fig.15 Comparison of load displacement curves

图16 极限状态竖向位移对比Fig.16 Comparison of vertical displacement in limit state

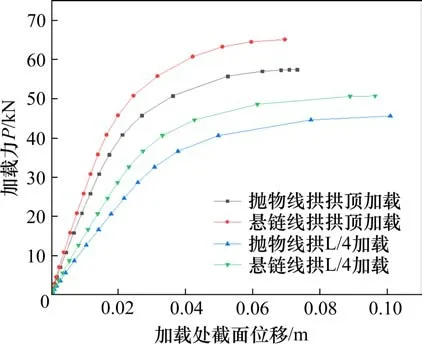
图17 承载力对比Fig.17 Comparison of bearing capacity

3.2 参数扩展分析

利用上文介绍的有限元法，以国内最大跨径的悬链线钢管混凝土单管拱桥-瓦石窝大桥为依托，分析不同含钢率、矢跨比、拱轴系数在不同加载方式下对面内承载力影响。主拱钢材采用Q345，管内混凝土采用C60。为了使参数分析结果满足工程需要和更具普遍性[1]，各关键参数取为：矢跨比为1/3～1/7，拱轴系数为1.2～2.3，以及含钢率为0.04～0.13。

图18 为不同加载方式、矢跨比、拱轴系数以及含钢率对钢管混凝土拱承载力影响效应图。由图中数据可知，不同加载方式对悬链线钢管混凝土拱的极限承载力影响较大，拱顶加载工况的极限承载力要大于L/4 处加载工况。因此，为保证拱的安全，钢管拱成拱后在施工后续结构时要避免拱承受过大的偏载。此外，悬链线钢管混凝土拱的极限承载力随着拱轴系数的增加而降低；随着矢跨比的增大，拱的极限承载力要增加，但增速变缓；随着含钢率的增加，拱的极限承载力呈线性增长。相对于含钢率和矢跨比而言，拱轴系数对钢管混凝土的承载力影响较小。

图18 不同参数对钢管混凝土拱影响效应Fig.18 Effect of different parameters on concrete filled steel tube arch

4 结论

1) 悬链线钢管混凝土拱在拱顶和L/4 处单点加载时，局部钢管发生明显变形但未出现屈曲现象，剖开钢管的混凝土出现横向裂缝，均为四铰破坏模式。拱最大变形均发生在加载处，拱顶加载工况拱破坏时变形基本呈现正对称分布，L/4 加载工况拱破坏时程反对称分布。L/4 加载工况下拱的变形和应变均大于拱顶加载工况，说明L/4 加载工况(偏载)更不利，钢管拱设计时须注意偏载对承载力的影响。

2) 悬链线钢管混凝土拱加载全过程的荷载位移曲线分为弹性、弹塑性，以及塑性破坏3个典型阶段。由拱顶加载和L/4 加载的应变分布可知，悬链线钢管混凝土拱截面总体呈受弯状态，在加载处弯矩最大，且钢管发生屈服。

3) 与抛物线钢管混凝土拱相比，悬链线钢管混凝土拱的钢管对核心混凝土的约束效应发挥的作用更早。当加载力达到55%的极限荷载时，外包钢管开始对内部混凝土产生约束作用，随后混凝土环向变形迅速增加，外部钢管开始发挥约束效应。

4) 不同加载方式、含钢率，以及矢跨比对悬链线钢管混凝土的承载力影响较大，拱轴系数影响较小。