基于低维流形先验的低剂量CT重建方法

牛善洲，梁礼境，李 硕，张梦真，邱 洋，刘汉明，李 楠

1.赣南师范大学数学与计算机科学学院，江西赣州341000

2.赣南师范大学赣州市计算成像重点实验室，江西赣州341000

3.赣南师范大学经济管理学院，江西赣州341000

X 射线计算机断层（computed tomography，CT）成像在疾病防治与诊断方面取得了巨大成就，其作为一种无痛、无创伤性的检查方法，可用于全身多脏器检查，是现代影像学的杰出代表[1]。CT 图像的质量与X 射线的辐射剂量紧密相关，剂量越高图像质量越好，但是过高剂量的X 射线照射会造成患者脱发、皮肤灼伤，甚至可能诱发癌症或者遗传性疾病[2-4]。针对CT检查过程中的X 射线照射剂量问题，世界卫生组织、国际放射委员会以及国际医学物理组织制定了X 射线照射剂量保证和剂量控制标准，极力主张X 线CT 检查应遵循实践正当性、防护最优化的原则，希望以最小的代价和剂量获取最好的CT 影像诊断效果。因此，在保证图像质量的前提下最大限度地减少X射线的辐射剂量已成为CT成像领域亟待解决的关键问题。

降低管电流或者管电压是实现低剂量CT成像最简单有效的方法，但是投影数据会受到量子噪声和电子噪声的污染，从而使得FBP 算法重建图像的质量严重退化，无法满足临床诊断的需求[5-6]。低剂量CT 图像重建方法主要分为基于图像域重建和基于投影域重建两大类。基于图像域的重建方法是在图像域中对待重建的图像进行系统建模，然后通过迭代算法求解目标函数进行图像重建[7-8]。但是，由于迭代重建需反复进行投影与反投影运算，导致运算量大，重建速度慢，无法满足快速诊断的需要。基于投影域的方法利用投影数据的噪声统计特性建立投影数据恢复模型，得到高质量的投影数据后利用FBP 算法重建最终CT 图像[9-15]。该类方法与图像域迭代重建方法相比计算时间大幅减少，在去除噪声的同时可以很好地保持图像的空间分辨率。Lu 等[16]通过大量的临床低剂量CT 实验以及相应的理论分析，提出经对数变换后的投影数据噪声近似满足均值和方差呈非线性关系的高斯分布。基于投影数据这一重要统计特性，Wang等[12-13，17]提出多种基于吉波斯随机场先验的惩罚加权最小二乘（penalized weighted least-squares，PWLS）低剂量CT 投影数据恢复方法，如基于KL 变换的惩罚加权最小二乘方法[13]、多尺度加权惩罚加权最小二乘方法[12]等。但Wang等提出的基于吉波斯随机场先验的惩罚加权最小二乘方法的目标函数使用的是二次惩罚函数，而在投影数据恢复过程中，二次惩罚函数对投影数据的均匀区域和边缘区域使用相同的惩罚权重会造成图像的边缘和结构细节信息的丢失，从而会导致重建图像的空间分辨率下降。

图像块流形的一个重要特性是其具有低维结构，并且包含丰富的结构信息。图像块可以视为嵌在高维空间中低维流形的点云，极小化图像块流形的维数可以作为先验信息进行图像恢复。低维流形先验将线性对象的低秩先验扩展到具有更复杂结构的数据对象上，其可以更好地恢复图像的结构细节信息。因此，将低维流形的维数作为先验信息引入到低剂量CT 投影数据恢复过程中，提出了一个基于低维流形惩罚加权最小二乘（penalized weighted least-squares based on low-dimensional manifold，PWLS-LDMM）的低剂量CT 投影数据恢复模型，通过极小化相应的目标函数可以得到理想的投影数据，再使用FBP 算法对恢复后的投影数据进行CT 重建。实验结果表明该方法在有效抑制低剂量CT图像噪声和伪影的同时可以很好地保持图像的边缘和结构细节特征。

1 模型与方法

1.1 PWLS重建模型

先前的研究工作表明[18]，在低剂量CT 扫描协议下经过系统校准和对数转换的投影数据近似遵循高斯分布，数据样本均值和方差之间满足如下的公式：

其中，I0是入射X线强度，是第i个探测器单元上投影数据（对数变换后）的均值，是电子噪声的方差。设y=(y1,y2,…,yM)T为系统校正和对数变换后的投影数据测量值，q=(q1,q2,…,qM)T为待估计投影数据的理想值，则基于PWLS的低剂量CT重建模型为：

1.2 低维流形先验

设投影数据q为m×n的矩阵，选取q中的任意一个像素点(i,j)，在像素点(i,j)处选取大小为s1×s2的图像块Ψx(q)，其中，s1和s2分别为图像块Ψx(q)的行数和列数，为s1×s2矩阵左上角的像素。对q中所有像素点的图像块Ψx(q)组合成q的点云Ψ(q)：

其中，d=s1×s2,Rd为d维的欧几里德空间。

基于微分流形理论，点云Ψ(q)可以模拟为一个嵌在Rd空间中的低维光滑流形M=∪l Ml，其中Ml是对应q中不同区域的流形，M为q的图像块流形。投影数据q的低维流形先验可以写为[19]：

其中，dim(M)为流形M的维数，αi(w)=wi为指标函数，且w=(w1,w2,…,wd)∈M,∇Mαi(w)为指标函数αi(w)在流形M上的梯度且为欧几里德范数。

1.3 PWLS-LDMM重建模型

PWLS-LDMM的投影数据恢复模型可以写为：

其中，p和q都为待恢复投影数据，T 为转置运算，Σ为对角矩阵，对角矩阵对角线上的元素为方差β2>0 为正则化参数为q的低维流形先验。

使用如下的交替优化算法求解PWLS-LDMM投影数据恢复模型：

其中，k为迭代次数。

由于式（6）的目标函数为光滑的二次凸函数，可以对其求导并令导数为零来进行求解。得到其解为：

其中，I为单位矩阵，Σ-1为对角矩阵Σ的逆矩阵，β1为正则化参数，(Σ-1+β1I)为对角矩阵。

使用交替优化法求解式（7），先固定流形更新投影数据，再固定投影数据更新流形。具体求解步骤如下：

（1）先固定流形初始值M(k)，通过求解下式得到指标函数α(k+1)i(i=1,2,…,d)和投影数据q(k+1)：

其中，Ψ*为Ψ的伴随算子，Ψ*Ψ为对角矩阵。

（2）通过指标函数对流形进行更新，公式如下：交替求解公式（6）、（7）得到恢复后的投影数据后，再使用FBP算法，即可重建出最终CT图像。

综上所述，基于低维流形先验加权最小二乘的低剂量CT重建方法的计算步骤可以写成如下所示：

步骤1 初始化令k=0；

步骤2 将qk代入式（6），通过式（8）得到pk+1；

步骤3 将pk+1代入式（7），通过式（9）~（13）得到αk+1和qk+1，并通过式（14）对流形进行更新；

步骤4 重复步骤2~步骤3，直至满足迭代终止条件；

步骤5 利用FBP算法将步骤3得到的投影数据qk+1重建出CT图像。

1.4 对比方法

为了验证PWLS-LDMM 方法的有效性，将其与传统的FBP方法，基于二次模先验的惩罚加权最小二乘方法[14]（penalized weighted least-squares via quadratic membrane，PWLS-QM）和基于字典学习先验的惩罚加权最小二乘（penalized weighted least-squares via dictionary learning，PWLS-DL）方法[20]进行比较。

PWLS-QM方法的目标函数为：

其中，Ni是投影数据中第i个像素的一阶邻域，wim在水平方向取值为1，在垂直方向取值为0.25。

PWLS-DL方法的目标函数为：

其中，D∈RL×K为训练字典，αs∈RL×1是含有少量非零元的向量，Es∈RL×K是从图像f提取的块矩阵，vs是拉格朗日乘子，γ是超参数。

1.5 实验设置

分别使用Shepp-Logan 体膜（如图1（a）所示）和XCAT 体膜（如图1（b）所示）以及临床数据实验来对所提出的PWLS-LDMM方法进行验证，并使用文献[21]中的方法仿真生成低剂量CT 投影数据。数值体膜实验中，CT成像几何采用扇形束和弧形探测器，X射线源到旋转中心和探测器的距离分别为570 mm 和1 040 mm，旋转角在[]0,2π 间采样值为1 160，每个采样角对应672个探测器单元，探测器单元的大小为1.407 mm。图像维数为512×512，像素大小为1 mm×1 mm。Shepp-Logan和XCAT 体膜室验的入射光子强度I0分别为5.0×104、3.0×104，电子噪声的方差σ2e都为10.0。在临床数据实验中的腹部投影数据，由商业单排CT 设备采集。X 射线源到旋转中心和探测器的距离分别为570 mm 和1 040 mm，旋转角在间采样值为1 160，每个采样角对应672个探测器单元，探测器单元的大小为1.407 mm。在球管电压为120 kV 下，分别获取400 mAs（高剂量）和50 mAs（低剂量）的CT 投影数据。重建图像的维数为512×512，像素大小为0.6 mm×0.6 mm。分别使用相对均方根误差（relative root mean square error，RRMSE），结构相似性指标[22]（structural similarity，SSIM）和特征相似性指标[23]（feature similarity，FSIM）对重建图像进行定量分析。使用MatlabR2020b（Ubuntu）编程，所有程序都在Intel®Reon®Gold 6234 2.33 GHz，16 核处理器，64 GB内存PC机上实现。

图1 数值体膜图像Fig.1 Digital phantom

2 实验结果与分析

2.1 Shepp-Logan体膜实验

图2为不同方法重建的Shepp-Logan 体膜图像。图2（a）为FBP算法重建的图像；图2（b）为PWLS-QM方法重建的图像；图2（c）为PWLS-DL 方法重建的图像；图2（d）为PWLS-LDMM方法重建的图像。从图2可以看出，FBP 方法重建的图像质量严重退化，存在大量的噪声和条形伪影。PWLS-GS重建的图像相比于FBP重建图像、噪声和伪影得到抑制，但仍含有一些噪声和条形伪影。PWLS-DL方法重建的图像噪声得到了一定程度上的抑制，但仍含有条形伪影。PWLS-LDMM 方法重建的图像中噪声和条形伪影都被有效抑制，同时可以保持边缘和细节结构特征。因此，本文提出的PWLSLDMM方法在抑制噪声伪影和保持图像分辨率方面都有良好表现，可以保持良好的图像一致性。

图2 不同方法重建的Shepp-Logan体膜图像Fig.2 Shepp-Logan images reconstructed by different methods

表1为Shepp-Logan 体膜重建图像的结构相似性、特征相似性和相对均方根误差。与FPB、PWLS和PWLSDL 方法相比，PWLS-LDMM 方法的相对均方根误差分别降低了64.87%、54.81%和7.02%。与FBP、PWLS-QM和PWLS-DL 方法相比，PWLS-LDMM 方法的SSIM 值分别提高了16.78%、1.88%和1.91%；FSIM 值分别提高了12.68%、2.73%和1.65%。PWLS-LDMM 方法重建的图像具有最高的SSIM 值和FSIM 值，即最接近于真实的体膜图像。

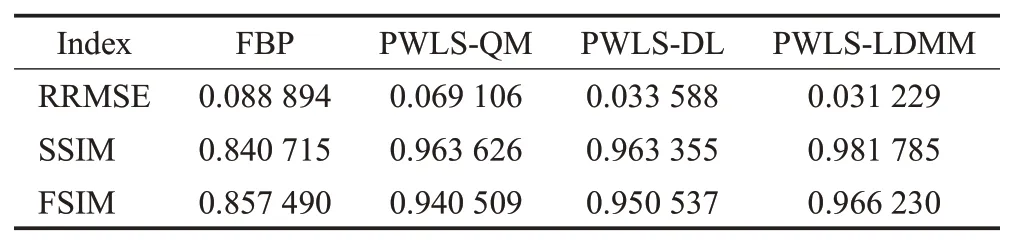
表1 Shepp-Logan体膜图像的RRMSE、SSIM和FSIMTable 1 RRMSE，SSIM and FSIM of Shepp-Logan

为了更清晰地比较各种方法对噪声和伪影的抑制效果，图3给出了图1中感兴趣区域（如图1（a）中红色方框所示）的局部放大图。与FBP、PWLS-QM 和PWLSDL 三种方法相比，PWLS-LDMM 方法能在有效去除噪声和伪影的同时可以保持图像的边缘信息和结构细节特征。进一步，使用SSIM 和FSIM 值对局部放大图进行定量分析。图4 给出了图3 中各重建结果的SSIM 值和FSIM 值。与FBP、PWLS-QM、PWLS-DL 方法相比，PWLS-LDMM 方法的SSIM 值分别提高了329.71%、11.74%和23.41%；FSIM 值分别提高了111.84%、8.31%和13.48%。PWLS-LDMM方法的SSIM和FSIM值均高于其他方法的SSIM 值和FSIM 值，即PWLS-LDMM 方法重建的图像最接近真实体膜。

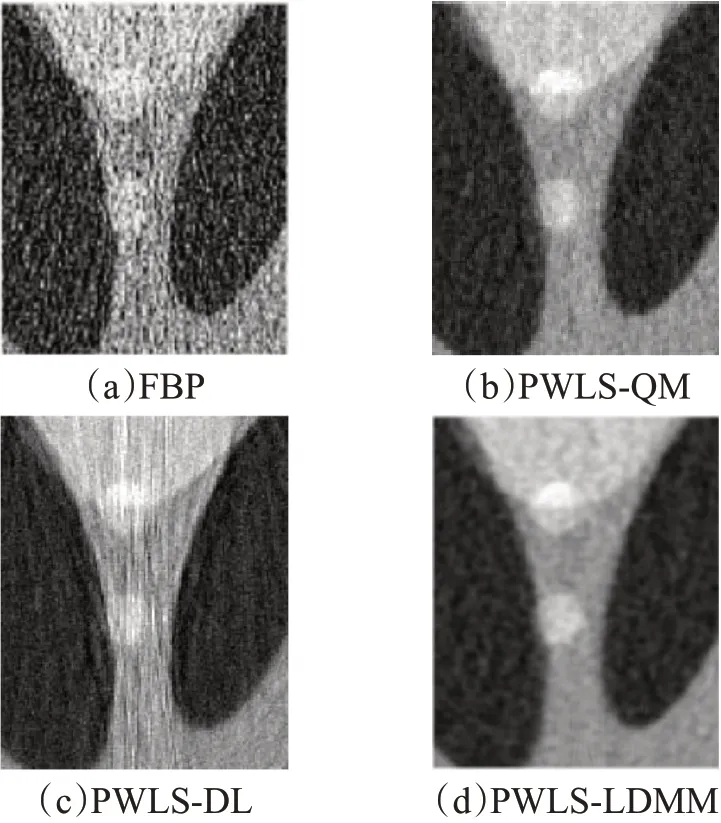
图3 Shepp-Logan体膜的局部放大图Fig.3 Zoomed-in views of Shepp-Logan phantom

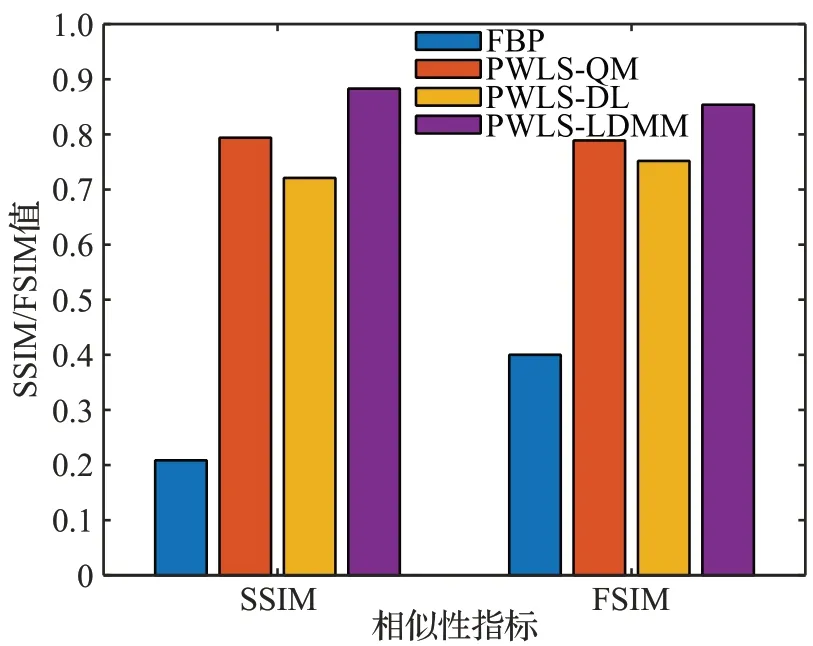
图4 图3中图像的SSIM值和FSIM值Fig.4 SSIM and FSIM values of images in Figure 3

2.2 XCAT体膜实验

图5为不同方法重建的XCAT 体膜图像。图5（a）为FBP方法重建的图像；图5（b）为PWLS-QM方法重建的图像；图5（c）为PWLS-DL 方法重建的图像；图5（d）为PWLS-LDMM 方法重建的图像。从图5 可以看出，FBP 方法重建的图像存在较多的噪声和条形伪影；PWLS-GS 重建的图像中仍含有一些噪声和条形伪影；PWLS-DL方法重建的图像噪声得到了一定程度上的抑制，但仍含有条形伪影；PWLS-LDMM方法重建的图像中噪声和条形伪影都被有效抑制。因此，本文提出的PWLS-LDMM方法在抑制噪声伪影和保持图像分辨率方面都有良好表现，对比其他三种方法得到了更优质的重建图像。

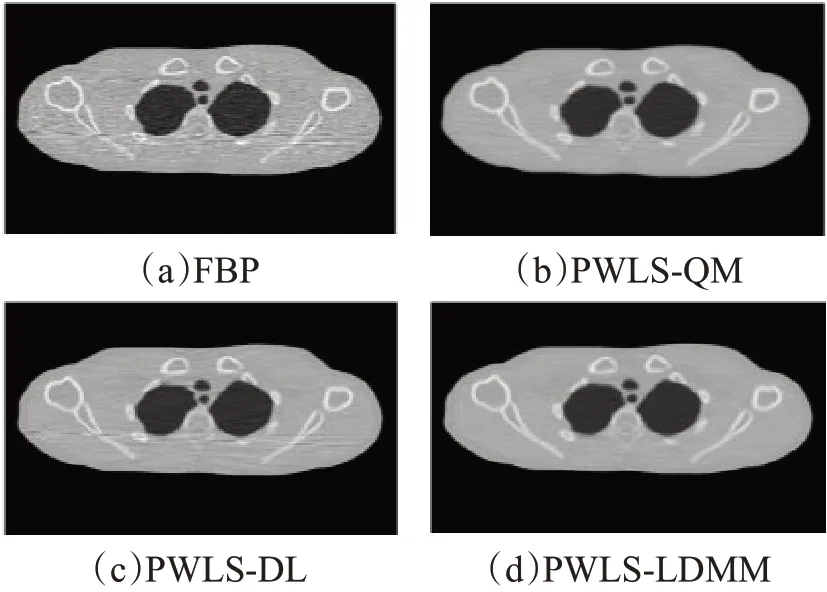
图5 不同方法重建的XCAT体膜图像Fig.5 XCAT images reconstructed by different methods

表2为XCAT 体膜重建图像的结构相似性、特征相似性和相对均方根误差。如表2所示，PWLS-LDMM方法与其他方法相比，在降低相对均方根误差方面有很好的表现。与FBP、PWLS-QM 和PWLS-DL 方法相比，PWLS-LDMM方法的相对均方根误差分别降低了37.46%、22.17%和11.48%。与FBP、PWLS-QM 和PWLS-DL 方法相比，PWLS-LDMM方法的SSIM值分别提高了3.33%、0.73%和1.22%；FSIM 值分别提高了0.83%、0.68%和0.71%。PWLS-LDMM 方法的SSIM 和FSIM 值均高于其他方法的SSIM 值和FSIM 值，即PWLS-LDMM 方法重建的图像最接近真实体膜。

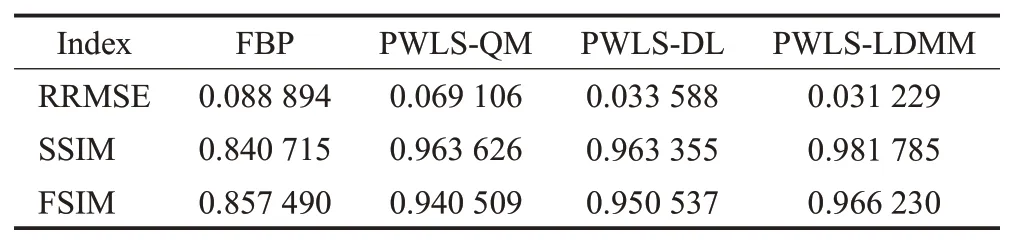
表2 XCAT体膜图像的RRMSE、SSIM和FSIM Table 2 RRMSE，SSIM and FSIM of XCAT images

同样，为了更清晰地比较各种方法对噪声和伪影的抑制效果，图6给出了图1中感兴趣区域（如图1（b）中大小为60×100 的红色方框所示）的局部放大图，并使用SSIM 和FSIM 值来对结果的感兴趣区域进行定量分析。图7 给出了图6 中各重建结果的SSIM 值和FSIM值。与FBP、PWLS-QM 和PWLS-DL 方法相比，PWLSLDMM 方法的SSIM 值分别提高了80.17%、8.97%和20.46%；FSIM 值分别提高了26.17%、4.98%和8.30%。PWLS-LDMM方法的SSIM和FSIM值均高于其他方法的SSIM 值和FSIM 值，即PWLS-LDMM 方法重建的图像最接近真实体膜。

图6 XCAT体膜图像的局部放大Fig.6 Zoomed-in views of XCAT phantom

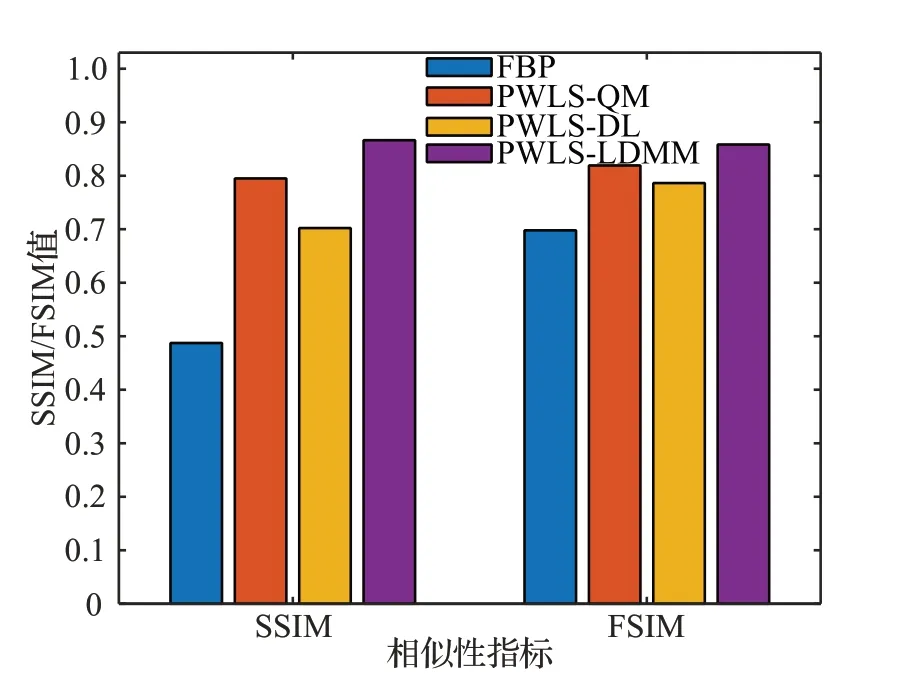
图7 图6中图像的SSIM值和FSIM值Fig.7 SSIM and FSIM values of images in Figure 6

2.3 临床数据实验

图8为临床腹部CT投影数据重建图像。图8（a）为400 mAs条件下FBP算法重建得到的高剂量图像，其作为金标准图像来对实验结果进行定量分析；图8（b）为50 mAs 条件下FBP 方法重建的图像；图8（c）为50 mAs条件下PWLS-QM 方法重建的图像；图8（d）为50 mAs条件下PWLS-DL方法重建的图像；图8（e）为50 mAs条件下PWLS-LDMM 方法重建的图像。从图中可以看出，本文提出方法在噪声滤除和边缘细节以及图像分辨率保持方面表现更为突出，优于对比方法。

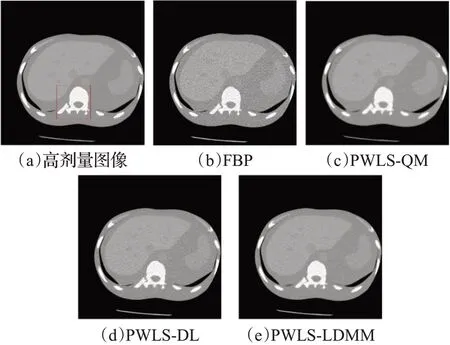
图8 临床数据重建图像Fig.8 Images reconstructed by clinical data

表3为低剂量临床数据重建的CT图像的结构相似性、特征相似性和相对均方根误差。如表3所示，PWLSLDMM 方法与其他方法相比，在降低相对均方根误差方面有很好的表现。与FBP、PWLS-QM 和PWLS-DL方法相比，PWLS-LDMM 方法的相对均方根误差分别降低了45.96%、25.61%和15.87%。与FBP、PWLS-QM和PWLS-DL 方法相比，PWLS-LDMM 方法的SSIM 值分别提高了19.12%、7.46%和8.63%；FSIM 值分别提高了4.37%、1.83%和1.14%。PWLS-LDMM 方法的SSIM和FSIM 值均高于其他方法的SSIM 值和FSIM 值，即PWLS-LDMM方法重建的图像最接近高剂量图像。

表3 低剂量临床数据重建的CT图像的RRMSE、SSIM和FSIMTable 3 RRMSE，SSIM and FSIM of low-dose CT images reconstructed by clinical data

进一步，为了更清晰地比较各种方法对噪声和伪影的抑制效果，图9给出了重建图像感兴趣区域（如图8（a）中红色方框所示）的局部放大图。图10给出了图9中各重建结果的SSIM值和FSIM值。与FBP、PWLS-QM和PWLS-DL 方法相比，PWLS-LDMM 方法的SSIM 值分别提高了46.88%、1.02%和26.71%；FSIM值分别提高了8.34%、2.59%和3.78%。

图9 临床数据重建CT图像的局部放大图Fig.9 Zoomed-in views of CT images reconstructed by clinical data

图10 图9中图像的SSIM值和FSIM值Fig.10 SSIM and FSIM values of images in Figure 9

3 结论

为了提高低剂量CT 重建图像的质量，将低维流形作为先验信息引入投影数据的恢复过程中，提出了一种基于低维流形先验的低剂量CT重建方法。数值仿真和临床数据实验结果表明，本文提出的低剂量CT 投影数据恢复模型在噪声和条形伪影抑制方面都取得了很好效果。为了验证PWLS-LDMM 方法的有效性，使用多种定量指标对重建结果进行分析与比较。与FBP、PWLS-QM 和PWLS-DL 对比方法相比，PWLS-LDMM方法在相对均方根误差、结构相似性和特征相似性等方面均有上佳的表现。PWLS-LDMM方法在噪声去除，条形伪影抑制已经结构细节保持方面明显优于对比方法。