多类属性加权与正交变换融合的朴素贝叶斯
刘海涛,陈春梅,庞忠祥,梁志强,李 晴
西南科技大学信息工程学院,四川绵阳621002
朴素贝叶斯(Naive Bayes,NB)算法具有简单、高效、可解释性等优点,但是它的属性条件独立性假设在现实中很少成立[1],这将降低在现实中具有属性依赖性样本的分类性能。目前,学者们为了减弱属性条件独立性假设,已提出众多改进方法,大致可分为七类:结构扩展[2-6]、属性选择[7-11]、属性加权[12-14]、实例选择[15-16]、实例加权[17-19]、微调[20-21]和属性变换[22]。
结构扩展是一种通过添加有向弧来显式地表示属性依赖的方法。如何精确地寻找属性依赖关系是这类方法需要解决的问题。为了解决这一问题,Friedman等人[2]提出了树增强朴素贝叶斯(tree augmented Naive Bayes,TAN),属性依赖性由树状结构表示。在TAN中,类节点直接指向所有属性节点,每个属性节点最多只有一个来自另一个属性节点的父节点。事实上,TAN在学习属性依赖性方面非常有效,但同时TAN 也带来了相当大的计算成本。为了降低计算成本,Webb等人[3]提出了一种称为平均单依赖估计(averaged one-dependent estimator,AODE)的集成模型。AODE将每个属性依次视为所有其他属性的父节点,从而构建多个超级父单依赖性估计器(super-parent one-dependent estimator,SPODE)。然后通过直接平均所有合格SPODE 的类成员概率来产生最终预测结果。除了AODE,Jiang等人[4]提出了另一种模型,称为隐藏朴素贝叶斯(hidden Naive Bayes,HNB)。在HNB中,为每个属性创建一个隐藏的父节点,并且隐藏父节点具有显式语义。简单来说,每个属性的隐藏父级可以看作是汇聚了所有其他属性的影响。因此,HNB 避免了学习最优结构的高计算复杂性,但考虑了所有属性的影响。张文钧等人[5]提出了一种基于特征增广的生成-判别混合模型的构建方法。该方法利用特征增广的思想对模型进行结合,从而减少了时间复杂度,增强了原始属性的内在信息。最后将NB和HNB分别作为生成模型,将LR(logistic regression)作为判别模型,构建了NB-LR和HNB-LR两种混合算法。
虽然结构扩展是有效的,但学习最佳结构仍然相当困难。近年来,诸多学者开始关注另一种改进NB算法的方法,即属性选择。由于数据集中的多余属性不仅会增加分类模型的计算量,还会影响其分类性能。所以,属性选择方法[7]剔除了多余属性,保留了样本中贡献度较高的相关属性,在不改变NB结构的情况下,使其具有简单、高效等特点[10]。但是在实际中样本的不同属性对该样本的分类结果会产生不同的影响,属性选择方法没有考虑不同属性组合在分类过程中的不同重要性。
属性加权[12]方法则考虑了不同属性的权重问题。它通过为每个属性分配一个不同的权重,来表示不同属性对分类的重要程度。Jiang 等人[14]提出了一种基于相关性的属性加权(correlation-based feature weighting,CFW)朴素贝叶斯。在CFW中,每个属性的权重首先被定义为互相关性(属性与类之间的相关性)和平均相互冗余(属性之间的冗余)之间的差值。然后,再对权重进行s型变换,以确保权重值在一个规定的范围内。实验结果表明,CFW 的分类精度高于NB,同时还保持了最终模型的简单性。宁可等人[23]针对多维连续型数据,通过高斯分割对属性类别不同的多维连续型数据集进行离散化处理,并使用拉普拉斯校准、属性关联和属性加权方法改进了朴素贝叶斯分类的过程。丁月等人[24]通过JS 散度公式来衡量特征项为文本带来的信息量,然后结合类别内外的词频、文本频以及用变异系数修正过的逆类别频率对JS 散度作进一步的调整,最后将计算的属性权重加入到朴素贝叶斯公式中,从而提升了朴素贝叶斯算法在文本分类中的性能。赵博文等人[25]利用泊松分布模型对文本特征词进行加权,并结合NB算法对文本进行了分类。上述的属性加权方法是通过给样本中的属性赋予权重,来量化不同的属性对分类的影响。最近,Zhang 等人[26]认为原始属性空间提供的信息可能不足以进行分类。因此,为了获得原始属性空间的潜在信息,Zhang等人提出了一种双阶段的属性增强和加权朴素贝叶斯(attribute augmented and weighted Naive Bayes,A2WNB)算法。在A2WNB中,首先建立多个随机单依赖估计器用于训练样本的分类。然后,将预测的类别作为潜在属性并和原始属性连接来得到增强属性。最后,通过最大化模型的条件对数似然函数来优化增强属性的权重。此外,Zhang 等人[27]提出了一种多视图的属性加权朴素贝叶斯(multi-view attribute weighted Naive Bayes,MAWNB)算法。该算法首先构建多个超级父单依赖估计和随机树,然后利用它们中的每一个依次对每个训练实例进行分类,并使用它们的所有预测类标签来构建两个标签视图,最后通过最小化每个视图中的负条件对数似然函数来优化每个类中的每个属性的权重。
目前,一些研究人员又将他们的注意力转向到了另一种更加细致的属性加权方法,文献[28-32]可通称为属性值加权,并且通过对属性值的加权,可以使分类器性能得到进一步地提高。Yu 等人[28]假设高度预测的属性值应该与类属性强相关,但与其他属性值不相关,并通过计算相关性和平均冗余之间的差值,为属性值分配不同的权值。秦锋等人[29]通过计算属性值与类别之间的关联性来获取不同属性值在后验概率中的加权系数,从而提升朴素贝叶斯分类的准确率。Zhang等人[32]通过考虑属性值的水平粒度和类标签的垂直粒度来评估属性之间的依赖性,并有区别地为每个类的属性值分配一个特定的权重。
属性变换主要是对样本属性之间的线性关系进行研究,如李福祥等人[22]提出的正交变换改进的朴素贝叶斯(Naive Bayes of orthogonal transformation,OTNB)算法,此算法是通过数值标记将离散属性变换为连续属性,之后对连续属性和数值标记后的离散属性进行正交变换,增强属性之间的相互独立性,去除属性之间的线性关系,从而贴近了朴素贝叶斯算法的属性条件独立性假设。
为了保留NB 算法的简单性,人们对朴素贝叶斯算法进行了微调,微调是指在第一阶段建立标准的NB模型,在微调阶段将每个训练实例都进行分类,然后判断对训练实例的分类结果正确与否,再根据判断结果对原朴素贝叶斯算法进行微调。Diab & Hindi 将朴素贝叶斯算法中的概率估计问题转化为一个优化问题[33],并融合了差分进化(differential evolution,DE)、遗传算法(genetic algorithms,GA)和模拟退火(simulated annealing,SA)三种算法,从中获得启发。实验结果表明,该方法在不同的领域得到了广泛的应用,特别是在样本的基本分布不能通过训练样本充分体现时,该方法表现出了一定的优越性。Hindi等人[34]提出了一个用于文本分类的微调朴素贝叶斯(fine-tuning NB,FTNB)的分类符集成。他们修改了FTNB中的更新方程,使该方法产生不同的分类器。然后建立了一个FTNB集成分类器,以期望显著提高分类的准确性。实验表明,该算法在16 个基准文本分类数据集中的分类性能有明显提升。Zhang等人[35]提出了一种微调属性加权朴素贝叶斯(fine tuning attribute weighted NB,FTAWNB),是在对朴素贝叶斯算法进行属性加权改进的基础上进行了微调,它减少了朴素贝叶斯算法对测试样本的分类时间,并提高了算法的精度。
上述的属性和属性值加权方法是针对离散属性或连续属性离散化之后的属性值进行加权[32],这会导致连续属性的内在信息丢失。因此,本文将离散属性和连续属性进行区分,只给离散属性和离散属性值赋予权重,而对于连续属性使用正交变换的方法消除连续属性之间的线性关系。这样一来既保留了离散和连续属性的内在信息,还量化了离散属性和离散属性值之间的相互关系以及对其所属样本分类的贡献程度。
1 朴素贝叶斯分类算法的改进
针对多维混合属性样本,一般的朴素贝叶斯改进算法是先将连续属性离散化[32]或离散属性连续化[22]之后再对算法进行训练。本文首先对离散属性进行加权,对连续属性进行正交变换,然后对两者的条件概率分别计算,最后将计算结果进行融合,从而得到多类属性加权与正交变换融合的朴素贝叶斯(Naive Bayes fusion of multiple attribute weighting and orthogonal transformation,MAWOTFNB)算法,以此来保留离散和连续属性的内在信息,削弱属性条件独立性假设给NB算法造成的影响。
1.1 改进算法的框架
本文提出的MAWOTFNB 算法一方面将多类离散属性和离散属性值权重加入到离散属性“频率计数估计”的条件概率计算中,然后对正交变换后的连续属性使用“概率密度函数”的条件概率计算方式进行计算。另一方面,将两种不同的条件概率计算方式进行融合并加入类属性权重,得到多维混合属性的后验概率计算公式。因此,MAWOTFNB算法可以对样本中离散属性和连续属性的条件概率进行区分计算,并继承了离散属性和离散属性值加权方法、正交变换方法的优点,从而保留了离散属性与连续属性的内在信息。MAWOTFNB算法使用式(1)对测试样本的类别进行预测。
其中,xi为测试数据集中的第i个测试样本,Ĉ(xi)是测试样本xi的类别预测函数,C是类集合,cd为类集合C中的第d个类,Dd为类cd中的离散属性标识,Sd为类cd中的连续属性标识。W为权重集合,且W={Wjkd,Wj,aj,Wjk},集合中Wjkd为类cd中第j个离散属性的取值为aj关于第k个离散属性取值为ak的联合离散属性值权重,Wj,aj为离散属性值aj的权重,Wjk为样本中第j个离散属性与第k个离散属性的联合离散属性权重。xiD为离散属性向量,xiS为连续属性向量。权重集合W中的各权重、P̂Dd(xiD|cd)和P̂Sd(xiS|cd)的定义见1.2节和1.3节,先验概率P̂(cd)由式(2)表示:
其中,Nd为训练数据集的类cd中的样本数量,N为训练数据集中样本的数量,D为训练数据集中类的数量,Wd为类cd的权重,其定义见1.2节。图1为MAWOTFNB算法框架。

图1 MAWOTFNB算法框架Fig.1 MAWOTFNB algorithmic framework
1.2 离散属性加权
1.2.1 类特定的联合离散属性值加权
文献[36]中的朴素贝叶斯条件概率计算公式是将待测样本不同属性的取值对此样本属于某个类别的支持度平等对待的,即每个离散属性值的权重都默认为1,这样一来在很大程度上限制了朴素贝叶斯分类器的分类精度。针对上述问题,本文通过式(3)构造类特定的联合离散属性值权重Wjkd:
其中,njd和nkd分别是类cd中第j个离散属性和第k个离散属性的取值数量,且1 ≤j≤nD,1 ≤k≤nD,nD是样本离散属性的数量,Count(aj,ak,cd)代表类cd中第j个离散属性和第k个离散属性取值为aj和ak的样本数量,Count(ak,cd)代表类cd中第k个离散属性取值为ak的样本数量,Wjkd表示在类cd中第j个离散属性取值为aj关于第k个离散属性取值为ak的联合离散属性值权重。Wjkd的取值是由Count(aj,ak,cd)、Count(ak,cd)、njd以及nkd共同决定的,且在训练数据集固定情况下,其取值确定后不会再改变。若njd=nkd,Count(ak,cd)=Count(aj,cd),Count(aj,ak,cd)=Count(ak,aj,cd),则Wjkd=Wkjd。Wjkd越大表示类cd中第j个离散属性的取值aj和第k个离散属性的取值ak所在样本属于此类别的支持度越大。
为了进一步说明离散属性值与类之间、离散属性值之间的相关程度,本文使用基于相关互信息的方法来对其相关性进行衡量。将单个离散属性值的权重由离散属性值与类之间以及离散属性值之间相关性的乘积得到,具体计算步骤如下。
步骤1 离散属性值与类标签c的相关性、离散属性值aj和ak的相关性使用相关互信息进行度量,分别由式(4)和式(5)给出:式(4)中的I(aj,c)是离散属性值aj与类标签c之间的相关互信息,P(aj,cd)是离散属性值aj与类属性值cd的联合概率,P(aj)和P(cd)分别为离散属性值aj和类属性值cd的先验概率。式(5)中的I(aj,ak)是离散属性值aj和ak之间的相关互信息,P(aj,ak)是离散属性值aj和ak的联合概率,P(aj)和P(ak)分别为离散属性值aj和ak的先验概率。
步骤2 使用式(6)和式(7)分别对I(aj,c)和I(aj,ak)进行归一化。
其中,nD是离散属性的数量,R(aj,c)和R(aj,ak)分别是归一化之后的离散属性值与类之间、离散属性值之间的相关互信息,可以将其用于计算单个离散属性值的权重。
步骤3 单个离散属性值权重由式(8)定义:
其中,Wj,aj为离散属性值aj的权重,它用来量化离散属性值aj对样本分类的贡献程度,且在训练数据集固定情况下,其取值确定后不会再改变。
1.2.2 联合离散属性加权
样本中的每一个属性对样本的重要程度是不同的,但是在文献[36]的朴素贝叶斯判定准则中是将每个属性对样本分类的贡献程度都默认为1,这在现实应用中是不可行的。因此,本文采用基于条件互信息的离散属性加权方法为每个离散属性分配不同的权重,以进一步提高分类器的性能。离散属性Aj与Ak的条件互信息由式(9)定义:其中,nD是离散属性的数量,D为训练数据集中类别的数量,I(Aj,Ak|c)是在已知类标签c的情况下观察Ak的取值带来关于Aj的信息量,P(aj,ak,cd)为离散属性值aj和ak与类属性值cd的联合概率,P(aj,ak|cd)为离散属性值aj和ak关于类cd的联合条件概率,P(aj|cd)和P(ak|cd)分别为离散属性值aj和ak关于类cd的条件概率。
由离散属性Aj与Ak的条件互信息获取联合离散属性权重由式(10)定义:
其中,Wjk为样本第j个与第k个离散属性的联合离散属性权重,且在训练数据集固定情况下,其取值确定后不会再改变。
1.2.3 类属性值加权
分类器是给定一个输入(测试样本),判断此输入所属的类别信息。而在分类器训练过程中由于训练数据集中每个类别之间的样本数量存在差异,则训练出来的分类器算法对测试样本的类别预测结果更倾向于训练样本数量比较多的类。由于训练数据集中可能存在某一类中的样本数量很少,而某一类中的样本数量较多的情况,这些不平衡的数据集会导致测试样本的条件概率和后验概率的计算结果受到极大的影响[37],从而影响分类器的性能。针对上述问题,本文使用类属性值权重来降低类中样本稀疏性对分类器性能造成的负面影响。其定义如式(11)所示:
其中,Wd为类cd的权重,在训练数据集固定情况下,其取值确定后不会再改变。N为训练数据集中样本的数量,D为训练数据集中类别的数量,Nd为训练数据集的类cd中的样本数量。
结合上述加权方法并假设离散属性向量为xiD=(a1,a2,…,anD),则基于离散属性加权的条件概率计算由式(12)定义:
式(13)中,P(aj|cd)是离散属性值aj关于类cd的条件概率,|Daj,cd|是类cd中离散属性值为aj的样本数量,njd是类cd中第j个属性的取值数量,Nd为训练数据集的类cd中的样本数量。式(14)中,P(ak|aj,cd)是离散属性值ak关于离散属性值aj和类cd的联合条件概率,|Daj,ak,cd|是训练数据集的类cd中第j个属性与第k个属性分别取值为aj与ak的样本数量,nkd为训练数据集的类cd中第k个属性的取值数量。
1.3 连续属性正交变换
基于连续属性正交变换的朴素贝叶斯算法利用正交变换的方法,结合朴素贝叶斯的属性条件独立性假设将属性之间的线性关系进行了消除,并且削弱了朴素贝叶斯分类器的属性条件独立性假设所带来的影响。因为在某些数据集中样本会存在既有离散属性又有连续属性的情况,本文为了保留离散和连续属性的内在信息,对样本中的离散属性与连续属性的条件概率进行区分计算。因此,本文对样本中的连续属性使用正交变换的方法,来去除连续属性之间的线性关系。针对连续属性的正交变换、概率密度函数的计算步骤如下。
步骤1 设有样本集为XS={x1S,x2S,…,xNS},每一个样本中的连续属性由xiS=(anD+1,anD+2,…,an)确定,训练数据集中每个连续属性在类cd中的样本均值μj,d使用式(15)计算:
其中,Nd为训练数据集的类cd中样本的数量,aij为第i个样本的第j个连续属性的值,且nD 步骤2 由步骤1 得到的每个类中连续属性的样本均值向量,通过式(16)求协方差矩阵。 步骤3 计算步骤2得到的类cd中连续属性的协方差矩阵Md的特征值与特征向量。在Md的特征值存在重根的情况下,通常是先将特征向量施密特正交化,然后单位化,即可获得相似对角化所需的可逆正交矩阵P;如果没有出现重根的情况,就只需对特征向量进行单位变换,然后获得可逆正交矩阵P,并使得PTMd P=Λ。 步骤4 令yiS=PT(xiS-μd),i=1,2,…,Nd,并计算类cd中对连续属性样本xiS正交变换后的y样本集{y1S,y2S,…,yNdS}中的样本均值向量和方差向量 步骤5 假设正交变换后的连续属性的概率密度函数服从正态分布,即,其中y∙j表示样本yiS的第j个属性,和分别是类cd中的样本正交变换之后在第j个属性上的样本均值和方差,则其概率密度函数由式(17)计算: 由于正交变换之后的连续属性消除了线性关系,满足连续属性之间相互独立的假设,则连续属性的概率密度函数由式(18)计算: 将上述基于离散和连续属性的条件概率计算方式进行融合,得到本文所改进的朴素贝叶斯算法由式(1)表示,详细的训练和分类过程分别使用算法1 和算法2描述。 算法1 MAWOTFNB-Training 输入:训练数据集。 (1)计算离散属性值aj和ak在类cd中共现的样本数量Count(aj,ak,cd)和离散属性值ak在类cd中出现的样本数量Count(ak,cd),统计类cd中第j个属性和第k个属性的取值数量njd和nkd,其中1 ≤j≤nD,1 ≤k≤nD。 (2)由式(3)计算联合离散属性值权重Wjkd。 (3)由式(4)和式(5)计算各离散属性值的I(aj,c) 和I(aj,ak)。 (4)由式(6)和式(7)对各离散属性值的I(aj,c)和I(aj,ak)进行归一化得到R(aj,c)和R(aj,ak)。 (5)由式(8)计算各单个离散属性值权重Wj,aj。 (6)由式(9)计算各离散属性的I(Aj,Ak|c)。 (7)由式(10)计算联合离散属性权重Wjk。 (8)将Wjkd、Wj,aj、Wjk组成集合W={Wjkd,Wj,aj,Wjk}。 (9)由式(11)计算类cd的权重Wd。 (10)将权重Wd代入式(2)计算先验概率 (11)计算训练数据集类cd中连续属性的样本均值向量μd及正交矩阵P。 (12)对训练数据集类cd中每一个样本的连续属性进行正交变换得到y={y1S,y2S,…,yNdS}。 算法2 MAWOTFNB-Classification 输入:W、P̂(cd)、μd、P、y、单个待分类样本xi。 输出:待分类样本xi的类别预测结果 (1)取出待分类样本xi的连续属性向量xiS,利用式yiS=PT(xiS-μd)对xiS进行正交变换,并将yiS放到y样本集中。 (2)计算y样本集的样本均值向量μ′d与方差向量σ′d。 (3)由式(18)计算关于类cd的连续属性正交变换之后的概率密度函数 (4)将权重集合W以及待分类样本xi的离散属性向量xiD代入式(12)计算离散属性条件概率 (5)将待分类样本xi的连续属性正交变换结果yiS从y样本集中移除。 (7)预测待分类样本xi的类别 在现实生活中的数据采集过程中会遇到许多未知的问题,这样会导致采集到的数据存在一定的错误,包括数据缺失、噪声数据等。数据缺失的类型有很多种,比如缺失数量的差异、缺失变量的差异等。为了便于数据的预处理,现在一般是从缺失值数量和结构上进行区分,根据包含缺失值变量的个数,可分别将其分为单个变量和多个变量的缺失[38],如表1 所示。单个变量缺失表示要分析的数据集样本中只有一个缺失属性值,而多个变量的缺失表示要分析的数据集样本中存在两个或两个以上的属性有缺失值[38]。表1 中的xi表示第i个样本,A1、A2、A3分别表示样本中第1、第2、第3 个属性,“1”表示含有属性值,“0”表示缺失属性值。 表1 单变量缺失与多变量缺失的表示Table 1 Univariate deletion and multivariable deletion 数据预处理的方法有很多,主要包含将含有缺失属性值的样本进行删除、对样本中缺失的属性值进行补充、将错误数据或未知数据搁置这三种方法来处理存在问题的数据[38]。若训练数据集中某个样本的某个或多个属性存在缺失值就直接删除的话,很有可能会丢失重要的分类信息。如果对这些缺失数据进行搁置,会对分类器的类别预测准确率造成很大的负面影响[38]。本文使用的数据集包括9 个“UCI 机器学习数据集”和1 个“Poor Students(实测)”的贫困生数据集。其中,Poor Students(实测)数据集来源于我校校园一卡通的整理数据。对数据集中的缺失数据均采用统计学的众数原理[39]进行插值,即对类中的某个样本的某个属性缺失值使用在该类中其他所有样本在该属性上出现次数最多的属性值进行补充。 为了验证本文所提出的多类属性加权与正交变换融合的朴素贝叶斯(MAWOTFNB)算法的有效性和适用性,本文使用9 个“UCI 机器学习数据集”和1 个“Poor Students(实测)”的贫困生数据集,利用“分层k折交叉验证”的验证方式[40]对NB、OTNB、FTAWNB、NB-LR、HNB-LR、A2WNB、MAWNB以及MAWOTFNB算法进行对比。其中NB 为基础分类算法;OTNB 代表了使用属性变换方法改进的算法;FTAWNB 代表了使用微调和属性加权方法改进的算法;NB-LR 和HNBLR 代表了使用结构扩展方法改进的算法;A2WNB 和MAWNB代表了使用双阶段属性加权方法改进的算法。 本文所使用的“分层k折交叉验证”的验证步骤如下。 步骤1 随机使用不同的划分折重复pk次,且pk=k,每次将数据集划分为k个大小相似且类间样本数量比例保持划分前的互斥子集。 步骤2 依次将每次划分的k-1 个子集的并集作为训练集,剩余的子集作为测试集对算法进行验证。 步骤3 记录每次划分中的平均分类准确率。 步骤4 获取pk次划分中平均准确率最高的一次,将此次分折作为“分层k折交叉验证”中k的取值。 上述步骤3 中的“准确率”表示类别预测正确的样本数占测试样本总数的比例。“分层k折交叉验证”原理如图2所示。 图2 分层k 折交叉验证原理图Fig.2 Schematic diagram of layered k-fold crossed verification 本文所使用数据集的具体描述如表2所示。 为了准确评估本文改进的朴素贝叶斯算法在分类任务中的表现,本文选择由“分层k折交叉验证”所得到的准确率和加权平均F1 值,即Fwa作为算法的性能评价指标,其计算公式分别由式(19)和式(20)表示。 其中,accuracy是各算法的分类准确率,m是测试样本的总数,pk是“分层k折交叉验证”中第k折验证重复的次数,m1k,m2k,…,mpkk是每次k折验证时类别预测正确的测试样本数量。 其中,L是测试样本集的类别预测结果中的类别个数,counti为第i个类的样本数量,Fi是将样本类别进行正负化之后,第i个类为正类,其他类为负类时的F1值,由式(21)定义: 其中,Precisioni和Recalli分别为测试样本被分到第i个类的查准率和召回率,Precisioni和Recalli由式(22)和式(23)表示: 式(22)中的TPi是正确分类到第i个类的样本数量,FPi是把其他类的样本分到第i个类的样本数量。式(23)中的FNi是把第i类的样本分到其他类的样本数量。 本文算法与其他分类算法的时间复杂度对比如表3所示。表3 列出了各算法的训练时间复杂度和预测时间复杂度,其中,m表示训练数据集中类别的个数;n表示属性的个数;t表示训练数据集中的样本个数,v表示属性值的平均数量;f表示FTAWNB 算法在第二阶段训练的循环次数;nD表示离散属性的个数;nS表示连续属性的个数。由表3可知,由于本文的MAWOTFNB算法在训练阶段首先将数据集中的离散属性和连续属性进行了区分,然后利用贡献度与相关互信息的方法量化了离散属性和离散属性值的权重,此过程的时间复杂度为;接着本文又利用正交变换方法对连续属性进行了正交变换,此过程的时间复杂度为O(tnS) ;因此,MAWOTFNB 算法的时间复杂度为各算法在各数据集上的训练时间如表4所示,训练时间对比图如图3所示,表4中的加粗字体为算法在当前数据集上训练时,耗时最多的算法训练所用的时间。 表3 各算法时间复杂度Table 3 Time complexity of each algorithm 表4 各算法在各数据集上的训练时间Table 4 Training time of each algorithm on each dataset单位:s 图3 各算法在各数据集上的训练时间对比Fig.3 Comparison of training time of each algorithm on each dataset 由表4 和图3 可知,NB-LR、HNB-LR、A2WNB 和MAWNB 算法在Adult 和Mushroom 数据集上的训练时间存在激增,而本文的MAWOTFNB 算法仅在Adult 数据集上的训练时间微有增加。由表2 可知,Adult 和Mushroom数据集相较于表中其他数据集中的样本数和属性数较多,特别是Adult 数据集中的样本数量达到了48 842个,属性个数达到了14个。因此,NB-LR、HNB-LR、A2WNB 和MAWNB 算法易受训练数据集中的样本个数和属性个数的影响,而本文的MAWOTFNB算法仅在训练数据集中的样本个数较多时,训练所耗时间才稍有增加。MAWOTFNB 算法在各数据集上的平均训练时间,比NB算法仅高0.015 s,比OTNB算法减少了0.016 s,和FTAWNB算法相等,比NB-LR算法减少了0.512 s,比HNB-LR减少了0.485 s,比A2WNB算法减少了0.109 s,比MAWNB算法减少了0.133 s。 本文在9 个“UCI 机器学习数据集”和1 个“Poor Students(实测)”的贫困生数据集上对比了NB、OTNB、FTAWNB、NB-LR、HNB-LR、A2WNB、MAWNB 和MAWOTFNB算法的性能评价指标。表5列出了本文改进的朴素贝叶斯算法与其他比较对象在每个数据集上的分类准确率。表6 展示了实验获得各算法在各数据集上的Fwa值。表5和表6中加粗的数字为该数据集上获得的最高分类准确率和Fwa值,本文将每个算法在10个数据集上的平均分类准确率和平均Fwa 值汇总在了表格底部。 表5 各算法在各数据集上的分类准确率Table 5 Classification accuracy of each algorithm on each dataset单位:% 表6 各算法在各数据集上的Fwa 值Table 6 Fwa values of each algorithm on each dataset单位:% 为了分析各分类算法在各数据集中的分类效果,使用簇状柱形图对比各算法的分类准确率、Fwa 值,分别如图4、图5所示。分析结论如下: 图4 各算法在各数据集上的分类准确率对比Fig.4 Comparison of classification accuracy of each algorithm on each dataset 图5 各算法在各数据集上的加权平均F1对比Fig.5 Comparison of weighted average F1 values of each algorithm on each dataset (1)OTNB算法忽略了离散属性取值先后顺序的不确定性,直接对其进行连续化操作,导致离散属性原有信息丢失。从表5 和表6 中可知,此算法的平均分类准确率和平均Fwa 值都是最低的,在实验数据集上的平均分类准确率仅有73.79%,平均Fwa 值仅有74.31%,其可视化对比图见图4和图5的最后一簇。 (2)相比于OTNB,FTAWNB 算法结合了微调和属性加权的方法。由表5 和表6 可知,其平均分类准确率达到了82.81%,比OTNB 算法高了9.02 个百分点;平均Fwa 值达到了80.58%,比OTNB 算法高了6.27 个百分点,其可视化对比图见图4和图5的最后一簇。 (3)相比于FTAWNB,NB-LR 和HNB-LR 算法使用结构扩展的方法来构建混合分类算法。由表5和表6可知,NB-LR 算法的平均分类准确率达到了83.29%,比FTAWNB 算法高了0.48 个百分点,平均Fwa 值达到了82.78%,比FTAWNB 算法高了2.2 个百分点;HNB-LR算法的平均分类准确率达到了82.92%,比FTAWNB 算法高了0.11 个百分点,平均Fwa 值达到了82.88%,比FTAWNB 算法高了2.3 个百分点,其可视化对比图见图4和图5的最后一簇。 (4)相比于NB-LR 和HNB-LR,A2WNB 算法利用双阶段的属性加权改进算法来获得增强属性。由表5和表6可知,其平均分类准确率达到了85.34%,比NB-LR算法高了2.05个百分点,比HNB-LR算法高了2.42个百分点;平均Fwa值达到了85.14%,比NB-LR 算法高了2.36 个百分点,比HNB-LR 算法高了2.26 个百分点,其可视化对比图见图4和图5的最后一簇。 (5)与A2WNB 类似,MAWNB 算法是使用双阶段属性加权算法来构建两个标签视图,从而改进NB 算法。由表5和表6可知,其平均分类准确率达到了85.56%,比A2WNB算法高了0.22个百分点;平均Fwa值达到了85.82%,比A2WNB 算法高了0.68 个百分点,其可视化对比图见图4和图5的最后一簇。 (6)不同于前面所述的OTNB、FTAWNB、NB-LR、HNB-LR、A2WNB 以及MAWNB 算法,本文所提出的MAWOTFNB 算法在数据集上的平均分类准确率达到了92.75%,在同等条件下,不仅比NB高11.93个百分点,比OTNB高18.96个百分点,还比目前最新的FTAWNB、NB-LR、HNB-LR、A2WNB 以及MAWNB 算法分别高9.94 个百分点、9.64 个百分点、9.83 个百分点、7.41 个百分点、7.19个百分点,且其平均Fwa值达到了92.22%,同样高于上述分类算法。这说明了本文算法将离散和连续属性进行区分处理,更加有利于对多维混合属性数据集的分类任务,其可视化对比图见图4和图5的最后一簇。 为了进一步阐述各分类算法在各数据集上的分类优势,表7展示了各算法在各数据集上所获得准确率的WDL,其中W、D、L 分别为各算法分类准确率两两比较中获胜数据集的数量、持平数据集的数量和落后数据集的数量。图6 为各算法WDL 值对比的三维柱形图可视化。 表7 各算法的WDL值Table 7 WDL value of each algorithm 图6 各算法的WDL值对比Fig.6 WDL value comparison of each algorithm 由表7 可知,本文的MAWOTFNB 算法在实验中相较于NB、OTNB、A2WNB、MAWNB算法的W值均为最高;相较于FTAWNB 算法在7 个数据集上获胜,1 个数据集上持平;相较于NB-LR 算法在7 个数据集上获胜;相较于HNB-LR 算法在8 个数据集上获胜。其可视化对比图如图6所示。 为了描述各权重参数对MAWOTFNB 算法分类性能的影响,本节对MAWOTFNB 算法的四个重要参数:类属性值权重Wd,类特定的联合离散属性值权重Wjkd,单个离散属性值权重Wj,aj以及联合离散属性权重Wjk展开研究。分别将这四个参数从MAWOTFNB 算法中删除来观察各部分权重在各数据集上对MAWOTFNB算法分类性能的影响。对应算法描述如下: 去除类属性值权重的MAWOTFNB算法,将该算法描述为A1; 去除类特定的联合离散属性值权重的MAWOTFNB算法,将该算法描述为A2; 去除单个离散属性值权重的MAWOTFNB算法,将该算法描述为A3; 去除联合离散属性权重的MAWOTFNB算法,将该算法描述为A4; 将四个权重参数全部去除的MAWOTFNB算法,将该算法描述为A5。 表8列出了各参数对比算法在每个数据集上的分类准确率。表9 展示了实验获得各参数对比算法在各数据集上的Fwa值。表8和表9中加粗的数字为该数据集上获得的最高分类准确率和Fwa值,本文将每个参数对比算法在10 个数据集上的平均分类准确率和平均Fwa值汇总在了表格底部。 表8 各参数对比算法在各数据集上的分类准确率Table 8 Classification accuracy of parameter comparison algorithms on each dataset 单位:% 表9 各参数对比算法在各数据集上的Fwa 值Table 9 Fwa values of parameter comparison algorithms on each dataset单位:% 为了分析各参数对比算法在各数据集中的分类效果,使用簇状柱形图可视化各参数对比算法的分类准确率、Fwa值,分别如图7、图8所示。分析结论如下: 图7 各参数对比算法在各数据集上的分类准确率对比Fig.7 Comparison of classification accuracy of parameter comparison algorithms on each dataset 图9 各参数对比算法的WDL值对比Fig.9 WDL value comparison of parameter comparison algorithms (1)算法A1是将类属性值权重去除的MAWOTFNB算法,该算法在训练时易受不平衡类的影响。由表8和表9 可知,其平均分类准确率和平均Fwa值相对于MAWOTFNB 算法分别低了9.92 个百分点和9.79 个百分点。因此,在算法训练时考虑训练数据集中类的平衡性是必要的。 (2)算法A2 是将类特定的联合离散属性值权重去除的MAWOTFNB算法,该算法在训练时没有对不同类中不同属性值之间的相关性进行衡量。由表8和表9可知,其平均分类准确率和平均Fwa值相对于MAWOTFNB算法分别低了9.28 个百分点和10.25 个百分点。因此,在算法训练时衡量不同类中的不同属性值之间的相关性可以大幅度提高算法的分类性能。 (3)算法A3 是将单个离散属性值权重去除的MAWOTFNB算法,该算法在训练时忽略了单个离散属性值对其所在样本所属类别的贡献程度。由表8和表9可知,其平均分类准确率和平均Fwa值相对于MAWOTFNB算法分别低了10.37 个百分点和9.66 个百分点。因此,在算法训练时考虑单个离散属性值对其所在样本所属类别的贡献程度可以有效地提高算法的分类性能。 (4)算法A4是将联合离散属性权重去除的MAWOTFNB算法,该算法在训练时将训练数据集中离散属性之间的相关程度默认为1。由表8 和表9 可知,其平均分类准确率和平均Fwa值相对于MAWOTFNB 算法分别低了9.86 个百分点和10.71 个百分点。因此,准确地衡量离散属性之间的相关程度可以有效提高算法的分类性能。 (5)算法A5 是将所有权重去除的MAWOTFNB 算法,该算法在训练时,针对离散属相互独立的假设,而针对连续属性则使用正交变换的方法来获取待分类样本的类条件概率。由表8 和表9 可知,其平均分类准确率和平均Fwa值相对于MAWOTFNB算法分别低了8.17个百分点和7.77个百分点。因此,使用多类属性加权和正交变换融合的方法来改进NB 算法,可以有效提高其分类性能。 为了进一步说明离散属性和离散属性值权重的重要性,本文对各参数对比算法在各数据集上的分类表现进行了对比,表10 展示了各参数对比算法在各数据集上所获得准确率的WDL。 表10 各参数对比算法的WDL值Table 10 WDL value of parameter comparison algorithms 由表10 可知,本文的MAWOTFNB 算法与其他去除权重参数的MAWOTFNB 算法相比,其W 值均为最高;相较于算法A1、A2、A5均在9个数据集上获胜,1个数据集上持平;相较于算法A3 和A4 在10 个数据集上均获胜。这充分证明了本文使用多类属性加权和正交变换方法改进NB 算法的有效性。其可视化对比图如 目前大多数削弱朴素贝叶斯算法的属性条件独立性假设的改进方法中,针对多维混合属性大多是将离散属性连续化或者连续属性离散化之后再进行下一步的改进。不同于已有的改进方法,本文提出了一种多类属性加权与正交变换融合的朴素贝叶斯改进算法,该算法首先对类属性值、离散属性和离散属性值进行加权,然后将加权后的离散属性及离散属性值加入到其条件概率计算公式中,最后融合基于连续属性正交变换改进的朴素贝叶斯算法,对后验概率进行计算,减小了不平衡数据集以及属性条件独立性假设对分类精度造成的负面影响。实验结果表明,该算法在处理多维混合属性的分类任务时可保留离散属性和连续属性内在信息,提高朴素贝叶斯算法的分类性能。此外,该算法在“Poor Students(实测)”数据集上的分类性能明显优于另外7种分类算法,这可以为各高校的贫困生判定工作提供决策参考。1.4 多类属性加权与正交变换的融合
2 实验与对比
2.1 缺失属性预处理

2.2 实验方法与数据

2.3 性能评价指标
2.4 算法时间复杂度分析



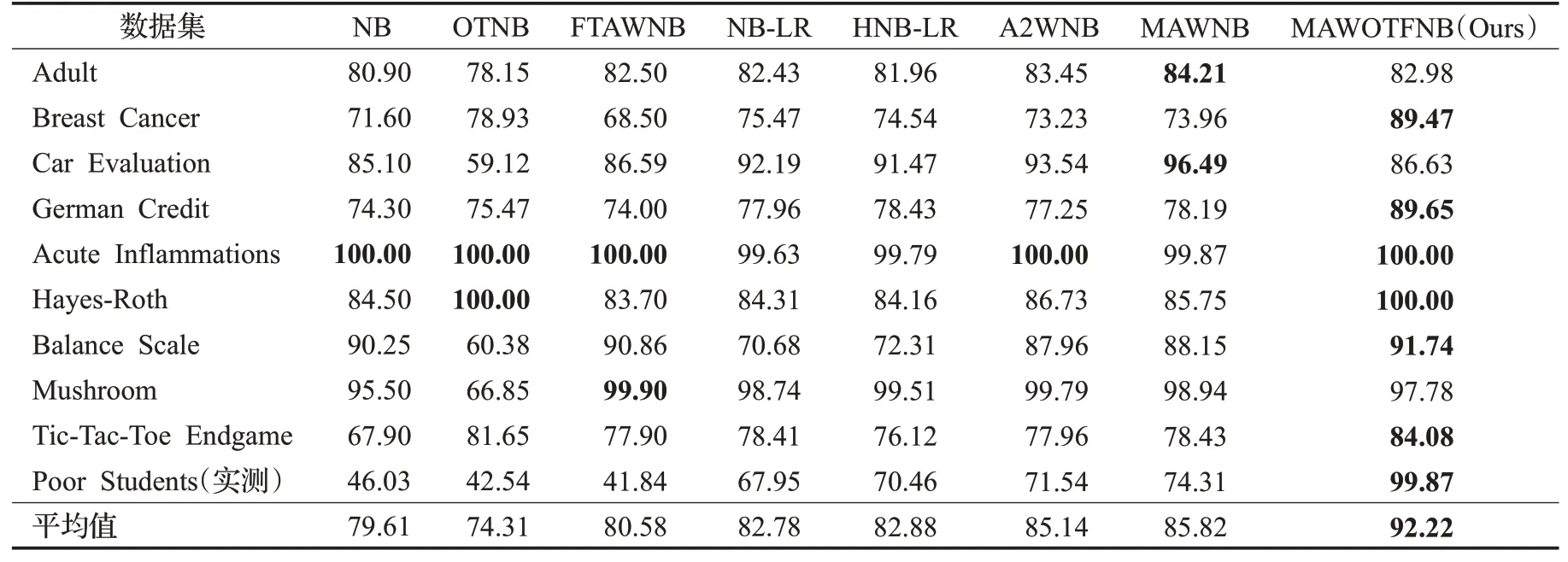
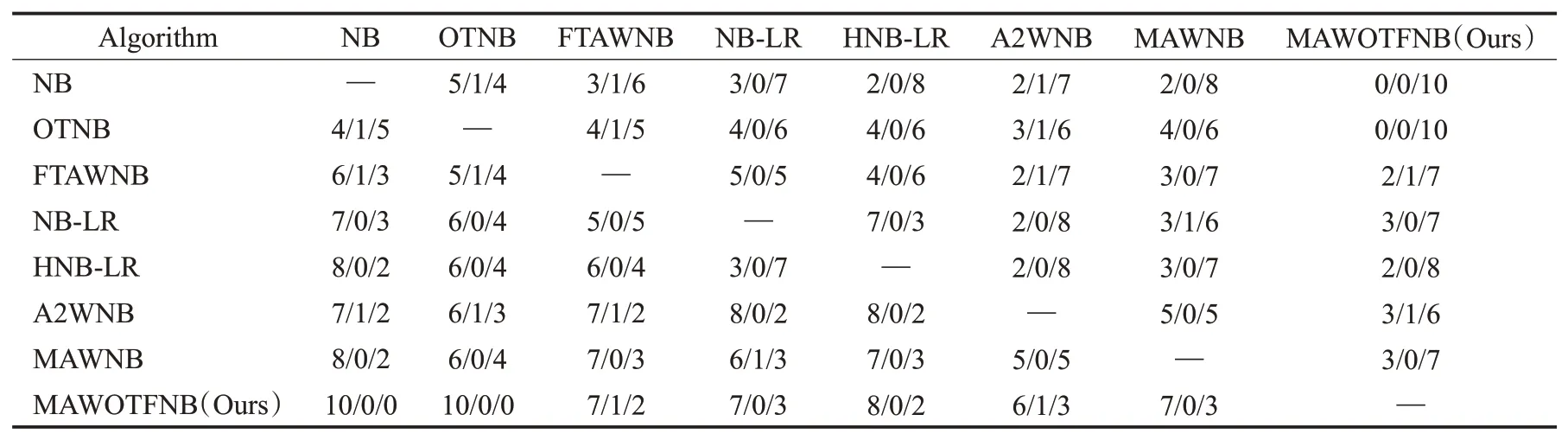
2.5 实验结果与分析




2.6 权重参数的影响





3 结束语

