高速同步电机临界转速下振动问题的维修

吴 勋

（西部管道乌鲁木齐应急抢险中心，新疆乌鲁木齐 830000）

0 引言

在西气东输三线一座天然气压气站，一台额定功率20 MW、额定电压10 000 V 的无刷励磁变频调速同步电机，额定转速4800 r/min，启停机过程中会经过2 个临界转速，分别为在1630 r/min 左右和2935 r/min 左右。在维修中更换电机驱动端滑动轴承后对电机空载运行测试，出现停机过程中降速通过二阶临界转速时振动测点②触发高高报警紧急停机，而启机过程无此问题。这时电机处于非正常状态。转子基本结构如图1 所示，振动传感器安装方式如图2 所示，测点②的电涡流振动传感器X 的振动值正常，Y 的振动趋势如图3 所示。

图1 转子结构

图2 振动传感器安装

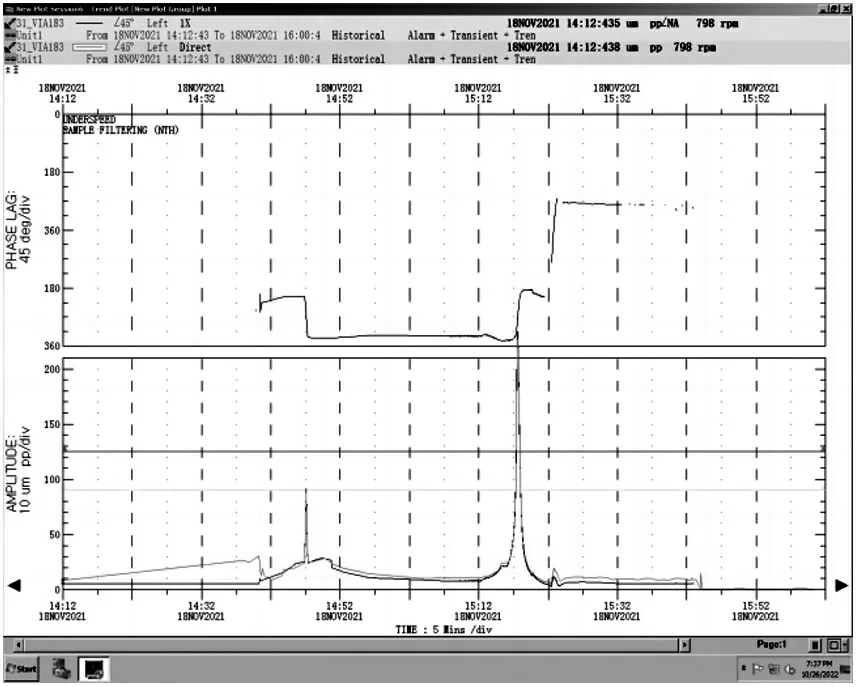
图3 Y 方向振动趋势

1 检查安装偏差

该同步电机和励磁机通过刚性联轴器连接，采用3 个水平剖分型滑动轴承支撑，轴承两侧有迷宫型润滑油封，安装要求的测量指标主要有4 项，现场检查和测量结果如表1 所示。

表1 现场安装情况检查

轴水平状态的变化反映了更换的①处轴承与原轴承厚度存在偏差。由于电机转子在线圈部位有重量集中，轴线产生挠曲，但挠曲很微小，可以按照线性估算如下：两处水平度需要调整0.12 mm/m，两处滑动轴承支撑距离为4 m，①处支撑需要降低（0.12/2）×4=0.24 mm。现场从轴承座底部减去0.20 mm 垫片后，重新测量轴水平，差值为-0.05 mm；同时测量抬升高度为1.66 mm，考虑①处降低后对③处轴承座抬升高度的影响，在③处轴承座底部增加0.05 mm 垫片。从安装角度完成调整后，启动电机运行，但降速通过二阶临界转速时振动值仍然高高报警触发联锁保护。

2 对异常振动问题的转子动力学分析

触发联锁保护的测点②Y 方向振动监测的图谱如图4 所示。从图4 中可以看到，停机过程中转速降低至第二阶临界转速附近时，振动值远大于升速过程相同转速下的振动值。

图4 测点②Y 方向振动伯德图

查阅文献，在一台50 MW 的发电机停机过程中也出现过降速通过二阶临界转速（3600 r/min）时振动显著增大的现象。通过转子动力学分析，与汽轮机连接的悬臂端占有超过78%的二阶振型动能，具有“balance pit”型振动形态的特征；经过平衡，消除这个现象。振动传感器监测的伯德图如图5 所示。

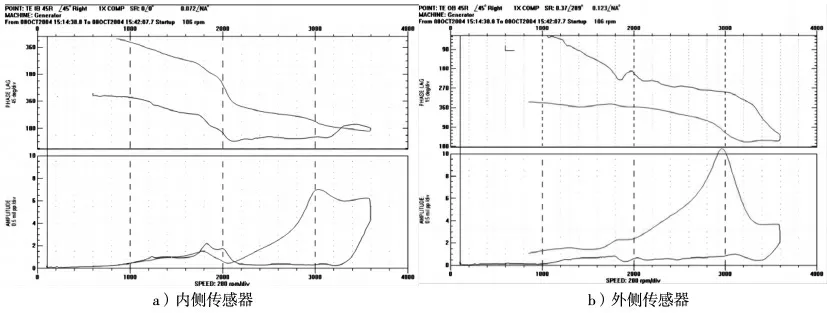
图5 文献中发电机升速和降速振动传感器伯德图

同步电机和励磁机的伯德图与参考文献中有差异，主要表现在振幅仅在临界转速处急剧增大，且降速通过二阶临界转速时振动通频值（direct）与基频（1X）几乎完全重合，振动幅值主要来源于基频；电机驱动端半联轴器的悬臂距离支撑点较近，悬臂现象并不十分显著。

3 现场对转子平衡状态的修正

对于单根转子，结构和支撑刚度、阻尼等条件确定后，会有自身的临界转速ncr1、ncr2、……；对于轴系，单根转子的临界转速会发生迁移，表现出新的临界转速Ncr1、Ncr2……。从启停机过程振幅与转速的变化关系来看，测点①在ncr1振幅有峰值，测点②和③在ncr2有峰值、且相位变化基本一致，测点②、③反映了励磁机转子的临界转速，而测点①反映了电机转子的临界转速。轴系表现出的二阶临界转速实际上是励磁机的一阶临界转速。

按照临界转速下振幅与激振力的相位关系，以及参考文献中对于挠性转子激振力超前最大振幅100°～130°和平衡槽加重时试加重相位=振幅最大值相位-240°的经验做法，在测点励磁机驱动端的旋转整流盘上安装试验重量15 g∠24°、15 g∠36°（由于旋转整流盘上平衡孔沿圆周均布30 个，相邻两个间隔12°），试验重量安装前后的振动变化见表2。

表2 增加试重后最大振幅附近振动值变化

对励磁机一阶振型的平衡计算采用振型圆法，运用CAD 可以方便地绘制矢量、拟合圆，减少矢量计算和矩阵计算的工作量。基于CAD 绘制的振型圆如图6 所示。

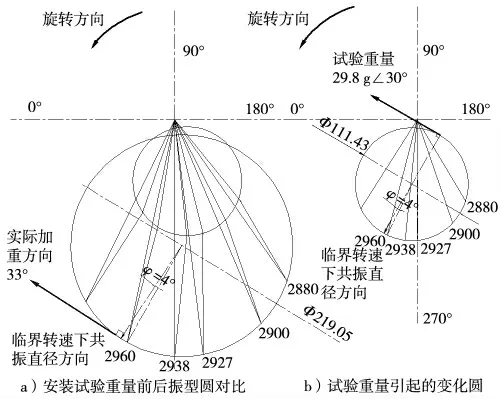
图6 基于CAD 绘制的振型圆

图中角度φ从图6b）中确定，试验重量的相位已知，与相位方向垂直即为临界转速方向，φ为ncr与邻近转速n0在圆上的圆心角，如n0超前ncr，在初始振型圆上n0的方向滞后角度φ得到该阶振型临界转速方向，进而确定激振力和实际加重的相位。

加重量计算公式与影响系数法类似，但模与相位角分别确定。实际加重W=（O′A/O′C）×w=（219.05/111.43）×29.8=58.6 g；角度33°；在24°处加重30.6 g，在36°处加重28.1 g。电机降速过二阶临界转速的振动值降为76 μm，额定转速的振动值为18 μm，共振放大系数为76/18=4.2，符合共振放大系数3～5 的要求。同时可以看出，试验重量安装后，极坐标图中最大振幅的相位变化不大，说明试验重量的位置选择是正确的，计算后也得到证实。

4 对振型圆法应用的回顾

设Z 方向沿转轴、M 为质量、C 为外部阻尼、K 为刚度、Q 为不平衡复向量，从形如下式的转子运动微分方程：

从微分方程可以推导出，当转子接近某一临界转速时，得到形如以下方程的解：

该方程为圆方程，转速在i 阶临界转速附近，相位也会发生较大变化（通常跃变约90°）幅相特性曲线可以拟合为圆。对于轴系，受其他阶次振型的干扰等影响，超前最大振幅对应相位90°并非该阶振型真实激振力的方向。

振型圆法基本思路为：从幅相曲线拟合某一临界转速附近振幅矢量，得到该阶临界转速引起的振型圆，设直径为，加试验重量w∠α 后，得到新的幅相曲线，同样拟合找出该阶临界转速引起的振型圆图形；两个图上对应转速的矢量差即为试验重量引起的变化。

式（2）中，a1、b1和Cis均∝Ω/ωr，其中Ω 在Ωcr±δΩ 范围内。在试验重量添加前后式（2）可写作：

5 结束语

设图6b）中某一转速对应的圆心角为γ，图6a）中对应的圆心角为α，由计算可知，α-γ=arccos［M1/（2M2）］。临界转速与邻近转速对应的圆心角相等。

拟合振型圆的转速应与临界转速接近，不同的转速间隔选择，拟合的振型圆直径和试验重量引起变化的圆略有偏差，但试验配重偏差一般不超过15%，相位偏差不超过10°，同样可以获得较好的平衡效果。画出试验重量安装前后的振型圆后，也可以利用振型圆谐分量法的计算结果，试验重量引起的影响因子为幅相曲线上原点O 与两个振型圆上最大振幅点连线的截距矢量；对于一阶振型对称加重

对一次高压同步电机轴系出现二阶振动高高报警联锁保护问题的维修处理，发现安装的偏差的影响并不显著，主要由滑动轴承的阻尼和刚度等特性变化引起，并应用振型圆法对转子平衡状态进行修正，消除了异常振动的问题；并论述了振型圆法的原理，在运行转速在临界转速以上的挠性转子中可以应用。