基于光谱变换的滨海湿地土壤全氮含量建模预测①

张清文，吴风华，宋敬茹，汪金花，张永彬，刘明月,2,3,4，李孟倩，李春景，郝玉峰，满卫东,2,3,4*

基于光谱变换的滨海湿地土壤全氮含量建模预测①

张清文1，吴风华1，宋敬茹1，汪金花1，张永彬1，刘明月1,2,3,4，李孟倩1，李春景5，郝玉峰6，满卫东1,2,3,4*

(1 华北理工大学矿业工程学院，河北唐山 063210；2 唐山市资源与环境遥感重点实验室，河北唐山 063210；3 河北省矿区生态修复产业技术研究院，河北唐山 063210；4 矿产资源绿色开发与生态修复协同创新中心，河北唐山 063210；5延边大学地理与海洋科学学院，吉林延吉 133002；6 河北省地质矿产勘查开发局第八地质大队，河北秦皇岛 066001)

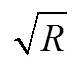
光谱变换；土壤全氮含量；偏最小二乘回归；随机森林回归；支持向量机回归

氮元素是土壤中最大的限制性营养元素，在动植物生长、微生物呼吸中有着不可或缺的作用[1]。土壤全氮(TN)含量的高低直接影响滨海湿地生态系统的初级生产力，且对生态系统碳循环等其他生物化学循环有重要影响[2]。滨海湿地是陆地生态系统和海洋生态系统的缓冲区，在净化水体、涵养水源和保持生物多样性等方面有重要作用[3]，同时也是全球气候变化和人类活动共同作用下的生态敏感区，生态脆弱性高。人类生产生活排放已经造成滨海湿地氮循环失衡[4]，所以准确预测土壤TN含量对生态系统氮循环有重要意义。

传统化学分析方法测定土壤TN含量精度较高，但劳动强度大，人力财力消耗多，且产生大量环境污染[5]。高光谱技术的发展为实现快速、简便、无污染估测土壤各种理化性质提供了新的方法。很多学者通过对原始光谱进行变换、计算光谱指数、筛选敏感波段等方法确定自变量，再基于数学模型对土壤各种理化性质进行估测，如土壤含水量[6]、重金属含量[7]、有机质含量[8]、有机碳含量[9]等，均达到了较好的预测效果。高光谱所含土壤信息丰富，合理选取建模波段对土壤TN含量的准确预测极其重要。刘凡等[10]利用677 nm和1 414 nm波段反射率建立了土壤TN含量模型，但2个波段难以概括全部土壤信息，所建模型有一定的局限性。李焱等[11]选取Pearson相关系数最大的10个波段与土壤TN含量进行建模分析，建模效果得到一定程度的改进。于雷等[12]比较了全波段建模与敏感波段建模，发现虽然基于全波段建模精度要优于敏感波段，但敏感波段建立的模型复杂度远远低于全波段建模。为了包含绝大部分光谱信息，同时尽量降低模型复杂度，筛选敏感波段是必要的。

目前，用于估测土壤理化性质的线性模型有多元线性回归、多元逐步回归和偏最小二乘回归(Partial Least Square Regression，PLSR)等[13-14]。其中，多元线性回归适用于自变量少，且自变量之间相关性较小的情况，对于土壤光谱，波段数较多且波段之间相关性强，所以多元线性回归有一定的局限性[15]；多元逐步回归可以筛除干扰变量，选择合适的解释变量回归，但是依然不能解决波段间的共线性问题；而PLSR通过提取主成分的方法可以解决这一问题，且可以实现对全部波段信息的概括，建模效果优于多元线性回归和多元逐步回归[16]。除此之外，机器学习算法中如决策树回归、随机森林回归(Random Forest Regression，RFR)和支持向量机回归(Support Vector Regression，SVR)等具有极强的非线性拟合能力，被广泛应用于土壤性质的估算[17]。决策树回归复杂度低且适用于高维数据，是构建非线性模型的常用方法，但单棵决策树回归容易过拟合，泛化能力差。RFR由多棵决策树集成，改善了单棵决策树的缺点，更加稳定，是高光谱估测土壤理化性质的理想方法[18]。除机器学习外，深度学习也被广泛应用，有学者比较了RFR、SVR和神经网络建模，结果表明RFR优于神经网络和SVR[19]。

滨海湿地土壤受潮汐影响大，海水携带的营养物质多，理化性质更新快，湿地土壤TN含量与内地差异较大。由于野外采样受涨潮影响，采样可达性差，所以基于原始光谱及其多种光谱变换形式的滨海湿地土壤TN含量建模研究较少。基于此，本研究通过PLSR、RFR和SVR三种建模方法结合不同光谱变换构建土壤TN含量的预测模型，分析模型效果优劣，探求可用于滨海湿地土壤TN含量的光谱预测方法，以期为估测滨海湿地土壤TN储量提供方法依据，同时为揭示滨海湿地生态系统氮循环提供帮助。

1 材料与方法

1.1 土样的采集与制备

采用环刀法采集133个唐山市和秦皇岛市滨海湿地表层土样(采样深度为0 ～ 20 cm)，采样点分布如图1所示。为减少外界因素对样品TN含量的影响，对所采集的土样进行室内自然风干，剔除异物，碾磨，过100目筛，然后分为2份，分别用于凯氏蒸馏法测定土样TN含量[20]和高光谱数据采集。

土壤TN含量统计特征如表1所示。土壤TN含量最大值为3.124 g/kg，采集于芦苇湿地；TN含量最小值为0.024 g/kg，采集于海边砂土；TN平均含量为0.733 g/kg，标准差为0.501 g/kg，变异系数为68.5%。133个土样中包含84个粉土和49个砂土，不同质地的土样土壤TN含量平均值有显著差异，粉土TN含量平均值为0.881 g/kg，砂土TN含量平均值为0.478 g/kg。砂粒含量较高的土样TN含量低，粉粒含量高的土样TN含量高[21]。

1.2 土样光谱测定与预处理

(该图基于国家测绘地理信息局标准地图服务网站下载的审图号为 GS(2020)4619 的标准地图制作，底图无修改)

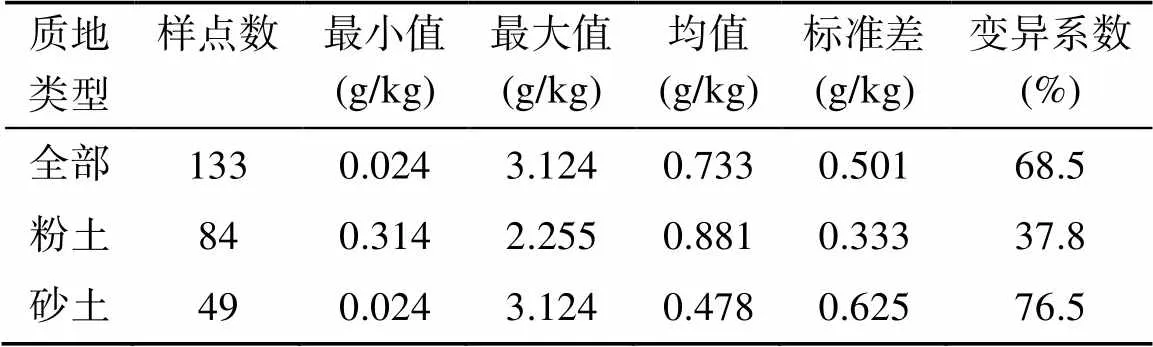
表1 土壤质地及其TN含量描述性统计特征

本研究对土壤TN含量与光谱反射率及其各种变换形式进行相关性分析，Pearson相关系数范围为–1.0 ～ 1.0，绝对值越大，其相关性越高，波段越敏感；选取相关系数大于0.4的波段，进行<0.01水平上的显著性检验，通过显著性检验的波段确定为敏感波段，用于土壤TN含量高光谱模型的估算。

1.3 数据分析方法

1.3.1 偏最小二乘回归(PLSR) PLSR兼顾了多元线性回归、主成分分析和自变量因变量相关性分析3种分析方法的优点，不仅能解决自变量相关性较强的问题，还可以通过提取主成分的方式降低自变量维数，在样本数远小于自变量数的情况下建模。本研究通过判断留一法(leave One Out，LOO)交叉验证的预测均方根误差(Root Mean Square Error of Prediction，RMSEP)确定主因子个数。理想的RMSEP值随主因子个数的增加先递减，达到最低点后随主因子个数的增加出现微小上升或波动。取RMSEP最小时对应的主因子个数建立PLSR模型可有效避免过拟合问题。本研究选择与土壤TN含量相关性强的成分，不考虑全部的自变量，因此建立的模型有更好的鲁棒性。采用R软件中“pls”包完成PLSR建模。

1.3.2 随机森林回归(RFR) RFR是多个决策树集成的学习器，可以高精度地处理大数据集，具有数据适应性强、不易受极大值或极小值的影响即稳定性高等优点，所以模型稳定性比PLSR高。RFR通过对多个决策树的集成融合，输出结果为多棵决策树的平均值。构建RFR模型：

1.3.3 支持向量机回归(SVR) SVR是一种基于统计学习理论的机器学习技术。SVR使用核函数将数据投影到高维空间，并进行回归。在SVR建模中，选取径向核函数，调整两个参数gamma和cost。其中，cost为惩罚系数，cost过大，容易出现过拟合，cost过小，容易拟合不充分；gamma决定数据映射到高维空间后的分布，gamma越大，支持向量越少，gamma值越小，支持向量越多。本研究利用“caret”包的网格搜索法确定最优参数gamma和cost，采用预测误差最小的参数组合进行最终建模。使用R软件“e1071”包建立SVR模型。

1.3.4 模型精度验证 建立土壤TN预测模型，采用LOO交叉验证。模型的评价指标采用预测值与实测值的决定系数(2)、均方根误差(Root Mean Squared Error，RMSE)和平均绝对误差(Mean Absolute Error，MAE)。其中，RMSE用来衡量观测值同真值之间的偏差；MAE是绝对误差的平均值，能更好地反映预测值误差的实际情况。模型精度评价标准如表2所示，2越接近1，拟合效果越好，RMSE、MAE值越小，说明模型估算精度越高。计算公式为：

表2 模型整体精度评价标准[24]

2 结果与分析

2.1 土壤光谱特征和全氮含量的相关性

由图2可以看出，研究区土壤样本的原始光谱反射率()曲线形态基本一致，各曲线间差异较小，呈曲折上升的弧形，在1 410、1 920、2 210 nm出现3个明显的水分吸收谷。其中，在可见光波段(350 ～ 780 nm)范围内，迅速上升；除吸收谷外，在近红外波段780 ～ 1 900 nm范围内缓慢上升，各样本光谱间差异较大，至2 100 nm处达到最大值；在近红外波段2 150 ～ 2 500 nm范围内，平缓下降。结合野外采样点，砂土样品的曲线在2 300 ～ 2 400 nm处出现明显吸收谷，此区间是硅酸盐矿物中的水分子羟基(–OH)伸缩振动的合频谱带，由于砂土中硅酸盐矿物含量较大[25]，所以在图2中砂土样品的反射率曲线在2 300 ～ 2 400 nm出现明显吸收谷，与粉土样品曲线出现交叉现象。

图 2 供试土壤样本原始光谱反射率

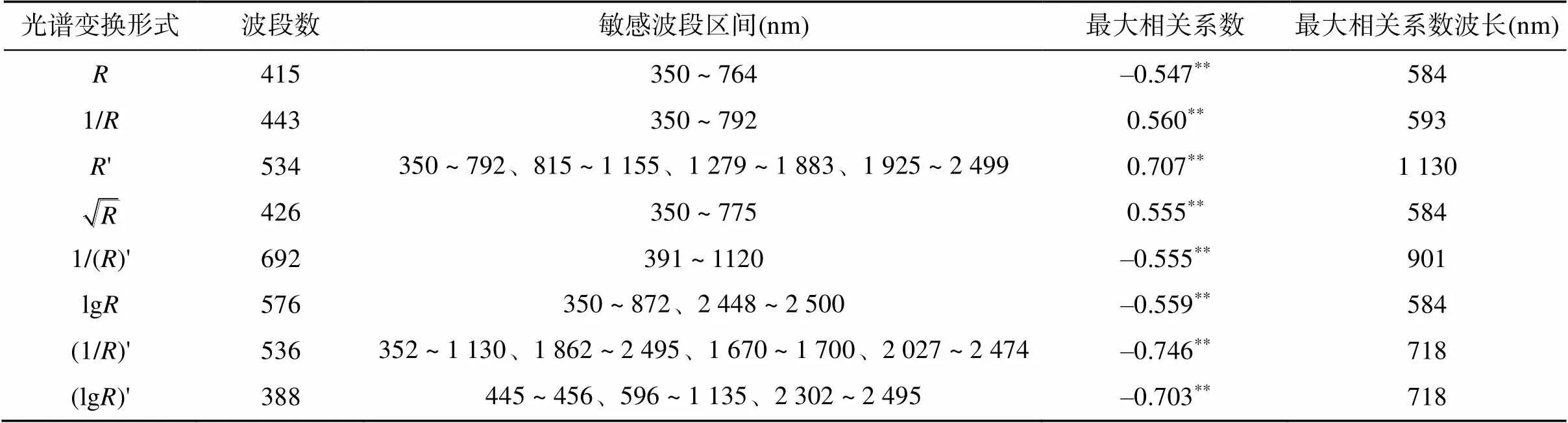
表3 不同变换形式下土壤TN含量与光谱波段的相关性

注：*、**分别表示在<0.05和<0.01水平显著相关。

2.2 模型对比分析

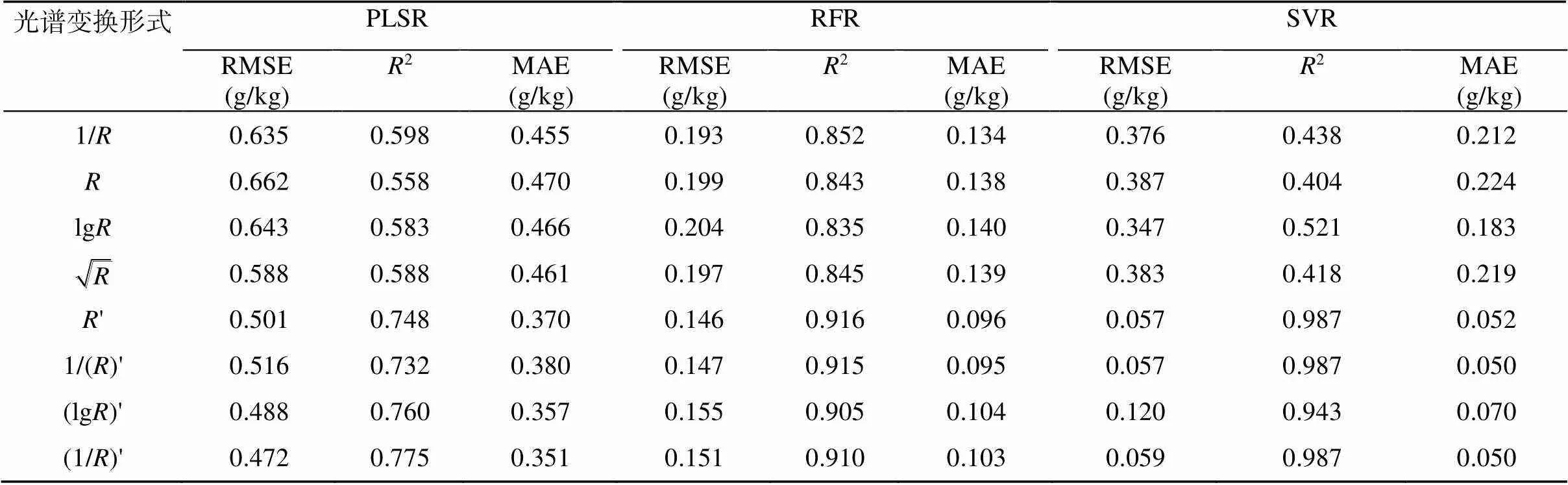
表4 各预测模型的验证与对比

对进行7种光谱变换之后，建模2、RMSE和MAE得到了改善，但不同变换形式所建模型精度差异较大。和'、1/和(1/)'、lg和(lg)'相比，一阶微分变换参数建模效果显著优于未经过一阶微分变换参数。经一阶微分变换，反射率大小与土壤TN含量之间的关系转化为反射率斜率与土壤TN含量之间的关系，消除了反射率大小中的噪声，所以一阶微分变换参数建模的效果普遍较好。和1/、'和1/'在3种建模方法中表现相近，说明经简单的倒数运算对光谱信息的挖掘能力较弱。Brunet等[30]、徐永明等[31]也比较了基于微分变换与其他光谱变换所建立的预测模型精度，结果证明，一阶微分变换所建模型精度更高。因此，对进行合适的光谱变换，对于提高土壤TN含量预测模型的精度和稳定性具有关键作用。

本研究选取敏感波段为自变量，以土壤TN含量为因变量进行PLSR、RFR和SVR，建立及其7种光谱变换形式对土壤TN含量的预测模型。图3显示了3种回归方法各自的最优模型的土壤TN含量预测值与实测值的散点图，可以明显看出，SVR模型预测的土壤TN含量与实测值的拟合曲线比PLSR和RFR模型更接近1∶1线，表明实测值与预测值较为接近，模型预测精度更高。

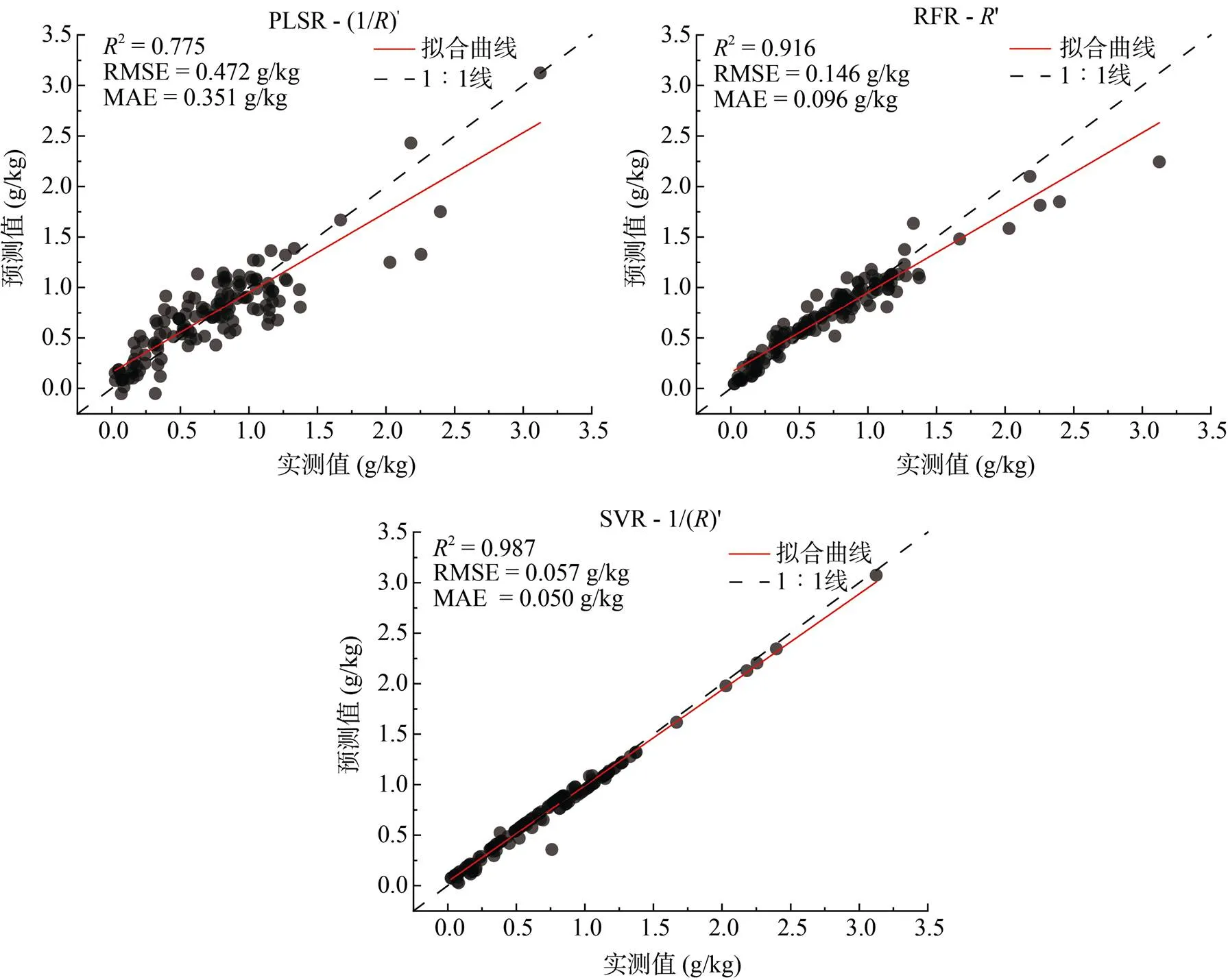
图3 PLSR、RFR、SVR建模中最优模型土壤TN含量实测值与预测值比较

3 结论

1) 滨海湿地土壤原始光谱反射率与TN含量有较好的相关性，可以用于对土壤TN含量进行估测，而对原始光谱反射率曲线进行变换，可进一步提高光谱反射率与土壤TN含量的相关性，其中提高最明显的变换形式为(1/)'。微分变换可以有效消除噪音，提高光谱反射率对土壤全氮含量的敏感度，故利用土壤光谱反射率预测土壤TN含量是可行的。

2) 根据光谱反射率及其变换形式建立的PLSR、RFR和SVR模型，每种算法里均有较好的预测模型可以粗略预测土壤TN含量。在PLSR模型中，基于(1/)' 建立的模型预测精度最高，可以粗略预测土壤TN含量；在RFR模型中，基于' 建立的模型可精确预测土壤TN含量；在SVR模型中，基于1/()'建立的模型可准确预测土壤TN含量。在建立的模型中，经光谱变换后建立的模型预测精度比基于建立的模型精度有所提升，故对变换后建模是科学的。

3) 基于1/()'建立的SVR模型2为0.987，RMSE为0.057 g/kg，MAE为0.050 g/kg，是预测滨海湿地土壤TN含量的最优模型。

[1] 王莉雯, 卫亚星. 植被氮素浓度高光谱遥感反演研究进展[J]. 光谱学与光谱分析, 2013, 33(10): 2823–2827.

[2] 宋长春, 宋艳宇, 王宪伟, 等. 气候变化下湿地生态系统碳、氮循环研究进展[J]. 湿地科学, 2018, 16(3): 424–431.

[3] Kirwan M L, Megonigal J P. Tidal wetland stability in the face of human impacts and sea-level rise[J]. Nature, 2013, 504(7478): 53–60.

[4] Socolow R. Fitting on the earth: Challenges of carbon and nitrogen cycle to preserve the habitability of the planet[J]. Engineering, 2016, 2(1): 21–22.

[5] 王红, 刘高焕, 宫鹏. 利用Cokriging提高估算土壤盐离子浓度分布的精度——以黄河三角洲为例[J]. 地理学报, 2005, 60(3): 511–518.

[6] 刘焕军, 王翔, 张小康, 等. 松嫩平原主要土壤类型含水量高光谱预测模型[J]. 土壤通报, 2018, 49(1): 38–44.

[7] 郭云开, 张思爱, 王建军, 等. 特征变量选择结合SVM的耕地土壤Hg含量高光谱反演[J]. 测绘工程, 2022, 31(1): 17–23.

[8] 勾宇轩, 赵云泽, 李勇, 等. 基于CWT-sCARS的东北旱作农田土壤有机质高光谱反演[J]. 农业机械学报, 2022, 53(3): 331–337.

[9] 陈秋宇, 杨仁敏, 朱长明. 基于VIS-NIR光谱的互花米草入侵湿地土壤有机碳预测研究[J]. 土壤学报, 2021, 58(3): 694–703.

[10] 刘凡, 马玲, 杨光, 等. 灰漠土土壤全氮含量的高光谱特征分析及估测[J]. 新疆农业科学, 2017, 54(1): 140–147.

[11] 李焱, 王让会, 管延龙, 等. 基于高光谱反射特性的土壤全氮含量预测分析[J]. 遥感技术与应用, 2017, 32(1): 173–179.

[12] 于雷, 洪永胜, 耿雷, 等. 基于偏最小二乘回归的土壤有机质含量高光谱估算[J]. 农业工程学报, 2015, 31(14): 103–109.

[13] 涂宇龙, 邹滨, 姜晓璐, 等. 矿区土壤Cu含量高光谱反演建模[J]. 光谱学与光谱分析, 2018, 38(2): 575–581.

[14] 尼加提·卡斯木, 师庆东, 郭玉川, 等. 基于EM38和WorldView-2影像的土壤盐渍化建模研究[J]. 土壤, 2019, 51(3): 594–601.

[15] 钱佳, 郭云开, 蒋明, 等. 不同类型土壤Cu含量高光谱联合反演建模[J]. 测绘科学, 2020, 45(8): 138–144.

[16] 陈红艳, 赵庚星, 李玉环, 等. 消除水分因素影响的野外原状土壤盐分高光谱建模估测[J]. 农业工程学报, 2018, 34(12): 119–125.

[17] 张东辉, 赵英俊, 秦凯. 一种新的光谱参量预测黑土养分含量模型[J]. 光谱学与光谱分析, 2018, 38(9): 2932–2936.

[18] 王腾军, 方珂, 杨耘, 等. 随机森林回归模型用于土壤重金属含量多光谱遥感反演[J]. 测绘通报, 2021(11): 92–95.

[19] Cui L J, Dou Z G, Liu Z J, et al. Hyperspectral inversion ofcarbon, nitrogen, and phosphorus stoichiometry using three models[J]. Remote Sensing, 2020, 12(12): 1998.

[20] 鲍士旦. 土壤农化分析[M]. 3版. 北京: 中国农业出版社, 2000.

[21] 林俊杰, 杨振宇, 刘丹, 等. 干湿交替下三峡支流消落带沉积物粒径组成及氮分布特征[J]. 土壤学报, 2016, 53(3): 602–611.

[22] 孙兴亮, 郝晓华, 王建, 等. 基于光谱-环境随机森林回归模型的MODIS积雪面积比例反演研究[J]. 冰川冻土, 2022, 44(1): 147–158.

[23] Song J R, Gao J H, Zhang Y B, et al. Estimation of soil organic carbon content in coastal wetlands with measured VIS-NIR spectroscopy using optimized support vector machines and random forests[J]. Remote Sensing, 2022, 14(17): 4372.

[24] Viscarra Rossel R A, McGlynn R N, McBratney A B. Determining the composition of mineral-organic mixes using UV-vis-NIR diffuse reflectance spectroscopy[J]. Geoderma, 2006, 137(1/2): 70–82.

[25] 王惠敏. 基于光谱吸收特征的土壤有机质与重金属含量估算研究[D]. 徐州: 中国矿业大学, 2019.

[26] 殷哲, 雷廷武, 陈展鹏, 等. 近红外传感器测量不同种类土壤含水率的适应性研究[J]. 农业机械学报, 2014, 45(3): 148–151, 190.

[27] 殷彩云, 白子金, 罗德芳, 等. 基于高光谱数据的土壤全氮含量估测模型对比研究[J]. 中国土壤与肥料, 2022(1): 9–15.

[28] 王海江, 刘凡, Yunger J A, 等. 不同粒径处理的土壤全氮含量高光谱特征拟合模型[J]. 农业机械学报, 2019, 50(2): 195–204.

[29] 徐彬彬. 土壤剖面的反射光谱研究[J]. 土壤, 2000, 32(6): 281–287.

[30] Brunet D, Barthès B G, Chotte J L, et al. Determination of carbon and nitrogen contents in Alfisols, Oxisols and Ultisols from Africa and Brazil using NIRS analysis: Effects of sample grinding and set heterogeneity[J]. Geoderma, 2007, 139(1/2): 106–117.

[31] 徐永明, 蔺启忠, 黄秀华, 等. 利用可见光/近红外反射光谱估算土壤总氮含量的实验研究[J]. 地理与地理信息科学, 2005, 21(1): 19–22.

Estimating of Soil Total Nitrogen Content in Coastal Wetland Based on Spectral Transformation

ZHANG Qingwen1, WU Fenghua1, SONG Jingru1, WANG Jinhua1, ZHANG Yongbin1, LIU Mingyue1, 2, 3, 4, LI Mengqian1, LI Chunjing5, HAO Yufeng6, MAN Weidong1, 2, 3, 4*

(1 College of Mining Engineering, North China University of Science and Technology, Tangshan, Hebei 063210, China;2 Tangshan Key Laboratory of Resources and Environmental Remote Sensing, Tangshan, Hebei 063210, China; 3 Hebei Industrial Technology Institute of Mine Ecological Remediation, Tangshan, Hebei 063210, China; 4 Collaborative Innovation Center of Green Development and Ecological Restoration of Mineral Resources, Tangshan, Hebei 063210, China; 5 College of Geography and Ocean Sciences, Yanbian University, Yanji, Jilin 133002, China; 6 The 8thGeological Brigade of Hebei Bureau of Geology and Mineral Resource Exploration, Qinhuangdao, Hebei 066001, China)

Spectral transformation; Soil total nitrogen content; Partial least squares regression; Random forest regression; Support vector regression

S151.9

A

10.13758/j.cnki.tr.2023.04.022

张清文, 吴风华, 宋敬茹, 等. 基于光谱变换的滨海湿地土壤全氮含量建模预测. 土壤, 2023, 55(4): 880–886.

国家自然科学基金项目(41901375，42101393)和河北省自然科学基金项目(D2022209005)资助。

(manwd@ncst.edu.cn)

张清文(1998—)，男，山东临沂人，硕士研究生，主要从事生态环境遥感研究。E-mail：zhangqingwen@stu.ncst.edu.cn