基于声学单元动水压力作用下的进水塔损伤特性分析

郑晓东，沈一鸣，阮浩东，赵逸博，徐世界

（1. 河北工程大学水利水电学院，河北 邯郸 056001； 2. 河北工程大学 河北省智慧水利重点实验室，河北 邯郸 056038）

0 引 言

进水塔一般是独立于水库中的高耸空腹矩形钢筋混凝土结构，塔体内外长期有不超过塔体高度的流动水体。由于进水塔塔体高宽比较大，塔体的抗弯强度相对较柔，其主要受风、地震等横向荷载的作用。在地震作用下，动水压力对塔体的动力响应不可忽视，因此，库水-塔体之间的耦联振动问题一直是水利工程中动力分析的一个重要课题。

目前，诸多学者主要通过不可压缩的附加质量模型研究此类耦联振动问题。虽然该模型能够比较好地模拟库水-塔体的相互作用，反映出动水压力的本质特征，但是附加质量法没有考虑库水的压缩性和塔体的弹性变形，这是与实际不相符的，从而不能真实反映库水-塔体之间的耦联振动问题。水与地基［1-3］、地基与结构［4-6］存在复杂的相互作用，很多学者通过不同方法建立结构-流体-地基模型，将三者看成有机统一体进行分析。张博［7］、党康宁［8］对进水塔分别采用流固耦合和附加质量方法进行了对比，提出附加质量模型不能充分考虑动水压力对于进水塔复杂结构的影响；王铭明等［9］以重力坝为模型，建立坝体-库水系统模型实验，并将结果与流固耦合模型和附加质量模型比较，结论表明附加质量模型夸大水体对结构的动力响应；邱奕翔［10］等基于结构自振频率分析，讨论了附加质量模型与流固耦合模型（可、不可压缩）性对坝体动力特性的影响；张汉云［11］等基于势流体理论分析了不同边界条件下动水压力的分布规律及动力响应分析，但并未对进水塔进行损伤特性分析，不能充分体现动水压力的影响；赵秋红［12］、许贺［13］详细分析了水与结构的耦合作用机理和分析方法，比较了不同规范中计算动水压力的方法及存在的不足；高立宝等［14］对比研究了不同规范中地震动附加动水质量的差异性和计算精度，结论表明不同规范间的附加质量模型动水压力值存在差异；李艳朋［15，16］等研究基于声固耦合法的拱坝-库水-地基相互作用分析，研究拱坝库底吸收边界对坝面动水压力分布及坝体动力响应的影响；WANG［17］、王丕光［18］等针对结构动水压力进行了深入分析，库水压缩性对结构动水压力分布影响较大不可忽略。

本文采用ABAQUS 中的声学单元模拟具有可压缩性的库水［19］，建立进水塔-库水-地基三维有限元模型，分析声学单元模型下进水塔的动力响应、动水压力分布规律、损伤特性的影响。该方法对库水-塔体-地基进行更为真实的仿真，可为进水塔耦联振动问题的研究提供参考。

1 声固耦合法运动方程的建立

考虑到进水塔—库水—地基的耦联震动作用，将库水视为可压缩声学介质的理想流体，设声学介质坐标为（x，y，z），质点运动位移为（u，v，w），根据牛顿定律可得［16］：

其中P为动水压力，可以表示为：

其中K为体积弹性模量，可以表示为。

联立式（1）、（2），得到以动水压力P为目标函数的波动方程：

其中C为水中的声波波速，可以表示为。

为求得波动方程的解，还需要给出声固耦合模型的边界条件分别为：库水表面条件、进水塔—库水耦合边界条件、地基—库水接触边界条件、边界辐射条件，如图1所示。

图1 进水塔—库水—地基相互作用及边界条件示意图Fig.1 Diagram of interaction and boundary conditions of intake tower-reservoir water-foundation

库水自由表面应满足：

进水塔—库水耦合边界条件应满足：

在地基—库水接触时，需考虑库底边界的吸收效应，则边界条件应满足：

在库水截断处的辐射条件应满足：

式中：n为库水截断边界内法向；θ为与内法向之间的入射角［21］。

2 有限元模型及计算参数

2.1 进水塔有限元模型

选取我国西南羊曲水电站进水塔为主要研究结构，建立进水塔-库水-地基有限元计算模型，该塔体高度为85.5 m，正常蓄水位深74 m，塔座材料采用C30 混凝土，塔体采用C25 混凝土，进水塔采用C3D8R模拟，单元总数为32 445 个，采用混凝土损伤模型（CDP），地基采用C3D8R 单元模拟，单元总数为7 776个。水体采用声学单元AC3D8 模拟，单元总数：5 950 个。库水的密度为1 000 kg/m³，库水体积模量取为2 GPa（水体可压缩）［10］。详细材料参数见表1。

表1 进水塔各部位结构材料参数取值Tab.1 Structural material parameter values of each part of the water intake tower

库水表面设置为自由表面，库水截断边界处设置为吸收边界，使动水压力波不会在尾部产生回弹波，用以模拟辐射阻尼作用，从而真实反应动水压力对进水塔的影响；在进水塔—库水、地基—库水的接触面采用Tie 约束用来模拟声学介质与结构之间的耦合作用。

整体三维有限元模型及进水塔有限元模型如图2所示。根据《水工建筑物抗震设计标准》（GB51247-2018），塔身大体积混凝土的动态弹性模量较静态弹性模量提高50%，动力计算时阻尼比取7%。

2.2 地震波的选取

羊曲水电站为一等大（1）型工程，泄洪洞进水塔建筑物级别为1 级。泄洪洞进水塔工程抗震设防类别为甲类，地震基本烈度为7级，设防烈度为8级。泄洪洞进水塔按1级挡水建筑物设计，取基准期100年超越概率P100=2%的地震动参数作为设计地震，相应基岩水平地震动峰值加速度为0.304g，特征周期Tg=0.2 s；设计反应谱最大值βmax=6.71。根据抗震设计反应谱的建议拟合出地震人工波：总时长20 s，时间步长为0.01 s，如图3所示。

图3 设计人工地震波Fig.3 Design of artificial seismic waves

3 结果与分析

3.1 模态分析

图4 为不同动水模型下进水塔的自振频率曲线。由图4 可知，声学单元模型的每一阶自振频率均高于附加质量模型，这是由于结构自振频率大小与结构质量成反比，附加质量模型是将动水压力通过公式转换为结点质量，直接加到节点导致模型质量增加，从而导致进水塔自振频率有所减小，而声学单元模型是通过定义声学单元模拟可压缩的水体与结构相互作用面实现的，施加方法更加符合真实水体存在的方式。

3.2 动水压力分析

图5 为进水塔各迎水面的动水压力对比图，主要通过提取进水塔顺水流方向和垂直水流方向进水塔的动水压力进行分析。由图5 可知，声学单元模型模拟的在垂直进水塔水流方向上的动水压力值最大，顺水流方向的进水塔正面的动水压力值其次，背部动水压力值最小。声学单元模型在进水塔外部各个迎水面的动水压力分布规律大体一致，外包络线呈现抛物线的分布规律，在水面处的动水压力基本为0，随着水深的增加动水压力也相应增加；附加质量模型的动水压力曲线并不是规律的曲线，这是因为在附加质量法在计算动水压力时，考虑到塔体变形和加速度分布的影响，即沿进水塔高度方向加速度是变化的。

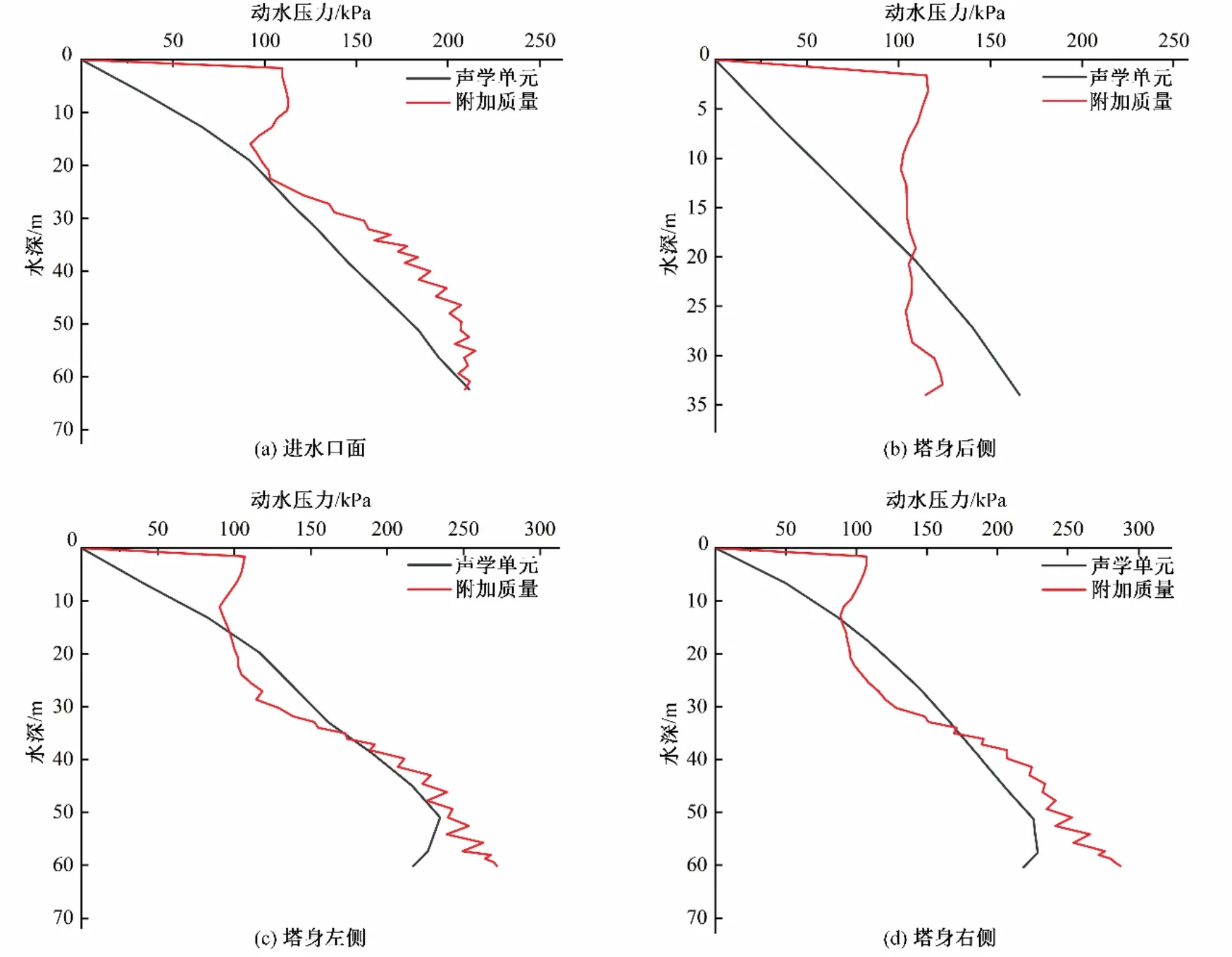
图5 声学介质与附加质量各迎水面动水压力对比图Fig.5 Comparison of hydrodynamic pressure of acoustic medium and added mass at each surface

综上所述，声学单元模型动水压力普遍小于附加质量模型，两者动水压力最大值接近。声学单元模型的动水压力曲线不受塔体加速度分布和塔体变形影响且动水压力曲线规律。

3.3 进水塔动力响应分析

3.3.1 位移与加速度分析

声学单元模型与附加质量模型的进水塔顶部特征点相对位移图和加速度时程曲线图如图6和图7。

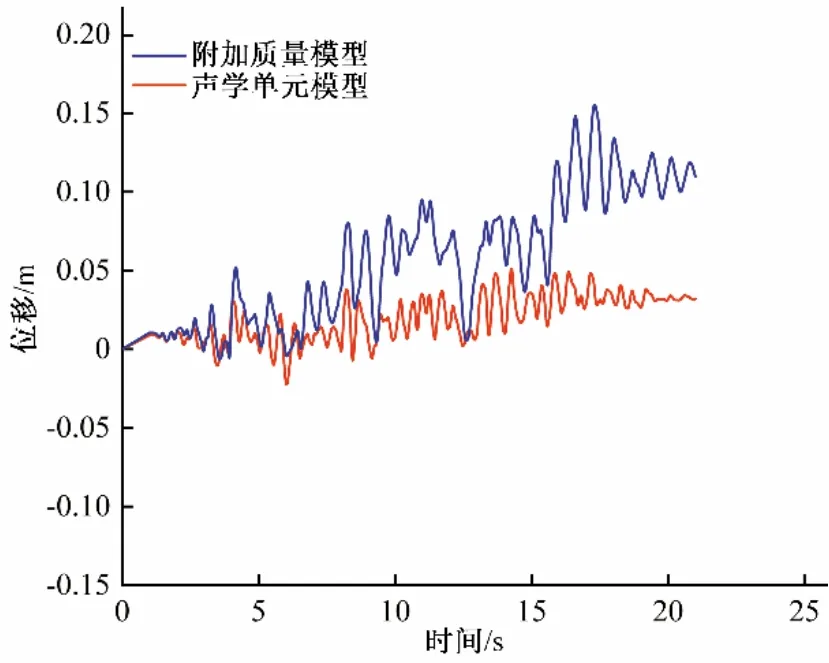
图6 不同工况下塔顶特征点相对位移时程曲线Fig.6 Relative displacement time history curves of characteristic points at the top of the tower under different working conditions

图7 不同工况下塔顶特征点加速度时程曲线Fig.7 Acceleration time history curves of characteristic points at the top of the tower under different working conditions

由图6 可知，其中声学单元模型的特征点位移普遍小于附加质量模型。声学单元模型作用下进水塔顶部最大位移出现在14.25 s，最大值为0.05 m；附加质量模型下进水塔顶部最大位移出现在17.34 s，最大值为0.15 m。声学单元模型相较于附加质量模型减小0.10 m，下降幅度为66.77%。

由图7 所知在进水塔顶部特征点加速度分析中，声学单元模型下的加速度略小于附加质量模型，声学单元模型下的特征点加速度最大值为4.37 m/s2；附加质量模型下特征点加速度最大值为4.89 m/s2。其中声学单元模型相较于附加质量模型加速度减小0.52，下降幅度为10.67%。

3.3.2 应力分析

从表2 和图8 可知两种模型的最大主应力值以及最不利的应力分布情况。前期两种模型应力分布都主要之中在塔身和混凝土回填处并向进水塔两侧延伸，这是由于进水塔的外部结构出现变化，导致容易产生应力集中现象。随着时间变化，声学单元模型中最大拉应力值为2.09 MPa，附加质量模型中最大拉应力值为2.61 MPa，声学单元模型较附加质量模型降低幅值约为19.92%；声学单元模型最大压应力为2.84 MPa，附加质量模型中的最大压应力值为3.60 MPa，声学单元模型较附加质量模型降低幅值约为21.11%。

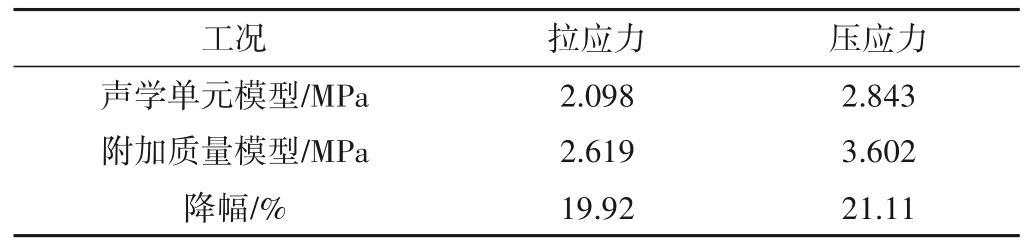
表2 不同工况下应力极值Tab.2 Stress extremes under different working conditions

图8 不同工况下最大主应力云图Fig.8 Cloud diagram of maximum principal stress under different working conditions

3.3.3 损伤分析

图9 和图10 分别为不同模型下进水塔的地震损伤云图。在地震作用2.56 s 时，声学单元模型下进水塔塔体后部与回填混凝土相互作用面处出现初步的损伤，于此同时在附加值量模型下塔体也出现损伤，损伤面积较大；两种模型都有向进水塔塔身两侧和塔身与底座连接处延伸的趋势。

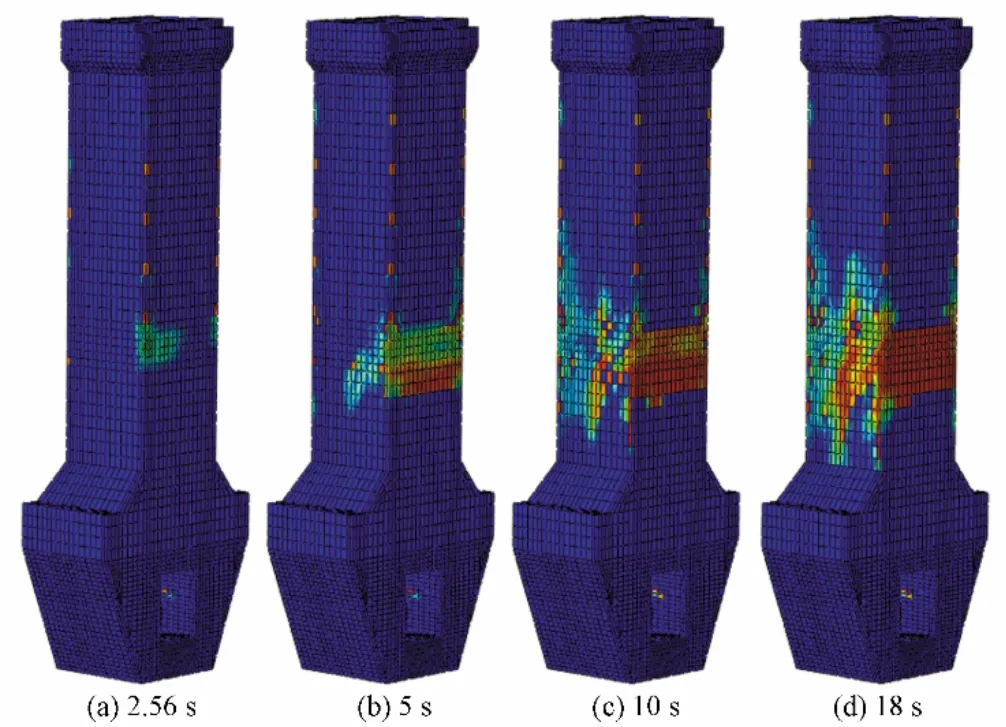
图9 不同时刻声学单元模型的进水塔损伤云图Fig.9 Damage cloud diagram of inlet tower of acoustic unit model at different times

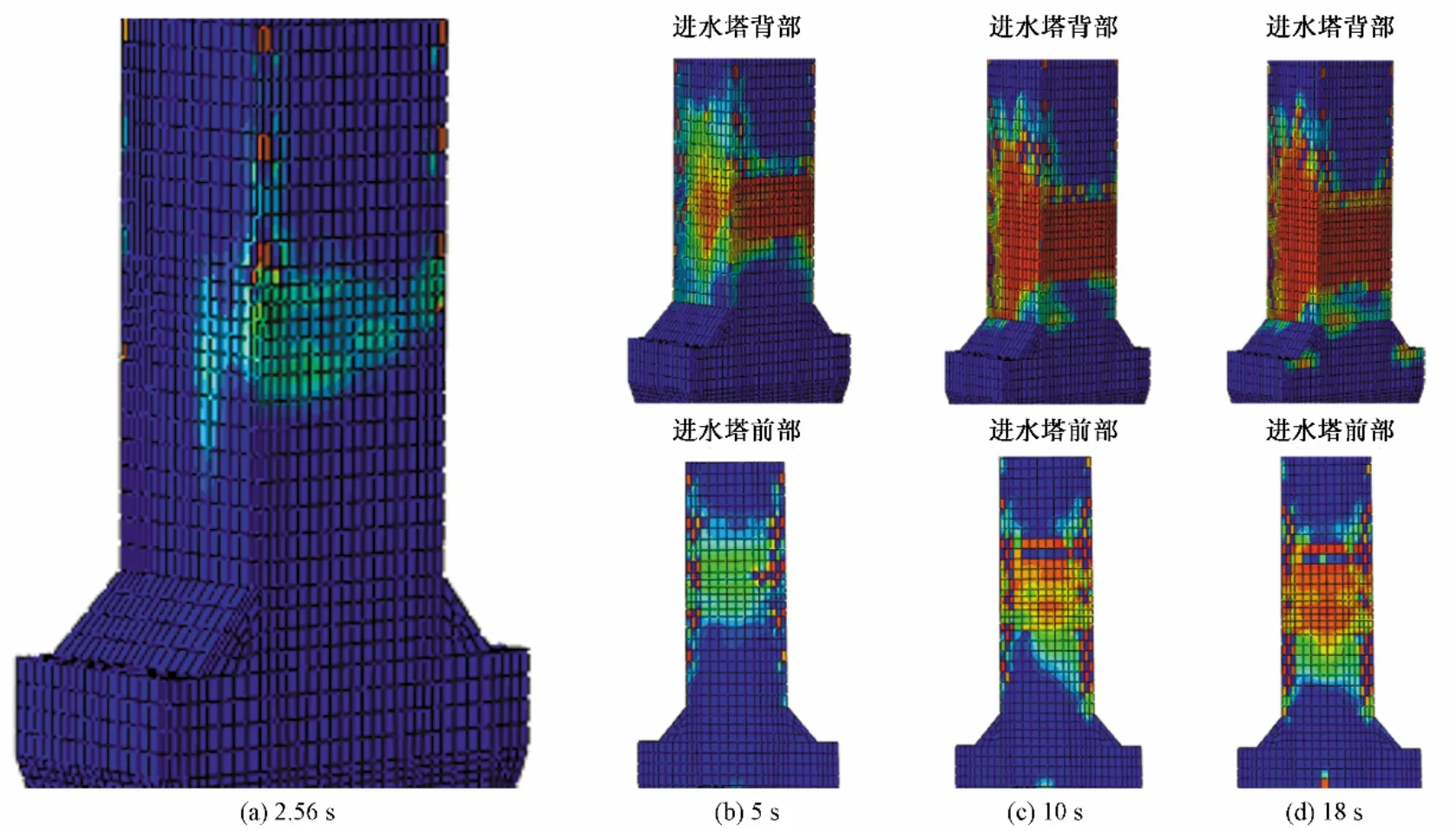
图10 不同时刻附加质量模型的进水塔损伤云图Fig.10 Damage cloud images of water intake tower with added mass model at different time points

在地震作用5 s时，两种模型下的进水塔塔体在开始出现的部位上损伤逐渐加大，损伤部位都逐渐向塔身下部扩散。声学模型作用下，损伤面积同时向上游面扩散，进水塔前部并未出现损伤；附加质量模型作用下，进水塔前部较声学单元已出现初步损伤，进水塔背部较声学单元损伤面积增大，且更加剧烈。

在地震作用10 s 时，声学单元模型作用下的损伤在塔体后部与回填混凝土相互作用面向塔体四周有小幅度的扩散，损伤面积通过塔身两侧向上游面进一步扩散，损伤程度进一步加剧；附加质量模型损伤情况继续向塔身与底座连接处方向扩散，进水塔前部损伤加剧。附加质量模型损伤面积最大，且更剧烈。

在地震作用18 s 时，两种模型的进水塔各部位损伤不再出现扩散和加剧，声学单元模型作用下，损伤面积没有继续向塔身和塔座连接处扩散，但是损伤程度进一步加剧。损伤面积继续通过塔身两侧向上游面扩散，但是损伤程度不剧烈；附加质量模型作用下，损伤面积达到二者模型最大，进水塔侧部和前部较声学单元模型出现较大损伤面，且形成损伤贯通区，损伤程度较声学单元模型剧烈。

通过以上分析可知，声学单元模型的进水塔损伤出现的位置主要在塔体后部与回填混凝土相互作用面；而附加质量模型不仅在塔体后部与回填混凝土相互作用面出现剧烈损伤，还在塔身与塔座交界面出现损伤。之所以在这两处位置出现损伤，是因为外部结构的改变使得进水塔在这些更加容易产生应力集中，从而出现损伤，和进水塔的材料强度不一致，从而刚度发生改变导致出现损伤。声学单元模型较附加质量模型在前期并没有在进水塔前部产生初步损伤，且在后期声学单元模型在进水塔前部损伤并不明显，在进水塔塔身左右两侧较附加质量模型并没有产生较大范围损伤。声学单元模型出现的损伤范围和损伤的剧烈程度都小于附加质量模型。

基于声学单元理论的进水塔-库水模型的损伤发展趋势与蒋才［22］等人的进水塔动力模型破坏试验结果（图11）基本一致，其中破坏实验采用三向六自由度模拟地震水下振动台进行，破坏实验进水塔原型同为中国西南地区泄洪洞进水塔，试验峰值加速度为0.3g，这与本文三维有限元模型及地震荷载数据基本一致，二者具有一定工程相关性。由于模拟时考虑了回填混凝土对塔体的作用，声学单元模型在震动后期会出现裂缝扩散，从而说明该方法在实际工程设计中具有一定的精确性和适用性。

图11 进水塔动力模型破坏试验结果Fig.11 Failure test results of dynamic model of water intake tower

4 结 论

本文以羊曲水电站为例，基于声学介质理论模拟可压缩动水压力，通过ABAQUS 建立进水塔-库水-地基三维模型，研究在声学单元模拟下的进水塔自振特性，进水塔动力响应以及损伤特性的影响，可得出以下结论。

（1）进水塔模态分析时，声学单元模型的各阶频率较附加质量模型普遍较高。根本原因是附加质量模型模拟动水作用改变节点质量所导致，而声学单元模型的施加方法更加符合真实水体存在的方式。

（2）进水塔动水压力计算时，声学单元模型动水压力值较附加质量法略小。外包络线不同于附加质量模型，不受塔身变形和加速度分布不均匀影响，从而呈现抛物线的分布规律，各迎水面的动水压力分布规律相似，随水深增大而增大。

（3）进水塔的动力响应分析时，在声学单元模型模拟动水压力作用下，进水塔塔顶部位移、加速度、拉应力、压应力都较附加质量模型有所减小，减小幅度分别为66.77%、10.67%、19.92%、21.11%。

（4）进水塔损伤分析时，在声学单元模型作用下，损伤扩散速度、损伤面积、损伤程度都较附加质量模型小，且声学单元模型与物理模型试验结果相一致，从而说明声学单元模型在实际工程设计中具有一定的精确性和适用性。