集群航天器鲁棒自适应快速任务分配

张润德，蔡伟伟，杨乐平，范大伟

(国防科技大学空天科学学院，长沙 410073)

0 引 言

随着网络技术的飞速发展和空间任务的日趋复杂,航天领域发展逐渐呈现出从单一、大型航天器到分布式空间系统的新趋势[1-2]。集群航天器以其灵活性、鲁棒性、自适应性等优点受到学者们的广泛关注[3]。集群航天器任务分配可表示为多约束条件下的离散空间组合优化问题,其目的在于建立航天器和任务之间的映射关系,以保证每个航天器在对应的时间窗口内执行特定的活动[4]。受通信能力、任务需求、机载存储能力、计算能力和轨道特性等诸多因素限制,集群航天器快速任务分配仍是一项极具挑战的工作。

根据控制框架的不同,集群航天器任务分配方法可分为集中式和分布式两大类。集中式任务分配主要包括最优化方法和启发式算法,其中以群智能算法、遗传算法、模拟退火等为代表的智能算法应用最为广泛[5]。分布式结构类似于自然界中生物种群,各航天器间通过信息交互协同完成各项任务。典型的分布式任务分配模型包括多智能体理论、分布式约束和类市场机制等[6]。类市场机制通过航天器间通信协商解决分配冲突,主要包括合同网法[7]和拍卖算法[8],其区别在于拍卖算法中每个航天器都是系统中的投标人,而合同网中接到任务的航天器会充当局部拍卖商的角色,主持竞拍程序[9]。Bertsekas[10]借鉴拍卖过程中根据参与者竞价决定商品归属的思路,率先提出了拍卖算法,并将其拓展至最短路径问题和任务分配问题。Zavlanos等[11]考虑去掉共享存储中心,在缺乏全局信息的情况下提出了完全分布式拍卖算法。但在智能体数大于任务数的场景中,同一任务可能被分配给多个智能体,导致任务分配失败。

燃料消耗是集群任务分配中一项关键指标,可通过相对运动轨迹规划进行数值求解,主要思路包括“优化+离散”的间接法和“离散+优化”的直接法[12]。间接法先基于变分法推导最优控制的一阶必要条件,再求解哈密顿边值问题获得最优控制序列,但非线性动力学模型和集群重构中各种复杂约束限制了间接法的应用范围。直接法通过离散状态或控制空间,将最优控制问题转化为非线性规划问题,利用数值优化算法进行求解,主要包括伪谱法[13]、凸优化[14-15]等算法,其中文献[16]表明序列凸优化的计算效率高于伪谱法,展现出其在在线规划中巨大潜力。但在集群航天器协同观测任务中,航天器终端边界条件不固定,即使是计算效率较高的凸优化算法也将消耗巨大的计算资源。针对航天器进入自然绕飞轨道问题,文献[17]基于凸松弛和线性投影技术提出一种混合凸优化算法,但该算法单次求解耗时约15～20 s,难以满足集群航天器自主快速任务分配的需求。

为提高燃料指标求解效率,Edelbaum[18]基于轨道根数推导了绝对坐标系下近圆轨道间连续推力转移所需特征速度的解析解,众多学者在此基础上考虑J2项摄动、共面小偏心率轨道转移和转移圈数等因素提出了一系列改进方法[19-21]。Edelbaum法适用于大范围连续推力转移轨迹的燃料预测,且通常基于多圈转移假设[22],难以直接应用于小范围、固定转移时间的相对运动轨迹规划问题。随着人工智能技术的飞速发展,越来越多的学者尝试利用机器学习和神经网络等技术解决航天领域的难题,在动力学建模、最优控制和任务设计等领域取得良好的应用[23-24]。朱阅訸等[25]分别利用分类和回归多层感知机预测转移轨迹的可行性和最优燃料消耗。Viavattene等[26]针对近地小行星交会任务,利用人工神经网络快速预测星际小推力转移的时间和燃料消耗,将神经网络的输出用于树搜索算法以确定可行的小行星交会序列,仿真结果表明计算效率可提升两个数量级。Li等[22,27]针对行星际多目标任务规划问题,利用深度神经网络预测小推力转移轨迹的最优转移时间和燃料消耗,仿真表明预测值的平均相对误差小于0.5%。现有文献中利用深度神经网络预测转移轨迹时间和燃料消耗指标研究多集中于大范围、小推力的行星间转移,对航天器相对运动轨迹预测研究较少。

针对航天器集群协同观测任务分配问题,本文提出一种基于深度神经网络和鲁棒自适应拍卖算法的快速任务分配策略。为快速求解航天器到达各观测点所消耗的燃料,本文利用深度神经网络直接预测转移轨迹的燃料消耗,以替代计算耗时的相对运动轨迹规划环节。为拓展拍卖算法的应用范围,通过构造虚拟收益矩阵和虚拟分配向量使其适用于航天器数与任务数不一致的分配问题。根据航天器集与任务集的不匹配度自适应调整报价增量,以提高算法的收敛速度。此外,考虑到分配过程中通信失联、航天器故障等不确定因素,通过在线调整故障卫星的收益和报价矩阵,使得拍卖算法能快速进行任务重分配,从而提升算法鲁棒性。

首先,在相对运动框架下描述集群航天器协同观测任务,对观测收益、燃料消耗和任务分配问题进行数学建模。其次,设计深度神经网络预测转移轨迹的燃料消耗,利用凸优化算法生成训练数据,针对不同结构的神经网络进行训练和优化,并对比其性能。再次,提出一种改进的鲁棒自适应拍卖算法,以提高任务分配的计算效率和精度。最后,通过数值仿真验证鲁棒自适应拍卖算法的性能。

1 问题描述

航天器相对运动通常在如图1所示的Hill坐标系中表示,坐标系原点位于目标航天器质心处,x轴与目标航天器地心矢径rt方向一致,y轴在轨道面内与x轴垂直,并指向运动方向,z轴由右手法则确定。

图1 Hill坐标系示意图Fig.1 Diagram of Hill coordinate

当观测航天器初始相对状态中长期项为零时,观测航天器可围绕目标航天器进行闭环周期性绕飞,且不需额外消耗燃料。绕飞轨迹在轨道面内投影为2∶1的椭圆,航天器的相对运动状态x(t)可由一组绕飞轨道参数[b,c,yc,φ,ψ]进行表示[28]。

(1)

式中:n为目标航天器的平均轨道角速度;b为绕飞轨迹在轨道面内投影椭圆的半短轴;c为绕飞轨迹在z轴方向的最大值;yc为绕飞中心在y轴方向的偏移量;φ和ψ分别为轨道面内和面外相位角。

相较于远距离观测和地面观测,航天器抵近观测可获得更加精细的目标特征数据。利用多航天器协同观测可有效提升任务时效性,尤其是针对高轨航天器。单个航天器对地球同步轨道目标绕飞观测一周耗时约24小时,观测效率较低。利用多航天器协同观测,再将多个航天器的观测信息融合,可有效缩短所需观测时间。

集群航天器协同观测任务如图2所示。初始时刻,集群航天器在己方航天器周围进行伴飞。任务开始后,需从伴飞集群中选择部分或全部航天器进入目标航天器的绕飞轨道,对目标执行协同观测任务。首先,需要优化观测点的相对状态。受光照条件影响,每个观测点对应的观测收益不同,集群中各航天器转移至不同观测点所需消耗的燃料也不相同。其次,综合考虑观测收益和燃料消耗,确定集群中各航天器前往各观测点的实际收益。最后,求解任务分配序列为集群内各航天器分配任务,使得集群整体收益最大。

图2 协同观测任务示意图Fig.2 Diagram of cooperative observation mission

由式(1)可知,φ决定航天器在绕飞轨迹上的相对位置。假设集群航天器在绕飞轨道等相位分布,定义首个观测点的面内相位角为φ1,则第j个航天器的面内相位角为

(2)

式中:0≤φ1<2π/Nt,Nt为观测点个数,可根据观测航天器数量、绕飞轨道周期、任务时间和观测角度等参数提前设定。因此,当绕飞轨迹构型确定后,给定相位角φ1,即可确定所有观测点的相对状态。

集群航天器执行协同观测任务时,需同时考虑观测收益和转移轨迹的燃料消耗。当航天器相机视场内出现强烈光源时,电荷耦合器件会发生浮散现象,导致成像不清晰。因此,观测航天器进行成像观测时,需满足光照角约束。

(3)

式中:rct和rcs分别表示地球惯性坐标系下观测航天器指向目标航天器和太阳的矢量。若θ小于预设的θmin,表示此时成像质量无法满足要求。此外,当目标航天器进入地球阴影区时,观测航天器也无法对其成像。因此,航天器i在观测点j的观测收益可表示为

(4)

式中:tobs表示观测时长。当θ(t)≥θmin且目标航天器不处于地球阴影区时,oij(t)=1。否则,oij(t)=0。

航天器i机动至观测点j消耗的燃料最优轨迹优化问题可表示如下:

(5)

式中:i,k=1,2,…,Ns且i≠k,j=1,2,…,Nt。xi(t)和ui(t)分别表示集群中第i个航天器的相对状态和控制量,Ns为集群中航天器个数,xj表示第j个观测点的相对状态。动力学模型采用经典的Clohessy-Wiltshire方程,矩阵A和B的具体表达式参见文献[29]。Tmax为推进器最大推力值。xi(t0)=xi0和xi(tf)=xj表示航天器i的初始状态和终端状态分别为xi0和xj,C=[I3×303×3],Rcol为两航天器间最小容许距离。

任务指派的决策变量c∈Ns×Nt,cij∈{0,1},其中cij=1表示第i个航天器部署在第j个观测点。否则,cij=0。为使得每个观测点只有一个航天器,且每个航天器至多只前往一个观测点,任务分配模型可表示如下:

(6)

式中:J=ω1O-ω2F。Jij表示航天器i执行任务j的实际收益等于观测收益减去燃料消耗,ω1和ω2为对应的收益系数。

综上所述,集群航天器协同观测任务分配主要包括优化相位角φ1、计算收益矩阵和任务指派三部分。如图3所示,相位角φ1决定所有观测点的相对状态,为相对运动轨迹规划提供终端边界条件。收益矩阵J为任务指派提供分配指标,任务指派确定的决策向量c最终决定集群航天器的总收益。

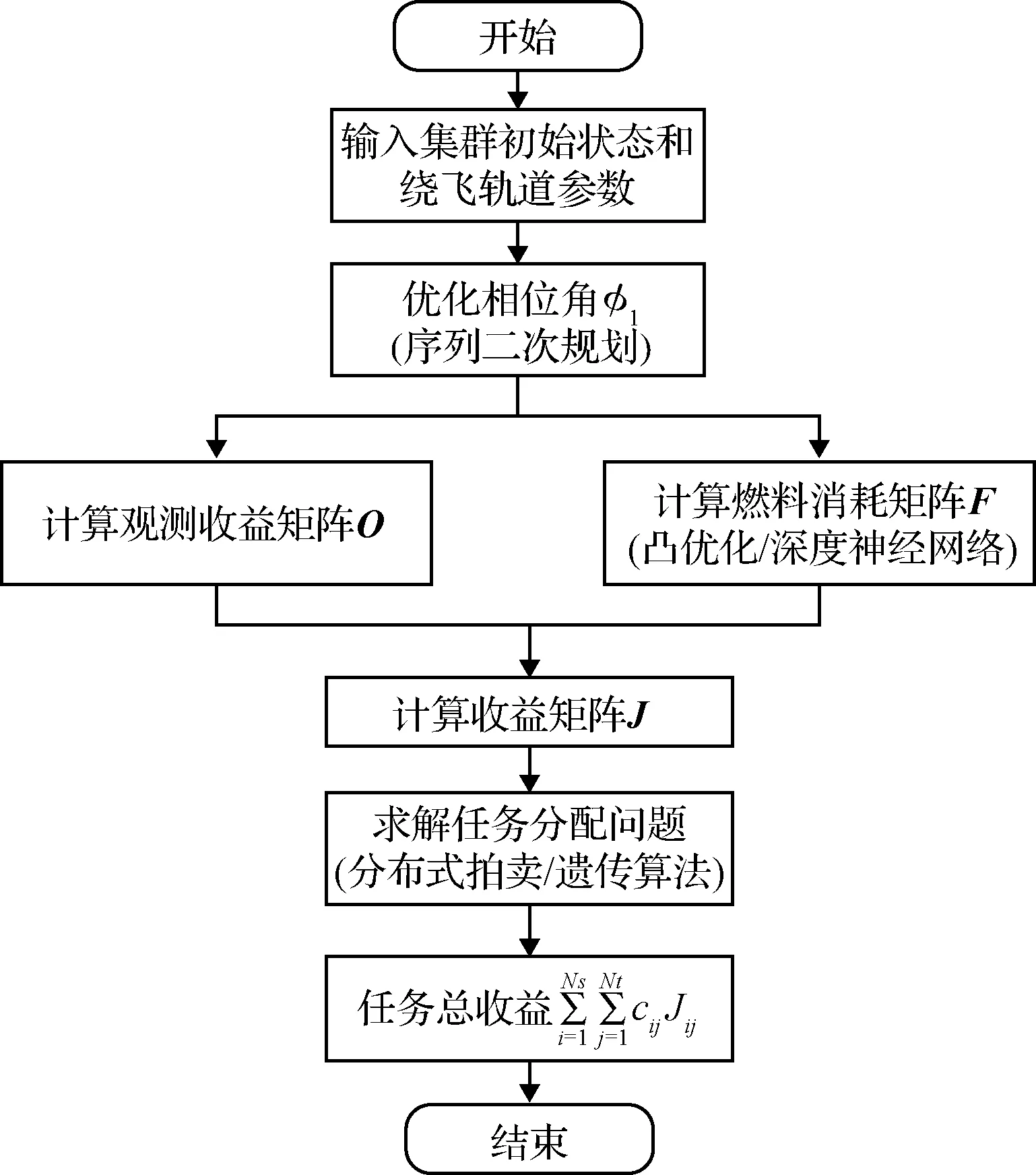
图3 集群航天器任务分配流程图Fig.3 Flow chart of task assignment for spacecraft swarm

2 基于深度神经网络的燃料消耗预测

航天器相对运动燃料最优轨迹规划问题可转化为非线性最优控制问题,并利用凸优化等数值优化算法进行求解。但随着集群规模增大,任务分配的计算量急剧增加,以至于现有计算条件难以满足在线规划的需求。为提高计算效率,本文利用深度神经网络直接预测航天器相对运动的燃料消耗,从而替代数值优化过程。

深度神经网络包含一个输入层、一个输出层和多个隐藏层,输入层和输出层的维度分别与输入和输入数据维度一致,每个隐藏层包含多个神经元。本文选用初始和终端绕飞轨道特征参数[b0,c0,φ0,ψ0,bf,cf,φf,ψf]作为神经网络的输入,最优控制对应的燃料消耗矩阵F为输出,如图4所示。

图4 深度神经网络示意图Fig.4 The diagram of deep neural network

2.1 数据生成与预处理

实际任务中航天器的尺寸远小于集群构形尺寸,卫星间发生碰撞的概率通常较小。为提高迭代效率,在任务分配阶段可先不考虑避碰约束,然后再评估最优分配方案是否会发生碰撞,若发生碰撞可利用文献[15]中基于序列凸优化和模型预测控制的闭环制导策略进行在线调整。因此,在离散化和解耦的基础上可将集群重构轨迹规划问题转化为如下凸优化问题:

(7)

式中:i=1,2,…,Ns,j=1,2,…,Nt,k=0,1,…,Nd-1,Nd为离散步数。xi(k)和ui(k)分别表示行航天器i第k步的相对状态和相对控制向量,Ad和Bd可由离散形式的相对运动方程推导而得。

假设目标航天器位于地球同步轨道,集群航天器从10 km外的伴飞轨道转移至相对坐标原点的绕飞轨道,集群航天器最大推力加速度为0.98 m/s2,飞行时长为800 s,绕飞轨道的各参数服从均匀分布,取值范围如表1所示。

表1 绕飞轨道参数取值范围Table 1 Value ranges of fly-by orbit parameters

在各参数的取值范围内随机生成绕飞轨道参数,构造相对运动初始和终端边界条件,再利用凸优化算法求解上述凸优化问题,得到对应的燃料消耗指标F。仿真共生成15万组数据,并按照8∶1∶1的比例构建训练集、验证集和测试集。

由于各参数间的数量级相差较大,采用最大-最小归一化方法对绕飞轨道参数和燃料消耗指标进行归一化处理。最大-最小归一化方法是深度学习数据预处理中常用的一种方法,可将样本转化为[0,1]区间内无量纲的纯数值,便于不同单位或量级的参数能够进行比较和加权,进而提升神经网络的收敛速度和精度,其定义如下:

(8)

式中:p为原始数据,pmax和pmin分别表示原始数据的最大值和最小值,p′为归一化之后的数据。

2.2 神经网络训练与优化

选用全连接神经网络,隐藏层的之间的激活函数为Relu函数。神经网络优化目标为训练样本与预测值之间的均方差。

(9)

神经网络规模主要取决于隐藏层的层数和神经元数目。网络规模过大会导致结构复杂、训练时间增长,甚至出现过拟合现象。网络规模过小难以拟合输入和输出之间的映射关系,无法满足训练精度。本文对比了不同结构的神经网络对训练结果的影响,神经网络的测试结果如表2所示。

表2 不同网络的相对误差对比Table 2 Comparison of relative errors of different networks

神经网络“3×20”表示该网络隐藏层数和隐藏层神经元数分别为3和20。由表2可知,神经网络的预测误差服从正态分布,且误差的均值接近零。第1-4组仿真中隐藏层的神经元数不变,随着隐藏层层数增加,相对误差的标准差先减小而后基本保持不变,其中7层和9层网络预测精度相近。对比第5-8组仿真中的7层神经网络,随着隐藏层神经元数增加,相对误差标准差先逐渐减小而后增大。对比第9-12组仿真,预测结果的相对误差标准差同样呈现先减小后增大的规律。表2中神经网络“7×140”和“9×120”的预测精度相近,网络训练时间分别为1.8和2小时。综合考虑训练精度和训练效率,本文选用神经网络“7×140”用于后续仿真中预测转移轨迹的燃料消耗,该网络预测相对误差的3σ区间为[-3.78%, 3.68%],即相对误差位于该区间的概率为99.73%。实际任务中可利用地面控制站的计算资源生成样本并训练神经网络,仅将训练后的神经网络参数上传至观测航天器上,避免占用宝贵的在轨计算资源。

为验证深度神经网络的适应性,利用上述针对地球同步轨道航天器设计的神经网络“7×140”分别预测低轨、中轨和高轨航天器相对运动的燃料消耗,其中每个轨道随机生成100个任务场景,神经网络“7×140”预测值相较于凸优化精确解的相对误差的均值和标准差如表3所示。仿真结果表明,在地球同步轨道上下100 km处,神经网络“7×140”的预测精度与该网络对地球同步轨道目标的预测精度相近。但当轨道高度与地球同步轨道相距较大时,其预测误差较大,可信度较低,需利用对应的轨道仿真数据重新训练神经网络。

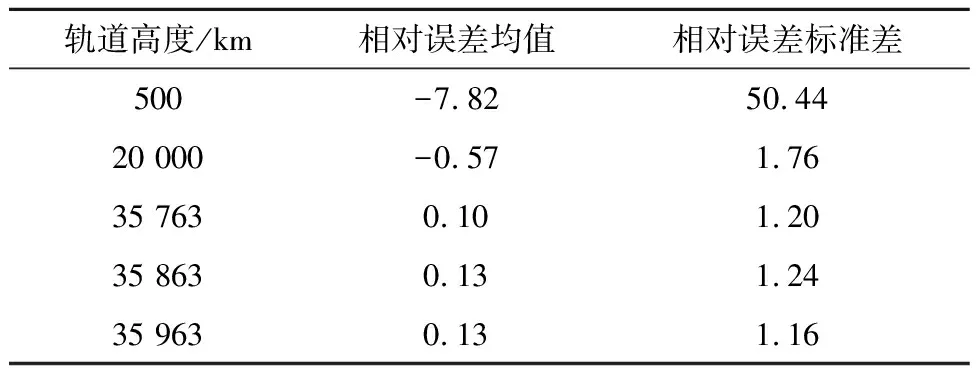
表3 不同轨道处燃料消耗预测相对误差Table 3 Relative errors of predicted fuel consumption at different orbits

3 鲁棒自适应拍卖算法

拍卖算法借鉴了人类社会中的竞拍流程,各航天器根据当前状态计算任务收益,通过与邻居通信了解对方的竞价信息并调整自身的任务报价,最终选择净收益最大的任务。

由于分配问题中任务数与航天器数可能不相等,本文通过构造虚拟收益矩阵和虚拟分配方案,将原问题转化为任务数与航天器数一致的分配问题,以便于应用分布式拍卖的算法。对航天器i执行如下步骤:

1)集群内每个航天器根据当前状态和观测点状态,分布式计算观测收益、燃料消耗,并构造收益矩阵J∈Ns×Nt,其中Jij表示航天器i执行任务j的收益。若Ns≠Nt,则通过补零的策略将J展为虚拟收益方阵Ns×Ns。

3)航天器i通过星间通信获取上一轮中所有邻居Ni(k)对任务j的最高报价p(k+1)及对应的最高出价者b(k+1)。

4)如果航天器i对目标任务的上轮报价小于等于此轮报价,且目标任务的最高出价者不是航天器i,则将净收益最高的任务分配给航天器i,同时在上轮报价的基础上增加γi,其中γi表示航天器i执行所有任务的最大净收益和第二净收益之差再加上增量ε。

(10)

3.1 ε自适应调整策略

增量ε会影响拍卖算法计算效率和精度,通过定义任务集和航天器集之间的不匹配度,可使得ε在迭代过程中可根据不匹配度自适应调整。

初始时刻航天器对所有任务报价均为零,所有航天器都倾向于执行收益最大的任务,而其他任务没有航天器执行,此时任务集与航天器集的匹配度较低。在迭代过程中,航天器不断提升自身报价,并根据净收益调整分配目标,最终实现任务与航天器一一匹配。定义如下指标M表征航天器集与任务集之间的不匹配程度

(11)

式中:

(12)

由式(11)和(12)可知,M∈[0,Nt]。若执行所有任务的航天器数量均不等于1,即M=Nt,ε可取较大值以快速提高任务报价,增加航天器集与任务集间的匹配程度。随着不匹配度M值的减小,ε值可逐渐减小,使得算法收敛精度更高。因此,为实现增量ε随不匹配度M自适应调整,定义如下线性变化关系

(13)

式中:εmin和εmax为设定的最小和最大增量。

3.2 鲁棒自适应拍卖算法

在实际任务中,考虑到航天器发生故障失去任务能力、通信失联等不确定因素,需要针对不确定情况下任务分配展开研究。集中式分配方法根据已知全局信息为集群中所有航天器分配任务,若发生不确定事件,则需在初次分配结束后根据更新的状态信息重新分配。分布式分配方法在优化过程中每个航天器需要反复获取其他航天器的报价信息以调整自身报价,若某个航天器发生故障或通信失联,可以直接调整其收益和报价信息进行鲁棒规划。

定义通信矩阵G∈Ns×Nt,若在第k迭代中航天器i能接收到航天器j的报价信息,则Gij(k)=1。若航天器i无法接收到航天器j的报价信息,或收到航天器j的故障信息,则Gij(k)=0。假设航天器间采用双向通信,则Gij(k)=Gji(k)。

假设集群中所有航天器i在第k轮迭代中都无法接收到航天器j的报价信息,或仅收到航天器j发出的故障信息,则认为航天器j失效,无法继续执行任务,其中i,j=1,2,…,Ns且i≠j。由于航天器j已失去任务能力,令其执行所有任务的收益均为零,即

(14)

在前k-1轮迭代中,其他航天器已经分配到相应的任务,为避免失效航天器j对其他航天器任务分配结果的干扰,将其第k-1轮报价置零,即

pj(k-1)=0

(15)

通过将失效航天器的收益和报价信息置零,可降低失效航天器的后续分配过程中的竞争力。若任务数小于航天器数,则失效航天器将无法分配到实际任务。若任务数等于航天器数,则失效航天器只能分配到收益较低的任务,从而使得整个集群收益最大。完整的鲁棒自适应拍卖算法流程如图5所示。

图5 鲁棒自适应拍卖算法流程图Fig.5 Flow chart of robust adaptive auction algorithm

4 仿真校验

为验证鲁棒自适应拍卖算法性能,在给定观测点的场景下,针对不同规模的分配问题和不同ε值进行数值仿真。此外,针对集群航天器协同观测任务分配问题展开仿真,并与凸优化和遗传算法进行对比。

4.1 鲁棒自适应拍卖算法性能验证

假设仿真开始时间为2022年6月16日0时0分0秒,目标航天器在地球惯性坐标系下的初始位置和速度分别为rt=[37 097.59, 20 029.27,46.28]Tkm和vt=[-1.46, 2.70, 0.11]Tkm/s。初始绕飞轨道参数为b0=1 000 m,c0=900 m,yc0=10 km,ψ0=-π/6,首星面内相位角为π/10,其他卫星呈等相位分布。目标绕飞轨道参数为bf=1 000 m,cf=800 m,ycf=0 m,ψf=π/4。绕飞时长为24小时,观测收益系数ω1=1/864,燃料消耗系数ω2=1。集群航天器最大推力加速度为0.98 m/s2,转移时间为800 s。由于集群航天器间相对距离较近,假设所有航天器均能双向通信。在分布式迭代中过程,通信拓扑中邻居信息、收益矩阵、价格矩阵、报价增量和当前分配矩阵是每个航天器算法模块的输入,航天器根据输入信息调整任务报价,获得收益最高的任务,并将报价信息传递至通信拓扑中,进入下一轮迭代,直至算法收敛[9]。仿真计算机处理器主频和内存分别为3.0 GHz和16 GB。为排除非线性优化算法和燃料预测方法的影响,令首个观测点面内相位角为0,其他观测点在绕飞轨道上等相位排列,利用深度神经网络预测转移轨迹的燃料消耗。

首先,在航天器与观测点数目相等的任务场景中验证拍卖算法、遗传算法和蚁群算法的计算性能,参数设置如表4所示,其中优化终止条件取值20表示收益值连续20代不变则认为算法收敛。仿真中遗传算法的优化终止条件设为20、50和100,分别用GA20、GA50和GA100表示。

由图6(a)可知,拍卖算法和遗传算法的计算耗时均小于1 s,优于蚁群算法。图6(b)表示遗传算法和蚁群算法相较于拍卖算法的总收益差值,遗传算法和蚁群算法的总收益值均低于拍卖算法,且总收益差值随问题规模增加而整体呈现放大趋势。此外,随着优化终止条件取值增大,遗传算法的计算精度逐渐提高,计算效率逐渐降低。在当前仿真条件下,拍卖算法的计算效率和精度均优于遗传算法和蚁群算法。由于GA100的计算精度最接近拍卖算法,后续仿真中遗传算法的优化终止条件设为100代。此外,由于种群初始化和进化操作是基于概率随机确定的,所以遗传算法和蚁群算法每次的计算结果略有不同。对于鲁棒自适应拍卖算法而言,当ε取值范围固定,每次计算结果一致。

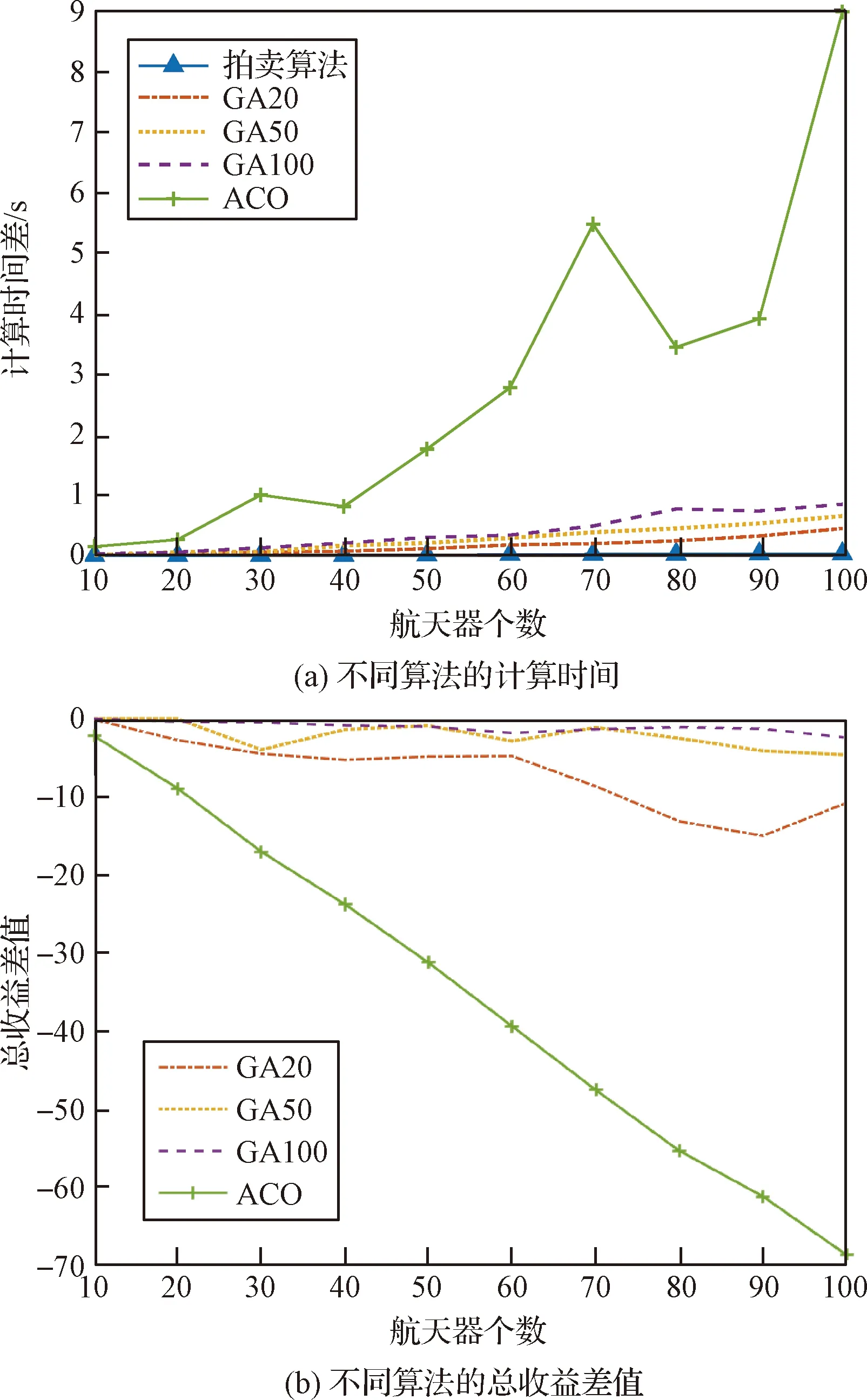
图6 不同算法的性能对比Fig.6 Performance comparison of different algorithms

其次,为验证ε自适应调整策略的性能,在不同规模的任务场景中展开仿真,在各个场景中观测点数与航天器数目一致。传统拍卖算法的ε值分别取0.01、0.05、0.1,鲁棒自适应拍卖的εmin=0.01,εmax=0.1,仿真结果如图7所示。为便于对比,图7(b)中纵轴代表拍卖算法的总收益值与遗传算法的差值,遗传算法的参数设置与表4中GA100一致。

图7 拍卖算法取不同ε值的性能对比Fig.7 Performance comparison for auction algorithm with different ε

由图7(a)和可知,随着分配问题规模变大,拍卖算法和遗传算法所需的计算时间都逐渐增加。基于ε自适应调整策略的鲁棒自适应拍卖算法所需计算时间约为ε=0.01对应的拍卖算法一半。随着ε的减小,拍卖算法的总收益逐渐增加。鲁棒自适应拍卖的总收益与ε=0.01时的拍卖算法的总收益极为接近。综上所述,ε∈[0.01, 0.1]的鲁棒自适应拍卖计算精度与传统拍卖算法ε=0.01相近,但计算耗时仅为其一半。

最后,针对集群任务分配过程可能存在航天器故障、通信失联等不确定情况展开仿真。假设航天器个数和任务数均为100个,在拍卖算法的迭代过程中,随机确定发生故障的航天器的编号和迭代轮数,采用任务重规划和鲁棒自适应拍卖进行任务再分配。任务重规划的思路是在发生故障后,根据更新的航天器信息重新采用分布式拍卖算法进行任务分配。鲁棒自适应拍卖则是在原有的报价信息基础上,将故障航天器的收益和报价信息置零,继续规划,仿真结果如表5所示。

表5 不确定条件下拍卖算法的分配结果Table 5 Task assignment results of auction algorithm under uncertainty

表5中第一行数据表示第34号航天器在第511轮迭代中出现故障,集群中其他卫星根据更新的信息重新分配任务需迭代11 964轮,则总迭代次数为12 475。若采用鲁棒自适应拍卖算法则只需迭代11 941次,两种分配方法的收益误差为0.009。由表5可知,不确定情况下两种任务重分配方法都能成功完成任务分配,且分配结果的任务总收益基本一致。由于鲁棒自适应拍卖能利用已有的分配信息,及时调整收益矩阵和报价信息,其总迭代次数在所有算例中均小于任务重分配策略。此外,若故障发生较早,则两种方法的迭代轮数相近,若故障发生较迟,则鲁棒自适应拍卖算法的迭代轮数远小于任务重分配策略。

4.2 在线任务分配方法验证

针对航天器集群协同观测任务分配问题,本节设计两组不同规模的算例以验证基于深度神经网络和鲁棒自适应拍卖算法的快速任务分配方法的性能。

首先,从包含6个航天器的集群中选择4个航天器执行协同观测任务。相位角φ1优化采用序列二次规划方法,航天器转移燃料消耗分别采用凸优化和深度神经网络进行计算,任务分配基于遗传算法和鲁棒自适应拍卖算法。由于非线性优化算法的计算结果受初值影响较大,仿真中每个算例重复计算10次,取收益最高的一组解作为最优解,并统计10次仿真的平均计算时间,仿真结果如表6所示。

表6 不同方法的任务分配结果Table 6 Task assignment results of different methods

表6中CVX和DNN分别表示利用凸优化和深度神经网络求解转移轨迹的最优燃料消耗。φ1表示目标绕飞轨道上首个观测点的面内相位角,指派方案中[0,1,2,3,4,0]代表航天器1和6不机动,航天器2至5分别转移到观测点1至观测点4。

基于凸优化和深度神经网络的方案总收益分别为274.31和273.51,相对误差小于0.3%。图8中展示了前两个算例中各航天器乘以收益系数后的观测受益、燃料消耗和实际收益。航天器1和6未执行任务,对应的收益值始终为零,航天器2至5的观测收益、燃料消耗和实际收益基本一致,再次证明基于深度神经网络的燃料预测方法的可靠性。

图8 集群中各航天器的收益值Fig.8 Performance for each spacecraft in swarm

对比表6中前两种方法的计算时间可知,基于凸优化的方案在优化连续变量φ1过程中需多次调用底层的凸优化算法求解转移轨迹,因此计算效率较低,CVX-GA方案耗时1 962.33 s,而DNN-GA方案直接利用深度神经网络预测燃料消耗,仅耗时1.47 s,计算效率提升约两个数量级。对比CVX-GA和CVX-DA方法的仿真结果可知,CVX-DA方案将凸优化求解最优转移轨迹的计算过程分散到集群内各个航天器上,其仿真耗时仅为CVX-GA方案的1/6。同理,对比DNN-GA和DNN-DA方法的计算结果可知,DNN-DA方案的计算效率明显优于DNN-GA方案。综上所述,基于深度神经网络和鲁棒自适应拍卖算法的在线分配方法能在保证计算精度的同时,将计算效率提升约两个数量级。

为进一步验证基于深度神经网络的分配方案在不同集群重构问题中的性能,假设集群航天器的规模和观测点数为10至100个。由于基于凸优化的CVX-GA和CVX-DA方案耗时过长(大于24小时),表7中仅展示DNN-GA和DNN-DA方案的仿真结果。

表7 不同规模集群任务分配结果Table 7 Task assignment results of swarm with different sizes

由表7可知,随着集群航天器规模增大,任务分配的平均计算时间也逐步增加。由于采用分布式框架,DNN-DA的计算效率比DNN-GA提高了约一个数量级,两者的总收益相近。值得强调的是,基于凸优化的CVX-GA和CVX-DA方法在当前计算配置下难以求解上述算例,而DNN-DA解决包含100个航天器的大规模集群的任务分配问题仅耗时8.72 s,为在线求解集群航天器任务分配问题提供新思路。

5 结 论

针对集群航天器协同观测任务分配问题,本文提出了一种基于深度神经网络和鲁棒自适应拍卖算法的快速任务分配策略。深度神经网络可用于预测航天器相对运动转移轨迹的最优燃料消耗,数值仿真表明神经网络预测的相对误差小于4%。鲁棒自适应拍卖算法适用于任务数与航天器数不一致的分配问题,且能有效应对通信失联、航天器故障等不确定情况。基于深度神经网络和鲁棒自适应拍卖算法的在线任务分配方法可在保持计算精度的同时,将计算效率提升约两个数量级。未来工作将进一步考虑通信代价对分布式任务分配算法的影响。