基于稀疏字典优选的织物疵点检测方法
王小虎, 潘如如, 高卫东, 周 建
(生态纺织教育部重点实验室(江南大学), 江苏 无锡 214122)
在生产过程中织物疵点是由原料、工艺、机械故障及人为因素等原因所导致的。纺织品表面含有疵点将严重降低产品的质量,导致织物价格下降。检测作为产品质量控制的重要环节,在生产过程中占有重要地位,其中疵点检测是关键的部分。目前疵点检测主要由人工来完成,但人工验布由于检出率低、速度慢、人员成本高等缺陷,无法达到高效率、高质量智能化生产要求,因此,将快速而可靠的图像处理技术应用在疵点检测中,实现织物疵点自动化检测具有重要意义,也是近年来的研究热点。
根据不同的织物图像处理方法,织物疵点检测可分为5类[1]:基于结构的方法、基于统计的方法、基于频谱的方法、基于模型的方法以及基于学习的方法。结构法通过从织物中提取图像的基础纹理结构获得结构特征,疵点的存在破坏了原有的结构纹理,通过与正常纹理比较相似度可检测出疵点[2]。基于统计的方法主要利用像素及其邻域的灰度属性,分析纹理区域的灰度一阶、灰度二阶或灰度高阶属性。常用的统计方法有直方图统计法[3-4]、灰度共生矩阵[5-7]、数学形态学[8]等。基于频谱的方法是利用织物纹理的周期性与频谱特性的相似,将分析频谱的方法应用于图像纹理,傅里叶变换[9]、Gabor变换[10]、小波变换[11]等是其中常用的方法。基于模型的方法是通过假设纹理服从特定分布模型和该模型的参数,从而根据此特定分布模型来判断被测图像,实现疵点检测,适用织物表面特征变化没有规律的情况。常见的有自回归模型和马尔科夫随机场。基于学习的方法主要有字典学习[12-13]、深度学习[14]、支持向量机等。
稀疏表达理论是近年来研究热点问题之一,因其优秀的数据特征表达能力被广泛应用于人脸识别[15]、图像去噪[16]等领域。稀疏表示理论中最为重要的角色就是稀疏字典。通过学习所得的稀疏字典能够更好地适应信号特征,允许字典通过学习对输入信号进行更有效的表达。
对于疵点检测来说,稀疏字典能够对原织物纹理结构实现很好的表达和近似,因此应用稀疏字典方法进行织物疵点检测可取得满意的效果。但稀疏字典的学习与求解耗时较长,难以应对工业场景下实时检测要求。为此,本文采用字典分组策略对稀疏字典进行优化,在保证检测效果的同时提高算法速度。
1 稀疏表达理论
在信号处理领域中,信号通常可分解为一些基本元素或函数的线性组合来进行表达。对织物纹理信号线性表达的基本思路是寻找一些基元素(即字典),这些基元素的线性组合可在一定的约束下对原信号进行最优的近似(重构)。通过学习所得的稀疏字典能够更好地适应信号特征,允许字典学习对输入信号进行更有效的表达。对于织物疵点检测来说,这种表达方式能够更有效地还原织物特征或者结构,突出疵点部分,有利于后续的疵点区域识别。
稀疏表达通常使用过完备字典,即字典数量大于其特征维度,对特征表达是只用过完备字典中的少量元素,在l0条件下,假设字典大小为k,表示为D=[d1,d2,…,dk]∈Rm×k,字典D中的每一列dk∈Rn即为1个原子,样本数据矩阵为X,设α为编码稀疏矩阵,记为α=[α1,α2, …,αn]∈Rk×n,则X≈D×α, 如果αi中仅有α0(α0≪k)个非零个数,则αi的稀疏度为T。稀疏字典的求解可看作为一个以某种近似条件为目标函数的数学优化问题,通常将l0范数松弛为l1范数进行求解,在D已知下的稀疏编码问题如式(1)所示:
(1)
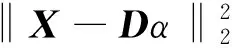

(2)
式中,C即验证此约束的矩阵凸集。此时结合以上2个式子可改写成D和α的联合优化问题,如式(3):
(3)
此时式(3)是非凸函数,无法求解,但当D或者α其中1个变量确定下来时,目标函数对另一个变量则成为凸优化问题,求解稀疏系数可以采用最小回归角(LARS)算法。
2 算法流程与字典优化
2.1 算法流程
如图1所示,在学习阶段,输入为正常织物样本图像,并划分为一定大小的子窗口,展开排成列向量后组合成1个矩阵。对样本集合矩阵进行稀疏字典学习,并且对得到的稀疏字典D进行优化选择并分为n组(优化策略详见下节),作为后续检测用字典库集合Ds={Di},i=0,1,2,…,n-1。
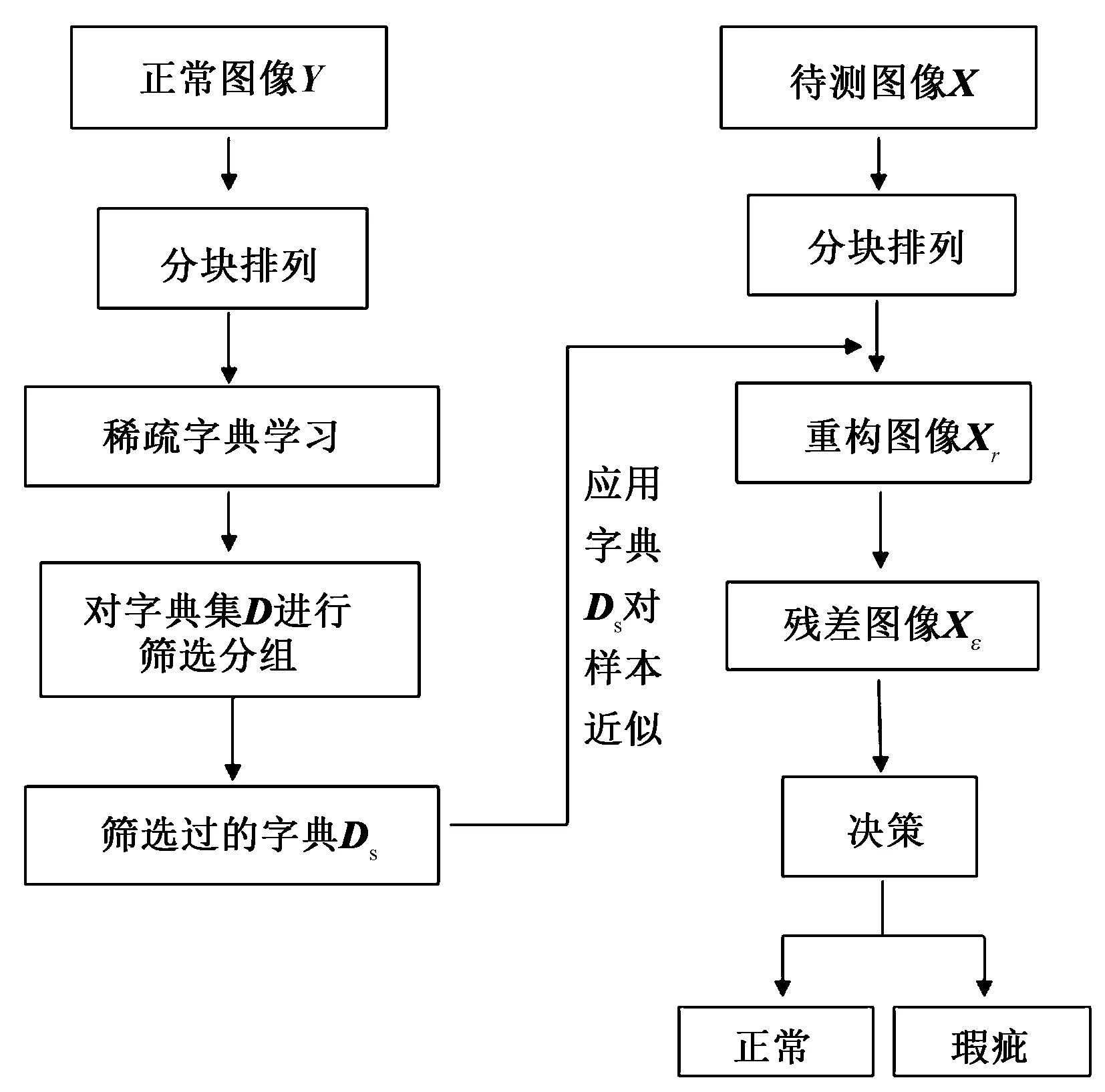
图1 算法流程图Fig. 1 Algorithm flow chart
在测试阶段,输入有疵点图像X,划分子窗口提取所有样本,排成列向量组合成矩阵Xt,利用字典库Ds中所有组合Di对矩阵用最小二乘法求解得到相应系数αi,由式(4)可得重构图像Xri,将其与排列组合过的图像矩阵Xt相减取绝对值的平方即可突出疵点部分如式(5):
Xri=D×αi
(4)
Xεi=|Xt-Xri|2
(5)
式中:Xri为重构图像;Xt为取块排列后的图像矩阵;Xεi为残差图像。
原图与残差图像如图2所示。
由于有n组字典,最终得到的残差图像也有n张,将所有残差图像合并得到Xε(图2为将子窗口还原后的残差图像),对于残差图像Xε需要对每个子窗口样本进行判断,并标记疵点样本,最后根据疵点样本数量判断是否为正常图像(允许一定程度误检)。

图2 原图与残差图像Fig. 2 Original image(a) and residual image(b)
2.2 字典优化
对于普通字典学习即无稀疏约束的字典学习而言,选择无疵点样本进行学习,此时织物图像的纹理信息等已经包含于学习所得字典中,但得到的字典对于待测图像进行线性表示时,所得的重构图像中易包含疵点部分,其残差图像不能很好地突出疵点区域,导致检测精度不高。
对于稀疏字典学习而言,字典通常为过完备字典,字典个数K大于每个字典中元素个数m,近似表达时,并不是采用全部字典元素对样本进行近似,而是选取尽可能少的字典元素对样本进行近似,这样的近似方式有助于选取对织物宏观上近似,从而忽略细节部分如疵点区域,提高检测精度。但也因此造成求解系数时计算量较大,处理时间长,不能满足实时连续检测的要求。为提高后续求解系数的速度与重构图像的准确度,本文对稀疏字典进行优化处理,主要从2个方面入手:子窗口尺寸和稀疏字典的优选。
2.2.1 子窗口尺寸
本文所用算法1个子窗口即为1个样本,子窗口的尺寸是影响检测结果非常重要的参数。如果子窗口过小,则不能包含完整的织物纹理信息,但是疵点却可被突出;如果子窗口过大,虽然有利于刻画织物纹理信息,但是子窗口中疵点区域占比会减小,影响检测效果。
本文所用图像大小为512像素×512像素,实际尺寸59.5 mm×59.5 mm,分辨率约为218像素/(2.54 cm)。 选用32像素×32像素(实际尺寸3.71 mm×3.71 mm),16像素×16像素的子窗口大小对不同种类疵点进行测试,结果如图3所示。

图3 不同种类瑕疵不同子窗口大小的检测效果Fig. 3 Detection results of different types of defects and different patch sizes.(a)Detection result of warp defect; (b)Detection result of weft defect; (c)Detection result of blocky defect
以上检测结果表示,32像素×32像素对不同种类瑕疵检测效果比较理想。对于16像素×16像素大小的子窗口,瑕疵区域被切割到多个子窗口中,从而丢失了疵点纹理信息,导致检测效果较差。对于未知织物品种,疵点大小和分布区域随机,32像素×32像素的子窗口可保证不会将同一区域疵点分割开,最大程度地保留瑕疵信息。
2.2.2 稀疏字典优选
由于稀疏字典通常采用过完备字典进行信号表征,其字典的数量及稀疏化程度直接决定了系数编码的求解时间。为此,本文采用对稀疏字典库进行分组优化策略实现其求解时间效率的提升,具体是通过对稀疏字典库和分组字典数量的优选实现。
1)稀疏字典库。首先需要确定稀疏字典的大小K值,稀疏字典通常为过完备字典。由于本方法是要挑选部分组合,因此稀疏字典K无需过大,满足所需即可。在子窗口大小为32像素×32像素,K分别为128,256,512,1 024,1 248时,测试重构误差,结果如图4所示。
从图4可看出,当K=512时重构误差变化幅度明显降低,且能满足挑选组合所需,因此稀疏字典大小定为K=512。
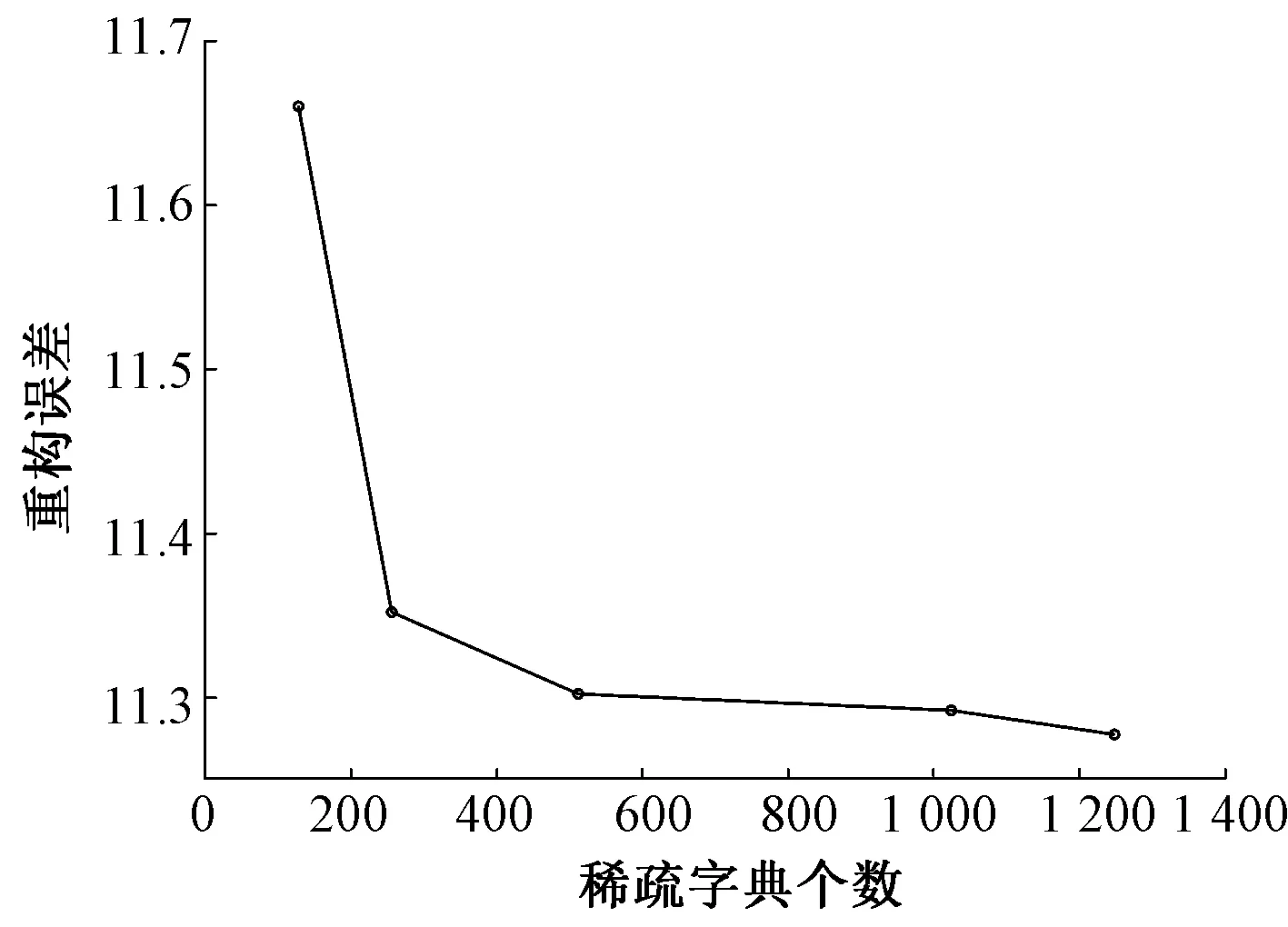
图4 K的大小与其对应的重构误差Fig. 4 Size of K and its corresponding reconstruction error
2)分组字典优化策略。稀疏字典个数确定后,为保证分组的效率及每个组合对织物图像的重构效果,每组字典中k的个数选择同样是重点。
从理论上讲,k增大有利于还原图像的组织纹理,减小近似误差,但另一方面,如果k过大,就很可能将疵点区域引入字典原子中,使得疵点部分也能很好的近似还原,影响检测效果;而且k增加,系数的求解耗时会越长,影响检测效率。
此时,对512像素×512像素的白坯布进行测试,优化字典个数k与重构误差的关系如图5所示。
从图5中可以看出,随着优选字典个数k的增加,重构误差会随之减小,即原织物图像的近似效果越好。对于不同子窗口大小,在字典个数k=10之后,k增加而重构误差减小的幅度已经不大,至k为12~14时趋于稳定。为综合考虑检测效果与速度,选择k=14。
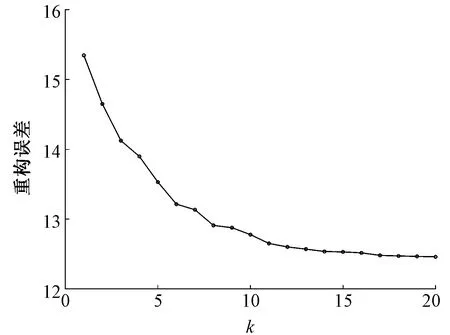
图5 k的大小对重构误差的影响Fig. 5 Influence of k on reconstruction error
综上所述,从字典库中优选其中的14个字典就能对织物纹理实现很好的近似,但其优化过程耗时较长。为此,本文提出一种分组字典优化策略提升算法时间效率,其算法流程如下。
Input: 图像Y,字典D,分块提取Y中所有样本Yp
1: 初始化Di=Ø,i=0
2: 按顺序分组每组14个字典基,找出整体重构误差最小的组合得到初始字典D0
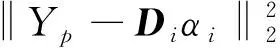
4: repeat
5: 输入上一周期更新过的Yp
6: repeat
7: 从D中随机挑选14个字典基
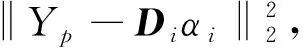
10: 添加Di到Ds,i+1
11: untilYp=Ø
Output:字典集合Ds
首先输入正常图像Y和稀疏字典D,将图像划分子窗口提取所有样本。然后挑选初始字典,将原稀疏字典按顺序分组,每组14个字典基,超出部分去除。用每个字典组合对所有样本进行重构,选择图像整体重构误差最小的组合,即初始字典组合D0。之后更新其它字典组合,设置重构误差界限L,用Di(i=0,1,2,…,n-1)对所有样本进行重构,重构误差超出界限L的样本留待下个周期,每个周期选择1个Di加入字典库集合Ds,直至所有样本都能够被很好的表达。
加入Ds的判断依据如式(6)所示,Di能很好地重构部分样本则加入,若所有样本的重构误差都超过L,则Di需要重新挑选,Di的挑选方式为从稀疏字典D中随机选择14个字典基(初始字典不在其内)。
(6)
式中:Ds为优选字典库;L为重构误差界限;1代表加入;0为重新挑选。
具体分组字典优化策略的流程见表1中伪代码算法描述。
如表1中算法所述,初始字典能够近似大部分样本,经过不断选择更新,所有样本都能够很好的近似。多个字典组合之中有重叠部分,即包含相同字典基,并且对样本的近似能够达到互补的效果。
3 实验结果与分析
本文实验所用的白坯布来自生产线,基本组织为平纹,疵点主要有断纬、断经等断疵,也包含棉结、竹节、破洞、双经和油污等疵点。为评价算法对疵点的检测效果,采用2个指标:检出率(P)和误检率(E)。
(7)
(8)
式中:Np为瑕疵样本被正确检测出的个数;Ndf为瑕疵样本的总个数;Ne为正常样本被误检为瑕疵样本的个数;Nnf为正常样本的总个数。
本文视每个窗口为一个样本,在上文已经讨论过窗口大小对检测效果的影响。为保证图像中瑕疵区域不被分割到边缘以影响到算法的检测效果,测试时,选用窗口大小为32像素×32像素。一张图像大小为512像素×512像素,可划分256个子窗口,即256个样本,图像划分子窗口样本如图6所示。

图6 子窗口样本的划分图像Fig. 6 Image of patch divided samples
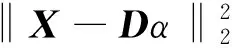
平纹白坯布总计125张(其中含疵点图像25张,正常图像100张),子窗口样本总计32 000个,对其用3种不同方法进行测试,并统计实验结果。含疵点实验图像分为3大类,分别是经向瑕疵的图像(J1~J13)、纬向瑕疵的图像(W1~W6)和块状瑕疵(K1~K6)的图像。
各方案参数:无约束字典的字典个数为14;稀疏字典的字典个数为512,正则化参数λ=0.6;优化稀疏字典包含24组,每组14个字典。
3种方法综合对比结果如表1所示,疵点检测实验结果统计如表2所示。
从表1汇总的数据可看出,稀疏字典算法耗时非常长,优选稀疏字典算法次之,无约束字典耗时最短,其中算法耗时只计算输入图像到输出是否为疵点图像结果的检测用时,不包含字典学习过程耗时及优选字典的时间。稀疏字典算法1张图像平均耗时10 812 ms,无约束字典算法平均1张耗时 32 ms, 优选稀疏字典算法为208 ms。优选稀疏字典和无约束字典在时间上都可以满足实时检测的要求。稀疏字典的检出率最高,优选稀疏字典次之,无约束字典最低。误检率无约束字典最高且与其余二者相差较大,优选稀疏字典略高于稀疏字典。

表1 不同字典方案检测效果对比Tab. 1 Comparison of three defect detection methods
从表2的统计结果可以看出,3种字典学习算法对于平纹白坯布的各种类型瑕疵都有比较好的检测效果,检出率都在90%以上。本方法对于经向瑕疵如断经、竹节等检测效果优秀且稳定,对于纬向瑕疵仅有个别图像的检测效果较差。油污、破洞和杂物等块状瑕疵由于灰度区分明显,绝大部分都可完全检出。
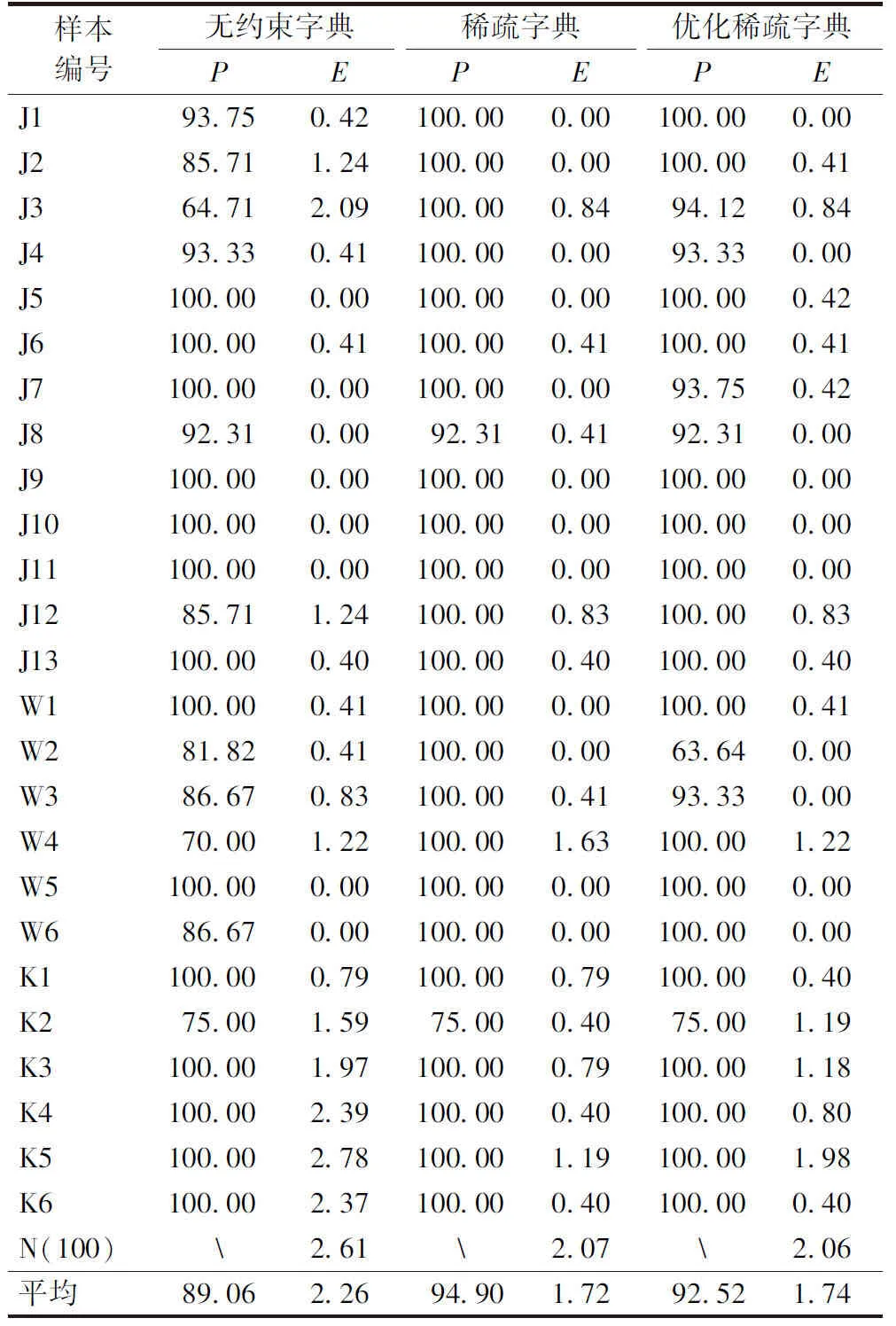
表2 织物疵点检测结果汇总
综上所述,就检测精度而言,无约束字典检测精度较差,稀疏字典检测精度最佳,优选稀疏字典的检测精度介于二者之间。优选后的稀疏字典库能在保证稀疏字典算法检测精度的情况下,节约大量时间,证明了本算法的有效性和实时性。
4 结 论
本文采用分组优化策略对学习所得稀疏字典进行分组优选,通过学习多组互补字典解决不同样本的最优近似,在大幅缩短时间的情况下更准确地突出疵点部分。结果证明本方法能够综合普通字典学习耗时短和稀疏字典学习精度高的优点,在保证实时性和低误检率的同时具有较好的检测效果,且对不同类型的瑕疵有较强的适应性,尤其对经向瑕疵具有较高的准确率和稳定性。

