梯形引水渠道不同弯曲度的水流特性分析

闫 科

(新疆伊犁河水利水电投资开发(集团)有限公司，新疆 乌鲁木齐 830000)

引水渠是水利工程中的重要渠道构筑物，起着输送水源、引水发电、农业灌溉等作用。在设计引水渠的断面形状时需要考虑地形因素、地质条件等，不过最常见的仍是梯形断面。针对梯形引水渠道施工与运营的问题，众多科研工作者通过理论解析法、有限元法、室内试验法、现场监测法等不同手段，展开了一系列的研究。周蔚蔚等[1]以某梯形引水渠为研究对象，通过COMSOL数值软件建立梯形渠道模型，系统探讨了不同断面尺寸对渠道冻深、冻胀变形及应力等影响，明确了合理梯形渠道断面尺寸以提升渠道的抗冻胀性。肖旻等[2]在Winkler地基梁理论的基础上，同时考虑了冻土与渠道接触面作用，建立了梯形渠道弹性冻土地基梁挠曲线方程。通过假设板间连续性和引入实际边界条件求解了该方向。以实际梯形渠道为例，分析了渠道不同截面的冻胀位移、表面应力以及冻结李。王功[3]首先提出对边坡系数与渠道断面尺寸相关关系的研究中存在的问题，对此，基于导数求导手段，求解获得了梯形渠道水力最佳断面函数。对函数进一步探究，准确分析了边坡系数与渠道宽深比的关系，明确了不同条件下的水力最佳断面。刘裕[4]以喀什噶尔河灌区阿瓦提干渠为研究对象，基于渠道衬砌结构冻胀破坏机制，建立了其力学模型，求解获得梯形渠道的冻胀力和冻胀位移。进一步明确了所建立的力学模型与土体参数无直接关系。欧祖贤等[5]推导出渠道壁面加糙下岸边流速系数方程，并对截面尺寸、水流流速等因素的影响规律进行系统探讨。研究表明，岸边的流速系对渠道流量有显著影响。宋禹德等[6]建立梯形渠道分流量方法，分析了主渠分水口水流形态。并通过分流试验分析了分水口水头损失规律和水面变化规律。基于某梯形引水干渠，通过有限元软件建立三维数值模型，对比了4种弯曲度(15°、45°、60°和90°)下的水面线分布、水流流速等，总结了渠道弯曲度对水流流动特性的影响规律。

1 工程概况

本文所研究的某引水干渠，全长1287m，设计流量为每秒2.22m3，是该地区引水干渠中重要的一条引水渠道。渠道横截面呈“倒梯形”，渠深2m，渠底宽2.9m，上口宽4.2m，渠底衬砌厚度12cm、渠坡衬砌厚度为12～10cm，混凝土标号为C25，抗冻标号为F100，抗渗标号为W6；渠底、渠坡垫层置换厚度取值均为50cm；渠道每3.3m设一道横向伸缩缝，伸缩缝缝宽1.5cm，采用聚乙烯闭孔泡沫板夹缝，缝内表层(过水面)灌注厚2.5cm聚氨酯密封胶防渗。

2 三维数值模型

参考该引水干渠的实际尺寸，建立了截面为“倒梯形”的弯曲干渠，梯形上宽4.2m、底宽2.9m、高度2m，弯曲处曲率半径为8m，渠道直线段均为20m，三维数值模型如图1所示。

图1 三维数值模型图

为研究弯曲度的影响，分别建立了4种弯曲度α工况：15°、45°、60°和90°。用四面体对模型进行网格划分，15°工况下共划分了8512个网格、48215个节点；45°工况下共划分了9621个网格、53251个节点；60°工况下共划分了10628个网格、60012个节点；90°工况下共划分了10723个网格、60158个节点。进口处水流流速设为1.71m/s，水体自由流动。

3 计算结果分析

根据计算结果可知，水流在进入直线段已处于稳定状态，不同工况下水体流入弯道的条件相同。凹岸侧水流流速低于凸岸侧水流流速。

水面线分布随观测点距凹岸的距离的变化曲线如图2所示。

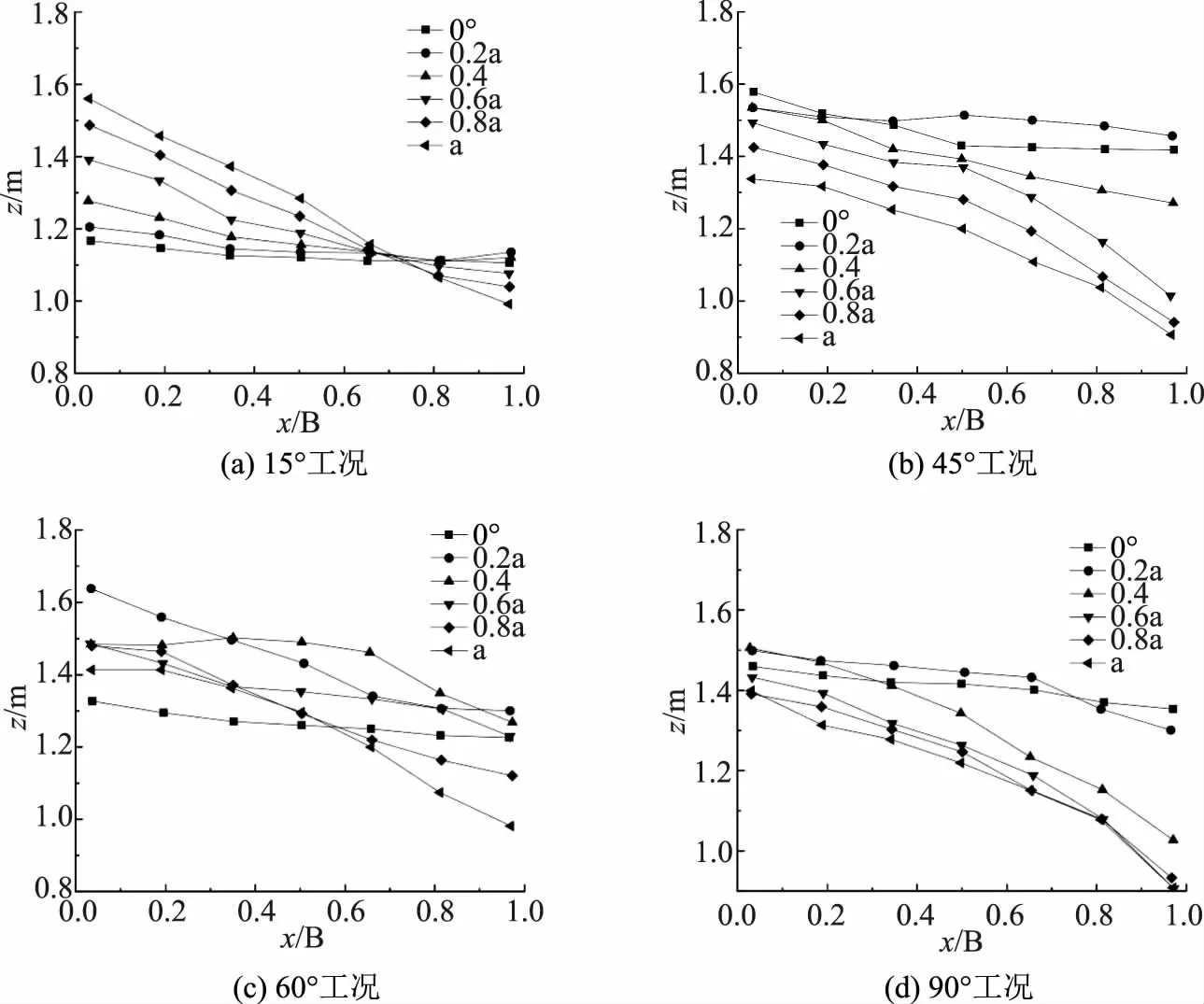
图2 水面线分布随观测点距凹岸的距离的变化曲线

对横坐标距离进行无量纲化处理(以水面线总宽度对其进行无量纲化)。每种弯曲度工况下分别给出6个特征断面结果。每种弯曲度工况下不同特征断面的水深结果见表1。从图中可以看出，由于干渠弯道的存在，水流产生了壅水现象，即水面由凸岸向凹岸逐渐抬高。对比4个弯曲度工况可知，不同弯曲度工况下特征断面水面线变化规律存在显著差别。随着渠道弯曲度减小，壅水现象发生位置逐渐向下游移动。且最低水深出现的位置始终为在弯道出口处，而最大超高水深发生的位置向弯道出口处靠近。从表中可以看出，4中弯曲度工况下，最大超高水深基本都发生在凹岸1.6m水位的位置，可见，最大超高水深受渠道弯曲度的影响有限。

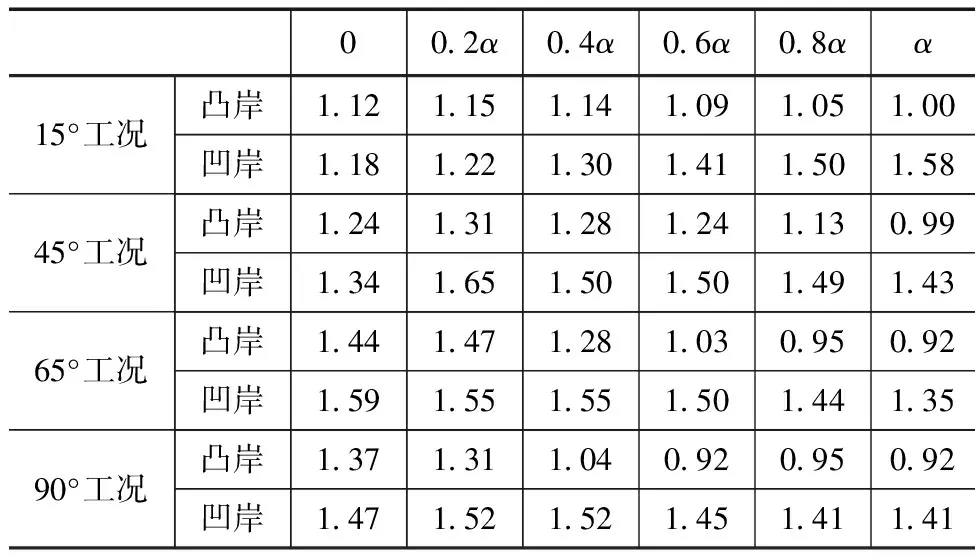
表1 不同特征断面的水深结果

弯道中心位置的垂线流速随水深的变化曲线如图3所示。

图3 弯道中心位置的垂线流速随水深的变化曲线

纵坐标水深进行无量纲化处理(以直线段水深平均值对其进行无量纲化)。每种弯曲度工况下分别给出6个特征断面的变化曲线。从图中可以看出，不同工况下的垂线流速沿水深先缓慢增加，随后保持稳定，最后在靠近渠道底部处迅速减小。具体的，水流流速最大值基本都发生在z/H为0.7附近；z/H处于0.7～1.0范围内，水流流速基本缓慢增大；z/H处于0.4～0.7范围内，水流流速基本都处于稳定状态；z/H处于0～0.2范围内，水流流速基本都显著减小。

当渠道弯曲度为15°时，水流发生的壅水现象不太明显，水流流速随着特征断面角度增大而逐渐增大。随着渠道弯曲度的增大，水流发生的壅水现象逐渐明显，水流流速随着特征断面角度的变化无明显规律。水流最大流速随渠道弯曲度的增大而逐渐减小，弯道前半段的水流流速随渠道弯曲度的增大而持续减小，弯道后半段的水流流速随渠道弯曲度的增大而持续增大。除渠道弯曲度为15°工况的流速峰值发生在弯道进口断面，其余弯曲度工况的流速峰值发生在弯道出口断面。这是因为当渠道弯曲度增大时，弯道内水流受受壁面作用增大，水流受阻水位抬升现象愈加明显，并且壅水现象发生位置逐渐向上游移动，因而水流整体流速处于减小状态，弯道入口处水流流速也减小。水流的壅水现象逐渐向上游移动导致弯道后半段发生落水现象，因而弯道后半段水流流速变大，并再弯道出口位置达到峰值。

不同观测断面0.5m水深的水流流速随观测点距凹岸的距离的变化曲线如图4所示。

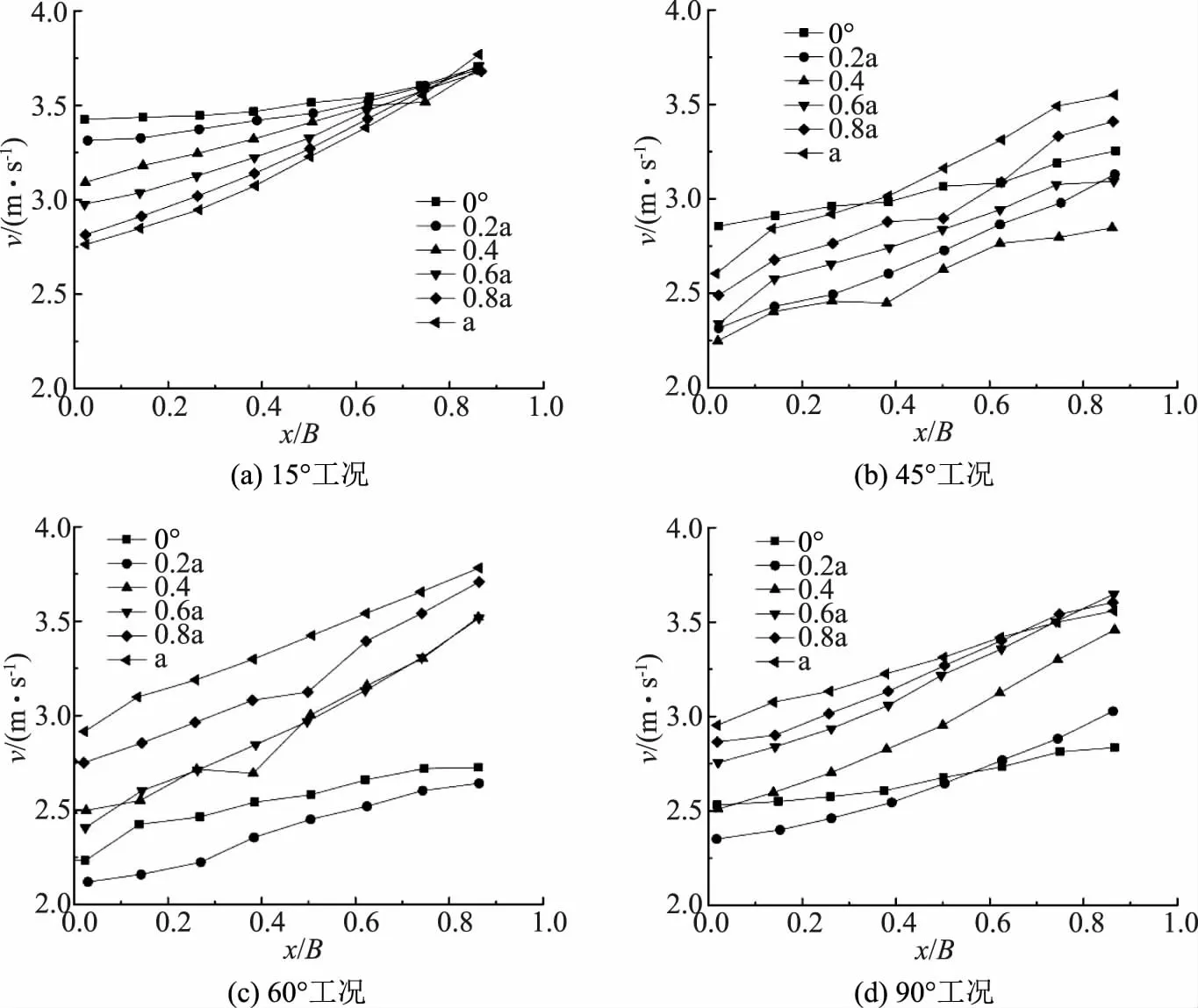
图4 水流流速随观测点距凹岸的距离的变化曲线

横坐标距离同样进行无量纲化处理。每种弯曲度工况下分别给出6个特征断面的变化曲线。从图中可以看出，不同弯曲度工况下主流都有远离凹岸向凸岸移动的趋势，即凹岸侧水流流速小于凸岸侧水流流速。但两侧水流流速在弯道入口位置接近。当水流流进弯道范围内，两侧水流流速在壁面作用下差距逐渐变大，主流靠近凸岸一侧。水流在流过弯道顶后，凸岸一侧的流速继续增大并达到峰值。这是因为水流流进弯道范围内，凹岸一侧水流产生壅水现象导致水位抬升，凸岸一侧水位降低，水位抬升区域内的水流流速低于水位降低区域内的水流流速，而水位抬升区域内的水流挤压主流致其在弯道入口处产生向凸岸一侧移动的趋势，在弯道出口处，主流受凹岸区域内抬升水位的挤压流速进一步加大。

4 数值与监测结果对比

选取引水干渠某弯曲度约为45°位置的水流监测结果与数值模拟弯曲度为45°工况的计算结果进行对比。7个观测点10cm水深处的水流流速的对比曲线、弯道入口和出口2处对比结果如图5所示。

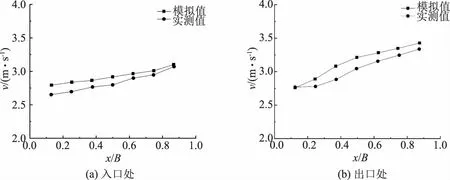
图5 监测值与计算值对比曲线

从图中可以看出，弯道范围内水流流速的监测值与计算值吻合较好，很好的证明了本文所建立模型的正确性。同时实际的水流流速略小于计算的水流流速，这可能是因为引水干渠存在少量沙子，阻碍水体留点，导致实际水流流速较低。

5 结论

(1)由于干渠弯道的存在，水流产生了壅水现象，即水面由凸岸向凹岸逐渐抬高。且最低水深出现的位置始终为在弯道出口处，而最大超高水深发生的位置向弯道出口处靠近。

(2)垂线流速沿水深均先缓慢增加，随后保持稳定，最后在靠近渠道底部处迅速减小。小弯曲度干渠的流速峰值发生在弯道进口断面，大弯曲度干渠的流速峰值发生在弯道出口断面。

(3)不同弯曲度工况下主流都有远离凹岸向凸岸移动的趋势。弯道范围内两侧水流流速在壁面作用下差距逐渐变大，主流靠近凸岸一侧。水流在流过弯道顶后，凸岸一侧的流速继续增大并达到峰值。

(4)由于模型中采用了近似于渠道空流的状态，因此模型仅适用于刚开闸通水阶段。