道路下伏软岩巷道空区稳定性模型试验研究

马晓松，崔文杰，谷存雷，杜 冰，于海洋，庄培芝

(1.山东高速菏泽发展有限公司,山东 菏泽 274000;2.济南市市政工程设计研究院(集团)有限责任公司,山东 济南 250102;3.山东大学齐鲁交通学院,山东 济南 250002; 4.鲁南高速铁路有限公司,山东 济南 250102;5.山东高速青岛产业投资有限公司,山东 青岛 266061; 6.山东高速岩土科技有限公司,山东 济南 250013)

我国煤炭等矿产资源丰富且分布广泛。长期以来,由于非法开采、过渡乱采等原因,大量开采空洞(即采空区)遗留在矿山和地下,成为制约煤炭资源进一步开采以及影响周边公路等基础设施建设和正常运营的主要危害之一[1-5]。随着我国路网的不断延伸和加密,越来越多的道路工程不可避免地要穿越采空区[6]。受施工扰动、道路结构(路基路面及桥隧等)荷载和行车动载等往复作用,采空区在部分地区可能出现“活化”,上覆岩层随之产生变形、离层、裂缝甚至破坏垮落,进而在地表形成沉降盆地并伴随裂缝和陷坑,严重威胁道路的服役性能和安全运营。国内外穿越采空区公路、铁路及建(构)筑物的破坏实例常有报道[7]。

稳定性是含采空区地层及上覆工程建设安全分析与评价的重要内容,通常采用理论分析、数值模拟和室内外试验等方法开展研究[8-9]。其中,室内模型试验是揭示含采空区地层失稳机理最为直观的手段之一。国内外学者采用离心模型试验和缩尺模型试验对空洞的塌陷过程和机理进行了大量研究。Al-Tabbaa等[10]基于缩尺模型试验研究了下伏多个土洞地基的稳定性。Abdulla和Goodings[11]运用离心模型试验模拟空洞上方弱固结砂层的坍塌破坏与空洞尺寸、砂层强度和厚度以及上部荷载的关系。程跃辉等[12]通过相似模型试验模拟路堤的塌陷过程,发现路堤下方空洞的宽度对于路堤失稳的影响很大。李明等[13]针对软、硬岩体沉陷变形规律应用模型实验方法探索煤层开采后顶板沉陷的变化规律,为评价采空区沉陷稳定提供了依据。刘庭金和李元海[14]基于室内模型试验研究了矩形空洞的渐进破坏全过程以确定内含空洞的地基承载力。Kiyosumi等[15]通过离心模型试验开展了大量含矩形空洞的坚硬土层上方条形基础承载力的研究。上述试验研究为含空洞地层的稳定性分析提供了物理依据,但道路与下伏采空区的空间交互形式复杂,相关试验数据仍相对不足,例如对于不同偏心荷载作用下的含采空区地层稳定性规律的试验研究鲜有报道。

针对以上问题,本文设计开展了地表荷载作用下软岩巷道空区稳定性缩尺模型试验,基于加载-位移曲线和地层颗粒位移观测数据,研究了不同埋深比(即,采空区顶部到地面的埋深与采空区自身高度的比值)和偏心距情况下含空区地层的稳定性演化规律,可为道路下伏采空区安全评价和加固设计提供可靠的试验数据支撑。

1 模型试验材料与装置

1.1 相似比设计

本次模型试验结合山东省原五寺庄煤矿采空区下伏正方形巷道开展工况设计。地质勘测报告显示:该区域巷道空区平均高度约为5 m,自下往上依次覆盖5 m～10 m 厚的强风化砂岩与风化页岩层和10 m～15 m厚的中粗砂层。为保证试验模型与工程原型的相似性,参照文献类似试验[16],确定各相似比尺之间关系见式(1):

Cσ=CLgCρ

(1)

其中,Cσ为强度相似常数;CL为几何相似常数;Cρ为密度相似常数。

综合考虑试验可行性和成本等因素,本次模型试验几何相似常数采用CL=1/50(模型/原型)。据此,模型试验巷道(正方形)高度为0.1 m。上覆道路荷载采用刚性压盘施加均布荷载,压盘宽度为330 mm。模型试验上覆砂层厚度设定为200 mm;采空区巷道上覆岩层厚度分别为100 mm,200 mm以及600 mm,以研究巷道埋深比对地层稳定性的影响规律。

结合文献类似试验的推荐取值[17],本实验密度相似常数为Cρ=ρm/ρp=1/1.2(模型/原型);强度相似常数为Cσ=1/60(模型/原型)。依托工程及相似材料参数见表1。

表1 原型与模型试验参数

1.2 试验材料及物理性质

本次实验设计采用PIV(Particle Image Velocimetry)颗粒追踪技术对采空区地层失稳变形规律进行量测。考虑PIV技术对表面颗粒可辨识性、分布及数量等表征条件的特殊要求,通过反复比选试验,选定采用石膏粉(选用细度模数为200目、初凝时间约为2 h的黄氏建材石膏粉)作为胶结材料进行相似材料配置。综合考虑相似材料参数设计要求(如表1所示)以及浇筑过程中施工和易性的影响,依据文献[18]实验数据,最终选取相似材料配合比为:集料粗细比=1∶0.3,砂膏质量比=3∶1,水灰比=0.55∶1。上层中砂层采用产于泰安市的硅质干砂,其中值粒径d50为0.705 mm,不均匀系数Cu为2.874,曲率系数Cc为1.407,最大和最小干密度分别为1.745 g/cm3和1.386 g/cm3。

1.3 试验模型槽

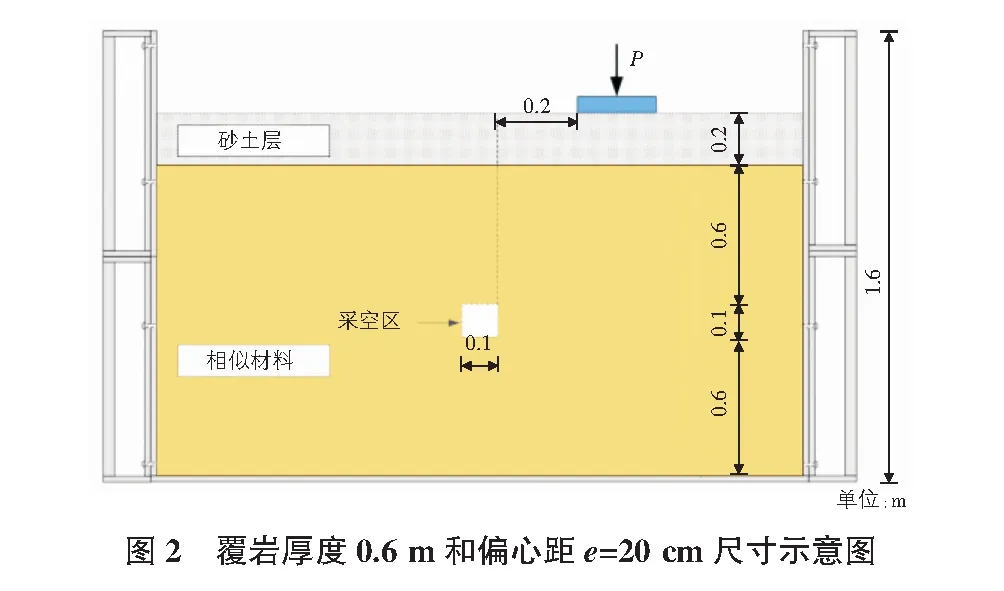
为直接观测采空区地层变形发展规律,本次模型试验在自制的二维可视化试验装置中开展,如图1所示。为减小模型试验侧边界尺寸效应的影响,取模型槽宽度为2 m(即加载板中心距模型槽侧边界最小距离不小于其宽度的5倍,巷道中心距模型槽侧边界最小距离为其宽度的10倍);为减小模型试验底边界尺寸效应的影响,同时减少试验工作量和材料消耗量,设计模拟巷道底边距模型槽侧底边最小距离为其高度6倍(即0.6 m)。据此,模型槽尺寸为2 m(长)×0.3 m(宽)×1.6 m(高),上部设置带双向导轨的反力横梁,整体由钢板加工焊接制成;为便于观测分析,模型槽前侧为钢化玻璃结构;另有一套伺服加载系统(下雨加载板用球铰连接)和数据采集系统(见图2)。

2 模型试验设计与流程

2.1 试验工况设计

本次模型试验旨在探究巷道空区埋深比和地表偏心加载对空区地层失稳及变形的影响规律。正方形巷道空区高度h为10 cm,取巷道上覆岩层(相似材料)厚度H分别为10 cm,20 cm以及60 cm;将加载板边缘距巷道中心水平距离定义为偏心距e,试验设置三种偏心距:e=0 cm,e=10 cm和e=20 cm。因此,本次试验共设计9种工况。

2.2 试验制样

石膏砂浆相似材料搅拌完成后,在定制模具中浇筑成型;根据试验工况设计,采用10 cm×10 cm的方形钢管位置预留巷道(如图3所示)。浇筑过程中使用振动棒对模具箱中石膏砂浆进行振动,以排除内部气泡保证砂浆密度均匀,并防止石膏砂浆凝固。浇筑完成后将上表面刮平,养护24 h后拆除顶板,而后将模具箱通过导轨推至模型槽内部。

相似材料模具箱与模型槽固定后,采用雨淋法进行上覆砂层的制备(见图4)。为减小模具箱侧壁对砂层的摩擦阻力,在模具箱底板与两侧板铺设具有低摩擦系数的特氟龙塑料纸[19-20]。本次试验采用漏沙孔孔径为15 mm,淋砂高度为200 mm,最终测得淋砂密度为1.6 g/cm3;依照上文测得砂的最大与最小干密度,计算得相对密实度Dr=65.1%,属于中密砂;根据JTG 3430—2020公路土工试验规程进行直剪试验测得此密度下干砂的内摩擦角为41.7°。

2.3 试验加载与测试

上覆荷载采用高精度伺服千斤顶施加,千斤顶顶部安装在上部反力梁上,通过在千斤顶底部安装压力分散装置将荷载均匀施加到地基表面。加载设备上配置压力传感器与拉线位移传感器,分别测量加载压力与竖向移动位移(采用间隔:0.1 s)。为防止加载速度过快产生“加速度效应”,试验选用试验速度为2 mm/min[21]。

为获取加载过程土体颗粒实时位移数据,采用佳能1500D型号数码相机对透明观测窗(并在观测窗上标记基准点,如图5所示)进行连续拍照(拍照时间间隔为5 s),对应照片尺寸为6 000×4 000像素。为保证照片质量,试验过程采用白色补光灯提供稳定光源。

关键试验流程包括:控制系统进行初始值清零,将承载板缓缓下降至与砂层轻轻接触,系统接触力值不大于0.5 kN;开启并设置观测系统后,运行程序开始试验加载;当荷载位移曲线出现较为明显转折后,停止加载并保存试验数据,控制相机停止拍摄;将承载板上升至足够高处并拆除相机与补光灯等拍照设备,回收砂层内大部分干砂,结束试验。

3 试验数据与分析

3.1 荷载-位移曲线特征

图6和图7为巷道位于加载板正下方和偏心距时e=0.1 m,不同覆岩厚度工况下荷载位移曲线。本次模型试验荷载-位移曲线均呈现类似特征,即:地表位移随着荷载增大近似呈现线性增加(类弹性响应阶段),且所有工况该阶段曲线斜率相近;位移达到一定幅值后,荷载-位移曲线斜率逐渐降低,即逐渐进入弹塑性响应阶段;随后,达到极限荷载值,荷载位移曲线发生突变,呈现脆性破坏特征。另外,图6和图7显示:采空区上覆地层极限承载力与破坏时沉降位移均随采空区上覆岩层厚度增大而增大,分析其内在原因是由于本文试验工况的破坏模式主要为地表加载引起的浅层空区塌陷伴随的地层失稳破坏。随着采空区上覆岩层厚度的增大(即采空区埋深变大),采空区赋存对地层承载能力的影响变小,因此地层极限承载力增大,致使地层失稳破坏(即荷载传递至采空区赋存位置)所需要的地表变形变大。

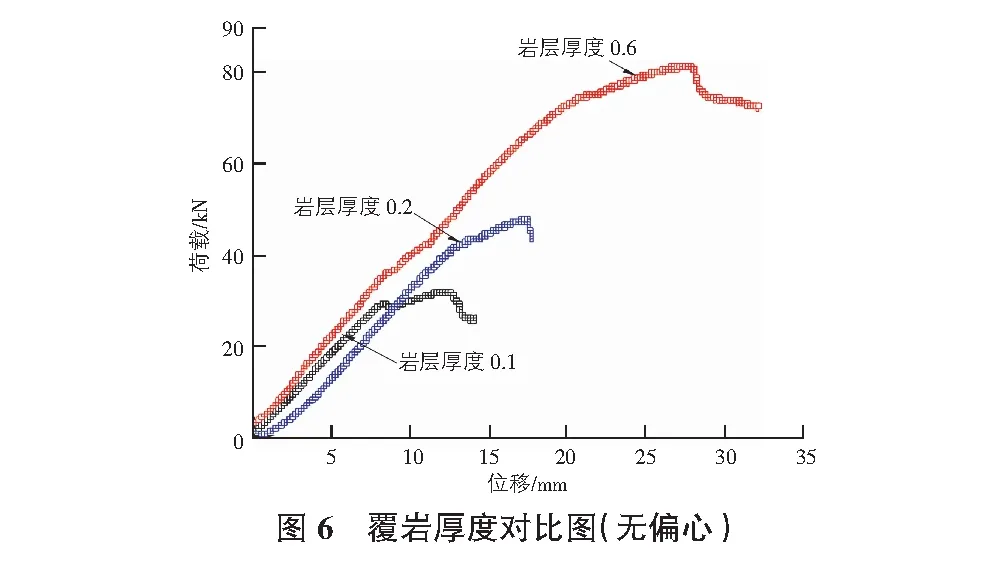
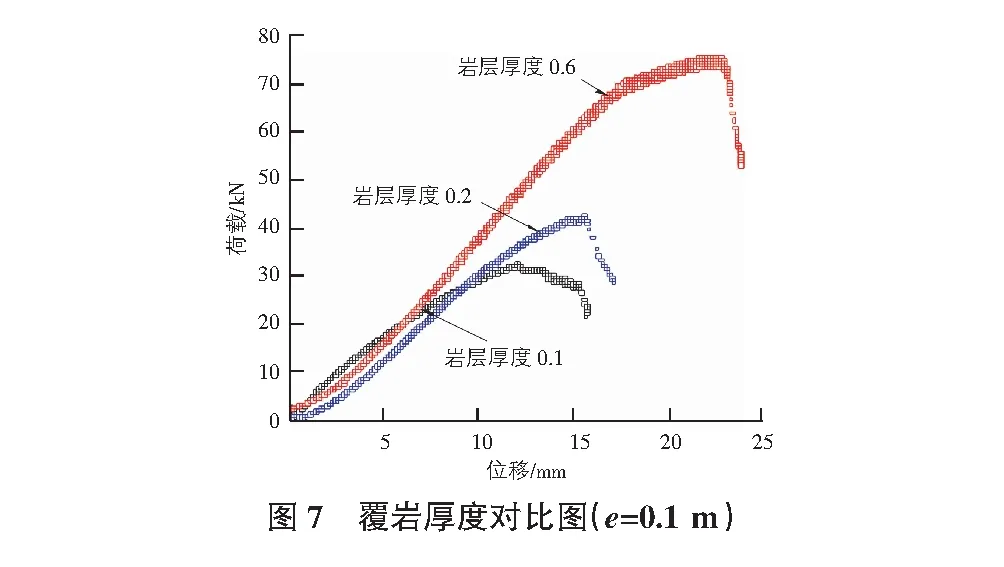
图8为不同偏心状况下,破坏时刻地表沉降值随采空区上方覆岩厚度的变化趋势。结果显示:覆岩厚度相同时,无偏心工况在破坏时刻地表沉降值大于偏心加载工况,且不同偏心加载工况下破坏沉降值的相对偏差(各工况最大偏差/无偏心工况沉降值)随埋深比增大而增大。如:覆岩层厚度为0.1 m时,无偏心工况破坏时地表位移为12.21 mm,此时不同偏心状况下地表破坏位移偏差为6.3%;覆岩厚度为0.2 m时,无偏心工况破坏时地表位移为17.39 mm,此时不同偏心状况下地表破坏位移偏差为10.8%;覆岩厚度为0.6 cm时,无偏心工况破坏时地表位移为27.19 mm,此时不同偏心状况下破坏位移偏差为18.0%。

3.2 PIV位移矢量分析

采用White等[22]提出的Geo-PIV技术对连续拍摄的图片进行计算处理,可获得地层失稳时刻颗粒位移矢量图。

图9显示了无偏心情况下地层失稳时刻颗粒位移矢量图随覆岩厚度的变化规律。当覆岩厚度为1h(h为采空区高度)时:受上覆荷载影响,呈现整体式破坏模式,上部砂颗粒发生向下以及向两侧方向的位移,并沿加载位置至石膏砂浆接触面形成对称的连续剪切面,剪切面与水平方向夹角约为45°;下方石膏砂浆层出现自交界面连通至巷道空区的裂隙带,呈对称分布。随着巷道埋深(埋深比)的增大,石膏砂浆层的颗粒位移逐渐减小。当覆岩厚度为6h时,地层破坏模式呈现为浅层砂土层的压入破坏,即采空区的赋存对地层失稳模式不再产生影响。

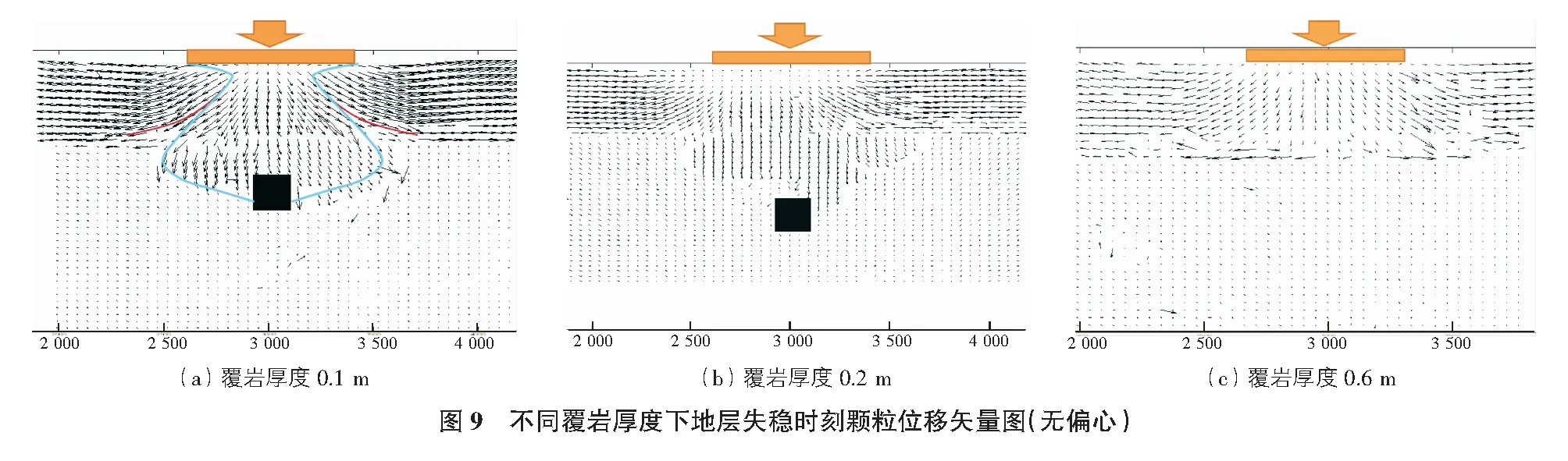
图10为覆岩厚度为1h、偏心距为1h和2h工况下地层失稳时刻颗粒位移矢量图。由图10可知,随着偏心距的增大,地层破裂面形态不再对称。在石膏砂浆层,一条破裂面由接触面连通至采空区顶端,另一条向下延伸至与采空区相似高度处后向右侧发展。当偏心距为2h时,破裂面形态受采空区的影响不再显著,此时地层极限承载力高于采空区位于正下方工况。

4 结论

本文开展了道路荷载作用下巷道空区地层承载和变形特性室内模型试验研究。基于荷载-位移曲线和全域变形特征量测数据,分析了不同巷道埋深比和加载偏心距工况下道路下伏采空区的失稳破坏特征,得到主要结论如下:

1)地表荷载作用下,含软岩巷道空区地层的荷载位移曲线呈现典型的三阶段特征:初始阶段荷载-位移曲线近似线形变化(类弹性阶段);后进入屈服阶段,荷载-位移曲线斜率逐渐降低;随后,随着位移增大,荷载跌落,呈现脆性破坏特征。

2)地层极限承载力随采空区上覆岩层厚度的增大而增大,其破坏模式随采空区上覆岩层厚度增大逐渐由含巷道失稳的整体剪切破坏发展为上部砂土层的局部压入破坏。

3)相同覆岩厚度情况下,地层极限承载力随偏心距增大而先减小后增大;当地表荷载充分远离下伏空区后,采空区对地层承载力的影响不再显著,相关现象与剪切破裂面的大小及形状密切相关。