一种新构型变转速共轴直升机的垂向-航向辨识

王子琪

(中国直升机设计研究所,江西 景德镇 333001)

0 引言

近年来,小型无人飞行器迅猛发展,多旋翼飞行器、新构型共轴直升机等飞行器得到了诸多学者的重视。对于这类共轴直升机,不乏有通过控制旋翼转速代替控制总距,同时差动下旋翼总距角控制航向的操纵方式。这种操纵方式可以减少飞机结构零件数目,降低机体重量,但同时也带来了更加严峻的垂向-航向耦合问题。传统电动共轴直升机的旋翼转速是固定的,通过总距舵机与航向舵机的相互协调来解决垂向-航向耦合问题。与控制总距舵机相比,控制转动惯量很大的旋翼更加困难。所以建立输入为旋翼转速、航向差动,输出为垂向速度、航向角速度的耦合模型尤为必要。

国内外关于系统辨识的相关研究已有了丰硕的成果。早在1999年,学者L.Ljung[1]就对系统辨识做出了定义,并给出了系统辨识的“三要素”。杨平等学者[2]结合系统辨识的最新发展,将其补充为“六要素”,更为详尽地概括了系统辨识的所有工作。Klein等学者[3]建立了经典的极大似然辨识算法,使得辨识算法有了长足的进展。得益于系统辨识理论的快速发展,用于系统辨识的商业软件也迅速发展,如学者Tischler[4]基于频域辨识、偏相干系数分析等理论建立的CIFER软件,可以较为准确地辨识系统模型。并且,基于神经网络的系统辨识也日趋成熟;基于实时递归学习的递归神经网络也可以较为准确地辨识系统模型。学者Simon[5]在专著中详尽地叙述了应用递归神经网络进行系统辨识的理论依据。

同时,系统辨识在航空领域的应用范围也在逐渐扩大。唐炜学者[6]通过应用Morlet小波变换成功辨识了大噪声下的颤振模态参数。刘鹏、武哲学者[7]通过优化复合窗函数,对直升机状态空间模型进行了频域辨识,得到了较好的结果。Jaime del Cerro等[8]对小型直升机应用遗传算法进行了辨识,并对其动力学特征进行了分析。Michel Verhaegen等学者[9]应用子空间辨识算法对BO-105直升机的模型进行了辨识,并较为详尽地叙述了辨识的过程和数据处理。

本文对一种新构型变转速共轴直升机的垂向-航向模型进行分析。以悬停状态为基础运动,采用扫频激励进行飞行试验;结合频域辨识的理论,应用变转速共轴直升机的气动模型,对气动导数进行估计并得到搜索域;通过遗传算法对系统参数进行寻优,得到了满足时域验证的垂向-航向状态空间模型。最后,对相应的气动导数进行分析,得出了变转速共轴直升机垂向-航向操纵性与稳定性结论。

1 小型变转速共轴直升机

1.1 D-07简介

本文是以北京航空航天大学直升机研究所研制的D-07变转速共轴直升机为试验样机进行分析。D-07采用变旋翼转速操纵替代传统直升机的总距操纵控制升降,差动下旋翼桨距角控制航向,同时改变上下旋翼周期变距控制横滚与俯仰。图1为D-07的操纵系统结构示意图,相关技术已申请专利。

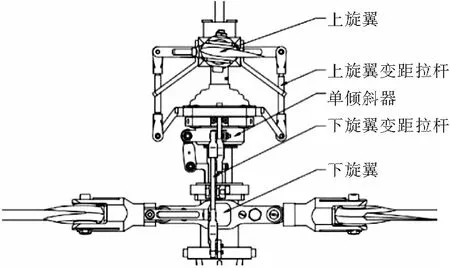
图1 D-07操纵机构示意图

D-07以其小型化、轻量化、长航时为优势,具备多任务兼容、单兵携带、边防、巡线等相关应用潜力,是一款性能出色的小型共轴直升机,其参数见表1。

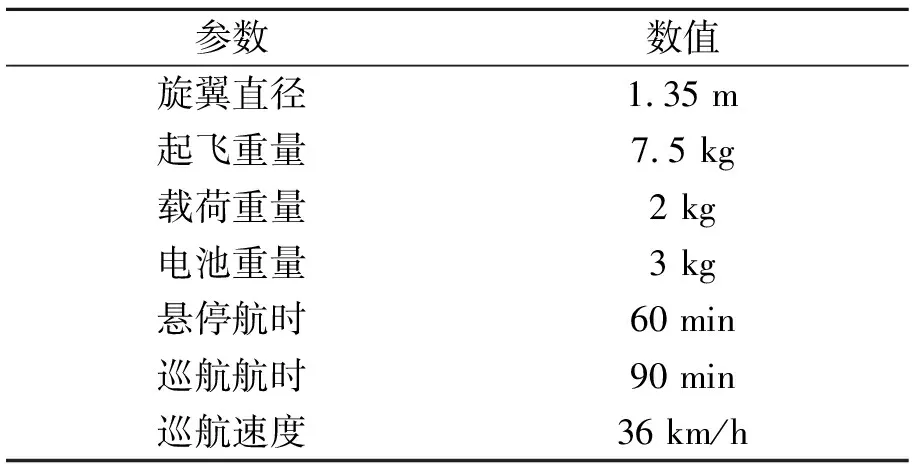
表1 D-07各项参数

1.2 垂向-航向飞行动力学模型的建立

本文采用文献[10]中的直升机线化模型,结合类似于D-07的变转速操纵对该模型进行相应的调整,并独立出以悬停状态为基础运动的垂向-航向的状态空间模型,表示如下:

y=Cx+Du

(1)

其中,m为飞机质量;Iy为飞机y轴转动惯量,Fy为机身所受y轴拉力;My为机身所受y轴力矩;Vy为垂向速度;ωy为航向角速度;Ω为旋翼转速,单位为rad/s;φ01为下旋翼航向操纵桨距,单位为rad。

为了达到对耦合项进行辨识的目的,本文不对状态空间中通常认为较小的气动导数进行预先置零处理,而是作为未知量进行辨识。

2 频域辨识

2.1 频率响应与相干函数

频域辨识理论主要包括两部分:①根据试验数据,计算系统输入-输出对的频率响应;②计算输入-输出对的相干函数,确定待辨识的频率范围。

根据维纳-辛钦定理并加以推导[11],就可以通过输入-输出对的自功率谱密度和互功率谱密度得到系统的频率响应,可表示如下:

Pxy(Ω)=H(ejΩ)Px(Ω)

(2)

其中,Pxy为输入输出的互功率谱密度,Px为输入的自功率谱密度,H(ejΩ)为系统频率响应函数,Ω为数字角频率。

相干函数是一种表征输入-输出对在各频率下线性相关度的函数,一般认为相干函数大于0.6时,数据质量较好。其计算式表示如下:

(3)

2.2 状态空间频率响应

为了求取状态空间的频率响应,需要使状态空间转换为传递函数矩阵。其计算方式可以表示为:

G(s)=C(sI-A)-1B+D

(4)

其中,针对式(1)建立的状态空间来说,G(s)为一个2行2列的传递函数矩阵。

在得到各输入-输出对的传递函数后,为了保证在遗传算法寻优时不会出现“频谱重叠”的现象影响寻优效果,需要将连续系统传递函数转换为离散系统传递函数,转换方法可以选择双线性变换法等。

3 遗传算法与气动导数估计

3.1 遗传算法

遗传算法是一种启发式搜索算法,其核心思想是将每个待优化变量转换为基因信息,并在给定的范围内,通过交叉和变异的方式进行搜索。以适应度函数表征每个基因的优秀程度,最后得到适应度函数最优的基因。遗传算法在各个领域应用广泛。其计算步骤可表示为[12]:

1)基因的初始化,根据预先知识得到搜索域,并在搜索域内均匀、随机地选取初始基因;

2)对种群中每个初始基因的适应度函数进行筛选;

3)根据适应度函数选择优秀的基因,并定义为父代基因;

4)按一定概率和分布,随机地选取两条父代基因进行交叉,产生子代基因;

5)按一定概率和分布,对上一步产生的子代基因进行变异;

6)对新的子代基因和父代基因进行适应度函数的评价,择优替换父代基因;

7)查看适应度函数是否满足迭代终止条件,如果满足,则停止,并返回最终基因,若不满足迭代终止条件,则返回第3步。

基于频域辨识的适应度函数可以表示为[13]:

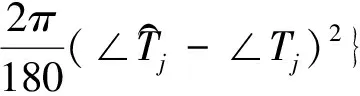
(5)

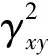
进而,遗传算法的基因可以定义为系统未知气动导数组成的向量,表示为:

Θ=

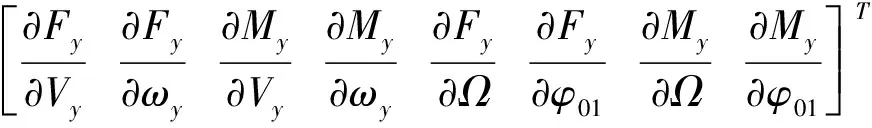
(6)

3.2 气动导数估计

使用基于启发式搜索算法的系统辨识,如果搜索域过大,极易使辨识结果陷入局部最优解。为确定搜索域,需要得到气动导数的估值。本文通过叶素法、非均匀入流、经验函数法等,对变转速共轴直升机进行建模,得到了一种针对变转速共轴直升机的气动模型;并通过对该气动模型进行数值微分,得到相应的气动导数估值。此估值可以为遗传算法的搜索域提供参考。

气动模型中,采用了McAlister等学者根据和毕奥-沙瓦尔定理得出的共轴直升机上下旋翼干扰模型[14],可以表示为:

其中,δ为旋翼干扰系数,z为待分析旋翼与干扰产生旋翼的垂向距离,常数k为经验系数,与待分析旋翼有关。

引入BEMT法得到诱导速度模型,并对旋翼各向力建立气动模型;进而对旋翼挥舞动力学进行建模,得到了桨叶挥舞运动学方程,可以表示为:

(8)

最后,联立关于14个变量组成的封闭的非线性方程组。此方程组可以表示为:

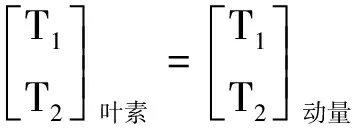
(9)

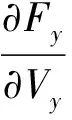
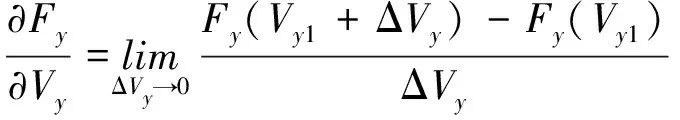
(10) )

根据上式,依次对相应的气动导数估值进行计算,得到了如下估计的状态空间模型:

(11)

为了简化计算,上述方程组为定常状态下的气动模型,忽略了各轴角速度、角加速度、各轴加速度和挥舞角加速度对气动力的影响,所以未涉及关于航向角速度的2个气动导数。

可以看出,各系数之间存在着数量级的差别,如果不对初值进行估计,盲目选取搜索域,则极有可能陷入局部最优解。并且,相比于通过单独辨识主通道传递函数来选取搜索域的方式,上述数值微分的计算方法更加简便,且无需对飞机主通道进行SISO系统辨识,仅需要应用牛顿法求解非线性方程即可。

4 飞行试验与辨识结果

4.1 飞行试验

由于运动方程中带有飞机y轴转动惯量,所以若希望对气动导数进行分析,则需要对飞机的y轴转动惯量进行实测。测量方式采用双线摆试验[16],多次重复后取均值,得到D-07空载时y轴转动惯量Iy=0.0984 kg·m2。

为满足采样定律,根据经验认为直升机主频率在0.3 Hz～20 Hz之间,所以应用50 Hz的采样频率就不会出现频谱重叠。采样设备选用机载加速度计、陀螺仪等。采用扫频输入作为激励,得到相应的试验数据,进行辨识工作。图2为D-07飞行试验图。

图2 D-07飞行试验

4.2 辨识结果

应用上述理论方法,对得到的飞行数据进行辨识。以上述估计值为参考选取初始搜索域,得到如下状态空间方程:

(12)

图3-图6为各通道辨识模型与飞行数据频率响应对比图。可以看出,辨识模型与飞行数据在相干函数大于0.6时有较好的一致性。

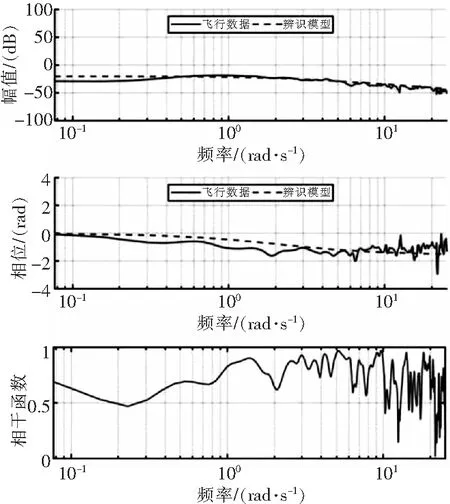
图3 Ω～ΔVz通道频率响应对比图

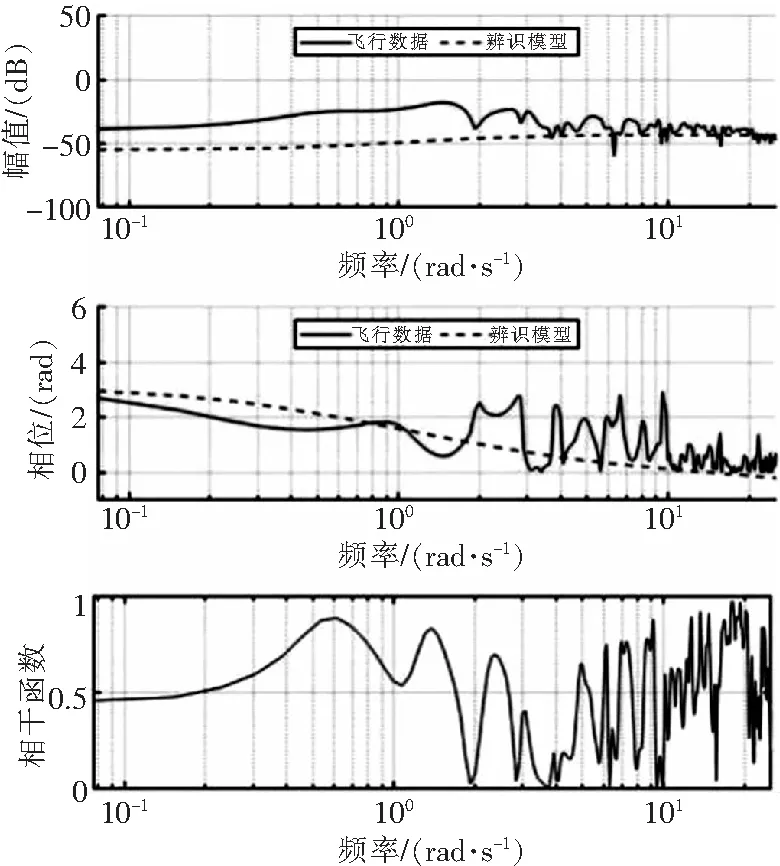
图5 φT～ΔVz通道频率响应对比图

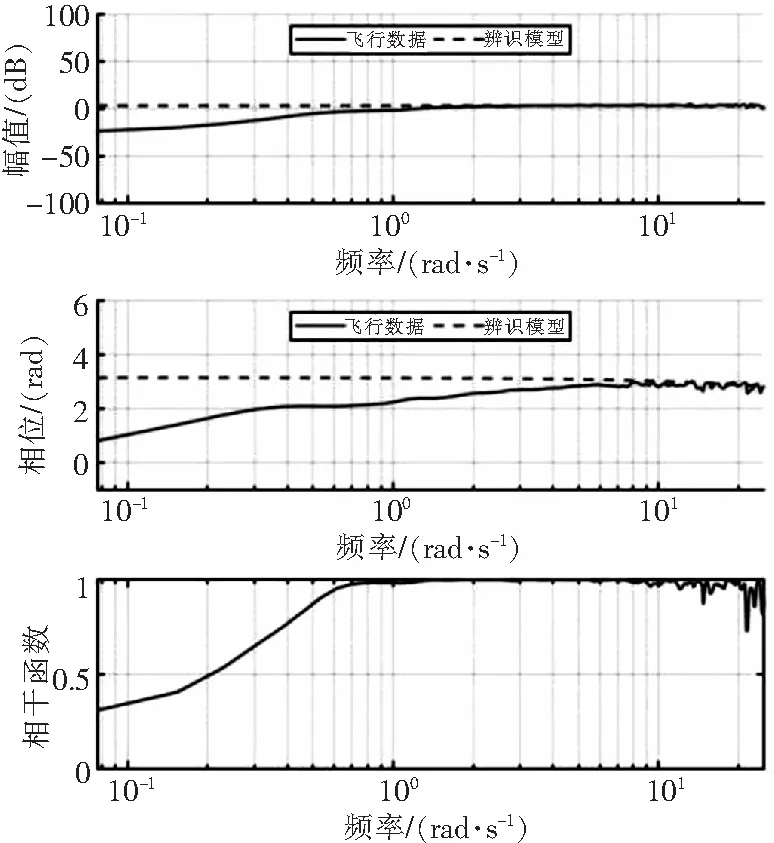
图6 φT～Δωz通道频率响应对比图

最后,需要对辨识得到的模型进行时域验证。图7为时域验证对比图。

图7 时域验证对比图

5 结果分析

得到了上述状态空间模型后,可以提取出D-07的气动导数,表示如下:

[-14.35 3.28 0.28-8.10

1.27 4.14 0.01-10.32]T

(13)

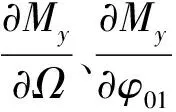
6 结束语

本文首先介绍了变转速共轴直升机的操纵形式,提出了垂向-航向存在耦合的问题。为了确定其状态空间模型,对变转速共轴直升机D-07进行气动建模,得到了悬停状态下状态空间各系数的估计值;并在悬停状态下对D-07进行了扫频飞行试验,应用基于遗传算法的频域辨识,得到了满足时域验证的状态空间模型。提取其中的气动导数值,分析了该机垂向-航向的耦合问题,以及其垂向、航向运动阻尼,并得到以下结论:

1)相比于传统共轴直升机,变转速共轴直升机的航向操纵对垂向速度有更大影响,耦合效果较强。

2)在调整下旋翼安装角且满足小扰动假设时,转速操纵对航向角速度的影响较小,一般可以忽略。

3)D-07在垂向运动和航向运动上有一定的阻尼,具有垂向、航向动稳定性。

上述结论可以为变转速共轴直升机的控制律设计提供理论依据。