具有空气流通性能声滤波器消声材料的设计与研究

陈怀军，赵文霞，翟世龙

(1.宁夏师范学院 物理与电子信息工程学院，纳米结构及功能材料工程技术研究中心，宁夏 固原 756000；2.西北工业大学 物理科学与技术学院，陕西 西安 710072)

实现负等效声学参数和基于负等效声学参数的奇异物理现象是声学超材料的主要研究目标之一.从3D核壳结构[1]演化而来的2D薄膜结构[2]和其他受局域共振思想的启发而提出的负等效质量密度模型[3]是实现负等效质量密度的主要途径；亚波长亥姆霍兹共振器在水介质中首次实现了负等效弹性模量[4]，由此亥姆霍兹共振器一直是实现负等效弹性模量的主要模型[5].在实现单负声学参数的基础上，通过耦合一种或者两种谐振单元的方式，实现了双负参数声学超材料[6].以负等效声学参数为基础，实现了一系列自然界中常规材料无法实现的声学奇异现象，例如负折射、隐身斗篷、超分辨成像、声学超常传输和声学聚焦等[7-12].

薄膜结构声学超材料在不同振动状态时具有不同声波透过率的特点，可以用来设计具有空气流通性能的消声材料.与传统消声材料相比，基于薄膜结构的消声材料在同时要求噪声消除和空气自由流通的实验室、工厂等众多噪声消除场所具有重要应用价值.传统消声材料通常采用声学硬材料将声源完全包围的方式阻隔声波传播，但在传播声波的媒质是空气的情况下，阻隔声波的方法必然会导致包围层内外的空气难以流通.在需要空气流通的噪声消除场所，为了实现空气流通的目的需要在包围波源的声学硬边界设置开放区域，但开放区域会导致声波透射，进而影响消声效果，并且声波的透射率会随着开放区域面积的增大而升高.传统消声材料无法兼顾消声和空气流通的固有缺陷，限制了其在对空气流通有较高要求的噪音消除场所的应用.

文中通过在带有空气通道的声硬壁中嵌入薄膜材料的方法设计了声学滤波器，利用滤波器的耦合共振效应将特定频率声波的透射率降低至10-3.这种声学滤波器允许空气自由流通，并且滤波器的工作频带可以通过改变薄膜结构和空气通道的几何尺寸进行调谐，用以实现宽频的噪声消除.

1 模型分析与仿真计算

1.1 模型分析

滤波器的三维和平面结构如图1所示.整体上滤波器是由局域共振薄膜、支撑、中心开有圆孔的铝板和铝板外围的环形空气通道组成的声学超材料.铝板厚度5 mm，铝板半径与环形空气通道的宽度之和为50 mm，铝板中心圆孔的半径为8.5 mm，整个滤波器由铝板边缘4个可以忽略厚度的支撑固定.铝板的中心圆孔覆盖张紧的聚乙烯薄膜，薄膜的厚度为0.04 mm，密度为920 kg·m-3，杨氏模量为6.9×109Pa，泊松比为0.36[13].当工作时，将滤波器通过支撑固定在外部环形支架上，环形支架与铝板边缘之间的环形空气通道允许空气自由流通.

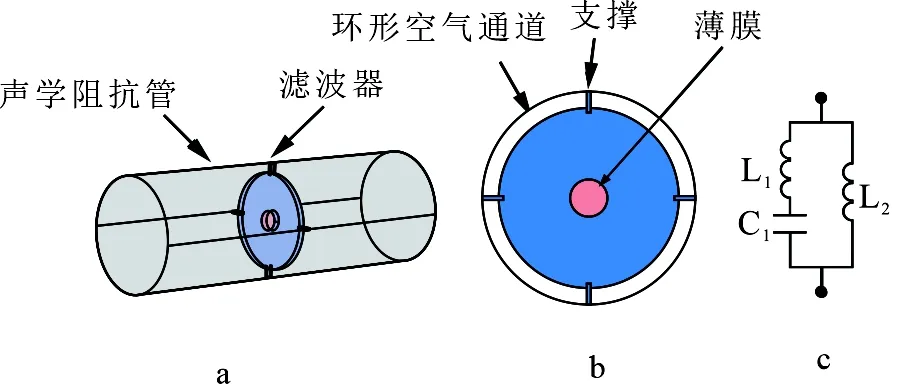
图1 滤波器构形示意图

根据等效电路理论，可以将滤波器看作是声容和声感的串并联组合，其等效电路图如图1c所示.其中，处于滤波器中心圆孔处的薄膜等效为由声感L1和声容C1串联组成，而处在外围的环形空气通道等效为声感L2[14].上述L-C谐振电路中薄膜和环形空气通道的等效阻抗值分别为

其中，ω=2πf为入射声波的角频率.由于在等效电路中薄膜和环形空气通道并联，由此滤波器整体的等效阻抗值为

1.2 仿真计算

应用COMSOL MULTIPHYSICS的频域模式对设计的声学滤波器进行仿真计算.将滤波器放置在声阻抗管的中部，声波垂直入射.对滤波器前端入射声压Pi和滤波器后端透射声压Pt进行监控.考虑到滤波器的镜像对称性，因此只需建立图1b所示的一半模型即可.

2 分析与讨论

2.1 滤波器的声场透射

对声学滤波器在3种不同状态下的入射声压和透射声压进行了仿真计算，以便详尽地展示滤波器的工作原理.为了便于讨论，固定薄膜覆盖区域的面积，即薄膜面积保持不变，并将环形空气通道缝隙的径向宽度设置为4 mm.第一种状态是滤波器正常工作的状态，此时声波在薄膜结构的反射作用下通过环形空气通道，这种状态下透射曲线如图2中实线所示(左边坐标轴).在1 194 Hz处出现了一个很窄的透射低谷，透射率接近10-3.在1 194 Hz以后，紧接着在1 218 Hz处出现一个透射峰，随着透射频率的变化，透射率保持在较高的水平.在这种状态下，中心频率为1 194 Hz的窄带声波被滤波器过滤.图2中虚线(右边坐标轴)对应滤波器正常工作状态下的反射曲线，在1 194 Hz处出现透射最小值，与反射最大值相对应，表明此时透射最弱，反射最强.为了进一步说明声学滤波器中薄膜结构的作用，设置了第二种状将薄膜关闭.此时薄膜不再发挥作用，声波正常通过环形空气通道，对应的透射曲线如图2中带五角星的曲线所示.随着入射声波频率的变化，环形空气通道的透射率基本维持在0.6左右随入射频率变化声波透射率基本不发生变化的性质与声波透过声学硬质材料边缘缝隙时的透射规律相吻合.设置的第三种状态是将环形空气通道封闭，既铝板的径向宽度为50 mm，环形空气通道的宽度为0.此时的声波透射率在薄膜结构的单独作用下产生，透射率曲线如图2中带方块的曲线所示.仅薄膜结构工作时，1 194 Hz处的声波透射率为0.52.环形空气通道和薄膜结构单独工作时均不能在1 194 Hz处形成滤波，由此可知1 194 Hz处的滤波现象是由薄膜结构和环形空气通道共同作用产生的，与(2)式中ω2的表达式物理意义相吻合.

图2 不同条件下滤波器的透射反射系数

2.2 滤波原理分析

薄膜振动时等效为次级声源，滤波器前后表面的声场是由薄膜振动产生的声场和直接通过环形空气通道声场的叠加.滤波器的滤波效能是薄膜结构产生的谐振声场和直接通过环形空气通道狭缝声场相互作用的结果，图3详细展示了滤波器的工作原理.图3a和3b表示薄膜半径为8.5 mm、环形空气通道宽度8 mm的条件下，透射低谷频率1 194 Hz附近和峰值频率1 218 Hz附近的声波瞬态速度场.1 194 Hz处薄膜产生的声场和透过环形通道的声场之间有180°的相位差，此时在薄膜产生的声场和通过环形空气通道声场的共同作用下，以硬质铝板和薄膜结构为中心形成涡旋状的声场分布，大部分声场能量在涡旋运动中损耗而不再向前传播，从而形成透射低谷，如图3a所示.在透射最大值1 218 Hz附近，薄膜结构产生的次级声场相位与透过环形空气通道的声场相位相同，此时两部分声场步调基本相同且相互作用，致使声波透射率增强，不再产生1 194 Hz时那样的漩涡声场，如图3b所示.图3c表示在频率1 218 Hz时没有空气通道时声场的分布情况.此时在外界声场激励下薄膜达到谐振状态，振动最为强烈，薄膜和铝板圆孔中空气柱组成的整体结构的等效质量密度接近为0，薄膜等效为一个高效的声能量漏斗，产生高的声能量透过率[10].图3c是在没有环形空气通道的情况下，薄膜面积虽然仅占声硬壁面积的2.89%，但仍然能产生超常的声透射.

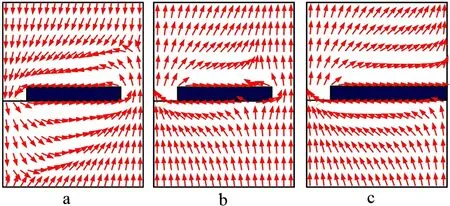
图3 不同频率和不同设置时的声场分布

滤波器的工作原理还可以通过其有效参数来进行解释.从滤波器的透射、反射数据中提取得到等效阻抗值和等效折射率，如图4所示.在低声透过率的频率为1 194 Hz时，滤波器的等效阻抗值达到最大值，表明此时的滤波器是一个具有很大声学阻尼数值的材料，等效为声波难以透过的声学硬壁，与图2所示的1 194 Hz处出现最小声透过率的结果相吻合.在图2出现透射峰的1 218 Hz处，图4显示滤波器的等效质量密度为零，说明此时声波正在透过一个没有质量的声学材料，类似于声波在自由空间中传播，与图2所示的1 218 Hz处出现最大透射率的结果也相吻合.

图4 滤波器的等效质量密度和等效阻抗值

2.3 空气流通性能与滤波能力的关系

设计具有空气流通性能的消声材料，在实际应用中需要在尽可能增大空气透过率的同时保持较低声透过率.因此，进一步讨论了环形空气通道宽度的几何尺寸对该滤波器滤波能力的影响.将环形空气通道的径向宽度分别设置为4,8,12,16,20,24和28 mm共7种尺寸，对应的滤波器的开放面积占总面积的比例分别为15.36%,29.44%,42.24%,53.76%,64%,72.96% 和80.64%.对开放面积逐渐变大情况下滤波器的声波透过率情况进行研究，仿真得到的不同开放面积滤波器的透射曲线如图5所示.从图5可以看出，随着开放面积逐渐增大，滤波器的滤波中心频率出现少许的蓝移，虽然滤波能力逐渐减弱但仍保持较强的滤波能力.按照从小到大的顺序，七种不同开放面积所对应的最低透射率分别为0.0014,0.0034,0.012,0.021,0.05,0.1和0.165.由此可见，即使开放面积占总面积的72.96%，该器件的声波透射率也没有超过0.1，表明在保证空气有效流通的情况下，滤波器仍然具有高效的噪声消除性能.在实际应用时，可以根据要求调整薄膜的谐振频率和环形空气通道的几何尺寸，构建同时满足噪声消除和空气流通性能的宽频消声材料.

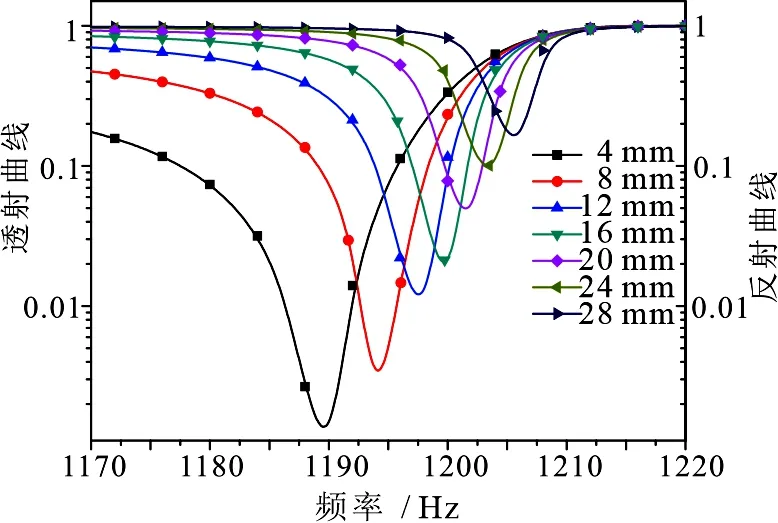
图5 不同环形空气通道缝隙宽度时的声透过率

3 结论

文中通过薄膜结构与带有空气通道的铝质声硬壁材料相结合，设计了一种具有空气流通性能的声学滤波器.通过薄膜反射声场和直接通过空气通道的声场之间的相互作用，在滤波器内部形成声涡旋而消耗声能量.滤波器允许空气流通的面积达到72.96% 和80.64%时，滤波效能分别达到90%和83.5%，较好地实现了空气流通和良好滤波效果的兼顾.通过提取等效声阻抗数值和等效折射率，进一步说明了滤波器的工作原理.在滤波效能突出的频段，滤波器等效于具有高反射率的声学硬壁，声波难以透过.通过调节薄膜和环形空气通道缝隙的几何尺寸，可以实现宽频的噪声消除，构建具有空气流通性能的消声材料.设计的滤波器消声材料在需要空气流通的噪音消除场所，例如实验室的通风设备，需要通风的工厂热交换场所，管道、机舱或轮船船舱等场所，具有广阔的应用前景.文中构建的空气流通性能声学滤波器为新型消声材料的设计提供了一种新的设计思路.