并轴式双转子永磁同步电机齿槽转矩分析

戈宝军, 姜汉, 林鹏, 陶大军

(哈尔滨理工大学 大型电机电气与传热技术国家地方联合工程研究中心,黑龙江 哈尔滨 150080)

0 引 言

在传统并行对驱设备中,经常使用一台电机驱动齿轮传动机构,从而带动设备运行。并轴式双转子永磁同步电机可替代齿轮传动机构,直接驱动双螺杆泵类等设备,由此避免了使用齿轮等机构带来的一系列问题。

与传统电励磁电机相比,永磁电机具有结构简单、体积小、运行可靠、效率高、电机形状和尺寸可以灵活多样等显著优点[1]。然而相对于电励磁电机,永磁电机会因在绕组无激励时永磁体与定子齿槽之间相互作用力的切向分量而产生齿槽转矩。并轴式双转子永磁同步电机作为一种特殊结构的永磁电机,其产生的齿槽转矩影响相对于传统永磁电机更为明显,导致电机在运行时转矩波动增大,会产生振动、噪声等不利影响。因此,分析和削弱并轴式双转子永磁同步电机的齿槽转矩对该电机设计和运行具有实际意义。

影响并轴式双转子永磁同步电机齿槽转矩有多方面的因素,定子槽口宽度、并接区气隙尺寸、永磁体结构尺寸等[2-5]。本文以一台双8极54槽表贴式并轴式双转子永磁同步电机为例,在对各前提条件进行合理假设的前提下,给出确定并轴式双转子永磁同步电机并接区气隙尺寸的一般原则,在计及并接区结构的前提下给出各部分等效磁导计算公式,并以此建立并轴式双转子永磁同步电机等效磁网络模型,求解节点磁导矩阵得到气隙磁密的解析表达式,最后采用能量差分法给出并轴式双转子永磁同步电机齿槽转矩的解析表达式,得出影响并轴式双转子永磁同步电机的主要因素。采用2D有限元分析法,结合解析计算,研究不同结构参数对并轴式双转子永磁同步电机的影响。使用田口法,以齿槽转矩为优化目标进行优化,分析对比优化前后电机各项参数,验证了田口法在并轴式双转子永磁同步电机齿槽转矩优化分析中的作用。

1 电机结构特点及运行原理

并轴式双转子永磁同步电机可等效看作由两台相同尺寸结构的永磁同步电机左右“并接”而成,如图1所示,电机定子铁心为“⊂⊃” 结构,定子铁心开槽,在定子铁心内腔中存在两个转子结构,两者并行放置,并轴式双转子永磁同步电机结构关于并接区轴线左右对称。以并接区轴线可将并轴式双转子永磁同步电机分为左侧电机和右侧电机两部分,左右两侧电机分别采用独立绕组,左侧电机绕组按照逆时针排布,右侧电机按照顺时针排布,各相绕组关于并接区轴线线对称排列,两侧绕组采用独立供电方式。为实现并轴式双转子电机的并行对驱功能,左右两侧转子上永磁体极性关于并接区中心线左右相异分布,即左侧转子永磁体“N”极对应于右侧转子“S”极,左侧转子永磁“S”极对应于右侧转子永磁体“N”极。表贴式永磁同步电机充磁方式分为径向充磁和平行充磁,对于并轴式双转子永磁同步电机两侧转子上永磁体采用径向充磁方式。

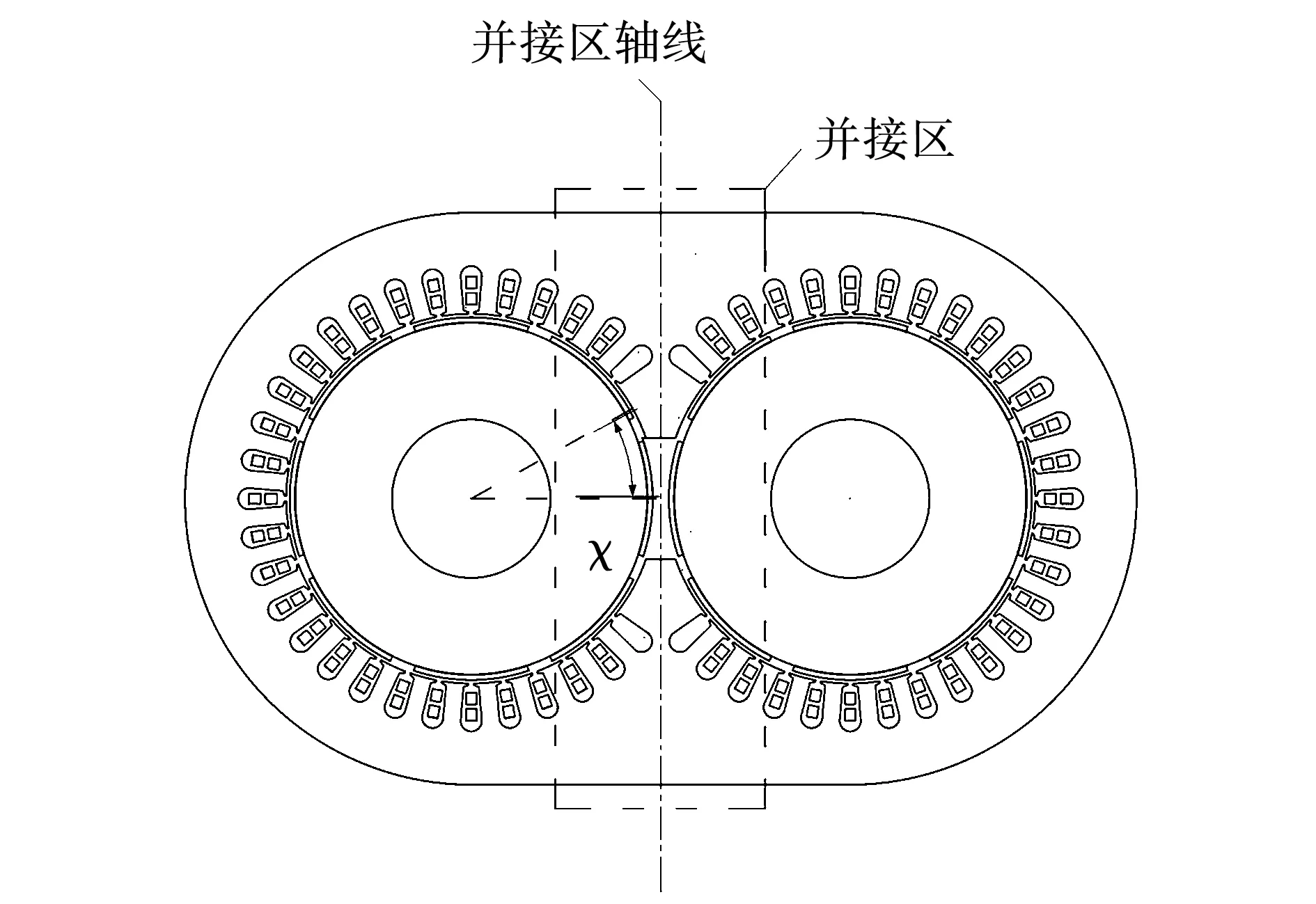
图1 并轴式双转子永磁同步电机示意图

电机运行时因为两侧电机转子永磁体极性相反,所以在电机内部两侧会形成旋转方向相反的旋转磁场,在该磁场的作用下两侧转子实现相对旋转。在中间并接区无铁心部分,两侧转子永磁体应用磁齿轮原理相互吸引,更好地保持了两侧转子旋转的同步性。

2 并接区气隙尺寸确定与等效磁路的建立

首先给出并接区气隙尺寸确定的一般原则,在此基础上对并接区进行分块并推导出并接区各部分等效磁导计算公式,进而建立并轴式双转子永磁同步电机等效磁网络模型,依据建立的等效磁网络模型列写节点磁导矩阵,最终得到各点磁动势和各支路磁通,进而得到各部分磁密。

2.1 并接区气隙尺寸的计算

本文所研究的并轴式双转子永磁同步电机,在结构上与传统电机最大的区别在于在两转子中间处出现有并接区结构,如图2所示,并接区结构的出现影响电机内部电磁场,进而影响电机的运行特性,因此确定并接区尺寸结构对于进一步分析和研究该电机具有重要意义。因其两侧电机结构对称,故选用一侧电机结构给出并接区气隙尺寸确定的一般原则。

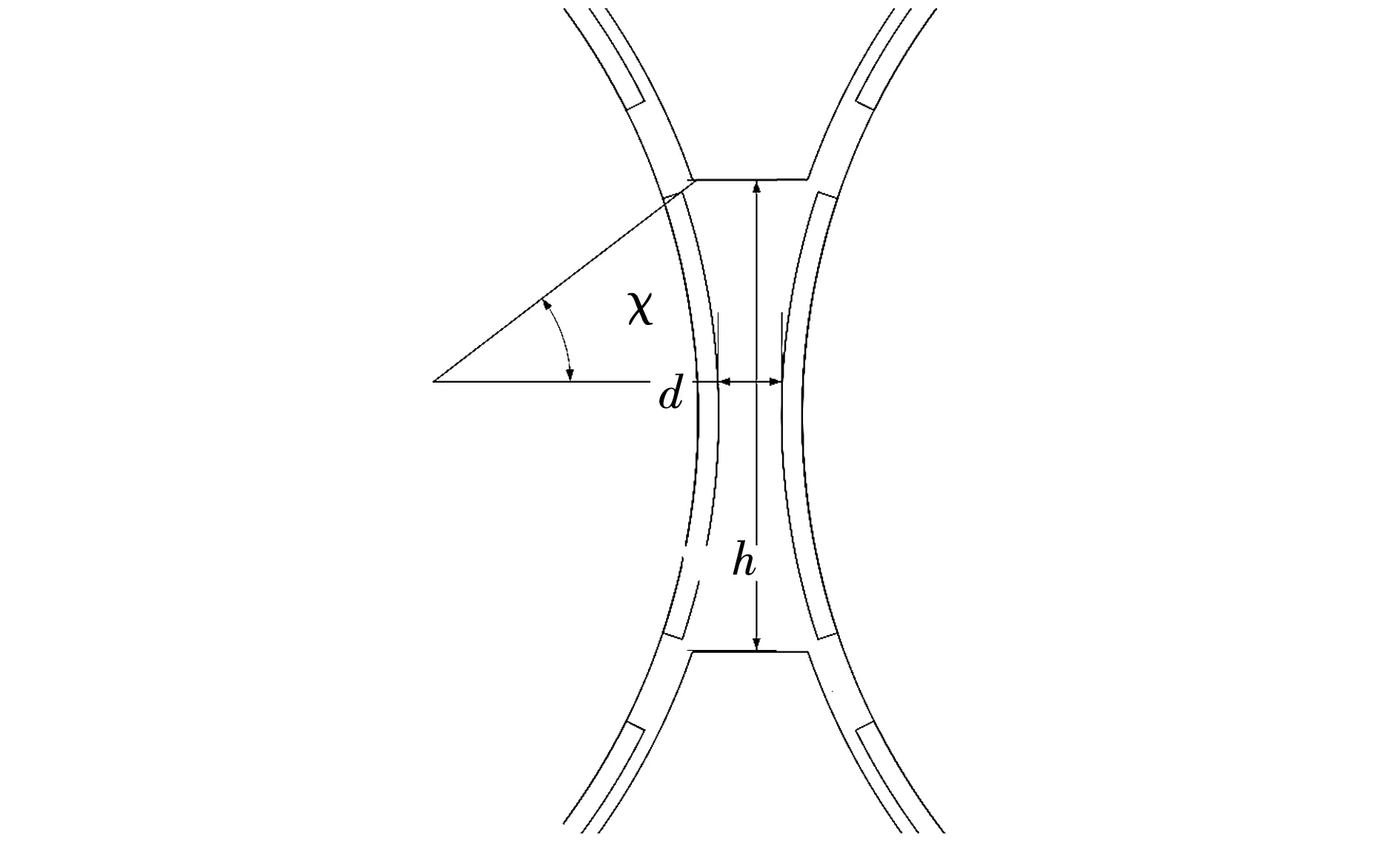
图2 并接区气隙尺寸结构确定示意图

电机每个齿宽所占圆心角为

(1)

电机每个槽宽所占圆心角为

(2)

式中:bt为定子铁心齿宽;bs0为定子铁心槽口宽度;Rsi为定子铁心内径。

并轴式双转子电机可视为由两台尺寸结构相同的永磁同步电机削去部分定子铁心后并接而成,因此单侧电机相较于常规永磁同步电机削去定子槽数为

(3)

式中:n为单侧电机相比于常规永磁同步电机削去的极数;p为电机极对数;Q为单侧电机对应的常规永磁同步电机的槽数。

并轴式双转子永磁同步电机并接区所占最大圆心角为

γmax=2π-(Q-W)α1-(Q-W-1)α2。

(4)

并轴式双转子永磁同步电机并接区所占最小圆心角为

γmin=0°。

(5)

并接区所占圆心角范围为

γmin≤χ≤γmax。

(6)

为更好地表征并轴式双转子永磁同步电机并接区结构对电机性能的影响,因此特别定义两种并接区结构参数:并接区两转子间气隙长度d、并接区两转子间气隙高度h。其具体计算公式如下:

两转子间气隙长度为

d=L-2Rsicosχ;

(7)

两转子间气隙高度为

h=2Rsisinχ。

(8)

式中L为并轴式双转子永磁同步电机两转子轴心距。

本文所研究为表贴并轴式双转子永磁同步电机,其主要参数如表1所示。

表1 电机主要参数

2.2 各部分等效气隙磁导的计算

在确定并接区尺寸结构参数后,结合电机磁路分布将电机分为多个区域,对各区域分别计算等效磁导,将各区域等效磁导连接形成磁网络。

并轴式双转子永磁同步电机等效磁网络如图3所示,磁网络模型包括:1)定子轭部磁导Λsen;2)定子齿部磁导Λstn;3)气隙磁导Λδ;4)永磁体等效磁导Λm;5)转子轭部铁心磁导Λren;6)并接区铁心轭部磁导Λde;7)并接区铁心齿磁导Λdt;8)并接区气隙磁导Λdδ;9)永磁体等效磁通源Φm。

图3 并轴式双转子永磁同步电机等效磁网络模型

根据磁导计算公式

(9)

气隙磁导可表示为

(10)

式中:μ0为空气磁导率;Sδ为气隙磁通通过的等效截面积;δ为等效气隙长度。

第n个齿的等效磁导为

(11)

第n段定子轭部的等效磁导[6]为

(12)

第n段转子轭部的等效磁导[6]为

(13)

式中:kFe为铁心叠压系数;μFe为铁心磁导率;Hstn为定子铁心齿部高度;βs为分段定子铁心轭部所对应圆心角;βr为分段转子铁心轭部对应圆心角;Rso为定子铁心外径;Rt为定子槽底外径;Rro为转子铁心外径;Rri为转子铁心内径;La为铁心长度;Lstn为铁心齿部宽度。

为方便计算并接区各部分等效磁导,将并接区进行分块,因电机结构为上下对称,故以上侧分块情况为例进行说明,如图4所示,可将并接区分为并接区定子轭、并接区定子齿、并接区气隙3部分。并接区轭部、齿部、气隙等效磁导的计算模型如图5所示。

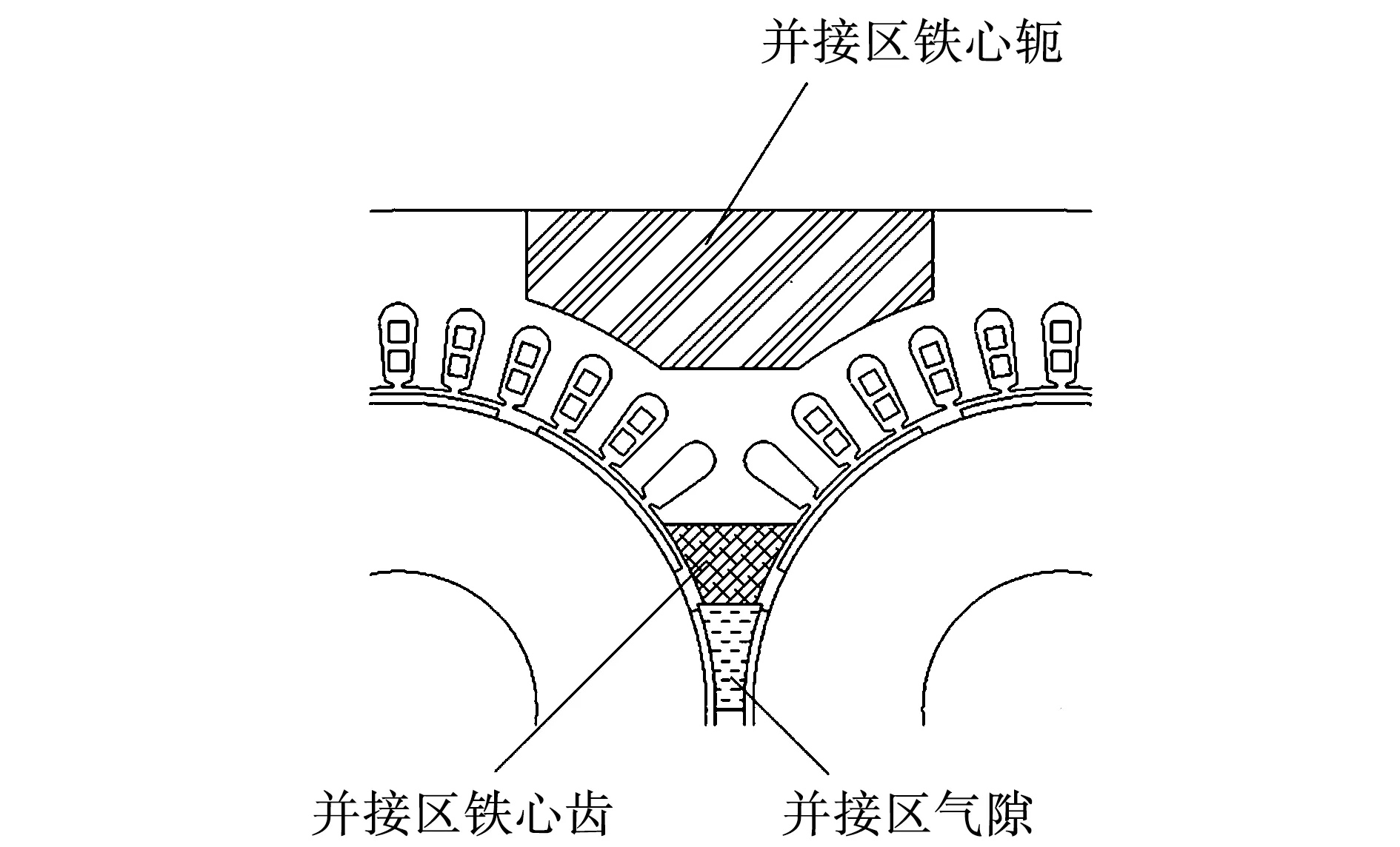
图4 并接区分块示意

图5 并接区等效磁导模型

并接区铁心齿部等效磁导为

(14)

并接区气隙等效磁导为

(15)

并接区铁心轭部可分为Ⅰ、Ⅱ两部分,如图5所示,其中Ⅰ可借鉴并接区齿部磁导计算模型,Ⅱ可借鉴电机第n段齿部等效磁导计算模型。

并接区铁心轭部等效磁导为:

Λde=ΛdeⅠ+ΛdeⅡ;

(16)

(17)

(18)

永磁体等效磁通源、永磁体等效磁导分别为:

(19)

(20)

式中:Φr为永磁体虚拟内禀磁通;Sm为永磁体提供每极磁通的截面积;H为永磁体材料磁场强度。

2.3 等效磁网络方程的建立

在确定等效磁网络参数后,等效磁网络可参照电网络列写节点磁势矩阵方程[7-8],即

[Φ]=[Λ][F]。

(21)

对式(21)进行变换可得

[F]=[Λ]-1[Φ]。

(22)

对式(22)中各矩阵进行分块可得

(23)

并轴式双转子永磁同步电机等效磁网络磁导矩阵为对称矩阵,其中G1为左侧电机内部磁导矩阵、G2为左侧电机与右侧电机间的磁导矩阵、G3为右侧电机与左侧电机间的磁导矩阵、G4为右侧电机内部磁导矩阵,其具体矩阵形式如下:

G1=

G4=

通过求解节点磁势方程可以得到各支路磁通,进而得到各部分磁感应强度为:

(24)

在计及并接区结构推导并接区各部分等效气隙磁导计算的基础上,建立并轴式双转子永磁同步电机等效磁网络模型,进而可通过求出各节点磁动势和各支路磁通得到各部分磁感应强度。

3 齿槽转矩的解析分析

在定转子相对旋转过程中,如果定转子间相对面积不发生改变,则定转子间磁场保持恒定不变。但是因为电机开槽、并接区结构的缘故,电机旋转过程中,定转子间磁导会发生改变,导致其间磁场不再恒定不变,引起磁场储能发生变化,转子上永磁体与定子齿间相互作用力的切向分量使转子回到原来的位置,因此在并轴式双转子永磁同步电机运行过程中产生齿槽转矩。

由能量差分法分析可得电机磁场储能与齿槽转矩之间的关系为

(25)

磁场能量计算公式[9]为

(26)

基于并轴式双转子永磁同步电机磁路等效模型,由磁动势和磁导关系可知,并轴式双转子永磁同步电机气隙磁通密度可表示为

Br(θ,α,χ)=Λ(θ,α,χ)Fm(θ)。

(27)

将式(27)代入式(26)可得

(28)

(29)

(30)

式中Nr、Ns分别为转子永磁体极数和定子槽数,将式(28)～式(30)代入式(25)可得电机齿槽转矩的具体表达式[10]为

(31)

通过分析齿槽转矩解析表达式可知,并轴式双转子永磁同步电机齿槽转矩与并接区尺寸结构、永磁体结构、定子齿槽结构等因素有关,以下将通过有限元仿真计算分析各因素对电机齿槽转矩的影响规律。

4 齿槽转矩有限元分析

分别就并轴式双转子永磁同步电机定子槽口宽度、并接区气隙尺寸、永磁体结构尺寸及定子斜槽对齿槽转矩的影响进行有限元仿真计算,并对计算结果进行分析。

4.1 定子槽口宽度对齿槽转矩的影响

针对不同槽口宽度对电机齿槽转矩的影响进行有限元仿真计算,仿真结果如图6所示。两侧转子齿槽转矩变化趋势具有一致性,可以看出随着定子槽口宽度的增加,齿槽转矩也随之增加,齿槽转矩随槽口宽度的变化呈正相关,定子槽口宽度由1 mm增加到3 mm,齿槽转矩变化了3.78 N·m。电机设计过程中,在符合加工工艺的要求下,尽可能选择合适的槽口宽度或使用磁性槽楔以减小齿槽转矩。

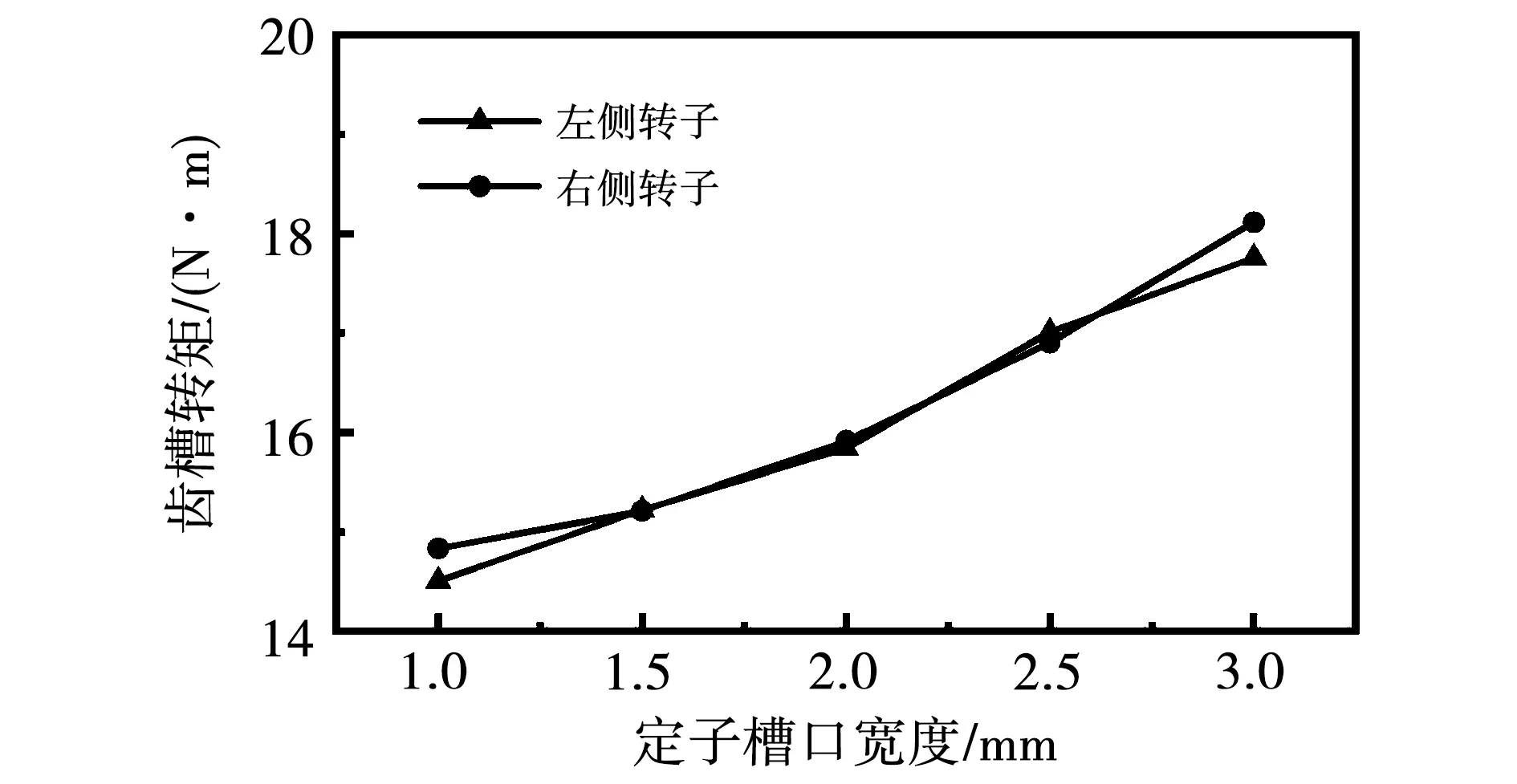
图6 齿槽转矩随定子槽口宽度变化趋势

4.2 并接区尺寸结构对齿槽转矩影响

通过分析可知,并接区结构作为并轴式双转子永磁同步电机的特殊结构,它的存在对于电机的运行性能有非常重要的影响。为此,分别计算两转子间不同气隙长度、高度以及两者同时变化时对电机齿槽转矩的影响,计算结果如图7～图9所示。

图7 齿槽转矩随两转子间气隙长度的变化趋势

如图7所示,当h<4 mm时,齿槽转矩随着两转子间气隙长度的增加而减小;当h>4 mm时,齿槽转矩随着两转子间气隙增加而增加;在h=4 mm时,齿槽转矩有最小值。

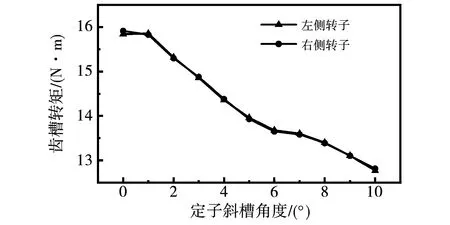
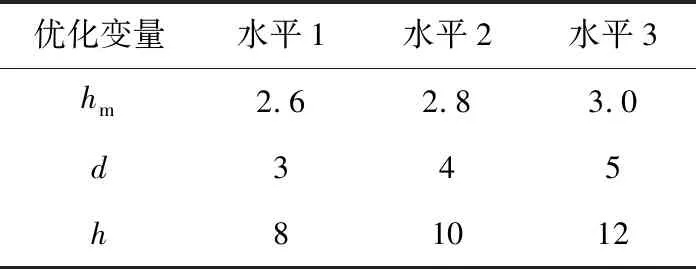
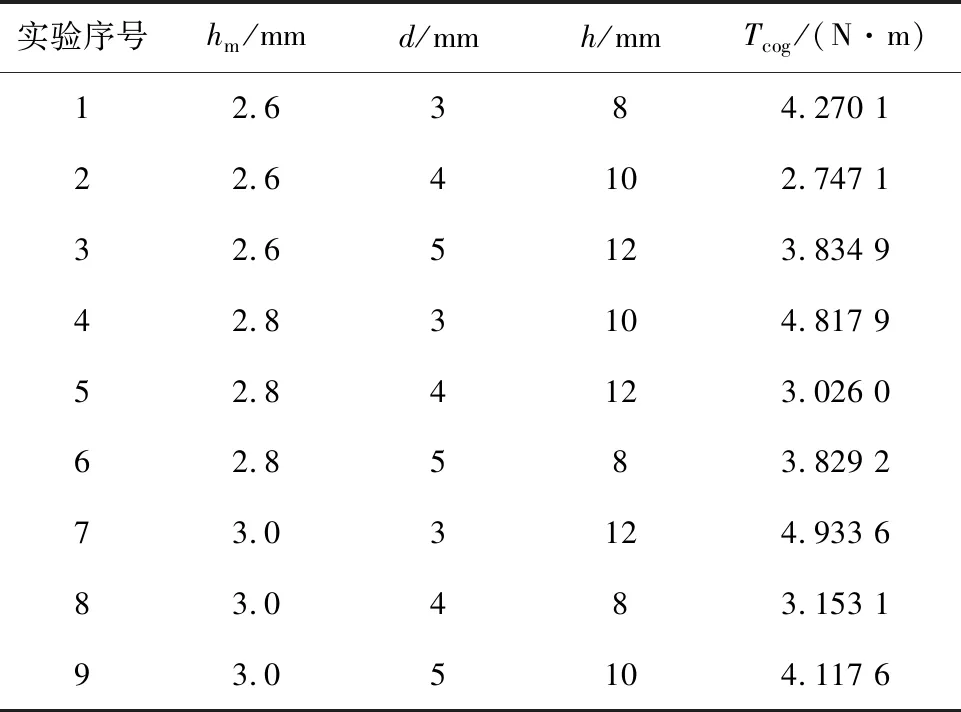
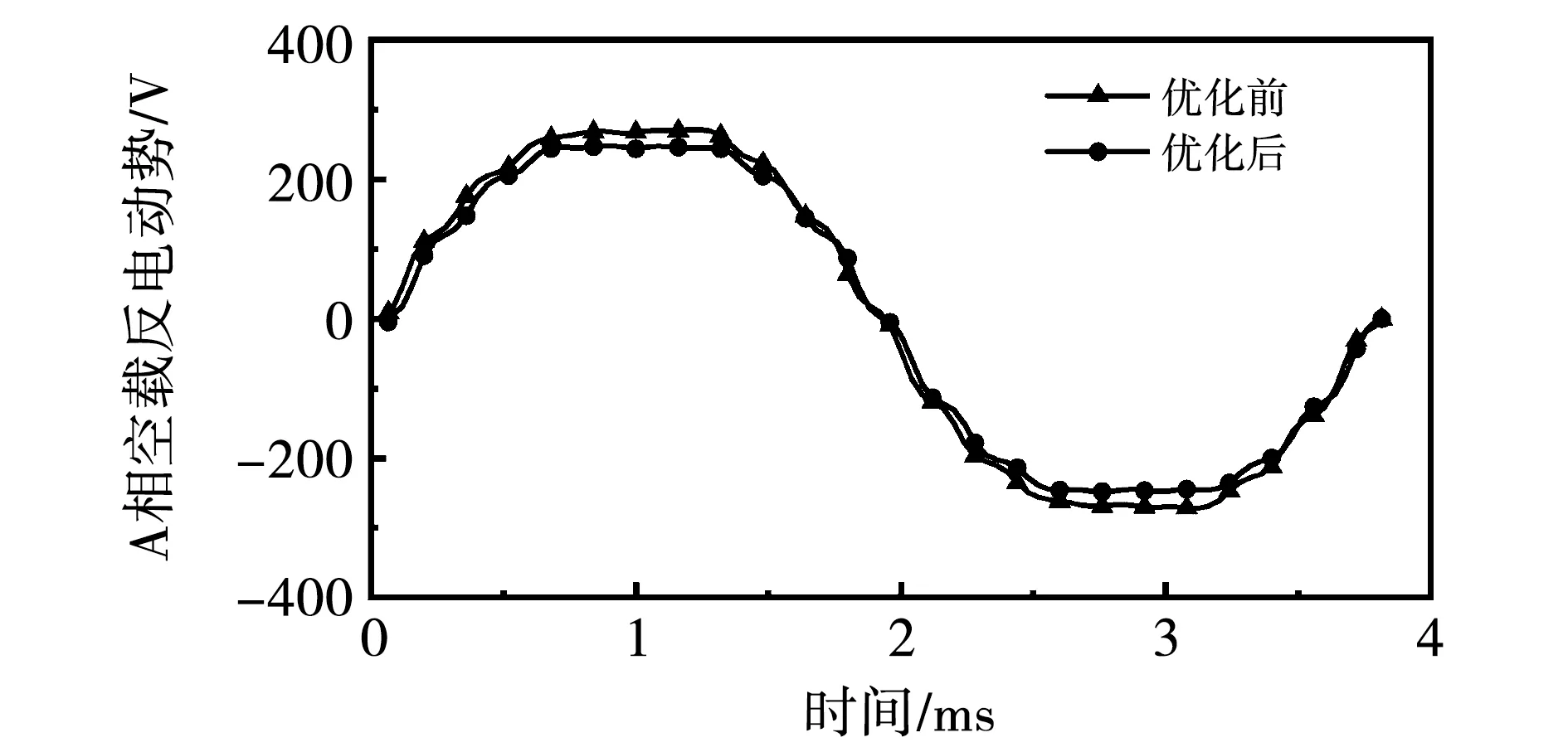
如图8所示,齿槽转矩随两转子间气隙高度增加而增大,在10 mm≤h≤50 mm,齿槽转矩近似线性变化,变化值为7.1 N·m;50 mm

图8 齿槽转矩随两转子间气隙高度的变化趋势

如图7和图8所示,为仅考虑单一变量作用时齿槽转矩的变化情况,为更全面地反应并接区气隙尺寸对电机齿槽转矩的影响,需考虑到并接区气隙长度、高度同时变化时齿槽转矩的变化规律。计及并接区两转子间气隙长度、高度同时变化时齿槽转矩的变化情况,仿真计算结果如图9所示。对图9可作如下分析:

图9 齿槽转矩随两转子间气隙长度、高度变化趋势

1)将两转子间气隙高度h作为研究变量,两转子间气隙长度在不同范围内变化。当d<6 mm时,齿槽转矩与两转子间气隙高度呈现正相关,最大值为15.7 N·m、最小值为3.72 N·m,变化差值为11.98 N·m,其变化趋势如图9中曲线3所示;当d≥6 mm,齿槽转矩随转子间气隙高度的增加而增大,但在不同的h范围内增大程度不同,在10 mm≤h<40 mm范围内变化值约为9.2 N·m,在40 mm≤h≤70 mm范围内变化值约为0.43 N·m,其变化曲线如图9中曲线2所示。

2)将两转子间气隙长度d作为研究变量,两转子间气隙高度在不同范围内变化。如图9中曲线4、曲线5、曲线6所示,齿槽转矩在该转子间气隙长度变化范围内齿槽转矩总体呈现增大的趋势。当10 mm≤h<40 mm,齿槽转矩变化值为11.98 N·m,其变化趋势如图9中曲线6所示;当40 mm≤h≤70 mm,齿槽转矩变化值约为11.58 N·m,其变化趋势如图9中曲线5所示。

计及并接区转子间气隙长度、高度同时变化的作用,齿槽转矩变化值约为15.43 N·m。两转子间气隙长度、高度的不同组合情况,对齿槽转矩变化影响较大。

4.3 永磁体尺寸结构对电机齿槽转矩的影响

由齿槽转矩解析计算分析可知,齿槽转矩受电机气隙磁场影响,而空载情况下,电机内的气隙磁场主要由永磁体产生,永磁体的变化影响气隙磁场,进而影响电机的齿槽转矩。研究电机齿槽转矩的变化,应当考虑永磁体尺寸结构对其影响。

通过仿真计算分别得出齿槽转矩随永磁体厚度、永磁体极弧系数的变化趋势,如图10～图11所示。从图10可以看出,随着永磁体厚度增加齿槽转矩呈现不断增大的趋势。当永磁体厚度为2.5 mm时,齿槽转矩出现最小值,左侧转子为13.1 N·m、右侧转子为13.1 N·m,永磁体增加1.5 mm,齿槽转矩变化8.2 N·m。

图10 齿槽转矩随永磁体厚度变化趋势

图11 齿槽转矩随永磁体极弧系数变化趋势

从图11可以发现,齿槽转矩受永磁体极弧系数影响较大。当αp=0.6时,齿槽转矩有最小值,左侧转子为13 N·m、右侧转子为12.5 N·m;当αp=0.72时,齿槽转矩有最大值,左侧转子为16.8 N·m、右侧转子为16.5 N·m,齿槽转矩随永磁体极弧系数αp(0.6≤αp≤0.8)变化幅度约为4 N·m。

4.4 定子斜槽对齿槽转矩的影响

并轴式双转子永磁同步电机使用斜槽结构,同一时刻永磁体在定子齿槽轴向各处所产生的切向力各异,因此在一定斜槽角度内可以有效削减齿槽转矩。并轴式双转子永磁同步电机共计54槽,单侧电机所占27槽,所占角度为270°,当定子槽与电机转子轴线所夹角度为10°,即斜过一个定子齿距。

齿槽转矩随定子斜槽角度变化趋势如图12所示,斜槽角度为0°时,其齿槽转矩为15.9 N·m,在定子斜槽10°范围内,随着斜槽角度的增加齿槽转矩有所减小,最小齿槽转矩为12.8 N·m。斜槽角度在0°～10°范围内变化,齿槽转矩减小3.1 N·m,通过分析可知在合适的斜槽角度变化范围内,定子斜槽对齿槽转矩具有削弱作用。

图12 齿槽转矩随定子斜槽角度变化趋势

5 基于田口法的齿槽转矩优化及电机性能分析

5.1 齿槽转矩优化

通过上述分析可知,永磁体厚度及极弧系数、并接区两转子间气隙长度和高度对电机齿槽转矩有较大的影响,为此选取永磁体厚度hm、两转子间气隙高度h、两转子间气隙长度d作为关键因子,关键因子取值如表2所示。各关键因子建立正交实验表,如表3所示。通过前述分析可知,并轴式双转子永磁同步电机左侧和右侧转子齿槽转矩变化具有一致性,故在此仅对左侧转子齿槽转矩进行优化。

表2 关键因子取值

表3 实验正交表及计算结果

齿槽转矩平均值计算[11]为

(32)

式中:Tm为某一优化变量的平均值;Tcogi为第i次优化目标值,通过上式计算可得Tm=3.858 8。计算各关键因子在每一水平下的齿槽转矩如表4所示,各关键因子对齿槽转矩影响所占比重如表5所示。

表4 各性能指标平均值

表5 各关键因子对齿槽转矩影响所占比重

关键因子对齿槽转矩所占比重计算[11]为

(33)

式中:SSx为x关键因子对齿槽转矩所占比重;Tm,x,i为x关键因子i水平的平均值;Tm为9组实验齿槽转矩的平均值。

从表5中可以看出,并接区两转子间气隙长度d对电机齿槽转矩的变化有重要影响,所占比重为92.28%。并且通过上述优化分析可得,在hm=2.6 mm、d=4 mm、h=10 mm时,电机齿槽转矩有最小值为2.747 1 N·m,相比优化前齿槽转矩下降了13.09 N·m。

5.2 电机性能仿真分析

利用田口法对电机参数进行优化,根据上述优化确定的参数,对电机进行有限元仿真对比分析优化前后电机的性能。

图13为优化前后电机并接侧空载气隙磁密对比,从图中可以看出优化前并接侧空载气隙磁密所含谐波较多,磁密波形畸变严重,通过对该波形进行谐波分析可得,其基波幅值为0.72 T,所含谐波主要为2、3、7次,其波形畸变率为29.4%;优化后,气隙磁密波形为平顶波,其基波幅值为0.78 T,所含谐波主要为3、7次,且谐波幅值相对较低,波形畸变率为21.5%。

图13 并接侧空载气隙磁密波形

考虑到转子旋转运动中并接区两侧转子永磁体相对位置的变化对并接侧气隙磁密的影响,因此给出不同时刻下各空载气隙磁密的谐波分析结果,如图14所示,可以明显看出随着两侧转子旋转运动,空载气隙磁密谐波次数及含量各不相同。

图14 并接侧空载气隙磁密谐波分析

图15为优化前后不同时刻下空载气隙磁密幅值及波形畸变率,可以明显看出优化后空载气隙磁密基波幅值略有增加,波形畸变率显著降低,且优化后波形畸变率基本趋于稳定。

图15 空载气隙磁密基波幅值及波形畸变率

电机空载反电势为电机评估电机性能的重要参数,理想情况空载反电动势应为正弦波,但因绕组分布或永磁体分布的影响,使得空载反电势中因出现谐波而导致空载电动势波形畸变。

图16为A相空载反电动势波形,可以看出优化后空载反电势较优化前略有下降,但优化后空载反电势波形具有更好的正弦度。

图16 A相空载反电势波形

图17(a)、图17(b)分别为优化前和优化后三相空载反电动势谐波分析结果。

图17 空载反电动势谐波分析

如图17(a)所示,优化前A相、B相、C相空载反电动势基波幅值分别为296.4、301、306 V,幅值略有差别,且各相谐波次数及含量各有不同,三相电势存在有不对称性。如图17(b)所示,优化后A相、B相、C相空载反电动势基波幅值分别为274.3、274.2、274.2 V,各相谐波次数及含量基本一致,三相电势具有较好的对称性。

图18为优化前后电机左侧转子齿槽转矩,不难看出优化前电机齿槽转矩为15.8 N·m,优化后齿槽转矩为2.7 N·m,经过优化电机齿槽转矩下降13.1 N·m,优化效果明显。

图18 优化前后齿槽转矩对比

图19为优化前后左侧转子电磁转矩对比情况。优化前电磁转矩最大值为69.5 N·m,最小值为41.6 N·m,转矩脉动百分数为50.2%;优化后电磁转矩最大值为56.2 N·m,最小值为50.6 N·m,转矩脉动百分比为10.5%。通过使用田口法对并轴式双转子永磁同步电机齿槽转矩优化,对电机输出的转矩脉动有明显的削弱效果,优化后相比于优化前转矩脉动下降79%,转矩脉动下降明显。

图19 优化前后电磁转矩对比

6 结 论

基于并轴式双转子永磁同步电机并接区尺寸确定的一般原则,建立电机等效磁网络,进而推导出并轴式双转子永磁同步电机齿槽转矩的解析表达式,结合有限元计算仿真得出了槽口宽度、并接区结构尺寸、永磁体厚度、永磁体极弧系数以及定子斜槽角度对齿槽转矩的影响。在上述分析的基础上,使用田口法对电机齿槽转矩进行优化设计,最终对电机优化前后的性能参数进行分析对比,验证了田口法对并轴式双转子永磁同步电机齿槽转矩优化的实用性。通过本文分析研究可得如下规律:

1)齿槽转矩为永磁体与定子齿槽间相互作用力的切向分量引起,因此选择合适的槽口宽度、永磁体尺寸可以有效减少并轴式双转子永磁同步电机的齿槽转矩;

2)并接区结构是并轴式双转子永磁同步电机具有的特殊结构,并接区两转子间气隙长度和高度的不同组合情况对电机齿槽转矩影响较大,在电机设计过程中应当考虑并接区尺寸结构对并轴式双转子永磁同步电机齿槽转矩的影响;

3)对并轴式双转子永磁同步电机使用田口法进行优化后,电机齿槽转矩明显下降,且电机性能得到改善,验证了田口法在并轴式双转子永磁同步电机齿槽转矩优化中的作用。