Massive MIMO 中通信高效的分布式预编码设计

李勉，李洋，张纵辉，史清江

（1.香港中文大学（深圳）理工学院，广东 深圳 518172；2.深圳市大数据研究院，广东 深圳 518172；3.鹏城国家实验室，广东 深圳 518055；4.琶洲实验室（黄埔），广东 广州 510555；5.同济大学软件学院，上海 200092）

0 引言

大规模多输入多输出（Massive MIMO）是5G及未来无线通信系统中的核心技术[1-2]，其核心思想是给基站配置几十乃至数百根天线，同时为几十个用户提供高质量的通信服务。大量天线的加持极大地提高了基带处理的空间分辨率，从而有效提升了通信系统的频谱效率[3]。此外，Massive MIMO 可以利用终端移动的随机性、信道衰落的不相关性、不同用户间信道的近似正交性降低用户间干扰和误码率，实现多用户空分复用。基于以上特点，近年来，Massive MIMO 在LTE 演进、5G 和6G 领域被广泛讨论[4]。

Massive MIMO 也给无线系统的实现带来了巨大的挑战。一方面，天线数量的增加大幅提高了基带处理任务的复杂度，这对芯片的处理性能提出了极高的要求；另一方面，Massive MIMO 系统需要支持大量天线，因此需要在芯片设计中综合考虑天线数量、布局、尺寸等复杂因素。这两方面因素导致单基带处理单元（BBU）芯片系统在成本和技术难度上缺乏优势，因此无线设施供应商都转向了多BBU 芯片基站系统的方案。

多BBU 系统支持灵活可扩展的部署，根据基站天线数量要求调整芯片数量。将基带处理任务分配到多块芯片上进行，降低了对芯片处理性能的要求，是一种可行且经济的设计。主流的基于多BBU系统的天线阵列可以把天线数量做到192 甚至更多，但是在进一步增加天线数量时会遇到数据交互，也就是前传流量带宽的瓶颈。具体而言，当多个BBU 芯片联合进行基带处理时，芯片间的数据交互量随着天线数量的增加而增长，最终变得难以承载。例如，考虑一个配备256 根天线、12 bit 模数转换器（ADC,analog to digital converter）的基站，当带宽为80 MHz 时，基站BBU 的前传速率需求将达到1 Tbit/s，而这样的高数据速率已经超出了现有数据互联标准的承受能力[5-7]。

分布式基带处理系统的BBU 间过高的前传流量是阻碍更大规模天线阵列发展的重要因素，是工业界在攻克512 天线乃至1 024 天线Massive MIMO系统的过程中必须解决的问题。除了研究更高数据交换速度的总线互联接口，另一个值得重点研究的问题是如何从算法层面降低多BBU 系统的前传流量。工业界的多BBU 系统通常基于“中心节点-分布式节点”的系统架构，其特点是分布式节点处理局部天线数据，中心节点融合处理全局天线数据，达到和集中式算法等效的结果，通用的优化前传流量的手段主要还是直接的数据压缩，如离散傅里叶变换（DFT）去噪、量化压缩[8]等。

如何在保证性能的前提下优化分布式预编码算法的性能是本文考虑的核心问题。学术界关于分布式预编码算法已经有一部分工作。最早的相关工作来自文献[9-10]。文献[9-10]首次提出了下行的分布式基带处理架构，并在该架构上设计了基于交替方向乘子法（ADMM,alternating direction method of multiplier）的迫零（ZF,zero forcing）[11]预编码算法。后来学术界又提出了基于坐标下降（CD,coordinate descent）[5]、维纳滤波（WF,Wiener filter）[12]、消息传递（MP,message passing）的近似ZF 和最大比传输（MRT,maximal ratio transmission）的方法[13]。以上工作假定节点之间的连接速率十分受限，因此和工业界的应用仍存在一定割裂的现象，并且由于MRC 和ZF 预编码的性能不佳，应用潜力不大。在线性预编码算法领域，WMMSE（weighted minimum mean squared error）[14]在至今十多年来一直被视为性能上界的标准。尽管其计算复杂度很高，但是随着移动互联网对预编码算法性能要求的不断提升，WMMSE 也逐渐被部署到现网中。目前，学术界还没有关于WMMSE 的分布式预编码算法的工作，而前述分布式预编码工作以ZF 预编码作为近似性能的上界，同场景下参考价值较低。因此在评估本文算法的性能时，将以集中式ZF、集中式WMMSE 算法作为对比算法。

本文提出了一种通信高效的分布式预编码方案，其核心思想为分布式算法框架与可学习数据压缩模块的有机结合。该方案的基础是一种基于WMMSE 预编码的分布式变体，被称为分布式R-WMMSE[15]算法。通过向该算法框架中引入可学习模块并进行联合优化，保证了预编码的性能并实现了前传交互的优化。所提方案对可学习压缩模块采用极简的设计，实现了预编码性能和前传交互之间的良好折中。仿真表明，相对于经典的WMMSE算法，本文所提算法在保证预编码性能的前提下，大大降低了前传流量带宽。

1 系统模型

1.1 预编码问题

基站端根据下行信道信息求解不同用户的预编码矩阵。数学上，以最大化加权和速率（WSRM,weighted sum rate maximization）为目标，该问题可以表示为

其中，αk≥ 0表示用户k的权重，Pmax表示基站的最大发射总功率。事实上，式(2)中目标函数是频谱效率的加权之和，其与带宽的积才是加权和速率。带宽在该优化问题中是常量，因此将频谱效率和可达速率作为目标函数是等效的，故本文也沿用相关工作[14,16]对该问题的称呼。

用户k的信干噪比（SINR,signal-to-interferenceand-noise ratio）为

Massive MIMO 的一个重要优势是当基站天线数M大于用户天线数N时，随着M的增加，线性预编码的频谱效率可以逐渐接近理想的频谱效率[17]。反之，当M≈N时，信道线性自相关程度会增加，导致频谱效率降低。

在实际应用中，正常情况下基站工作于M＞N的状态。为了实现单用户频谱效率和能耗之间的良好折中，通常采用用户调度和天线关断等手段，以维持比值在一个适当的范围内。本文的讨论也仅考虑M＞N的情形。

1.2 分布式预编码

多BBU 系统采用星形拓扑架构执行分布式预编码。具体而言，系统将基站天线分成不同的簇，每簇天线对应一个局部的BBU，使每个BBU只负责局部信号的处理。同时，一个中央BBU节点处理对应的全局数据。这种多BBU 系统能够适应更加灵活的天线数量和分布式的部署，相对于单BBU 系统，它能够降低对处理芯片性能的要求。

本文考虑如图1 所示的分布式基带处理星形架构，其由一个中心节点和C个局部节点（对应C簇天线的BBU）组成。这种架构广为采用，其原因是它能够很好地适应天线分簇所产生的处理流程。天线分簇自然会产生“局部数据”和对应的局部节点；高性能算法需要综合全局数据进行运算，这对应于中心节点的数据处理；而数据汇总和分发的过程则需要中心节点和局部节点之间的数据通路。

图1 分布式基带处理星形架构

分布式预编码的前传数据交互是一个往返的过程。局部节点首先对局部信道矩阵Hc进行预处理和压缩，然后将压缩结果汇总到中心节点进行进一步运算；中心节点在运算完毕后，将运算结果压缩并传回各个局部节点，然后由各个局部节点计算得到其各自的预编码矩阵。

2 通信高效的分布式预编码设计

本节主要介绍所提方案的技术细节。首先简要介绍了WMMSE 预编码算法，接着介绍了该算法的一种变体，即R-WMMSE 分布式预编码，并将其作为本文方案所使用的优化算法框架。在学习方法部分，分别详述了可学习数据压缩模块的设计思路与分析，以及模块与算法框架的整合和联合优化的细节。分布式预编码算法框架与可学习的数据压缩模块共同构成了一个完整的分布式预编码方案。

2.1 WMMSE 预编码算法简介

WMMSE[14]是一种高性能MIMO 线性预编码算法。其核心在于将原始的最大化加权和速率问题式(2)等价转化为

其中，Wk为新引入的辅助变量，Ek为用户端均方误差矩阵，定义为

其中，Uk为用户端接收合并矩阵。

通过对问题式(5)采用块坐标下降（BCD,block coordinate descent）法，可以得到经典的WMMSE算法。每次迭代依次更新Uk、Wk、Pk

对Pk的子问题求解涉及能量约束，因此需要优化对偶变量μk。预编码矩阵的能量是关于μk的单调函数，所以在优化μk时需要使用二分法[14]。WMMSE 预编码算法如算法1 所示。

算法1WMMSE 预编码算法

2.2 R-WMMSE 分布式预编码算法

本文的分布式预编码方案使用一种WMMSE算法的分布式变体（称为R-WMMSE）作为算法框架，可提供较好的可解释性。利用优化问题中最优解的子空间特性，R-WMMSE 分布式预编码将BBU间的交互数据压缩到相应的低维子空间，从而有效地降低了数据交互量。需要强调的是，在预编码性能上，R-WMMSE 预编码和WMMSE 预编码具备相同的性能。

在对R-WMMSE 分布式预编码算法进行推导前，先介绍引理1。

下面证明新构造的可行解具有更优的性能（目标函数值）。这样的结论基于式(12)的正定性

基于引理1，可以证明定理1[15]。

R-WMMSE 分布式预编码算法执行流程如算法2 所示。

算法2R-WMMSE 分布式预编码算法

评估算法在实际系统中的性能表现时，需要综合考虑全频带、用户调度、算法时间分配等因素，因此本文只能给出简易的估算。下面给出一个示例，当考虑M=128、N=D=16、C=4 时，WMMSE预编码的数据交互量为 4 096 个复数，而R-WMMSE 的数据交互量仅为1 536 个复数。当全频带为80 MHz 时，按照30 kHz 一个子载波进行切分，复数量化位数为12 bi（t6 bit 实部和6 bit 虚部），算法执行时限定时间分配为0.3 ms，那么WMMSE预编码执行过程的数据交互为 488.28 Gbit/s，R-WMMSE 预编码则为183.11 Gbit/s。如果该基站系统最高支持 500 Gbit/s 前传带宽，那么使用WMMSE 预编码时，系统只能驱动上面介绍的128天线，而使用R-WMMSE 预编码时则能够驱动256天线（M=256,C=8）。

以上分析表明，在常规的基站规模配置下，相较于WMMSE 算法，R-WMMSE 分布式预编码大幅优化了前传交互量。同时，示例直观展示了优化数据交互量如何帮助系统支持更大规模的天线阵列。

2.3 可学习的数据压缩模块设计

为了进一步降低算法2 中（第1 行和第8 行）的数据交互量，本节给出可学习的数据压缩模块设计。所介绍的模块设计不依赖于特定预编码算法，而是能与本文提到的各种方法（如ZF 预编码、WMMSE 预编码、R-WMMSE 预编码等）结合。本文以R-WMMSE 分布式预编码为例展示方案的可行性。

下面分别介绍3种不同的可学习的数据压缩模块。

1) 单边压缩（SSC,single sided compression）模块

考虑一种简单的矩阵单边压缩，即

其中，θ1即P1，θ2包含P2和S两部分，总参数量为mn+2mp。由的表达式可以看到，SSC 压缩方式要求q=n,p＜m。

2) 双边压缩（DSC,double sided compression）模块

另一种压缩模块执行对矩阵的双边压缩，即

3) 全连接（FC,fully connected）模块

参考神经网络的全连接设计，可以直接得到如下的全连接数据压缩模块设计

其中，reshape 函数和vec 函数正好是一对互逆的映射，reshape 的第二个参数表示输出矩阵的维度，θ1即P3，θ2包含P4和S两部分，总参数量为mn+2mnpq。

下面分析以上3 种模块的输出元素关于输入元素的依赖关系。所提出的2 种模块中SSC 的输入输出关系根据式(20)可以表示为FSSC(A)=P2P1A+S。记=P2P1，可以得到如下的逐元素输入输出关系

对比式(23)～式(25)，有以下发现。

①SSC 模块的第k行第l列输出元素为A中第l列元素的线性组合再加上一个常数。

②DSC 模块的第k行第j列输出元素为A中所有元素的线性组合再加上一个常数，因此具备比SSC 更强的输入输出关系表达能力。

③FC 模块的第k行第j列输出元素为A中所有元素的线性组合再加上一个常数，且线性组合权重不共享，和DSC 具有同水平的输入输出关系表达能力。

值得注意的是，压缩解压层次更多的单边矩阵压缩、双边矩阵压缩模块可以化简为SSC 和DSC 模块。例如，包含多个压缩解压矩阵的双边压缩模块

综合比较上述3 种可学习压缩模块的参数量和表达能力，当m,n,p,q的数量级相同时，有以下结论成立。

①复杂度方面：FC 相比SSC 或DSC 模块的参数量高2 阶，对应地引入了高2 阶的计算复杂度。

②表达能力方面：FC 和DSC 模块的表达能力水平相同，且都高于SSC 模块。

本文认为，所提出的SSC 和DSC 模块相比FC模块在复杂度和性能方面都分别实现了更好的均衡，后文将用实验佐证该观点。此外，值得注意的是，以上模块设计所引入的计算复杂度和参数存储开销的量级都不大。其中，计算复杂度和原矩阵所做的矩阵乘法相当，而参数存储开销同样和原矩阵的维度相当。

2.4 分布式算法和可学习压缩模块的联合优化

本节介绍可学习数据压缩模块和分布式算法框架进行联合优化的模型训练方法，并阐述可学习模块提升模型性能的机理。

最直接的模型优化方式是有监督学习，其直接优化SSC、DSC 的输入输出间的差距，如优化输入输出的均方误差（MSE,mean square error）

其中，期望E 是通过对大量随机生成的样本A取平均近似得到的。采用梯度下降（GD,gradient descent）法优化式(27)得到可学习压缩模块的参数后，即可将其植入R-WMMSE 分布式算法中。尽管基于式(27)的独立优化简单且直接，但是其最终得到的模型预编码性能会有较大的损失。其根本原因在于，训练后的带压缩预编码仅逼近未压缩预编码，并没有考虑到对和速率的优化。例如，本文基于2 轮迭代的R-WMMSE 的带压缩预编码，其性能上限是2 轮迭代的R-WMMSE 预编码，此时其性能与R-WMMSE 预编码的收敛性能还有较大差距。

为了避免上述的性能损失，本文提出使用无监督学习的方案。直接以下行加权和速率为目标函数（见原问题式(2)），对可学习压缩模块和分布式预编码采用端到端的联合优化。如算法3 所示，算法执行主要分为3 个阶段。第一阶段为信道数据的预处理及汇总（第1～2 行）；第二阶段为预编码的中心迭代计算（第3～7 行）；第三阶段为预编码矩阵的分发和局部计算（第8～9 行）。为了优化可学习压缩模块中的参数值，本文对算法3 采用基于反向传播的梯度下降法。具体而言，首先产生一个训练集Ω={H(1),H(2),…,H(S)}，其中，S表示训练集的样本数。对于每个样本，执行算法3 输出P(H(i))，其中，i表示第i个样本，然后以和速率为目标函数通过反向传播计算其关于压缩模块参数的梯度，从而采用GD 法更新参数值。

算法3通信高效的分布式预编码算法

值得注意的是，当固定迭代次数时，在特定压缩维度下，本文提出的基于无监督联合优化的算法3 的性能可以超越同迭代次数（如2 轮，此时优化迭代算法未收敛）的无压缩损失的R-WMMSE 算法2。这是因为无监督优化的算法3的训练目标为达到最优解，而固定迭代次数的算法2 在相应迭代次数下尚未收敛，性能比全局最优解更差。因此算法3 通过训练有机会得到比算法2 性能更好的解。

为了直观理解，可以考虑一种特殊情况，即压缩模块不执行维度压缩（输入、输出和压缩维度都相等）。通过恰当的初始化，可将学习模块变成一个恒等映射，从而在相同迭代次数下，算法3 模型的初始性能和算法2 相等。训练开始时，算法3 模型性能并非最优，可学习压缩模块的参数梯度不为0。因此，通过GD 法更新参数，可学习模块的映射输出逐渐改变，从而在恒等映射的基础上产生一个有助于提升目标函数值的偏置（例如，使解更接近最优解）。利用多个迭代中的可学习压缩模块，算法3 模型可以累积多次性能提升，比同迭代次数的算法2 性能更佳。

3 实验结果与分析

本节通过仿真实验，展示所提出的通信高效的分布式预编码算法3 相比于传统算法在预编码性能和前传通信效率方面的优势，证明本文方案对于降低前传流量、支持更大天线阵列的意义。

仿真设置如下，基站天线数M=64，分为C=8簇，用户数K=8，每个用户的天线数Nk=4，数据流数Dk=2，则总天线数N=32，总流数D=16。采用 QuaDRiGa（quasi deterministic radio channel generator）信道生成套件（版本v2.2.0）[18]按照3GPP-mmw 标准建模[19]生成信道数据。训练集包含12 000 个信道矩阵，测试集包含1 200 个信道矩阵。仿真信道参数设定如表1 所示。

表1 仿真信道参数设定

在算法3 的训练中，样本的SNR 在-10～25 dB均匀随机产生。训练和预测中，算法3 的迭代次数固定为T=2。将算法3 与现有方法WMMSE 预编码进行对比，其中，WMMSE 和R-WMMSE 的迭代次数都为6 次，与完全收敛的性能之间还存在一定差距，这部分性能区间用于展示算法3 对性能的优化。

图2(a)和图2(b)分别展示了将X∈C32×16的维度压缩为16×16 和12×16 时在DSC、SSC、FC 这3 种数据压缩模块下算法3 的性能。图2(a)将X压缩到了其秩的维度，而图2(b)则将X压缩到了比其秩更小的维度。实验中WMMSE 与R-WMMSE 的性能几乎一致，代表了使用“无损压缩”的现有方法的性能。

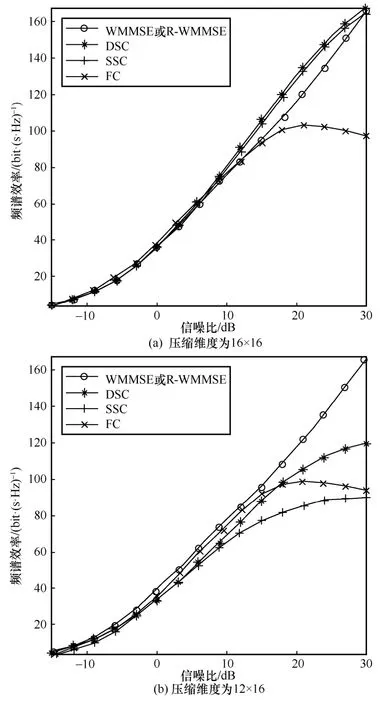
图2 压缩维度为16×16 和12×16 时在3 种数据压缩模块下算法3 的性能

从图2(a)可以看到，当X被压缩到其秩的维度时，本文提出的算法3 在DSC、SSC 压缩模块下的性能都优于R-WMMSE 算法。3 种模块的模型训练目标都是利用自身特定的映射结构，尝试将输入矩阵映射为一个性能更强的解。其性能提升机制和2.4 节末尾所考虑的特殊情况类似，但并不完全相同。在这种实验条件下，可学习模块的输出在提升目标函数值时，还需要对抗维度压缩的损失。不同的模块表达能力导致了不同的性能。

①FC 的参数量和复杂度都较高，性能方面反而表现较差。原因在于其参数量过多，结构过于复杂，导致泛化性较差。典型表现如图2 所示，当测试信噪比接近25 dB 边界时，使用信噪比-10～25 dB 数据训练出来的FC 模块性能显著下降。

②DSC 因其较强的输入输出关系表达能力和适中的参数量，具备最佳的性能。与FC 模块相比，DSC模块充分利用了输入矩阵的行列信息，左乘提取输入的行间特征（左乘矩阵的每一行可以视作一个特征提取向量），改变矩阵列空间，右乘则正好相反。

③SSC 相比DSC 具有更简单的结构，只能提取行间或列间关系，变换单边子空间，但是由于结构更简单，因此更不容易产生过拟合。在较低的复杂度下，仍然可实现良好的泛化性能。

从图2(b)可以看出，当压缩后的维度低于其秩时，3 种模块的性能相比图2(a)都有所下降，且全部比R-WMMSE 预编码更低。各模块的性能下降幅度不同，由于DSC 和SSC 的运算过程始终保持矩阵结构，过小的压缩维度将导致运算过程降低矩阵的秩，产生信息丢失，削弱这2 种矩阵模块的表达能力。相比之下，FC 模块则不受矩阵秩的影响。因此，和图2(a)相比，DSC 和SSC 的性能损失较大，而FC 的损失较小。然而，需要强调的一点是，预编码算法应用的核心指标是可达速率，如果可达速率不达标，那么继续降低交互量便没有意义。图2(b)中的结果表明维度压缩的损失较大，无法通过可学习模块完全补偿，因此需要采用更大的压缩维度。

图2 的结果表明压缩维度（前传交互流量）和性能之间存在折中。在保证性能的前提下，DSC 和SSC可以实现更好的预编码性能和压缩维度的折中。此外，在适当的压缩维度下，DSC、SSC 相比FC 展现出来的性能优势体现了2 种矩阵结构的模块设计的优势。

将X的维度压缩至16×16，并固定训练和测试的SNR 为20 dB，各算法的性能对比如图3 所示。对比各算法关于不同输入样本的性能范围，发现DSC 和SSC 的频谱速率在不同样本上的差异都在10 bit/(s·Hz)左右，而 FC 和 R-WMMSE 的差异都达到了15 bit/(s·Hz)。图2 和图3 的实验结果都表明，分布式算法框架和可学习压缩模块联合优化的模型，既从经典算法的计算结构中获得了“鲁棒的性能保证”，又依靠可学习压缩模块获得了“降交互和提性能”的潜力。

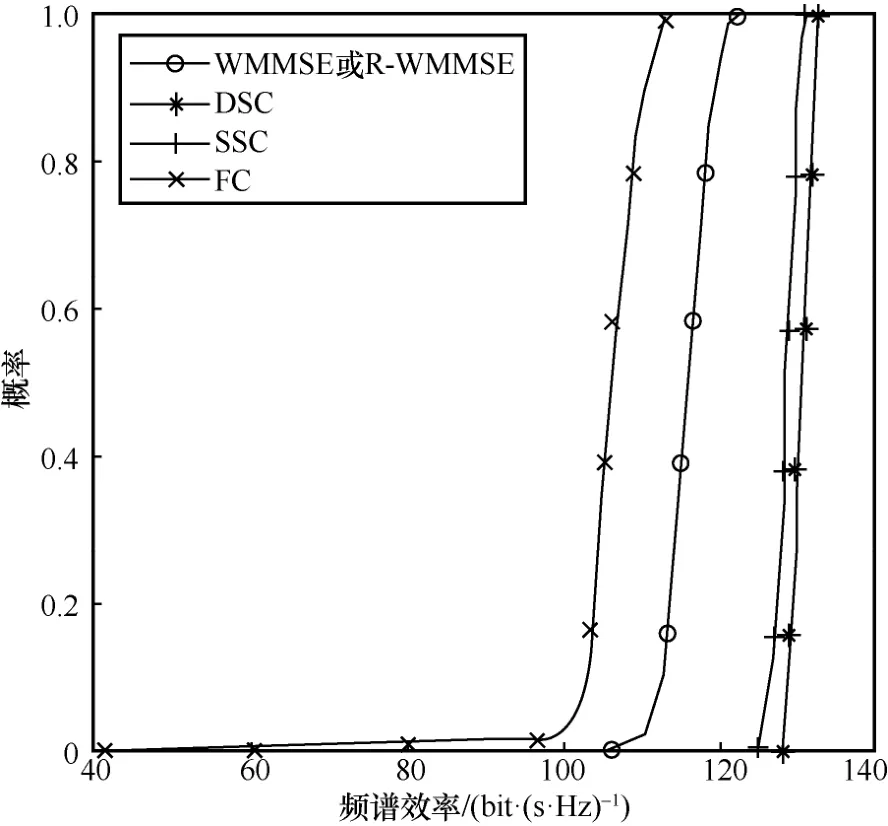
图3 固定SNR=20 dB 时各算法的性能对比

接下来，对比各算法的数据交互量和计算复杂度。表2 展示了各算法的前传流量大小。从表2 可以看到，本文提出的算法3 在不同的压缩模块下，数据交互量都比R-WMMSE 小。例如，当压缩维度为16×16 时，本文提出的算法3 的数据交互量比R-WMMSE 降低了多达25.0%。

表2 各算法的前传流量大小

表3 统计了各算法的复数乘法次数。从表3 可以看到，本文提出的采用DSC 和SSC 的分布式预编码算法在计算复杂度方面相比R-WMMSE 有相当大的优势，可以极大地降低基带处理的时延。例如，当压缩维度为16×16 时，采用DSC 的分布式预编码算法比R-WMMSE 的计算复杂度降低了52.9%。

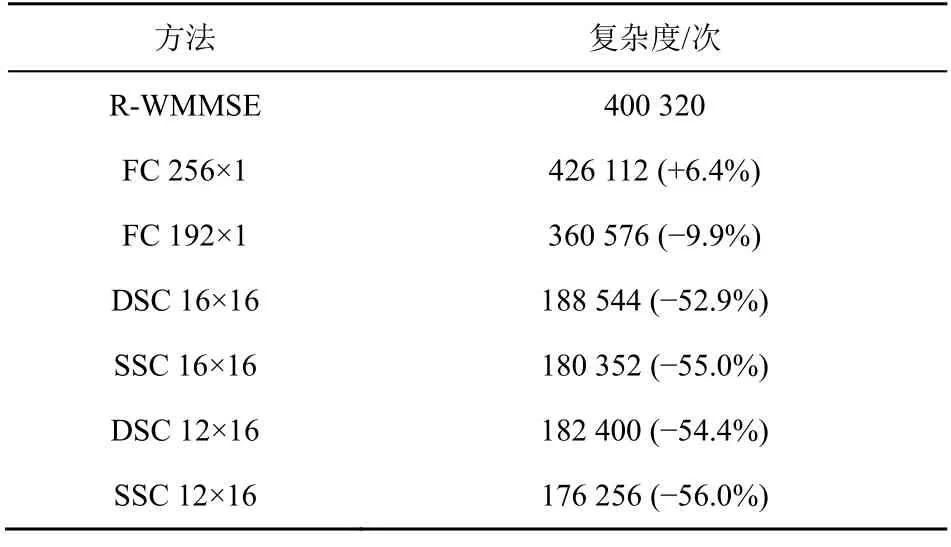
表3 各算法的复数乘法次数

最后，本文提供了一个参考策略，指导如何在应用中选择合适的模块。这包括选择合适的压缩维度和从SSC、DSC 中选出一种模块。模块的选择要满足系统的核心需求，例如，在本文所考虑的应用中，核心需求是性能和数据交互，前者保证系统的实用性，后者对应于模块的基本功能。压缩维度是影响这2 个指标的首要条件。如果系统对性能有严格要求，设计者可以测试SSC 和DSC 在不同压缩维度下的性能，找到符合性能需求的压缩维度。然后选择模块。如果在计算复杂度和模型存储（模型参数量）方面没有特别要求，选择DSC 即可；否则，可以根据计算复杂度和模型存储的具体表现进一步选择。总之，模块选择是一个帕累托最优点的选择问题，需要通过实验，根据系统对不同指标的要求程度做出权衡。

此外，一种经验性的选用策略是，在压缩维度方面尽量保证压缩后矩阵的秩不比原矩阵秩更低，模块选择方面在对计算复杂度和存储没有严苛要求的情况下选用DSC 模块即可，否则需要基于不同帕累托最优点的实验结果，根据性能指标的重要性进行权衡。

4 结束语

随着未来通信系统中基站天线数的持续增长，BBU 间进行信号处理的前传流量也将极大增加。为了降低前传数据交互，支持更大的天线阵列，本文提出了一种针对Massive MIMO 系统的通信高效的分布式预编码方案。该方案以R-WMMSE 分布式预编码作为算法框架，结合高效极简的可学习数据压缩模块设计，通过对两者进行联合优化，可以实现预编码性能和前传通信效率两方面的提升。仿真结果表明，相比于经典的WMMSE 预编码算法，本文的分布式预编码方案具有更好的性能和更低的数据交互要求。