水电站调压室托马临界稳定断面公式再认识

张 健，姚天语，王沁怡，仇为鑫，陈 龙，陈 胜

(1.水灾害预防全国重点实验室，江苏 南京 210098；2.河海大学 水利水电学院，江苏 南京 210098)

1 引言

动力系统运行稳定性在数学上有严格的定义，最早由俄国数学家李雅普诺夫 1892 年提出平衡点稳定、渐近稳定、不稳定概念，1933 年 Persidski 又提出了一致稳定性的概念；针对实际工程中常遇到的小扰动稳定、大扰动不稳定现象，1949年Massera提出了定范围渐近稳定性概念，1952年Barbashin和 Krasovski 进一步提出了全局渐近稳定性和全局一致渐近稳定性概念[1]。实际工程中的稳定性定义通常可这样描述：处于平衡态的动力系统会不可避免的受到各种扰动影响，如扰动消失后，扰动所产生的影响也随之逐渐消失，系统逐渐回复到未被扰动前的初始平衡态，则可认为该动力系统是稳定的；如扰动消失后，扰动所产生的影响并没有消失，而是导致系统越来越偏离初始平衡态，最终无法回复到未被扰动前的初始状态，则认为该动力系统初始平衡状态是不稳定的。动力系统的稳定性实际上是指动力系统某一工作状态下的稳定性。虽然实际应用中，人们往往会关注扰动产生的方式与大小，但这个问题与稳定性本质无关，只要一时性的激励产生了扰动就可以了，稳定与否取决于扰动之后的系统响应状态[2]。检验一个动力系统是否稳定，最简单的方法是给处于初始动力平衡态的系统施加微小扰动，分析系统受扰动后的动力响应，并判断动力系统是否能够恢复到初始平衡状态。

含调压室的水电站输水发电系统稳定性问题研究迄今已超过了百年。水电站输水发电系统常见的布置如图1所示，1904年德国Heimbach水电站在试运行中发现：当电站负荷较大时，调压室水位波动异常，出现了发散现象。托马(Thoma)教授针对该问题进行了研究，并于1910年提出了著名的调压室临界稳定断面公式——托马公式[2]。托马公式问世后百余年时间内，大批学者对公式适用性展开了大量的研究，最终得到的结果形式均是在托马断面公式的基础上加以改进，并乘以一个安全系数，而关于安全系数是否应该大于1还是小于1的讨论则一直延续至今。Schuller、Karas、Frank、Jaeger、季奎等人针对实际运行时调压室水位可能产生的扰动范围[3-4]，建议安全系数大于1.0，最大可达到2.0；董兴林、索丽生、孔昭年、杨开林等人考虑了调速器调节方式的影响[5-8]，Calame、Garden、刘启钊、杨建东、彭守拙、赖旭等人考虑了调压室底部流速水头及阻抗的影响[9-12]，均认为安全系数可小于1.0；Scimemi在3个带调压室的水电站开展了现场试验，试验结果表明，3个调压室均不满足托马断面，仍可稳定运行[13]；刘丹总结了回龙山、太平哨两座面积远小于托马断面的调压室实际运行情况，认为并网运行可以极大缩减托马断面[14]；1957年，Chevalier和Hug分析了Cordeac水电站的试验结果，认为调速器不可能保持出力不变，而是滞后20 s左右，并提出了“亚托马断面(sub-Thoma Section)”概念[13]；Evangelisti与Gradel分别考虑了水轮机效率对托马断面的影响，认为安全系数由水轮机运行工况点的实际位置决定，大小在1左右[13]；我国水电站调压室设计规范推荐的安全系数在1.0～1.1之间，如小于1.0，则需要进行运行稳定性与调节品质分析[15-16]。近年来，随着溪洛渡、白鹤滩等巨型水电站的陆续运行，在水机电一体化的基础上共同开展调压室稳定性问题的研究，已成为未来研究的发展趋势[17]。

图1 含调压室的水电站输水发电系统示意图

本次研究在前人成果基础上，仍采用托马断面推导过程中的假设，不同之处在于将托马公式推导过程中忽略的调压室后压力管道与机组后尾水道水体惯性重新予以考虑，进行结果对比，讨论托马公式的合理性。

2 托马(Thoma)临界稳定判别公式

2.1 含调压室动力系统基本方程(组)图1中，当水轮机引用流量发生变化时，调压室中水位及隧洞中流速均将发生变化，根据水流连续性定律，调压室处连续性方程为：

(1)

式中：Q1为调压室上游引水道流量，m3/s；Q2为调压室下游水道与机组的引用流量，m3/s；F为调压室面积，m2；ZT为调压室水位，m。机组处连续方程为：

Q2=Q3

(2)

式中Q3为机组下游尾水管道流量，m3/s。引水道至调压室水流动力方程：

(3)

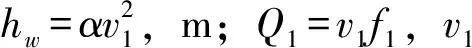
(4)

式中：HU为水轮机前测压管水头，m；hwm为调压室后压力管道水头损失，m；f2为调压室后压力管道面积，m2；L2为调压室后压力管道长度，m。水轮机至下游尾水道水流动力方程：

(5)

式中：HD为水轮机后测压管水头，m；hwd为水轮机后压力尾水管道水头损失，m；ZD为水轮机下游尾水水位，m；f3为水轮机后压力尾水管道面积，m2；L3为水轮机后压力尾水管道长度，m。

当系统出现扰动后，为保证出力不变，机组采用等出力调节模式，并假设机组前后流速水头相等、调节过程中效率不变，则等出力调节方程：

Q2(HU-HD)=Q20(HU0-HD0)=C

(6)

式中下标“0”表示对应变量的初始状态。

以上得到的6个方程中与常规教科书不同之处在于多了式(4)与式(5)，即考虑了调压室后压力管道与机组尾水管道的水体惯性。

未扰动前的初始恒定状态(平衡态)方程：

Q10=Q20=Q30=Q0

(7)

ZT0=ZU-hw0=HU0+hwm0

(8)

HD0=ZD+hwd0

(9)

HU0-HD0=ZU-ZD-hw0-hwm0-hwd0

(10)

2.2 含调压室动力系统小波动稳定分析方程(组)根据李雅普诺夫稳定性定义，可在含调压室的水电站输水发电系统中施加微小扰动，并在平衡点处进行线性化处理，将式(1)至式(6)非线性方程(组)简化为线性方程(组)。令：ZT=ZT0+z、Q1=Q10+q1、Q2=Q20+q2、Q3=Q30+q3、HU=HU0+hu、HD=HD0+hd。上述定义中，变量意义同前，扰动量均采用小写字母表示。

对等出力控制方程(6)进行线性化处理后，可得：

(11)

考虑式(7)至式(10)以及水头损失与流速的平方成正比，对式(1)至式(6)进行线性化处理后，并联立式(11)，可得描述含调压室的水电站输水发电系统的三阶线性常微分方程，其等价的一阶线性常微分方程组为：

(12)

式(12)可以表示为如下向量形式：

(13)

式(13)对应的特征方程为：

λ3+a1λ2+a2λ+a3=0

(14)

式(14)中：

(15)

(16)

(17)

忽略调压室至机组之间压力管道与机组之后尾水管道水体惯性，式(13)可简化为二阶动力系统：

(18)

式(18)对应的特征方程为：

λ2+b1λ+b2=0

(19)

其中：

(20)

(21)

线性化后含调压室水电站输水发电动力系统是否与原非线性系统具有同样的稳定性，李雅普诺夫给出了以下两个定理[1]：

定理一 若一次近似方程组的特征方程所有特征值实部均为负，则原方程零解渐近稳定。

定理二 若一次近似方程组的特征方程至少有一特征值实部为正，则原方程零解不稳定。

2.3 托马临界稳定断面判别公式讨论采用赫尔维茨(Hurwitz)—鲁歇(Rouche)判别法分别对动力系统式(13)、(18)进行稳定性判断。满足二阶系统稳定性的充要条件为：b1>0、b2>0，即：

(22)

(23a)

hw0+3hwm0+3hwd0>ZU-ZD

(23b)

式(23a)与式(23b)是“或”的关系，即满足其中任一式即可。对于水电站输水发电系统，水头损失过大是极不经济的，一般满足式(23a)、不满足式(23b)，条件b2>0可自动满足。需说明的是，通常的教科书中往往不提式(23b)，这样会给人造成误解，似乎水头损失大到一定程度，系统必将失稳。从下述的式(24)可以知道，如果系统的水头损失增大到能够满足式(23b)，则系统所需要的调压室稳定断面为负值，即水头损失大到一定程度，系统恒稳定。式(22)是著名的托马临界稳定条件，对应的面积称为托马面积。即：

(24)

式(23a)意味着系统水头损失增大到一定范围，系统将失稳，即水头损失对系统稳定的影响可能是不利的；而式(24)则表明，引水道水头损失系数α越大，所需要的调压室临界断面越小，即当调压室面积确定后，引水道水头损失的增加对稳定是有利的；式(23)与式(24)一起构成了系统稳定的充要条件，但它们各自反映的水头损失对稳定的影响却存在一定矛盾，这是托马公式带给人们的第一个困惑。其次，式(24)表明调压室后的压力管道与尾水道的水头损失对稳定是不利的，而几乎所有针对实际系统的小波动过渡过程数值分析表明，压力管道与尾水道水头损失的增加可显著加快波动衰减。调压室后的压力管道与尾水道的水头损失对稳定确实不利吗？为什么与实际数值计算情况不符？这是托马公式带给人们的第二个困惑。

满足三阶系统稳定性的充要条件为：a1>0、a1a2>a3、a3>0。这里我们重点关注条件a3>0，将其化简后，可得：

(25)

比较式(23a)与式(25)，不难发现，二者是互相矛盾的，由于式(23a)与式(25)分别是二阶系统与三阶系统稳定的充要条件，也就是说二阶系统与三阶系统稳定性几乎是截然相反的。对于实际输水发电系统，水道水头损失不可能超过静水头的1/3，即无论调压室后的压力管道与尾水道长短，只要构成了三阶系统，同时该三阶系统采用等出力调节运行方式，无论调压室断面多大，系统是恒不稳定的，调压室临界稳定断面不存在！这可能是托马公式带给人们最大的困惑。

本次统计主要涉及浙江省果树产业相关的观光采摘节的名称、举办地点、举办时间、首届举办时间、已举办届数、节庆的主题、节庆活动的主要内容等。

对于三阶系统，如果调压室面积无穷大，三阶系统还可简化为一阶的水库—水轮机系统，直接得到方程的扰动解：

(26)

式中：系统产生流量q0的初始扰动；qt为扰动产生后的发展过程，直接呈幂指数型式发散。式(26)从另一角度说明了等出力调节系统是不稳定的动力系统，不存在调压室临界稳定断面。

二阶系统来源于三阶系统的简化。教科书中曾经解释：对于含调压室的输水发电系统，L2、L3相对于L1较小，其内水体惯性可忽略不计，由此三阶系统可简化为二阶系统，从而在理论上得到了托马临界稳定断面。这种关于三阶系统可简化为二阶系统的解释比较牵强，从大量水电工程建设实际来看，L2与L3之和占比大都超过了L1的10%，对于抽水蓄能电站而言，由于水头相对较高，占比甚至可能超过50%。当然，这并不是本质性差别，L2与L3在电站输水系统中是客观存在的，将其忽略后得到的结论，如果只是涉及对结论的定量影响，而非颠覆性评价，这种忽略是可以接受的，但如果忽略后得到了完全相反的结论，这种忽略就值得商榷了。

3 弹性水体系统稳定性判别准则

以上关于托马断面的分析中，动力方程采用了刚性水体假设。对于含调压室的输水发电系统，等出力调节模式下，刚性水体是不可能稳定的，从式(26)的结果可以看出，这是一个显见的结论。主流的学术观点认为调压室后的压力管道与机组后的尾水道属于弹性水体范畴，弹性水体中压力变化主要由水锤波引起，水锤波在压力管道中的传播反射，导致了管道中的压力、流量在空间上的不均匀分布，从而使研究变的非常复杂。直接采用调压室水位变化近似反映机组水头变化，尽管得到了一些与常识不符的结论，但毕竟也是解决问题的一种途径，这估计是百余年来人们一直致力于托马公式的改进而不愿意放弃的主要原因。

对于实际弹性水体的有压输水系统，如果考虑调节过程中压力管道中水锤波的传播与反射，等出力调节模式下，系统是否能够稳定，尚需要慎重分析。实际弹性水体的压力管道水流动力方程与连续方程分别为[2]：

(27)

(28)

式中：H为测压管水头，m；D为管道直径，m；f0为达西-威斯巴哈摩阻系数。式(27)、式(28)为一组双曲偏微分方程，忽略管道摩阻后，其通解为：

(29)

(30)

(31)

(32)

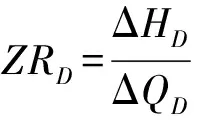
(33)

式中γ为管道水锤传播常数，s/m。式(31)(32)(33)联立可得：

rUrD=e2γL

(34)

对于无摩阻系统，水力振动传播常数γ可写为：

(35)

式中：ω为管道中自由振动谐振频率，弧度/s；σ为对应谐振频率的衰减因子，为实数；i为虚数单位。对于一个稳定的系统，扰动所产生的水力自激振荡均应最终消失，即σ≤ 0。由式(34)(35)可得到考虑水锤传播反射特性的弹性系统稳定性判断准则：

(36)

式中：水锤反射系数rU与rD均为复数；下标i为组成系统的各管段。式(36)表明，如系统稳定，组成系统的各管段进、出口端水锤反射系数的乘积的模(绝对值)须小于1。式(36)虽然是针对无摩阻系统得到的，但对于实际的有压水力输送管道而言，摩阻并不大，该公式的适用范围还是较广的，是满足有压输水系统不发生水力自激振动的充分条件。

含调压室的水电站动力系统由上游引水道、压力管道、下游尾水道组成，则式(36)可写为：

|rU1rD1|<1

(37)

|rU2rD2|<1

(38)

|rU3rD3|<1

(39)

以上三式中，rU1、rD3分别为上、下游水库端水锤反射系数，均为-1；rD1、rU2分别为调压室上、下游水锤反射系数；rD2、rU3分别为机组上、下游水锤反射系数。调压室处水力阻抗满足[2]：

(40)

式中ZRD1、ZRU2、ZRT分别为调压室上、下游端与调压室的水力阻抗，s/m2；调压室处水力阻抗为：

(41)

式中s为拉普拉斯变量，s=σ+ iω，系统如稳定，该值须小于0。根据水力阻抗与水锤反射系数之间的关系，由式(40)可以得到：

(42)

(43)

式中θD1、θU2分别为复变量rD1、rU2对应的幅角。由于上游水库端rU1=-1，如满足条件式(37)，则：

|rD1|<1

(44)

由于式(43)中，ZRC1、ZRC2、1+|rD1|2+2|rD1|cosθD1、1+|rU2|2+2|rU2|cosθU2均大于0，σ小于0，故可得：

|rU2|>1

(45)

故如满足条件式(38)，则：

|rD2|<1

(46)

等出力调节模式下，水轮机上、下游侧的水力阻抗应满足：

(47)

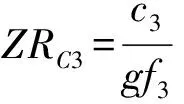
(48)

式中θD2、θU3分别为复变量rD2、rU3对应的幅角。由于下游水库端rD3=-1，如满足条件式(39)，则：

|rU3|<1

(49)

|rD2|>1

(50)

显然，式(50)与式(46)是矛盾的，这也就证明了在等出力调节模式下，式(37)至式(39)不可能同时满足，即对于实际弹性水体，系统一旦出现扰动，在等出力调节模式下，扰动引起的水锤波在管道中不断传播反射，最终会导致系统出现发散的水力振荡。

式(36)虽然没有直接体现出管道摩阻的影响，但反射系数的本质与来源反映了扰动引起的水锤波在管道中来回反射，水锤波消失则扰动消失，管道中摩阻的存在是导致水锤波衰减的重要因素之一[2]，摩阻相应起到了等效减少管道两端水锤反射系数模大小的作用，由此可直观上判明管道摩阻对系统稳定性影响是有利的，并不存在教课书上“调压室前的引水道摩阻对稳定有利、调压室后的压力管道与尾水管道摩阻对稳定不利”的结论，没有考虑管道摩阻的弹性水体稳定性判别公式(36)属于偏安全的稳定性判据，是系统稳定的充分条件。

4 算例分析

采用图1中含调压室的水电站输水发电系统，其中：

ZU=100.0 m，ZD=0.0 m，Q10=Q20=Q30=Q0=40.0 m3/s，L1=2000.0 m，L2=L3=200.0 m，f1=f2=f3=10.0 m2，hw0=2.0 m，α=0.125 s2/m，hwm0=0.5 m，hwd0=0.5 m，c1=c2=c3=1000.0 m/s，调压室面积F=2.33×Fth=2.33×(2000.0×10.0)/[2.0×0.125×9.8×(100.0-2.0-3×0.5-3×0.5)]≈200.0 m2。

分别采用文中的二阶刚性水体模型、三阶刚性水体模型、弹性模型来验证系统小波动稳定性。其中弹性模型为式(27)(28)联合构建的偏微分方程组，通过特征线法数值求解；二阶刚性水体模型与三阶刚性水体模型均为常微分方程组，为了充分考虑实际系统中非线性项的影响，不采用式(12)、式(18)建立的线性化模型，而是直接通过式(1)至式(10)建立非线性模型，采用四阶龙格—库塔法进行数值求解。其中，二阶刚性系统的动力模型为：

(51)

三阶刚性系统的动力模型为：

(52)

三种模型的系统扰动均为上游水库的水位变化，假设水库水位先1 s内线性上升5 m，然后1 s内线性回落至原水位，如图2。

图2 水库水位扰动过程

图3与图4反映了正常摩阻情况下，在系统发生小扰动时刚性二阶模型的调压室水位与机组流量变化过程。由于调压室面积为托马断面的2.33倍，调压室水位与机组流量变化过程均是收敛的，计算结果与理论分析相吻合。

图3 调压室水位变化过程(刚性二阶模型)(F=200 m2)

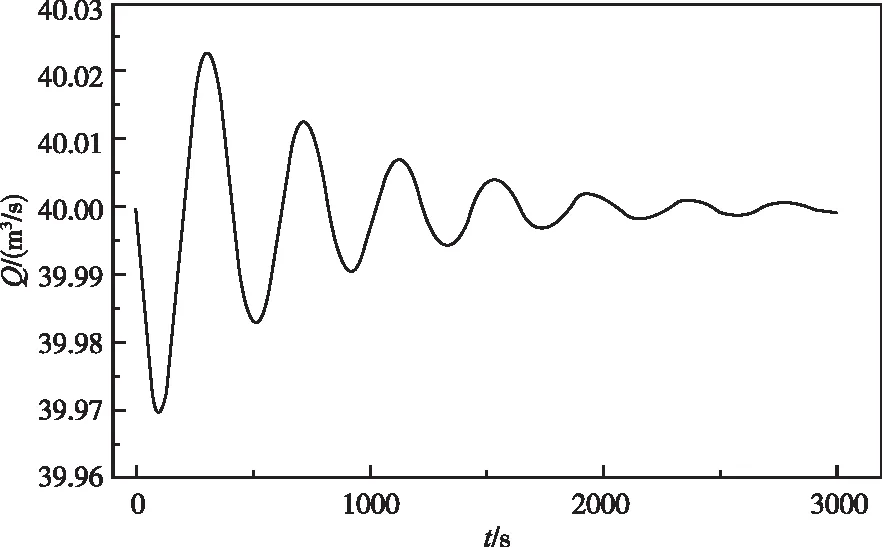
图4 机组流量变化过程(刚性二阶模型)(F=200 m2)

图5与图6是人为将水头损失加大后，系统发生小扰动时刚性二阶模型的调压室水位与机组流量变化过程。由于水头损失分别达到hw0=10.0 m、hwm0=12.5 m、hwd0=12.5 m，简单计算可以知道，此种水头损失组合下既不能满足式(23a)、也不能满足式(23b)，其中：调压室面积仍取200.0 m2，对应的托马面积安全系数约1.83，由于采用了非线性模型，扰动过程并没有发散。但从模拟结果可以看出，初始工况点的调压室水位90.0 m，机组流量40 m3/s，而扰动后终了工况点的调压室水位90.94 m，机组流量38.06 m3/s，二者虽然差距不大，但初始工况点显然不满足李雅普诺夫稳定性定义，这与二阶系统理论预测是相符的。初始工况的总水头损失：hw0+hwm0+hwd0=35 m>100/3 m，不满足式(23a)，终了工况点总水头损失：hw0+hwm0+hwd0=31.7 m<100/3 m，满足式(23a)；对于二阶系统而言，意味着随着水头损失加大，初始工况点逐渐不稳定，最终会发散到另外一个稳定的工况点。

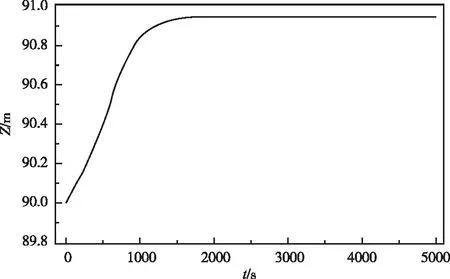
图5 调压室水位变化过程(刚性二阶模型)(F=200 m2)

图6 机组流量变化过程(刚性二阶模型)(F=200 m2)

图7 调压室水位变化过程(刚性三阶模型)(F=200 m2)

图8 机组流量变化过程(刚性三阶模型)(F=200 m2)

图9 调压室水位变化过程(刚性三阶模型)

图10 机组流量变化过程(刚性三阶模型)

图11 调压室水位变化过程(弹性模型)(F=200 m2)

图12 机组流量变化过程(弹性模型)(F=200 m2)

图13 调压室水位变化过程(弹性模型)

图14 机组流量变化过程(弹性模型)

图7与图8反映了正常摩阻情况下，在系统发生小扰动时刚性三阶模型的调压室水位与机组流量变化过程，由于采用了非线性模型，扰动过程并没有发散。从模拟结果可以看出，初始工况点的调压室水位98.0 m，机组流量40 m3/s，而扰动后终了工况点的调压室水位45.75 m，机组流量208.33 m3/s，二者差距甚远，显然不满足李雅普诺夫稳定性定义，终了工况点的水头损失远超过了水头(100 m)的1/3，虽然不具备现实意义，但却恰反映了三阶系统稳定性判据式(36)正确性。

图9与图10是人为将水头损失加大后，在系统发生小扰动时刚性三阶模型的调压室水位与机组流量变化过程，摩阻增大到特定程度(仅具有理论意义)后，系统得以稳定。

图11与图12反映了正常摩阻情况下，在系统发生小扰动时弹性模型的调压室水位与机组流量变化过程，考虑了水锤影响后的波形几乎与刚性三阶模型中的图7与图8完全一致，虽然没有发散，但初始工况点出现了大幅转移，同样也是不稳定的，结果符合弹性模型系统稳定性判断准则式(27)。

图13与图14是人为将水头损失加大后，在系统发生小扰动时弹性模型的调压室水位与机组流量变化过程，摩阻增大到特定程度(仅具有理论意义)后，系统得以稳定。由于系统参数选取相同，计算得到的波形与刚性三阶模型中的图9与图10非常相似。

从图3至图14可以看出：在等出力调节方式下，针对含调压室的水电站输水系统稳定性判断，刚性二阶模型与刚性三阶模型及弹性模型得到的结果完全相反，且只有将系统摩阻增大到特定程度(理论层面)后，刚性三阶模型与弹性模型才能稳定，且无论稳定与否，刚性三阶模型与弹性模型计算结果与波形都极其相似。刚性二阶模型中，摩阻大系统反而失稳，与人们的直观认识相悖；刚性三阶模型、弹性模型中，摩阻大系统稳定性更好，说明摩阻有利于对稳定，与人们的直观认识相符。另外，弹性水体模型中由于水锤波与摩阻的综合影响，无论是扰动过程中的调压室水位波动过程还是机组流量变化过程，虽然收敛速度更快，但曲线的光滑性较刚性模型差，存在一定程度的“毛刺”现象，客观上反映了短周期水锤波与长周期调压室涌浪的共同作用，也与实际观测结果相符。

图9与图10、图13与图14同时也反映了刚性三阶模型与弹性模型下不同调压室面积(30 m2、200 m2、300 m2)对稳定的影响，结果表明，调压室面积大范围的变化并没有给系统稳定造成实质性影响，只是在扰动周期、扰动衰减程度上存在一定差别。含调压室的输水发电系统内水体振荡类似常见的U型管振荡，如要保证U型管内水体在振荡过程中不溢出来，首先是控制U型管振荡方式(类似等出力调节)；其次是对管内水体运动的抑制(加大摩阻)，增加U型管面积并不是有效的方式。

5 结论

在理论上指出了托马临界稳定断面公式的缺陷：托马公式基于刚性水体假设，忽略调压室后压力水道与尾水道的水体惯性，从而将实际上不可能稳定的三阶动力系统简化为了相对稳定的二阶系统，由于压力水道与尾水道是水力机组不可或缺的天然属性，这样得到的结论并不具备工程设计指导意义。

含调压室的水电站输水发电系统运行稳定性主要取决于水轮机上下游侧的水锤反射系数，而非调压室面积；无论是调压室前引水道还是调压室后的压力管道与尾水道，摩阻对稳定性影响均是有利的，并不存在教科书上“调压室前的引水道摩阻系数增加对稳定有利、调压室后的压力管道与尾水管道摩阻对稳定不利”的结论。

等出力调节模式下，无论是采用刚性水体假设还是针对实际弹性水体，实际工程中含调压室的水电站输水发电系统一定是不稳定的，系统稳定性意味着系统可实现性，一个不稳定的系统不可能存在稳定断面，据此得到的托马临界稳定断面在理论上是不成立的。

取消托马临界稳定断面的制约，一方面可为水电站调压室设计带来了更高的灵活度与自由度，但另一方面也对水轮机调节控制机构可靠性提出了更高的要求。调压室设计需要结合工程实际布置与运行方式，具体问题具体分析，确保工程安全。