水风光互补系统装机容量配置解析优化及敏感性分析

陈祥鼎，刘 攀，吴 迪，马 黎，龚兰强，黄康迪，3

(1.武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072；2.中国电建贵阳勘测设计研究院有限公司，贵州 贵阳 550081；3.中国长江三峡集团有限公司科学技术研究院，北京 100038)

1 研究背景

大力开发清洁能源是我国实现双碳目标的重要途径[1-2]。以风能和太阳能为代表的清洁能源具有分布广泛、资源丰富和建设周期短等优点，然而由于易受环境条件影响，单独的风光出力因波动性较强无法被电网消纳，会产生严重的弃电[3-4]。由于水电储能和调节性能优异[5]，且水电、风电和光电出力具有天然的日内、年内互补特性[6]，逐渐形成了三种能源联合运行打捆送出的模式，即流域水风光多能互补系统[7-8]，该系统可以有效克服流域内风光电的送出和消纳难题[9-10]。

混合可再生能源规划设计事关互补系统的经济性、安全性和稳定性，包括确定电力系统的最佳配置、特定节点的发电机组的最佳位置、类型和尺寸等，使系统以最低成本满足负荷要求[11-13]。装机容量作为互补系统中的关键参数，直接关系到系统运行的可靠性与经济性[14]。配置规模过小会导致资源无法被充分利用而浪费，而过大又会使过剩的风光电无法被消纳而提高系统的投资成本。

目前，多能互补系统容量配置方面的相关研究主要利用数值模拟方法开展，主体框架是：以系统的整体经济效益最大或新能源电力消纳最优为目标构建装机容量优化数值模型，综合考虑系统的水风光资源约束、功率输出约束、负荷约束等条件，并选用如动态规划、遗传算法求解，从而配置风、光最优接入规模。如张舒捷等[15]构建了一种以实现经济效益最大化为目标的水光电站容量优化模型，选用遗传算法对光伏容量配置寻优；宋士瞻等[16]考虑风电和光伏多个约束构建了风电和光伏效益最大模型以优化装机，研究表明风电和光伏的最优装机差异较大。Fang等[17]通过最大化全生命周期的净收入，提出了一种集成到水电站中的光伏电站优化装机容量的方法，研究选择目前世界上规模最大的龙羊峡水电-光伏发电项目作为案例，计算了不同出力情景下的最优光伏装机容量。Ming等[18]提出了一个同步确定水光系统光伏容量和长期运行规则的框架，实例研究验证了该框架的有效性。Yang等[19]开发了一个气候水文运行框架，确定在气候变化条件下适合并入水电系统的光伏电站容量，研究表明在一定的装机容量范围内互补系统有良好的适应气候变化的运行能力。

然而，以往的研究方法计算过程复杂，难以明晰经济技术参数与最优装机容量和互补系统净效益之间关系，而解析优化方法只需获取少量参数即可进行容量配置，并能够量化最优装机、互补系统净效益对上网电价、装机成本等各经济技术参数的敏感性，有助于明确装机规划中各要素之间关系，为未来经济技术参数变化情形提供装机规划调整策略。

鉴于上述问题，本文耦合短期弃电规律、中长期优化调度、成本-效益分析模型，提出了一种装机容量配置解析优化方法，定量分析装机规划与经济技术因素内外两方面对系统总效益影响。首先，建立耦合短期弃电的中长期优化调度模型求解风光弃电率函数；其次，解析基于该函数的成本-效益模型推求最优装机函数，并与数值模拟方法比较以检验合理性；最后，进一步解析最优装机函数分析装机规划中的各经济技术参数敏感性。以雅砻江流域二滩水电站及周边风光系统为研究对象，检验所构建解析优化方法的可行性和合理性。

2 研究方法

2.1 风光弃电率函数和传统水电站存在弃水类似，水风光互补电站中普遍存在弃风、弃光的情况。当互补系统的出力大于该时刻负荷需求，或超出了电网输送能力就会产生弃电。由于风电、光伏功率与装机容量成线性关系[20]，扩大风光装机规模会使实际风光出力也相应地线性增加，在水电调节能力有限的情况下风电弃电率、光伏弃电率也会相应提高，因此本研究做出假设：在一定装机范围内，风电多年平均弃电率与风电装机呈线性，光伏多年平均弃电率与光伏装机呈线性。

(1)

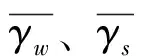
(1)模拟短期弃电：基于水电、风电和光伏的日内、年内特性考虑了汛期和非汛期两种基本弃电情景如图1，进而构建弃电损失模型模拟不同装机容量下对应的弃电损失函数，该函数可表征月平均水电出力与风光弃电率之间的关系。

图1 短期弃电情形

(a)汛期水库水位达到上限值(汛限水位或正常高水位)，入库流量较大使发电流量也取到上限时，此时无法降低水电出力[21]。为了满足互补电站出力与负荷需求间的平衡必须弃掉多余风光电。

(b)非汛期存在可调节库容时，水电出力达到下限值无法继续降低时，互补电站的出力仍然大于负荷需求，此时必须弃掉多余的风光电。

(2)中长期模拟水电出力：为模拟水风光互补系统各调度时段内水电出力，建立了以互补系统多年净发电量最大为目标函数的中长期优化调度模型：

(2)

(3)

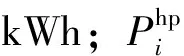
模型综合考虑的约束条件包括水量平衡约束、库容约束、发电流量约束、边界条件约束、保证出力约束、非负约束等，利用惩罚系数约束系统保证出力，目标函数更新为式(4)。利用动态规划对该模型进行求解，决策变量设定为水位，调度时段为月尺度。

(4)

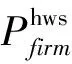
(3)统计逐时段弃电量：将模拟出的各调度期内平均水电出力回代入弃电损失函数，统计各时段内风光弃电量，进而推求多年平均风光弃电率与装机容量的关系如式(5)，拟合求取式(1)中的各系数。

(5)

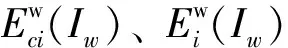
2.2 最优装机函数技术经济分析是确定风光装机容量的一种通用框架，该框架通过对互补系统全生命周期成本和收益评估开展优化设计。除了运行成本之外，全生命周期成本通常还包括资本成本和维护成本两个部分，统称为“固定成本”。在计算成本时，还必须考虑货币价值随时间的变化。在所有可能的互补系统容量配置中，具有最大净现值的配置被称为最优配置[13]。

需要明确的是，由于本文中水电站已经建成并投产运行，水电收益不影响风光装机，因此构建的成本-效益模型中：风光发电收益为收益的唯一来源，区分了风电、光伏上网电价的差异，并假定电价在互补电站运行期间不随时间变化；成本包括初始投资成本和运行维护成本，初始投资成本为装机容量与单位装机成本的乘积，运行维护成本来源于机组维修、检测等多方面，为风光发电量与单位发电量运维成本的乘积[17]，对净效益折现以考虑货币价值随时间的变化。模型以互补系统全生命周期净现值最大为目标函数。

(6)

(7)

式中：NRws为互补电站全生命周期净效益，NRw、NRs为风能电站、光伏电站净效益，元；Y为风能电站、光伏电站运行寿命，年；Bw、Bs为风电和光伏上网电价，元/(kWh)；Cin，w、Cin，s分别为风能电站、光伏电站的装机成本，元/kW；Com，w、Con，s分别为风能电站、光伏电站的运行成本，元/(MWh)；Iw、Is为风电和光伏的装机容量，MW；Pw、Ps为风电和光伏发电量，kWh；βw、βs为风电、光伏多年平均出力系数；dr为折现率；T为一年的运行小时数。

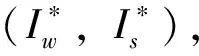
(8)

(9)

可以看出，最优装机函数形式十分简洁，在各规划参数已知的情况下，只需获取该地区风光多年平均出力系数和求解弃电率函数，即可计算与原有水电站相配套的风光装机容量。如计算结果为负值，表明从经济角度出发该地区不适合风光互补电站的建设。

2.3 经济技术参数敏感性在装机规划中，经济技术参数主要包括风光上网电价Bw、Bs，风光装机成本Cin，w、Cin，s，风光运行维护成本Com，w、Con，s和多年折现系数a。在实际情况下，各参数时刻受到政策、经济、技术等因素影响而并非恒定不变，同时式(9)表明各参数的变化会改变系统的最优装机容量，同时对互补系统的经济效益产生显著影响。因此，有必要进行敏感性分析获得对最优装机和系统净效益敏感和不敏感的参数，以应对未来时期内各参数变动带来的影响。

为准确量化各参数在原有情况变动下对最优装机容量的影响，对式(9)在最优装机容量值处泰勒展开得式(10)—(13)，代入已知其他参数可直接解析相关变量的敏感性。联立式(8)(9)可得到系统净效益与经济技术参数的关系如式(14)。

(10)

(11)

(12)

(13)

(14)

上式表明，最优装机与上网电价呈非线性正相关，与装机成本、运维成本呈线性负相关，与多年折现系数呈线性正相关。除上网电价外，互补系统净效益与各其他参数均呈二次函数关系。

3 研究对象

3.1 对象概况本文的研究对象为雅砻江下游由二滩水电站及周边风光电站组成的水风光互补系统，其坐落于四川省西南边陲攀枝花市，距雅砻江与金沙江的交汇口33 km。二滩水电站属季调节水库，是一座以发电为主的水利枢纽，兼有其他综合利用效益。其控制流域面积约11.64万km2，约占雅砻江流域面积的90%。二滩水电站特征参数见表1。

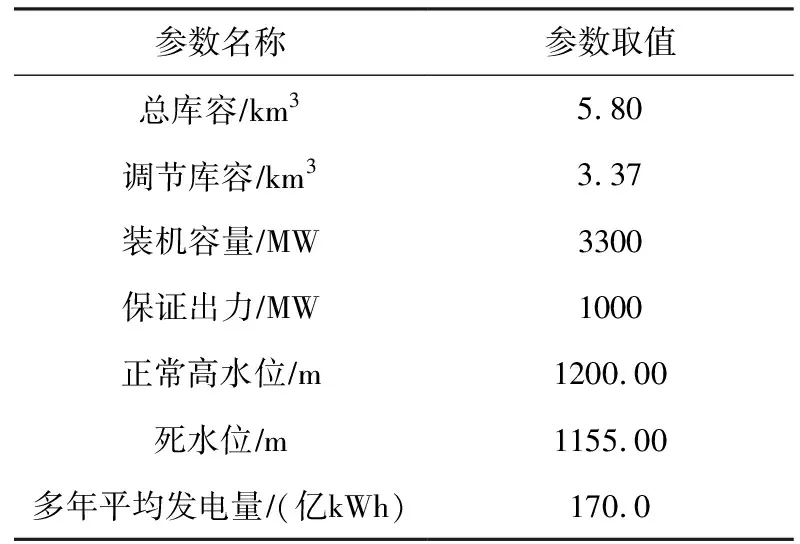
表1 二滩水电站特征参数

3.2 研究数据及方案设置研究数据包括：①二滩水电站1980—2010年共31年月尺度入库径流；②盐边站1980—2010年小时尺度辐射及气温资料；③盐边站1980—2010年小时尺度风速资料；④典型年(2016年)实测径流、辐射、气温及风速数据；⑤水电站典型日负荷曲线。其中，风速、辐射和气温资料来源于EarthDATA官网(https://disc.gsfc.nasa.gov/datasets)，径流资料由二滩水电站提供。绘制了长系列数据的箱线图如图2。由图可知，在年时间尺度内，风电和光伏出力具有一定互补性，且风光捆绑出力与水电出力也有较好互补性。流域内径流季节差异很大，汛期(5—9月)来流充沛，非汛期(10月—次年4月)流量较小。

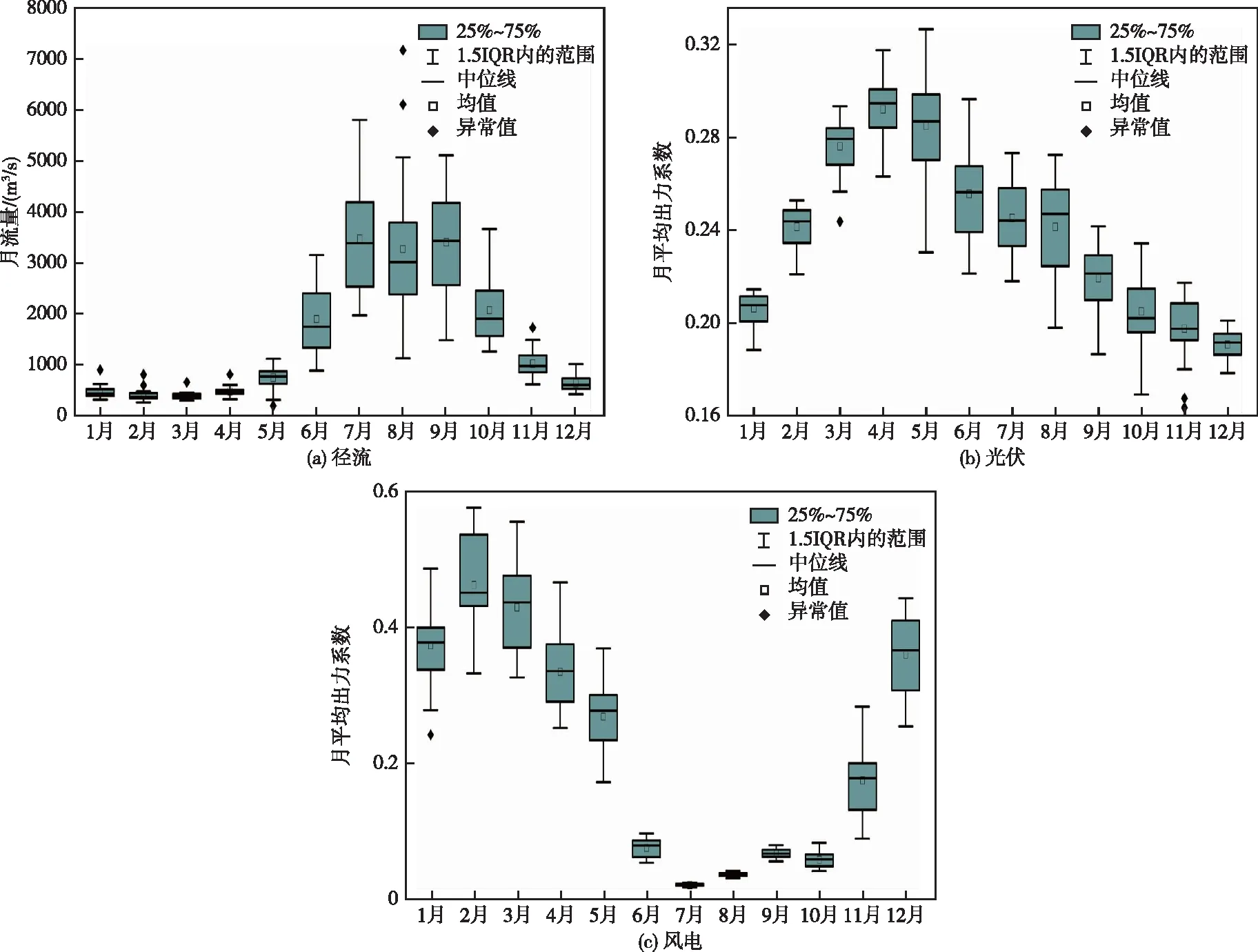
图2 长序列数据箱线图

考虑到水风光互补系统中水电作为调节电源消纳风光出力的波动，将风电装机和光伏装机容量下限均设置为100 MW，上限为2000 MW，取离散步长为100 MW，共生成400种装机情景。对于所有的装机组合，首先利用1980年1月—2010年12月的入库径流及风光出力资料进行优化调度计算，获得31年长系列调度样本，利用动态规划进行调度计算时，水库起调和终止水位均设置为1200.00 m，综合考虑计算效率和准确度，将水位离散精度设置为0.20 m。

二滩流域的风光电站规划参数及经济参数如表2，表中数据由雅砻江流域水电开发有限公司提供。

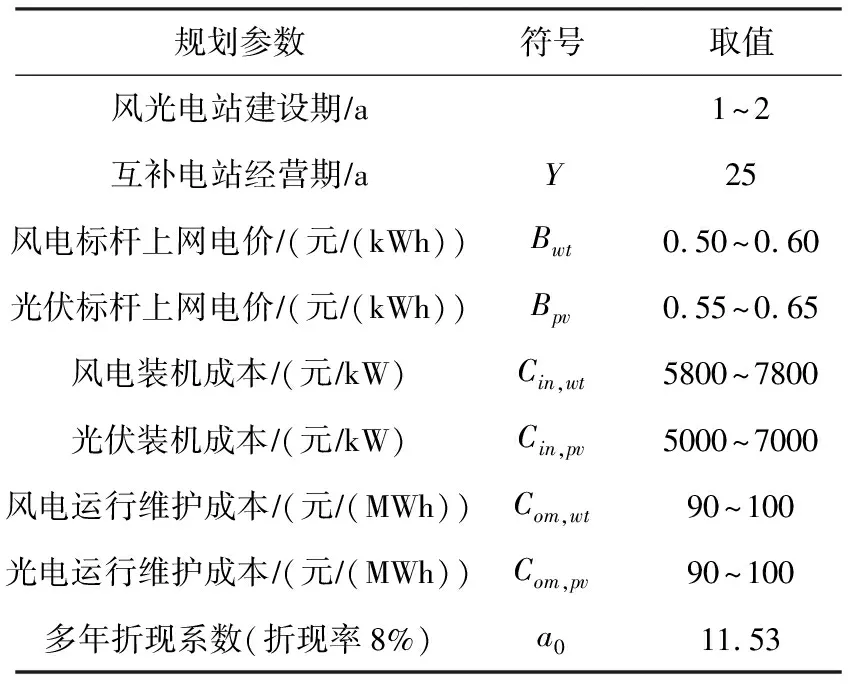
表2 风光电站规划参数及经济参数

4 研究结果

4.1 风光弃电率函数基于中长期时段水风光互补调度结果，计算统计了不同风光装机组合下的水电出力和弃电量，绘制结果分别如图3和图4。

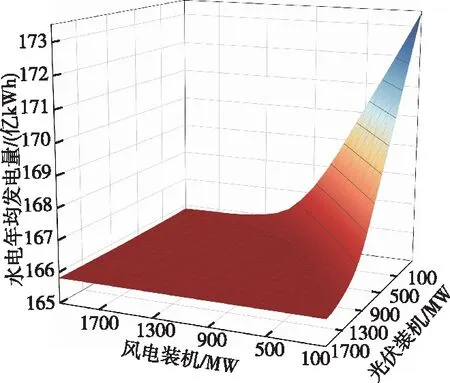
图3 不同装机组合对应的水电站年均发电量

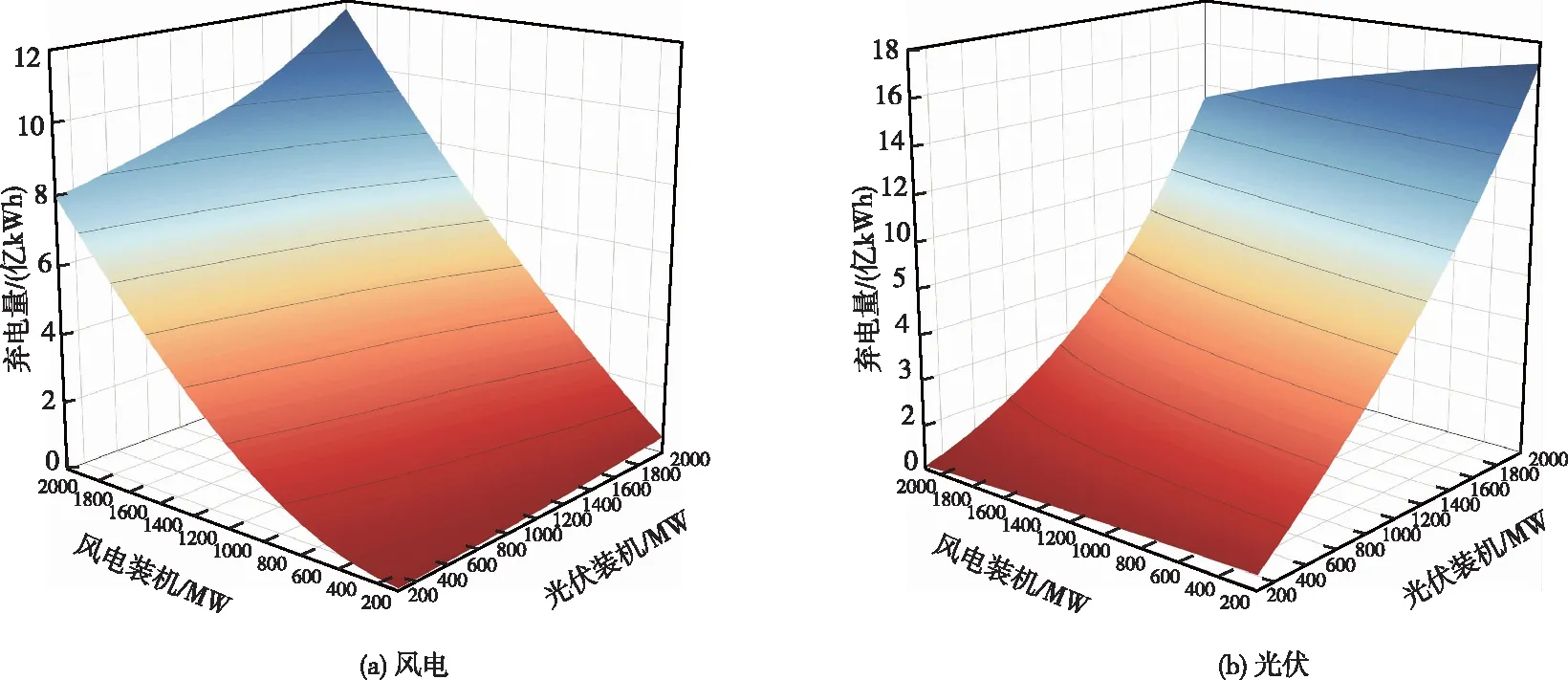
图4 不同装机组合对应的弃电量

图3中，随着风光装机容量增大，水电年发电量反而减小。在风光装机较小的情景下，水电发电量减小尤为明显，当增大到一定程度时保持一个固定值不再降低。原因在于负荷一定的情况下，风光装机增大提升风光上网电量的同时，水电站保证出力会发生相应变化，水电出力受到一定程度的抑制。

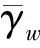
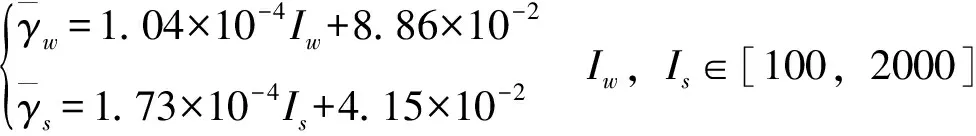
(15)

风光弃电率函数中包含斜率和截距两类参数，受互补电站日负荷、多年平均径流及风光出力系数等多因素影响，在风光多年平均出力系数差异不大的前提下，二者斜率较大差异原因在于光伏日内波动更大，弃电较风电更多。

4.2 最优风光装机容量将风光弃电率函数中的参数取值及表2中各经济技术参数代入式(7)中计算最优风光装机容量得：风电最优装机为1062 MW，光伏最优装机为1260 MW，风电弃电率为19.91%，光伏弃电率为25.99%，最大经济效益为52.34亿元。

对该结果采用数值模拟优化的方法进行检验：对于每种装机组合的长系列1980—2010年共31年数据，采用滑动窗抽样方法抽取了25年的调度数据输入至成本—效益分析模型，获取了最优风光装机容量和最大净效益值。两种方法及已有规划结果比较如表3，解析优化结果与数值优化相比误差为3.26%，与已有规划的风光装机数据也较为接近，表明该结果具有较强合理性，该解析方法行之有效。

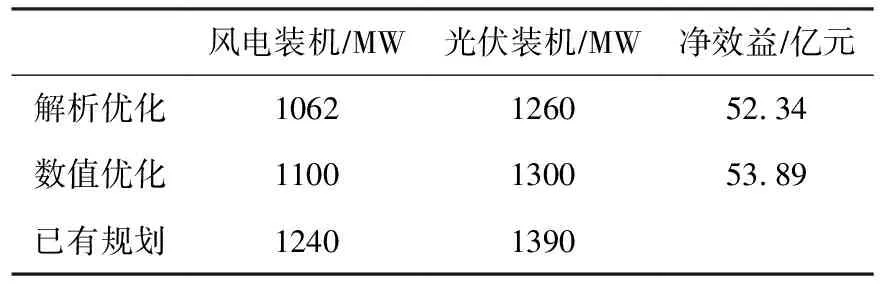
表3 最优装机容量比较

4.3 经济技术参数敏感性分析在原有经济技术参数附近的区间内，绘制了最优装机容量与各经济技术参数的关系曲线如图5。

图5 最优装机与各经济技术参数关系

对于式(8)—(11)，为比较不同经济技术参数对装机容量和互补系统净效益的敏感性，假设赋予各参数相较原参数相同变化幅度1%，计算结果如表4。

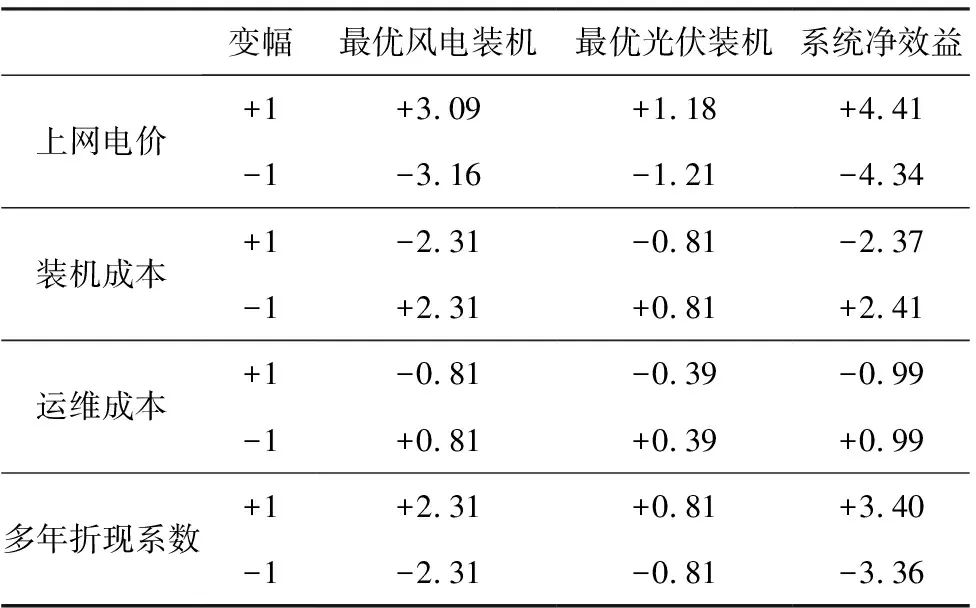
表4 敏感性分析结果 (单位：%)

对于最优装机，最敏感的参数是上网电价，最不敏感的则是运维成本，装机成本和多年折现系数对装机容量的敏感性相同但呈现相反影响。从表4知：风电上网电价增加1%装机将增加3.09%，运维成本增加1%装机将减小0.81%；光伏上网电价增加1%装机将增加1.18%，运维成本增加1%装机将减小0.39%，说明风电装机受经济技术参数影响更大。

对于互补系统净效益，各参数按敏感性排序依次是：上网电价、多年折现系数、装机成本、运维成本。同样得：每增加1%的风电和光伏上网电价，可提升4.41%的净效益；而运维成本降低1%对系统净效益的提升只有0.99%，说明互补系统的经济效益受政策和市场因素影响较大，受技术因素影响相对较小。

5 结语

深入研究流域水风光互补系统装机容量配置问题对未来我国水风光一体化可再生能源基地的规划建设具有重要指导意义。本文提出装机容量配置的解析优化方法，以雅砻江流域二滩水电站及周边风光互补工程开展了实例研究，主要结论如下：(1)长时段内风电、光伏弃电率与对应装机容量可用线性正相关关系描述；(2)该解析优化方法经数值模拟检验误差为3.26%验证了合理性，可为流域水风光互补系统装机容量配置提供技术支撑；(3)最优装机和互补系统净效益均对上网电价最敏感，对运行维护成本最不敏感，最优装机对装机成本和多年折现系数二者敏感性相同，净效益对上网电价敏感性为运维成本的4.44倍，可为未来经济技术参数变化情形提供装机规划调整策略。需要指出的是，本研究对流域水风光互补系统装机容量的解析优化方法进行了初步探索，但如何定量分析弃电率函数参数的影响因素以及制定合理的互补系统分期装机方案，有待进一步研究。