基于角域重采样的宽度迁移学习算法＊

齐晓轩 王 珊

（①沈阳大学应用技术学院，辽宁 沈阳 110044；②沈阳大学机械工程学院，辽宁 沈阳 110044）

轴承是旋转机械中最重要的部件之一，其运行状态直接关系到整个机械系统的安全。同时，由于其工作环境复杂，因此轴承也是最容易损坏的零件之一。所以，有必要对轴承的工作状态进行故障诊断和监测。

实际应用中，轴承的工作条件经常变化，在变转速等工况下采集到的信号通常为非平稳信号，导致无法获取到精确的轴承故障特征信息，难以对轴承故障精确诊断。因此，需要对采集到的非平稳信号进行平稳化处理，为后续操作奠定基础。

阶比分析是处理非平稳信号的有效方法，其原理是通过角域重采样将非平稳的振动信号转换为平稳的角域振动信号，然后在恒速下进行故障特征提取。宫涛等人首先通过阶次分析方法将非平稳信号变换为平稳信号，然后增强了故障特征阶次，最后实验表明提出的方法具有一定的优越性[1]；刘鲲鹏等人首先通过角域重采样方法将变转速信号转换为角域平稳信号，最后识别故障特征阶次，试验表明提出的方法是有效的[2]；吴剑等人通过角域重采样方法将非平稳信号变成了平稳信号，然后利用小波解调方法提取了解析信号，解决了旋转设备中针对非平稳信号的分析问题[3]。

通过上述分析可得，在进行轴承故障诊断之前,将信号进行平稳化处理，然后进行特征提取，最后将提取的特征输入到分类器中进行诊断识别，平稳化处理的过程对于提高轴承识别率是有效的。

近年来，深度学习（deep learning，DL）方法，特别是卷积神经网络（convolutional neural network，CNN）已被应用于原始振动信号的特征提取和自适应分类，其强大的非线性映射能力可以更好地解决基于信号处理的机器故障诊断问题[4-5]。Jia M 等人提出了一种基于“端到端”一维CNN 的故障诊断算法，并在电机轴承数据上进行验证[6]。Li T F 等人在标准CNN 网络中引入连续小波卷积层，提取物理意义明确的高维特征用于故障诊断[7]。Chen Y等人提出了一种新的网络模型ACDIN，将电机轴承故障诊断的准确率从75%提高到95%[8]。Wang L H 等人提出了一种新的基于CNN 和短时傅里叶变换的电机故障诊断方法，能够更加智能、准确地完成电机轴承故障诊断[9]。

但是基于DL 的故障诊断模型只有在训练数据和测试数据的特征分布相似时才能取得较好的诊断效果[10]。实际应用中，由于轴承的转速、载荷等实际工况往往不同，使得振动信号具有不同的特征分布，因此当在一种工况下训练出来的故障诊断模型应用到另一种工况时，诊断准确率会迅速下降。因此，如何最大限度地减小数据之间的分布，将已知工况的知识转移到未知工况是研究的热点和难点。

领域自适应（domain adaptation，DA）作为迁移学习（transfer learning，TL）的一个子方向，在解决数据分布差异问题方面很有成效，其中基于特征的迁移学习是通过变换矩阵将训练数据和测试数据映射到特征空间，进一步减小两个域的分布差异。熊隽等针对不同工况下数据存在分布差异的问题，通过迁移适配，最小化分布差异，从而实现故障的特征迁移适配，最后通过实验证明，该方法结合深度网络有较高的诊断率[11]。

DA 方法中的迁移成分分析（transfer component analysis，TCA）通过减小两个域之间的边缘分布来达到迁移学习的目的，段礼祥等通过TCA 方法将源域和目标域映射到特征空间，成功地减小了变工况条件下两域之间的边缘分布差异[12]。但是对于在不同工况下的轴承数据，除了边缘分布，条件分布通常也不相同。刘应东等将联合分布自适应（joint distribution adaptation，JDA）和KNN 分类算法相结合，通过JDA 方法同时减小了源域和目标域的边缘分布和条件分布差异，实验表明在变工况条件下轴承诊断精度明显提高[13]。但是JDA 方法中的边缘分布和条件分布被赋予了相等的权重，在实际应用中，两者的权重不同，因此在轴承故障诊断中性能有限。王超针对变负载下轴承数据分布差异大的问题，提出了采用平衡分布自适应（balanced distribution adaptation，BDA）将两域之间的数据进行适配，然后构建模型，实验证实了所提方法是有效的，并且准确率较高[14]。

综上所述，针对变工况下的非平稳信号，可以通过角域重采样方法进行平稳化处理，然后通过领域自适应方法，进行适配来减小变工况问题引起的分布差异。因此本文提出了变工况下基于角域重采样的宽度迁移学习（angular domain resampling broad transfer learning，ADR-BTL）方法，先对信号进行平稳化处理，然后结合迁移学习和宽度学习对轴承故障进行诊断，贡献如下：

（1）针对变转速工况下采集到的非平稳信号，通过角域重采样进行平稳化处理，再结合时域、频域、时频域分析方法对轴承故障特征进行提取，构建多域轴承故障特征集。

（2）通过平衡分布自适应方法解决了源域和目标域存在数据分布差异的问题，为轴承故障诊断提供基础。

1 相关工作

1.1 振动信号的平稳化处理

由于变负载、变速等影响，轴承会处于变工况等工作环境，在这种影响下，采集到的振动信号通常是非线性、非平稳信号。阶比分析可以处理非平稳信号，通过角域重采样将非平稳信号转换为平稳信号，然后进行特征提取。本文采用的是基于瞬时频率的估计转速的阶次分析方法，过程如下。

（1）根据希尔伯特变换计算离散的瞬时频率估计。

给定任意的信号x(t)，希尔伯特变换H[x(t)]定义为

将信号x(t)作为实部，作为虚部构成信号z(t)，即：

（2）对瞬时频率的离散数据进行曲线拟合，获得转速曲线。

通过求偏导进一步求解式中的ak，得到多项式：

以上为离散数据进行多项式拟合的步骤，对离散的瞬时频率进行多项式拟合则可以得到转速曲线。为了更好地提高转速拟合的精度，本文通过三阶多项式拟合来获取不同时间段内的转速曲线，p=3，公式如下：

式中：fk(t)为第k段曲线的表达式；a3k、a2k、a1k和a0k为分段拟合得到的多项式系数；t为信号采样的时间。

（3）计算等角度重采样的键相指标。

设等角度采样的时刻为Tn，fi(t)为瞬时频率，则拟合的转速曲线与等角度采样的时刻的关系为

式中：n为采样时刻的序号；Tn为键相指标；T0为拟合曲线的初始时间。

等角度重采样的键相指标θn为

式中：Omax为最大分析阶次，应为采样阶次的一半。

（4）根据求得的θn，利用拉格朗日线性插值定理计算θn处对应的幅值，进一步求出重采样信号。

式中：x(θn)为角域重采样的信号。

1.2 平衡分布自适应

迁移学习主要是通过学习源域带标签数据的特征，实现目标域的识别，对源域和目标域进行领域适配时，如果对边缘分布和条件分布一视同仁，或者只注重某个分布，则适配后的效果可能会变差。Wang J 等人提出的BDA 方法[15]能够根据特定的数据领域，自适应地调整分布适配过程中边缘分布和条件分布的重要性，即通过采用平衡因子μ来动态调整分布之间的距离，实现不同的迁移诊断。

上述为BDA 方法通过μ值动态调整边缘分布和条件分布的距离，μ值不同时，表明服从不同的分布，μ的取值范围是[0,1]，当μ趋近于0 时，表明边缘分布占权重较大；当μ趋近于1 时，此时更注重条件分布。

1.2.1 平衡因子μ的计算

A-distance 是区分两域之间误差的线性分类器（即二分类）,可以通过A-distance 方法来获得μ，用dA来表示A-distance。

1.3 宽度学习

Chen C L P 等提出的宽度学习（broad learning，BL）[16]首先将输入数据转化为特征节点，再将特征节点转换为增强节点，然后将两者的输出连接到输出层，最后构建模型，进行分类。

BL 的具体构造过程如下：

（1）将输入数据Xp通过线性变换，映射生成特征节点Zi。

（2）将特征节点Zi进行非线性变换，生成增强节点Hj。

（3）将增强节点和特征节点组合共同连接到输出层构建网络模型。

式中：C为对角矩阵，是为了保证监督学习部分只使用带标签的数据。

2 基于角域重采样的宽度迁移学习轴承故障诊断

本文提出了ADR-BTL 算法，先将振动信号进行平稳化处理，然后进行领域适配，最后构建宽度学习模型。图1 所示为ADR-BTL 算法的流程图。

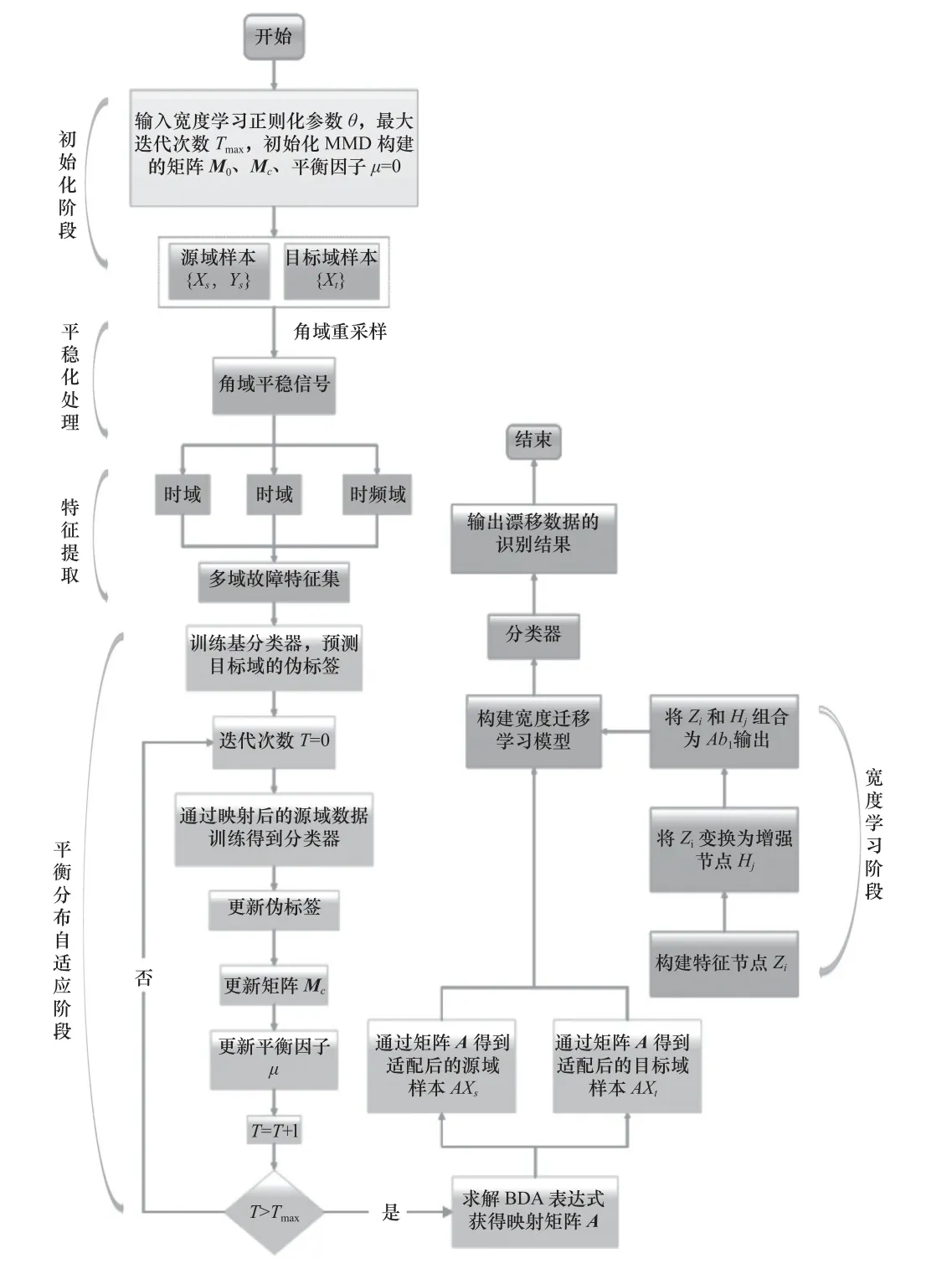
图1 ADR-BTL 算法流程图

以下是ADR-BTL 算法的步骤。

（1）数据平稳化处理过程。

①对信号进行瞬时频率估计。

②对瞬时频率进行曲线拟合，获得转速曲线。

③计算等角度重采样的键相指标。

④根据求得的键相指标，对信号进行插值计算获得角域的重采样信号。

变工况下的非平稳信号经过角域重采样之后，转换为了平稳信号，然后进行多域特征提取，将提取的轴承故障特征集，通过BDA 方法进行适配。

（2）迁移学习过程。

①BDA 首先将源域和目标域映射到特征空间，用最大均值差异（maximum mean discrepancy，MMD）来评估分布差异，因此，式（10）进一步可写为

为了实现类和类之间的迁移，需要计算类内之间的MMD距离，因此通过源域样本训练1 个基分类器，预测目标域的伪标签。

②通过核方法化简得到最终的优化目标：

式中：λ为正则化项的系数；I为单位矩阵；K为中心矩阵；X为由xs和xt共同组成的输入数据矩阵。

MMD构建的M0和Mc矩阵如下：

求解式（24），得到最优变换矩阵A。

③通过矩阵A求得适配后的源域样本ATxs，然后利用{ATxs，ys}进行训练得到分类器f，更新伪标签，逐渐得到精确的伪标签，提升迁移效果。

（3）构建宽度迁移学习模型。

BDA 方法领域适配之后，构建宽度学习模型。首先生成特征节点Zi，进一步转换为增强节点Hj，将Zi和Hj组合输出，得到最终的目标函数：

以下总结了ADR-BTL 算法：

3 实验与分析

实验环境为：Windows10 64 位操作系统，主频2.9GHz 的Intel Core i7-7 500 CPU、8.0GB 内存，编程语言及版本为Matlab R2019b。

3.1 变工况实验数据与设置

采用加拿大渥太华大学的变速轴承振动数据，实验装置如图2 所示，轴通过交流电机驱动，转速通过交流驱动器控制，有2 个ER16K 型轴承来支撑轴，左侧为正常轴承，右侧轴承能够使用不同故障状态的轴承来替代进行实验。传感器用于采集振动信号。

图2 实验装置

该实验共有36 个数据集，其中每个数据集包含了两部分，分别是由加速度传感器测量的振动信号和编码器测量的转速数据。实验中的每个数据集有两种实验设置：变速状况和轴承健康状况，健康状况包括健康状态、内圈故障、外圈故障。工作中的转速条件为升速、降速、先升后降、先降后升，振动信号的采样频率为200 kHz，采样时长为10 s。

3.2 基于角域重采样的实验数据分析

3.2.1 时域振动信号与转速脉冲信号

在变转速工况下，采集到的时域振动信号如图3所示，此时振动信号的特点为非线性、非平稳，如果用于轴承故障诊断，可能导致训练的模型识别率大幅度降低。因此，本文通过角域重采样方法对非平稳信号进行分析，实现对非平稳信号的平稳化处理。

图3 采集的时域振动信号图

3.2.2 角域重采样

重采样过程中，转速和时间的关系如图4 所示。通过重采样得到的角域振动信号如图5 所示。

图4 转速和时间的关系

图5 角域振动信号图

3.2.3 特征提取

将振动信号进行平稳化处理之后，将其进行特征提取，包括14 个时域特征、5 个频域特征、8 个时频域特征构建多特征数据集，图6 所示为提取的时域特征，图7 所示为提取的频域特征，图8 所示为变分模态分解得到的前8 个分量。

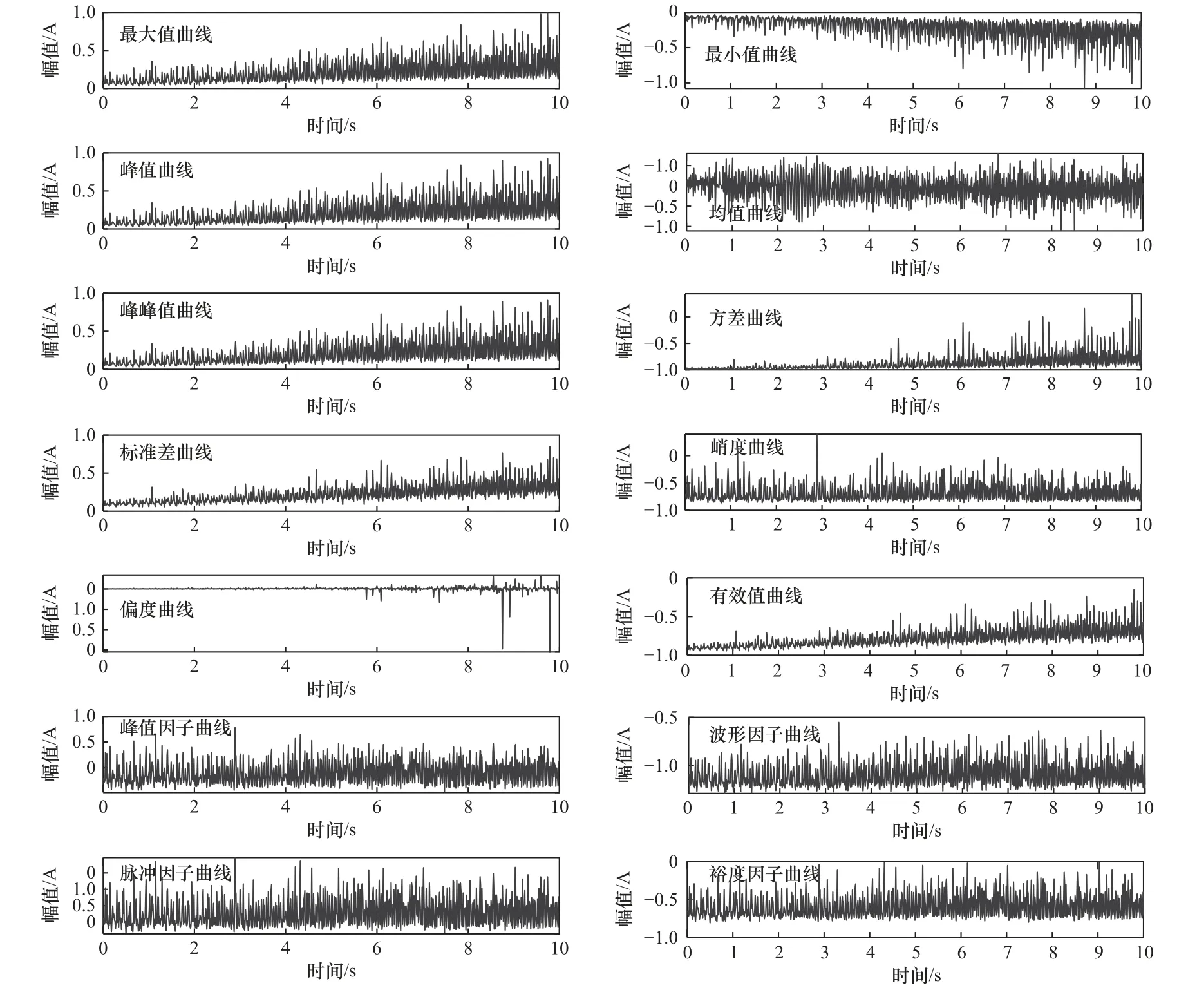
图6 时域特征提取图1-14

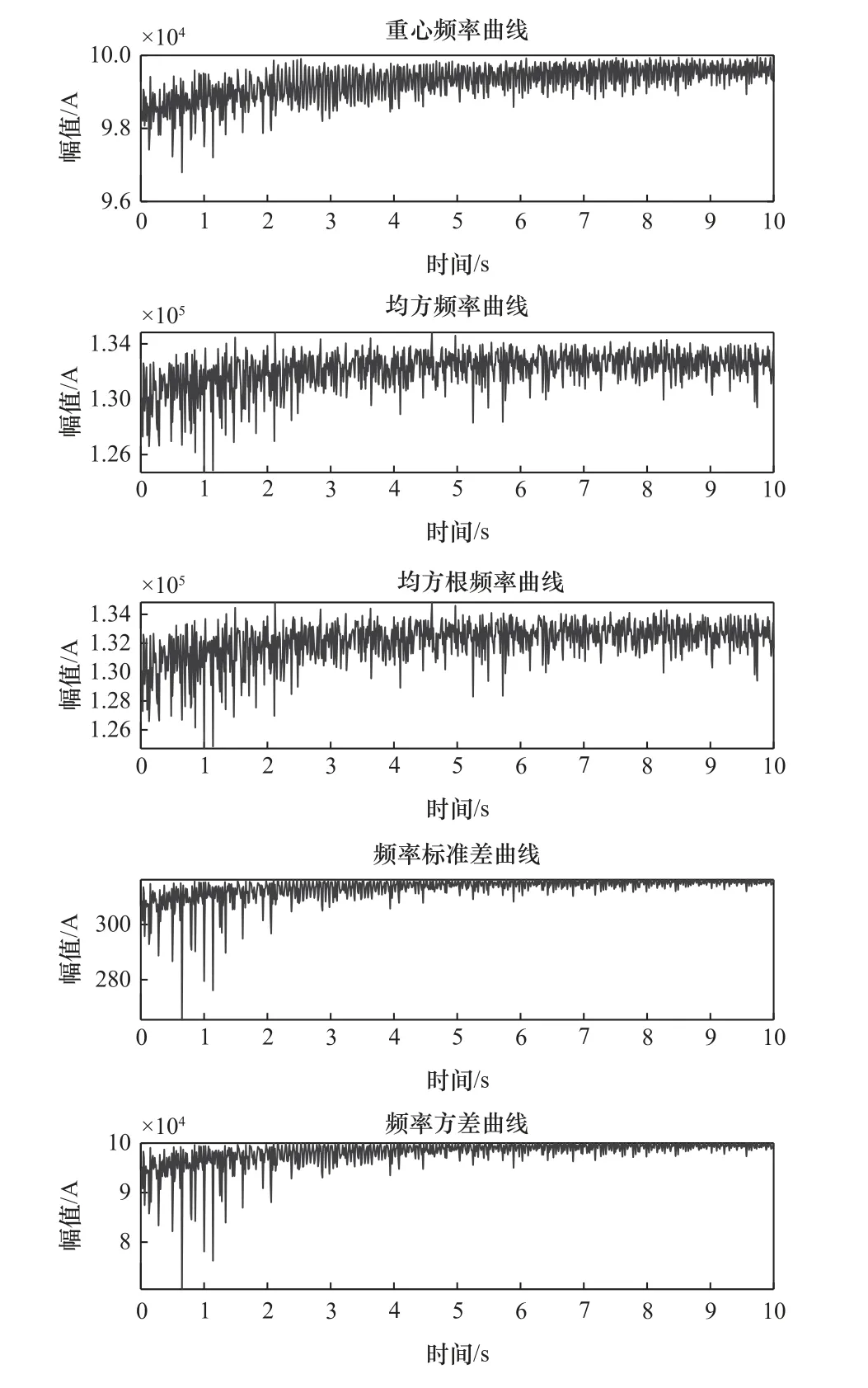
图7 频域特征提取图

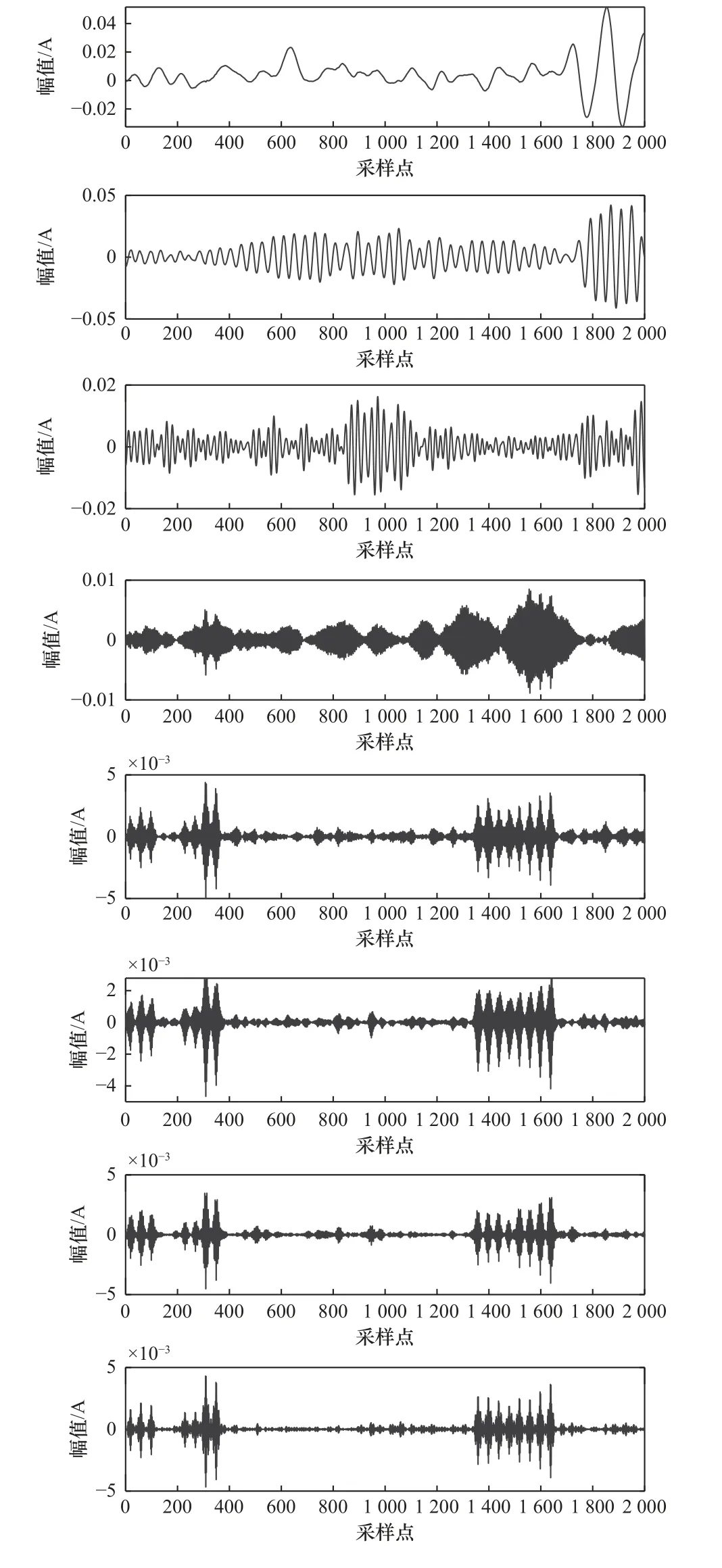
图8 VMD 分解的前8 个分量

4 迁移学习仿真样本分析

本节通过仿真样本来模拟源域和目标域经过迁移学习之后的适配效果，进一步验证领域自适应方法中BDA 的适用性。

通过Matlab 软件随机产生四组满足正态分布的二维数组，模拟在变工况条件下有两种轴承故障类别的源域和目标域样本，仿真样本的散点如图9 所示。图10 所示为仿真样本的概率密度曲线，表示两域之间的样本分布情况。

图9 仿真样本散点图

图10 仿真样本概率密度曲线图

生成仿真样本之后，通过BDA 方法进行适配来拉近两域样本的分布距离，然后给出适配之后的样本散点图和概率密度曲线图，如图11 所示。

图11 适配后的散点图和概率密度曲线图

通过图11 可得，适配之后的散点图中，源域和目标域数据距离明显减小，适配之后的曲线重叠率明显提高，表明变工况条件下，源域和目标域经过BDA 方法之后，数据分布差异明显减小，BDA方法可以有效地提高域间的分布一致性。

5 实验性能对比

将本文提出的ADR-BTL 算法与以下应用于轴承故障诊断的算法进行比较：

（1）小波包分解-宽度学习（wavelet broad learning，WBL）[17]。

（2）角域重采样-核极限学习机（angular domain resampling-kernel based extreme learning machine，ADR-KELM）[18]。

（3）角域重采样-一维卷积神经网络（angular domain resampling-1D convolutional neural network,ADR -1DCNN）[18]。

（4）宽度迁移学习（broad transfer learning,BTL）[14]。

ADR-BTL 相关的随机参数Wei、βei、Whm、βhm来自区间[-1,1]上的标准均匀分布，对于增强节点的生成，选择sigmoid 函数作为激活函数。ADRBTL 的初始化结构为10 × 100 个特征节点和2 000个增强节点。ADR-BTL 中涉及2 个可调参数。设置θ=0.01，λ=0.2，由于ADR-BTL 中存在随机权值，因此对每组参数运行10 次。

提出的算法ADR-BTL 与对比算法数据分析见表1。

表1 方法识别率对比

为了可视化结果，在图12 中绘制了与表1 对应的折线图。

图12 识别准确率曲线

由表1 和图12 可以得出以下结论:

（1）ADR-KELM 和ADR-1DCNN 的轴承故障识别率优于WBL，表明角域重采样可以提高模型的性能。

（2）BTL 的模型识别率优于ADR-KELM 和ADR-1DCNN，表明迁移学习可以减小数据分布差异，有效提高模型识别率。

（3）ADR-BTL 的性能优于BTL，表明本文提出的方法中，角域重采样结合迁移学习对提高宽度学习模型的性能是有效的。

6 结语

本文提出了用于轴承故障诊断的算法ADR-BTL。

首先通过角域重采样将非平稳信号转换为平稳信号，提取了14 个时域特征、5 个频域特征、8 个时频域特征构建多域特征数据集，然后通过BDA进行领域适配来解决变工况下样本的分布差异问题，最后构建宽度迁移学习分类模型。

通过仿真数据表明BDA 方法拉近了域间的距离，即有效地减小了分布差异，通过实验数据验证了角域重采样方法可以对振动信号进行平稳化处理，最后通过实验数据对比分析，证实了本文提出的ADR-BTL 算法优于其他对比的算法，识别性能是最好的。

在接下来的工作中，可以考虑模型的鲁棒性，继续进行改进。