基于正演模拟的巨厚低阻盖层影响分析

章 惠，隋少强，张 慧，魏广仁，刘晓红

（1.中国石化集团新星石油有限责任公司，北京 100083；2.中国石化地热资源开发利用重点实验室，北京 100083；3.华北水利水电大学 地球科学与工程学院，郑州 450000）

山东省齐河县桃园社区位于鲁中隆起地热田，拥有丰富的地热资源，具有良好的地热开发利用前景。齐河县地热资源主要赋存于奥陶系-寒武系碳酸岩岩溶-裂隙中[1-2]，为进一步查明热储分布，桃园社区前期布置了4 条可控音频源大地电磁（CSAMT）剖面和大地电磁（MT）剖面[3]。根据预测结果推断热储上覆有约1 000 m 的第四系及新近系沉积地层，且电测结果表明，沉积地层的电阻率为2-10Ω·M。巨厚的低阻盖层对中高频电磁信号有着强衰减作用，造成实际有效勘探深度变浅，影响了深部断裂构造的探测能力，导致钻井误差加大，给当地的新能源开发工作带来极大的经济损失。因此，亟需了解齐河桃园地区巨厚低阻层对深部热储和断裂构造识别精度的影响，从而更好地预测热储发育情况，提高钻井成功率。

本文以齐河桃园地区实际电性参数为依据，从多解性较强的断裂构造入手，通过开展大地电磁正演模拟，研究不同盖层变量和热储变量对深层断裂热储的影响，总结归纳了巨厚低阻层下断裂热储的频率-电阻率相应特点，为指导本地区的电磁方法采集工作和地质解释工作提供有利信息。

1 大地电磁正演模拟理论基础

电磁波在地下介质中的传播满足麦克斯韦方程组，大地电磁正演模拟方程的推导也需要从麦克斯韦方程出发。在二维介质中，电磁场能分成独立的两组波型，一组包括电磁场分量Ex、Hy、Hz，称为TE 极化模式；一组包括电磁场分量Hx、Ey、Ez，称为TM 极化模式。在求二维介质中大地电磁场的数值解时，麦克斯韦方程组的求解问题可转化为以下Ex、Hx满足的二阶偏微分方程的求解问题[4-5]

式中：Ex为x 方向的电场水平分量，Hx为x 方向的磁场水平分量，σ 为介质电导率，ε 为介质的介电常数，μ为介质的磁导率，ω=2πf 为圆频率。为了求解式（1）、（2），需要给出其边界条件。

以TM 模式为例，令u=Hx，τ=σ-iωε，λ=iωμ。对于TM 极化模式，上边界AB 直接取在地面上，并以该处的场值u 为1 单位，则有

下边界CD 以下为足够深度的均质岩石，局部不均匀体产生的异常场在CD 上为零，此时电磁波在下边界以下的传播方程为

式中：u0为常数为传播系数，σ 为岩石电导率。对式（4）求导，得而在下边界处因此下边界CD 的边界条件为

当地质模型的左右边界离局部不均匀体足够远时，不均匀体的异常场在左右边界上为零，电磁场在左右边界上对称，其边界条件为

综合以上分析，求解大地电磁场总结为偏微分方程式（1）、（2）及边值条件式（3）—（6）组成的方程组（7）的求解问题

采用有限单元法计算方程组（7）的数值解，考虑其变分问题，方程组（7）与下列变分问题等价

有限差分分析法中，采用矩形网格将整个模型区域Ω 剖分成有限个矩形单元，利用双二次插值对矩形单元进行插值，在每个小矩形单元上对式（8）进行积分，然后对各单元求和[5]。计算出各节点的场值u 后，再利用数值方法求出场值沿垂向的偏导数TM 极化模式下即代入到式（8）中即得到视电阻率和阻抗相位。

TE 极化模式下有

式中：Zxy为TE 极化模式下的阻抗，ρxy为TE 极化模式下的视电阻率，φxy为TE 极化模式下的相位。

TM 极化模式下有

式中：Zyx为TM 极化模式下的阻抗，ρyx为TM 极化模式下的视电阻率，φyx为TM 极化模式下的相位。

2 巨厚低阻盖层对断裂构造识别的影响

基于齐河桃园地区区域构造及地层电性参数，建立盖层为巨厚低阻层的简单断裂热储模型（图1）。从上至下依次为：①第四纪-新近纪（Q-N）低阻盖层，厚度1 000 m，电阻率为10 Ω·m；②石炭－二叠纪（C-P）地层，厚度200~1 000 m，电阻率为100 Ω·m；③奥陶纪（O）地层，厚度800 m，地层电阻率1 000 Ω·m；④基底，电阻率为5 000 Ω·m。为了更好地分析巨厚低阻盖层对断裂构造识别的影响，对模型分以下3 种情况进行正演模拟：①固定盖层的厚度和电阻率值，改变断裂带的电阻率；②固定盖层和断裂带的电阻率，改变盖层的厚度；③固定盖层的厚度和断裂带电阻率，改变盖层的电阻率。

图1 盖层为巨厚低阻层的断裂热储模型

所有模型正演模拟周期为10-2~103s，频率采样点数61，等对数间隔采样。

2.1 断裂带电阻率为变量

以巨厚低阻层下的断裂构造识别能力为研究目标，当低阻层厚度为1 000 m，电阻率为10 Ω·m，改变断裂带电阻率得到的频率-电阻率曲线。

图2 为模型断裂带电阻率为变量时得到的A 测点ρxy视电阻率响应曲线。从图中看出，视电阻率曲线对盖层的反映为平直线。随着频率降低（约小于2 Hz），视电阻率曲线呈现线性上升趋势，地层视电阻率分布表现为由浅至深增加，断裂热储层的低阻特征没有体现。且当ρf变化范围为10~100 Ω·m 时，不同模型的视电阻率响应曲线几乎重合。表明穿透1000m 厚的低阻（10Ω·m）盖层的电磁波对断裂热储分辨率非常低，单测点视电阻率曲线无法体现其异常特征。当ρf=2 Ω·m 时，其平直段更长，具有一定的对断裂热储层的分辨能力。

图2 模型断裂带电阻率为变量时得到的ρxy 视电阻率响应曲线

图3 为模型断裂带电阻率为变量时得到的ρxy视电阻率正演模拟剖面。当ρf变化范围为10~100 Ω·m时，ρxy视电阻率剖面基本接近于平层模型的响应，视电阻率等值线平直、连续。

图3 断裂带电阻率为变量时ρxy 视电阻率正演模拟剖面

当ρf=2 Ω·m 时，ρxy视电阻率剖面中断裂热储发育对应的位置等值线出现明显的下凹增厚，呈“U”形。这说明在1 000 m 厚10 Ω·m 的巨厚低阻盖层影响下，大地电磁方法对埋深1 200 m 以下的断裂热储分辨能力非常低，只有当热储层富水、破碎强烈，从而与围岩电阻率相差大的情况下（如ρf=2 Ω·m）才可能对热储有所反映。

2.2 盖层厚度为变量

分析盖层电阻率等其他参数固定时，改变盖层厚度得到的频率-电阻率曲线。设置模型低阻层电阻率为10 Ω·m，断裂带电阻率为10 Ω·m，改变低阻层厚度得到的频率-电阻率曲线。

图4 是盖层厚度为变量时得到的A 测点视电阻率响应曲线。当盖层厚度为100 m 时，ρxy曲线在4 Hz、1 Hz 频点处出现拐点，反映中间地层电阻率变低。当盖层厚度大于150 m 时，根据趋肤深度理论，电磁波会直接穿过盖层到达中间层，对盖层低阻特征无反映。

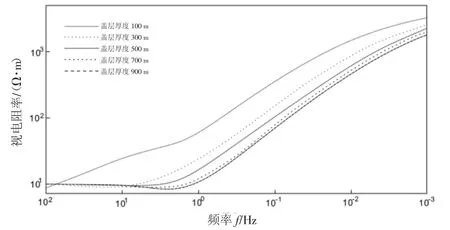
图4 盖层厚度为变量时得到的ρxy 视电阻率响应曲线

图5 为盖层厚度为变量时得到的ρxy视电阻率正演模拟剖面。从图中看出，当盖层厚度为100 m、300 m时，ρxy视电阻率剖面中，对应断裂热储发育的位置处等值线呈现下凹增厚的现象，显示局部存在低阻构造；当盖层厚度大于300 m 时，ρxy视电阻率响应类似于平层反射，等值线沿横向无变化。

图5 盖层厚度为变量时ρxy 视电阻率正演模拟剖面

2.3 盖层电阻率为变量

分析盖层厚度等参数固定时，改变盖层电阻率得到的频率-电阻率曲线。设置模型低阻层厚度为1 000 m，断裂带电阻率为10 Ω·m，改变低阻层电阻率得到的频率-电阻率曲线。

图6 为盖层电阻率为变量时得到的ρxy视电阻率正演模拟剖面。从图中看出，当盖层电阻率为10 Ω·m时，ρxy视电阻率等值线表现为平直线，无异常特征。在断裂热储发育的位置，当盖层电阻率为30 Ω·m 时，ρxy视电阻率等值线局部增厚呈“U”形异常，当盖层电阻率增加（50~100 Ω·m）时，ρxy视电阻率等值线出现下凹的低阻带，对断裂及热储引起的异常均有反映。

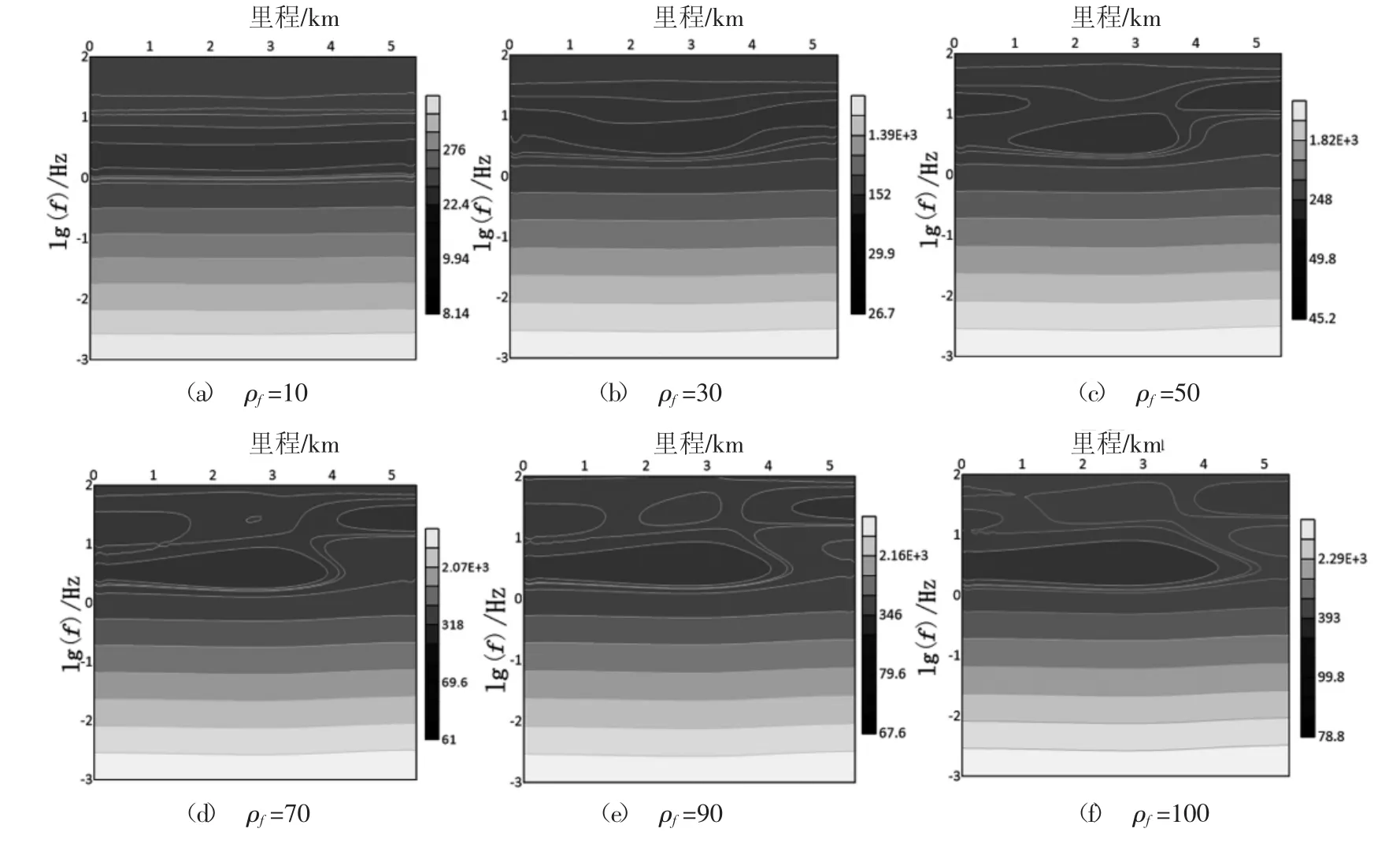
图6 盖层电阻率为变量时ρxy 视电阻率正演模拟剖面

3 结论

本文通过对齐河桃园地区巨厚低阻盖层模型的正演模拟，分析了巨厚低阻层对深层断裂热储构造的影响，正演模拟结果显示：

1）在大地电磁测深中，由于巨厚低阻层对中、高频电磁波的强烈衰减，严重影响了大地电磁测深的有效深度。在厚度1 000 m、电阻率10 Ω·m 的盖层影响下，大地电磁测深方法对深层断裂热储几乎无法识别，只有当断裂热储电阻率极小时（如2 Ω·m）且与围岩电阻率相差大的情况下，TE 模式下的视电阻率才可能对热储有微弱响应。

2）以盖层厚度为变量的正演模拟结果显示，基于齐河桃园地区地下电性结构分布，当低阻盖层厚度小于300 m 时，断裂热储发育的位置处视电阻率等值线才会出现局部下凹增厚（TE 模式）的异常特征，且这一异常响应相对较弱。

3）以盖层电阻率为变量的正演模拟结果显示，对齐河桃园地区埋深1 200 m 以下的断裂热储，影响大地电磁测深成像精度主要为盖层的电阻率。当盖层电阻率增加至40 Ω·m 以上时，TE 模式的视电阻率等值线会出现明显的下凹增厚的异常特征。