基于金豺狼优化算法的数控切削参数优化
赵 飞, 王丽娟, 任善良
(1.晋城职业技术学院 机械与电子工程系,山西 晋城 048000, E-mail: zhaoff1982@126.com;2.郑州升达经贸管理学院 信息工程学院,郑州 451191;3. 驻重庆地区第五军代室,重庆 404000)
随着制造行业对零部件加工质量和节约成本要求的不断提升,实现零部件加工的高精度、高效率和低成本成为各制造企业不断追求的目标[1-3]。然而,现有的数控切削策略大多是技术人员依据传统方式或者历史经验来完成切削参数的给定,在加工质量、成本、效率之间很难做好平衡,因而需要设计出优秀的算法来调控切削参数[4-6]。
随着智能优化算法的发展,不少学者通过智能优化算法来进行数控切削参数的自适应优化,实现了加工质量、效率的提升,且降低了成本[7-10]。该应用的主要思路就是将数控切削参数优化问题,转换为转化为带约束条件的函数优化问题,而后通过智能优化算法进行求解,从而得到最优切削参数。如严胜利等[11]提出的基于改进遗传算法的数控铣削参数优化方法、吴昊等[12]提出的基于离散粒子群算法的复杂曲面微小零件切削参数优化方法、邓宇峰等[13]提出的基于改进人工蜂群算法的数控切削参数优化方法、张克道等提出的基于帝王蝶优化算法的铣削参数优化方法等,都在一定程度上提高了加工效率,或减少了加工成本,或提高了加工质量,展现出了一定的优势。
从目前的研究成果来看,智能优化算法已成为一种有效的数控切削参数优化方法。但上述提到的相关智能优化算法由于算法本身存在一定的缺陷,故在进行切削参数优化时,并不能完全达到满意的结果。同上述提到了一些智能优化算法类似,于2022年金豺狼优化算法[14](Golden Jackal Optimization,GJO)也是一种智能优化算法,具有原理简单、参数设置少、运算速度快等特点,在基准函数测试和机械优化设计实例中展现了优异性能。
本文为提高数控切削参数优化的效果,首次将GJO算法用于数控切削参数优化中,并以复杂曲面且微小滚齿加工为实例,进行了数控切削参数优化的实验验证,结果验证了GJO在参数优化中的有效性。
1 数控切削参数优化建模
1.1 切削参数优化目标函数
对于数控切削参数优化而言而言,其目标提高生产效率、降低生产成本。在切削过程中,主要考虑切削速度、进给量和切削深度这3个参数的设置。其中,切削深度对刀具的磨损影响较切削速度和进给量要相对更小,并且可以根据实际加工情况选择确定。因此,切削速度、进给量的合理确定就显得更为重要。
首先,建立提高生产效率的目标函数,它的表达式为:
T=T1+T2+T3+T4+T5
(1)
式中:T1为工人安装刀具所花费的时间;T2为零部件完成切削所花费的时间;T3为每道工序换刀所花费的平均时间;T4为机床空行程所花费的时间;T5为辅助工作所花费的时间。
(2)
式中:A、B、a分别为刀具头数、模数、转数;C为切出长度;b为切入长度;e为走刀数量;v为切削速度。
(3)
式中:g为刀具耐用度系数;F为刀具磨损的换刀时间;c和G分别为刀具直径、齿数;H为刀具纵向的每齿进给量;d和h分别为切削宽度和切削深度。
其次,建立降低生产成本的目标函数,它的表达式为:
(4)
式中:D1为毛坯成本;D2为单位时间人力成本;D3为单位时间机床损耗成本;D4为刀具成本。
引入一个参数λ,将式(1)和式(4)的目标函数进行加权,得到单一优化目标函数为:
(5)
式中:当λ=1时,则目标函数转换为以提高生产效率为目标;当λ=0时,则目标函数转换为以降低生产成本为目标;当0<λ<1时,则目标函数是提高生产效率和降低生产成本为目标,是二者的一个折中。
1.2 切削参数优化约束条件
机床主轴功率不能超过额定功率,约束条件为:
Iu-JPmax≤0
(6)
式中:I为刀具在主运动方向上的力;u为切削能耗;J为机床运行速率;Pmax为机床最大功率。
为降低机床磨损,施加的切削力应在机床主轴允许范围内,约束条件为:
I-MLmax≤0
(7)
式中:M为进给速度;Lmax为机床主轴最大切削力。
切削参数不能超过机床的有效范围,约束条件为:
(8)
式中:dmin、dmax与hmin、hmax分别为切削宽度和切削深度的上下限;Mmin、Mmax和Nmin、Nmax分别为进给速度和刀具转速的上下限。
刀具每齿进给量,应满足机床进给约束,约束条件为:
(9)
式中:n为待加工工件直径;p为刀具每齿进给量。
加工后零件的表面粗糙度,约束条件为:

(10)
式中:qmax为粗糙度最大值;O为刀尖圆弧半径。
切削扭矩不能超过主轴最大扭矩,约束条件为:

(11)
式中:Zmax为机床主轴最大扭矩。
以上式(6)~(11)为优化约束条件。
2 金豺狼优化算法
GJO是一种模仿金豺狼的合作狩猎行为的新型智能优化算法。在搜索空间中,金豺狼种群初始化数学描述为:
Y0=Ymin+rand×(Ymax-Ymin)
(12)
式中:Yo为金豺狼种群的初始位置;rand为[0,1]范围内的随机数;Ymax和Ymin分别为待求解问题的搜索上边界和下边界。
在GJO算法中,猎物矩阵表示为:
(13)
式中:Yi,j为第i只猎物的在第j维空间中的位置;N为猎物的数量,即金豺狼种群的数量;d为待求解问题的维数。根据建立的适应度函数(目标函数),可得猎物的适应度值矩阵为:
(14)
式中:f(·)为适应度函数(目标函数)。将适应度值最优和次优猎物位置分别赋予雄性豺狼和雌性豺狼,并将二者组成豺狼对。
判定猎物逃脱能量E的大小,当时|E|>1,则金豺狼种群进入搜索猎物阶段(勘探阶段);当|E|≤1时,则金豺狼种群进入攻击猎物(开发阶段)。其中,逃脱能量E的计算公式为:
E=E1*E0
(15)
式中:E1表示猎物逃脱能量逐渐降低的过程;E0表示猎物逃脱能量的初始状态。它们的计算公式分别为:
(16)
式中:t和T分别表示当前迭代次数和最大迭代次数;c1为常数,一般取值为1.5;r为[0,1]范围内的随机数。
对于勘探阶段,金豺狼种群的在豺狼对的指引下,其位置更新方式为:
(17)
对于开发阶段,金豺狼种群的在豺狼对的指引下,其位置更新方式为:
(18)
式(12)和式(13)中:YM(t)和YFM(t)分别表示雄性豺狼和雌性豺狼在第t次迭代开始时的位置;Y1(t)表示在在雄性豺狼指引下得到的金豺狼种群位置;Y2(t)表示在雌性豺狼指引下得到的金豺狼种群位置;Y(t)表示第t次迭代完成后,金豺狼种群的位置;l表示一个基于莱维分布(Levy Distribution)的一个随机数,它的计算方式为:
l=0.05*Levy
(19)
式中:Levy就是莱维分布随机数,它的计算公式为:
Levy=μ/|v|1/β
(20)
式中:β在(0,2)范围内取值,通常取为1.5;μ和v服从式(16)所示的正态分布:
(21)
式中:σμ、σv满足式(17)
(22)
式中:Γ(·)表示伽马函数。
GJO算法的主要流程如图1所示。
3 滚齿加工实例分析
3.1 加工参数
本文通过对具有复杂曲面且微小的滚齿进行加工,来验证所提方法的有效性。加工中心型号为YKS3120A,主轴最大转速为16 000 r/min,电机最大功率为34 kW;滚齿加工毛坯长宽高分别为40 mm、38 mm、21mm,材料为Q235碳素钢,齿数为42;刀具为镶齿盘铣刀,材料为YG6硬质合金,悬长80 mm,刀片数2,刀粒数70,耐用系数0.83,主偏角70°,转位2次。根据工艺方案和相关生成数据,可得加工毛坯成本为28元,刀具成本为220元,单位时间机床磨损和劳动成本分别为2.3 元/min和0.3 元/min。加工过程中机床、工件、工具等具体技术参数如表1至表3所示。
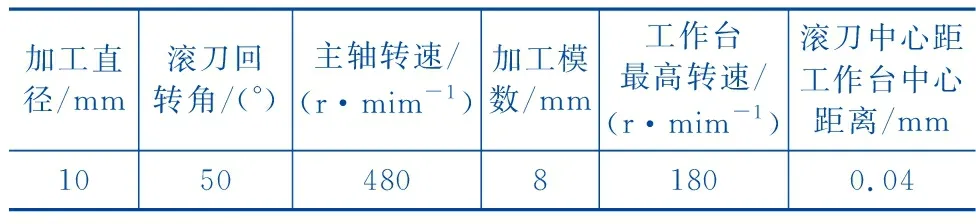
表1 机床参数

表2 刀具参数

表3 工具参数

▲图1 GJO流程图
3.2 加工过程
以表1至表3所示加工技术参数为基本参数,齿轮毛坯采用外圆纵车加工,一次滚齿加工完成,加工余量为0.8 mm。根据实际情况,确定生产效率和生产成本之间的权重系数为0.3,建立参数优化数学模型。其中,切削速度的范围为[0,4],进给量的范围为[0,4],GJO算法的最大迭代次数设置为200,种群规模设置为30。切削深度为1.2 mm/r时,滚齿加工的GJO参数优化过程如图2所示。
从图2中可以看出,在0次迭代时,GJO算法中金豺狼种群是在切削速度和进给量的取值范围内随机分布的,无聚集倾向;在50次迭代时,金豺狼种群出现了一定程度的聚集,切削速度的范围变化为了[0,2],进给量的范围仍是在[0,4];在100次迭代时,金豺狼种群实现了较大程度的聚集,切削速度的范围变化为了[0,1],进给量的范围变化为了[2.5,4];当迭代次数为150时,金豺狼种群几乎汇聚到了一起,基本快要寻找到最优解,随着迭代次数的再增加,当种群汇聚一点时,即可得到切削速度和进给量的最优解。
3.3 结果分析
为了验证GJO算法的优势,将其与改进遗传算法[11](IGA)、离散粒子群算法[12](DPSO)、改进人工蜂群算法[14](IABC)等方法进行对比。上述4种方法中,种群规模均设置为30,最大迭代次数设置为200,IGA、DPSO和IABC这3种方法所需要的其余参数均按原文献进行设置。在不同切削深度下,上述4种方法所得切削速度和进给量的最优解如表4所示。利用表4所示不同切削深度下4种方法所得最优切削参数分别进行连续20个滚齿毛坯加工,记录每个滚齿加工总工时,得到滚齿成品后,对每个滚齿表面粗糙度进行测量。4种方法在不同切削深度下加工总时间对比如图3所示、表面粗糙度对比如图4所示。

表4 各方法切削参数优化结果

▲图2 切削参数的GJO优化过程
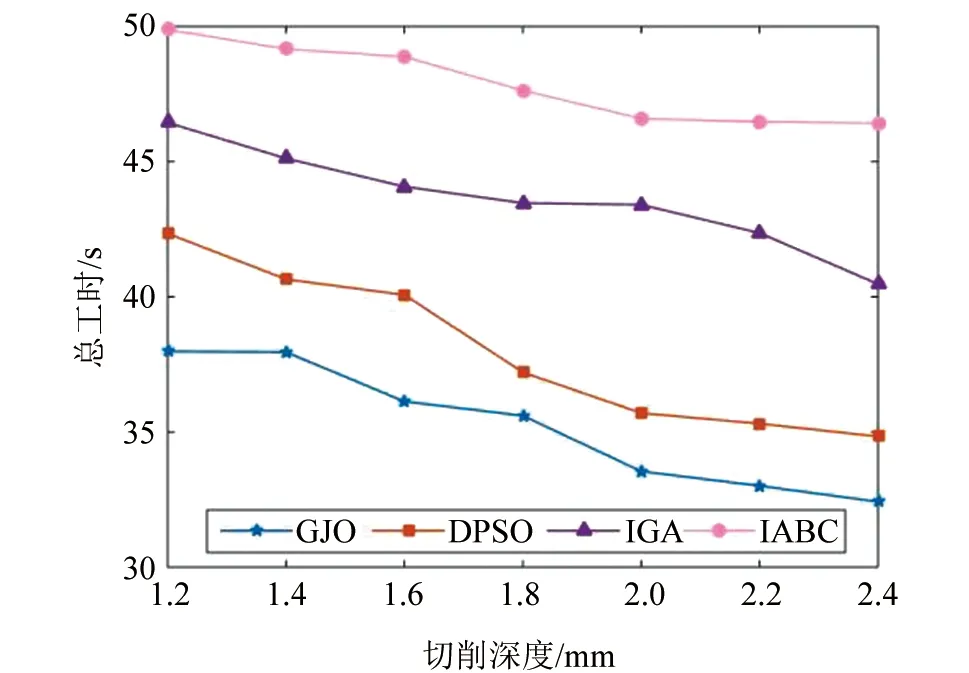
▲图3 滚齿加工总时间对比结果

▲图4 滚齿表面粗糙度对比结果
从图3中可以看出,随着切削深度的增加,加工总工时呈现出下降趋势,但不管在哪一种切削深度下,4种方法中均是本文提出的GJO的加工总工时最少。同时,经计算,几种切削深度的平均总工时,GJO为35.23 s,较IGA的43.62 s、DPSO的38.02 s和IABC的47.86 s,分别缩短了6.11 s、8.39 s、2.78 s和12.64 s,分别缩短约20%、8%和29%,加工效率得到了明显提升。
对于该批滚齿,要求其表面粗糙度需小于0.7 μm,从图4中可以看出,所有滚齿成品表面粗糙度均满足要求,且随着切削深度的增加,粗糙度呈上升趋势,但不管在哪一种切削深度下,本文所提GJO方法的粗糙度均是4种方法中最小的。同时,经计算,几种切削深度的平均粗糙度,GJO为0.33 μm,较IGA的0.45 μm、DPSO的0.37 μm和IABC的0.48 μm,分别降低了0.12 μm、0.04 μm和0.15 μm,加工质量得到了有效提升。
4 结论
为提高数控切削参数优化效果,提出了用于切削参数优化的GJO算法。通过复杂曲面微小滚齿加工实例对方法的有效性进行了验证,并与其余4种方法进行了对比分析。结果表明,所提方法的滚齿加工总工时缩短约8%~29%、表面粗糙度降低了0.04 μm~0.15 μm,加工效率和质量均得到提升。

