基于AO-VMD-BiGRU的短期负荷预测方法

汝洪芳,张程帝,王国新,李作淘

(黑龙江科技大学 电气与控制工程学院,哈尔滨 150022 )

0 引 言

在双碳背景下,新能源发电比例逐年提升,同时,也给电网的稳定性带来了极大的挑战。若是能够对短期电力负荷进行精准的预测,这不仅能够促使供电企业制定更加周密的发电计划,优化电力调度规划,还能保证电力系统的安全,符合绿色发展的要求。

从文献资料上看,一些成熟的预测短期负荷的方法主要有自回归移动平均法(autoregressive integrated moving average, ARIMA)[1-2]、卡尔曼滤波法[3]等方法。上述几种方法均可以对各个影响因素进行捕捉,并确定各因素之间的线性关系,但也存在明显的不足,那就是无法对非线性特征进行描述。常用的深度学习短期负荷预测方法有以下几种:反馈神经网络(back propagation,BP)[4]、卷积神经网络(convolutional neural network,CNN)[5]、循环神经网络(recurrent neural network,RNN)[6]等模型的预测方法。文献[7]采用门控循环单元(gate recurrent unit,GRU)对电力负荷进行预测,与长短期记忆网络(long short-term memory,LSTM)相比,更易于计算,但是负荷预测是由历史时刻信息和未来时刻信息共同决定,GRU没有对未来时刻信息进行考虑。文献[8] 采用经验模态分解(empirical mode decomposition,EMD),借助此方法完成电力负荷的分解工作,降低了负荷预测的复杂性,但此种分解模态容易出现模态混叠的情况,这非常影响负荷预测的精度。文献[9]采用变分模态分解(variational mode decomposition,VMD)对电力负荷进行分解,取得很好的实验效果,但是人为设置参数具有很强的随机性,影响其分解性能。

为了提高短期负荷预测精度,本文提出一种基于天鹰算法(aquila optimizer,AO)优化变分模态分解和双向门控循环单元(bidirectional gate recurrent unit,BiGRU)神经网络的短期电力负荷预测方法。首先,利用VMD取代EMD,对负荷序列进行分解,得到电力负荷分解序列图像,解决EMD本身的模态混叠缺点;其次,采用AO取代人为设置,对VMD参数进行选择,降低了试验的随机性;最后把分解后的负荷序列传递到双向门控循环单元中进行数据的非线性拟合,在澳大利亚昆士兰地区负荷数据基础上进行短期负荷预测。将该方法与BiGRU神经网络模型、VMD-BiGRU神经网络模型、WOA-VMD-BiGRU模型进行比较,来验证所提方法的准确性。

1 AO-VMD-BiGRU模型原理

1.1 AO

天鹰优化算法是2021年Laith Abualigah等人提出的一种新型智能优化算法[10],该算法主要模拟天鹰在捕捉猎物过程中的自然行为,来达到寻优的目的,具有寻优能力强、收敛速度快等特点。

1.2 VMD

变分模态分解,即VMD,此方法是Dragomiretskiy等人在2014年提出的[11],此种信号分解方法具有一定的自适应性。此模型借助迭代搜索变分方法最优解,从而精准确定各个分量的中心频率以及宽带,同时彻底克服了EMD方法的诸多弊端,比如端点效应、模态分量混叠等难题。VMD算法的约束公式如下:

(1)

(2)

式中:{uk}为模态分量的集合;{wk}为各模态分量的中心频率;*为卷积运算;∂t为函数对时间的导数;δ(t)为单位脉冲函数;f(t)为原始输入信号。

把拉格朗日因子代入约束公式,从而将其转换为非约束的变分问题,如下:

L({uk},{wk},λ)=

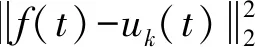
(3)

式中:α为惩罚因子;λ为拉格朗日因子。

模态分子变量和中心频率的更新公式如下:

(4)

(5)

式中:f(w)、ui(w)、λ(w)分别为f(t)、ui(t)、λ(t)的傅里叶变换;n为迭代次数。

1.3 BiGRU模型

BiGRU模型是在2个方向相反GRU模型的基础上搭建的神经网络结构,GRU网络模型如图1所示。这2个GRU网络模型都能接收到相同的输入,所以该模型在处理时间序列数据上有优势,负荷预测的准确率提高[12]。选择BiGRU网络模型,如图2所示。

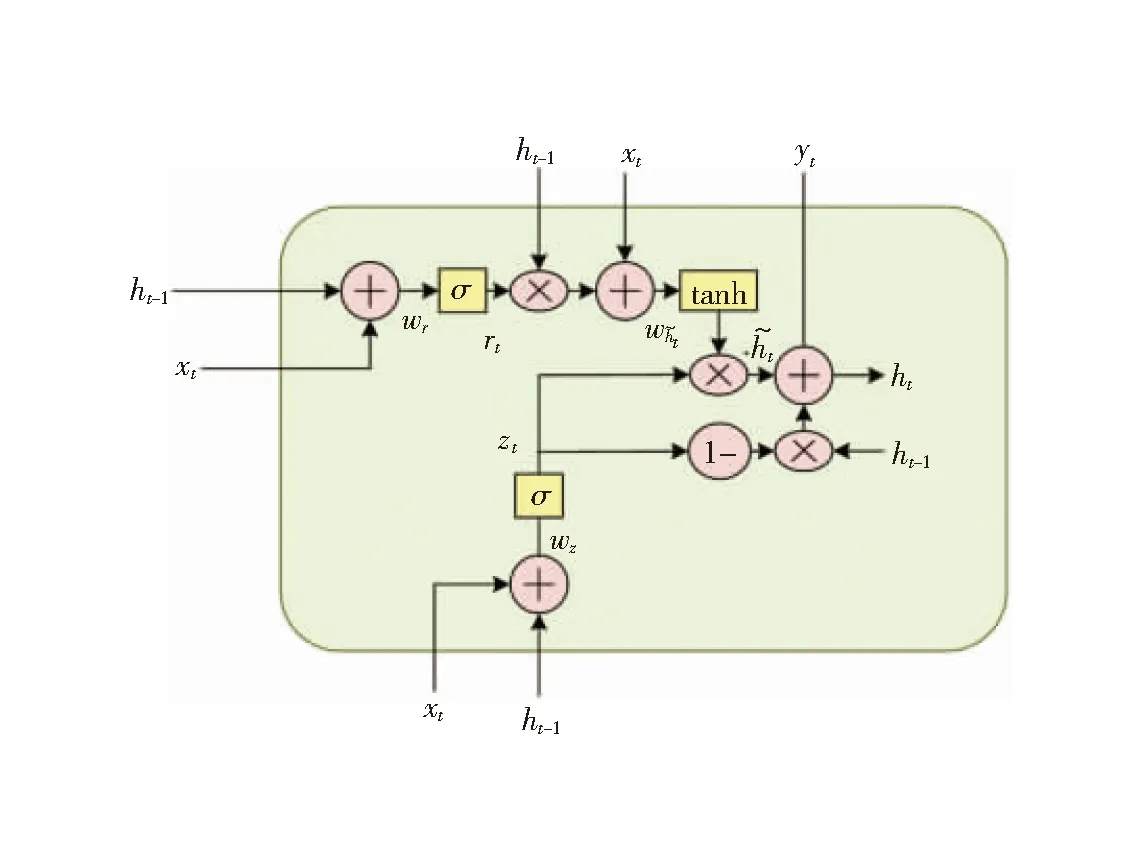
图1 GRU原理图

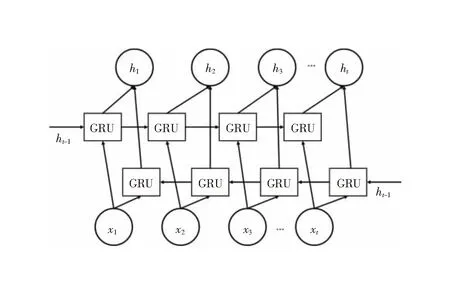
图2 BiGRU原理图

GRU网络公式如下:

rt=σ(wr[ht-1,xt])

(6)

zt=σ(wz[mt-1,xt])

(7)

(8)

(9)

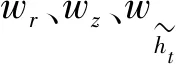
BIGRU网络公式如下:

(10)

(11)

(12)

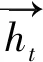
2 基于AO-VMD-BiGRU的负荷预测模型

2.1 基于AO的VMD参数优化

VMD对信号的分解效果主要取决于分解个数K和惩罚因子α的设置,但是人为设置VMD参数可能造成过分解和欠分解现象。因此,采用AO算法对VMD中分解个数K和惩罚因子α迭代寻优,寻优维度设置为2,K的寻优区间设置为[2,10],α的寻优区间设置为[0,10 000]。采用VMD损失函数作为AO算法寻优的适应度函数,计算式如下:

(13)

式中:f(t)为原始输入信号;f′(t)为分解后信号;T为时间长度。

2.2 AO-VMD-BiGRU模型结构

为实现短期电力负荷的预测精准度大幅提升的目标,提出基于AO-VMD-BiGRU的模型预测短期负荷的变化趋势,其模型结构如图3所示。首先利用损失函数作为适应度函数,运用AO对VMD中的分解个数K和惩罚因子α进行迭代寻优,确定这2个参数值;随后,把原始负荷数据导入VMD中进行简单的模态分解,获得各模态分量IMF1,IMF2,…,IMFn;最后把各模态分量导入BiGRU神经网络模型,得到各模态分量预测值,进行输出结果叠加,从而得到实际预测值。

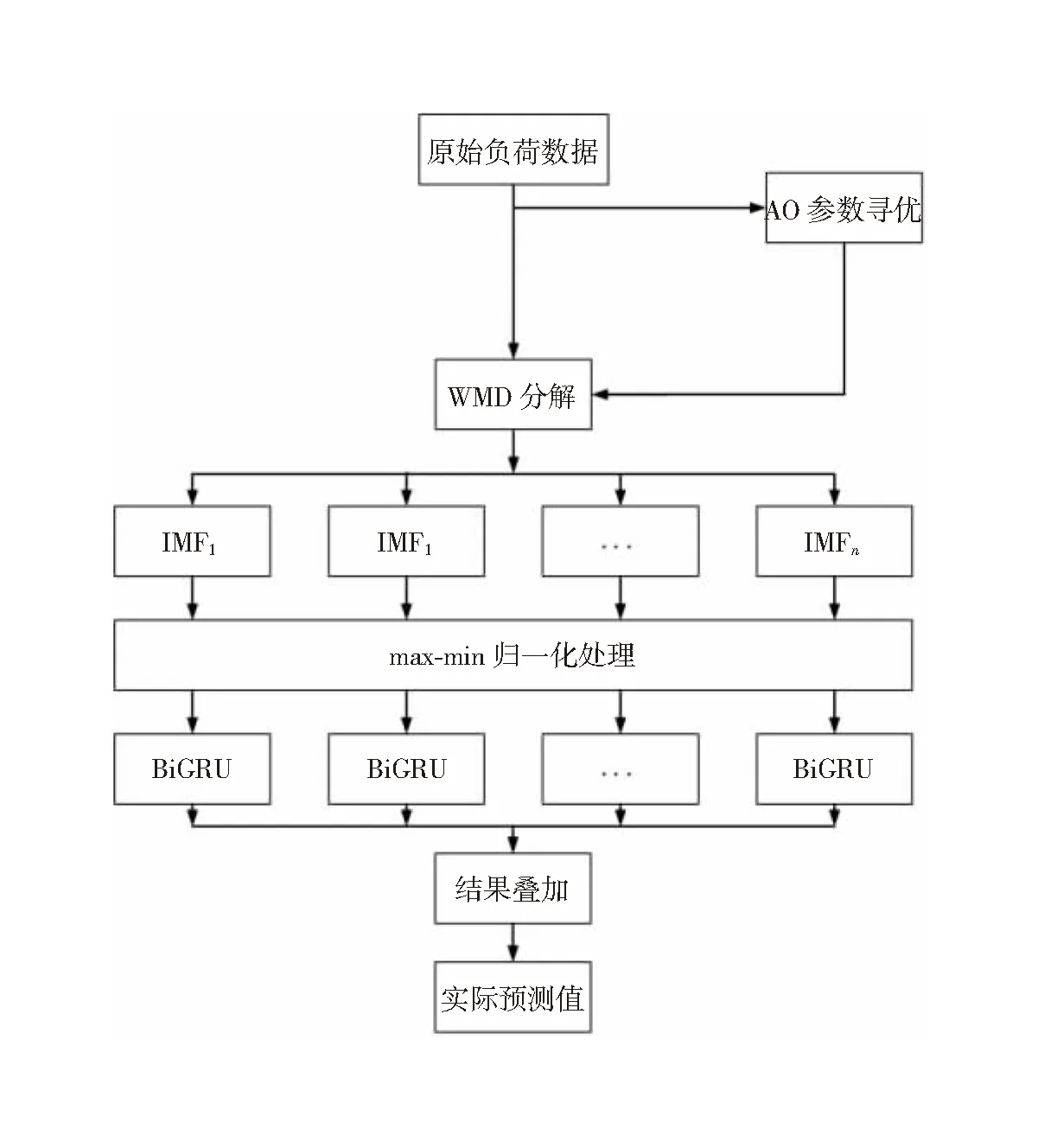
图3 AO-VMD-BiGRU模型结构图

模型评估主要依据3个重要的指标,分别是平均绝对百分比误差(MAPE)、均方根误差(RMSE)和平均绝对误差(MAE),这3个评估标准能够有效地测试负荷预测方法的性能好坏。在电力负荷预测中MAPE、RMSE、MAE的值越小,表示模型的拟合效果越好,代表负荷预测越准确,计算式如下:

(14)

(15)

(16)

式中:yi为第i个采样点真实所得到的负荷值数据;y′i为第i个采样点预测计算出来的负荷值;n值为测试的样本数。

3 试验分析

3.1 数据处理

试验数据选取澳大利亚昆士兰地区 2014年1月份上半月的真实历史负荷数据(包含干球温度、电力价格、空气湿度、电力负荷等特征)为数据集合,每天会采取48个样本值,每次采样的时间间隔是30 min,每次获取的数据包含上面提及的6个方面电力负荷数据值。

采用 min-max 标准化将数据归一化到[0, 1],计算过程如下所示。

(17)

式中:xi为第i个采样点特征原始值;xmin和xmax分别为采样数据中各特征数据的最小值和最大值;x′t为xi数据归一化后的值,范围为[0, 1]。

3.2 基于AO-VMD分解试验

为了体现AO优化VMD参数的有效性,将AO优化VMD参数和VMD参数默认值以及鲸鱼优化算法(whale optimization algorithm, WOA)优化VMD参数进行对比,所有模型的训练集与测试集相同,AO和WOA寻优VMD参数的迭代过程和分解结果如图4和表1所示,对应式(13)中分解结果越小,模型预测越准确。

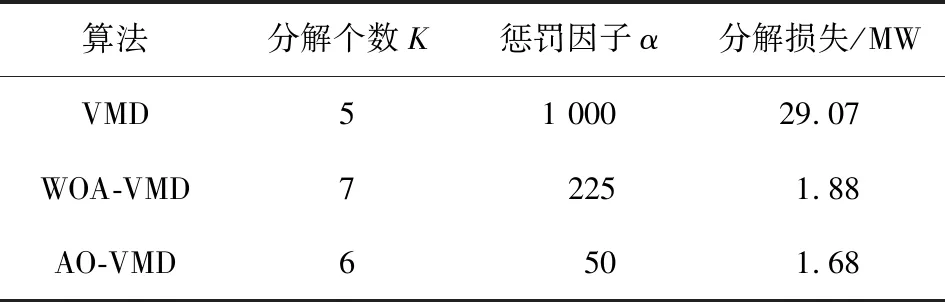
表1 VMD寻优参数结果

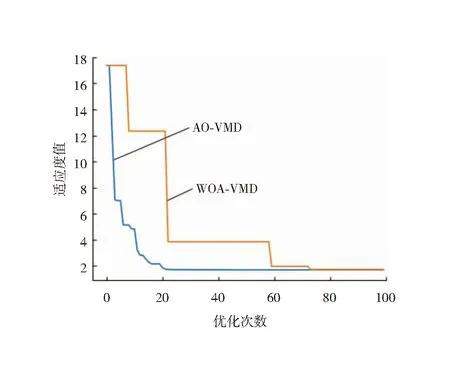
图4 不同算法迭代寻优图

由图4和表1可知,使用AO对VMD进行参数寻优相较于WOA参数寻优,寻优能力更强,寻优速度更快,其分解损失相较于一般VMD参数设置和WOA优化的分解损失更小,最小为1.68 MW。原始负荷数据和AO-VMD的分解序列如图5和图6所示,图6中res代表原始负荷数据分解的残差分量。

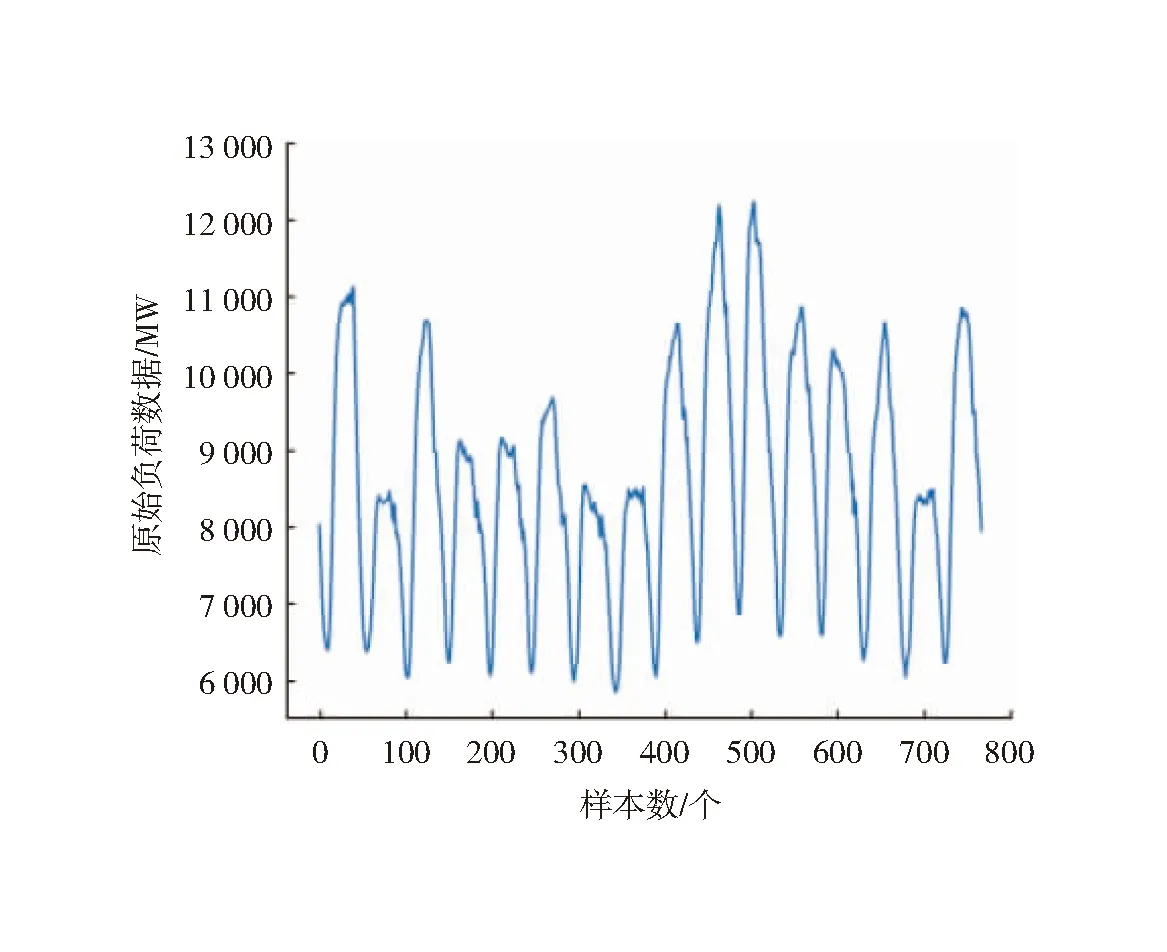
图5 原始负荷数据图

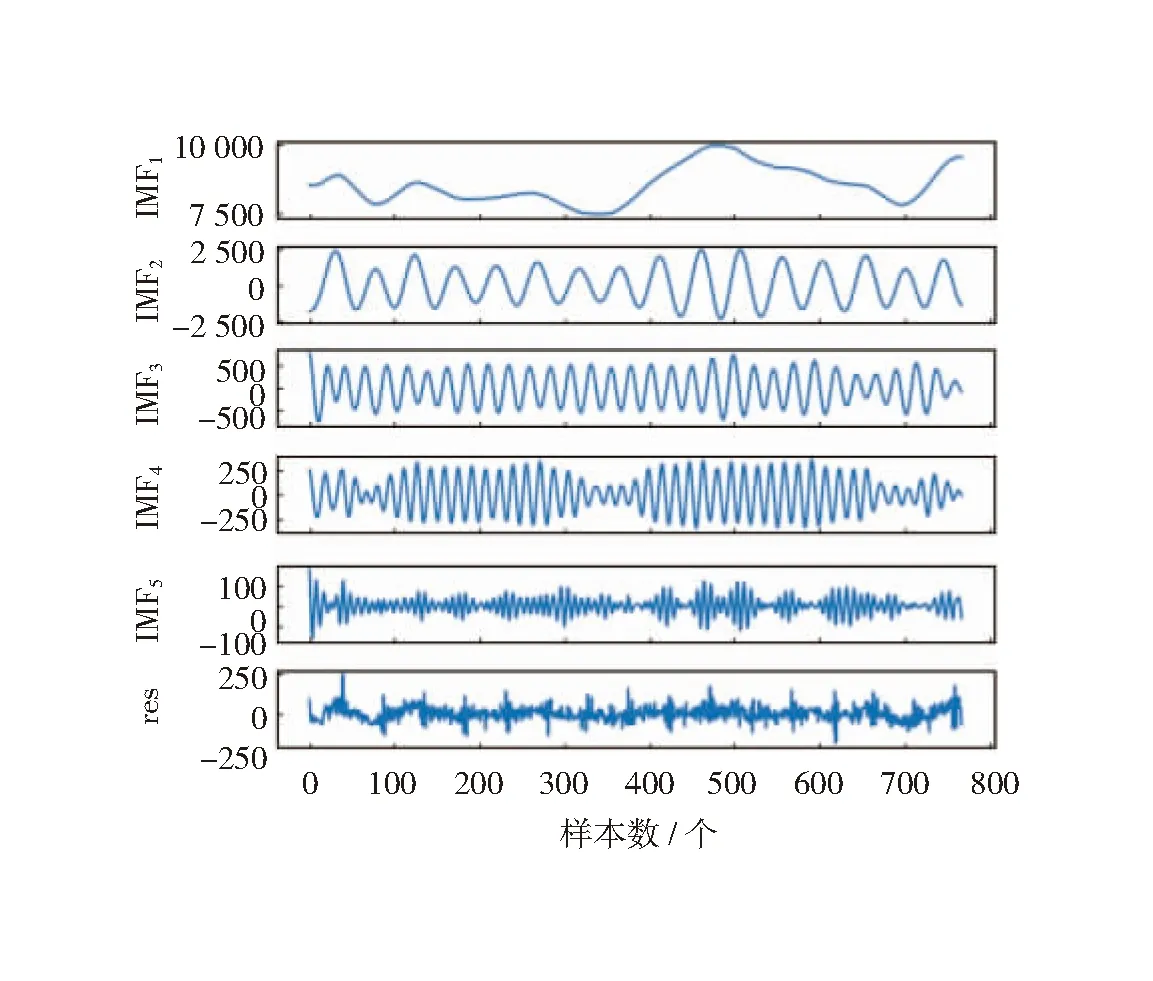
图6 AO-VMD分解序列图

3.3 试验结果分析

为验证方法有效性,试验将AO-VMD-BiGRU模型与BiGRU模型、VMD-BiGRU模型和WOA-VMD-BiGRU模型之间的性能进行了对比。在预测电力负荷数据的时候,参考文献[13]可以把这几个模型的递归神经网络层数都设置成1,而将神经网络各层的神经元数量控制在50,预测结果如图7和表2所示。

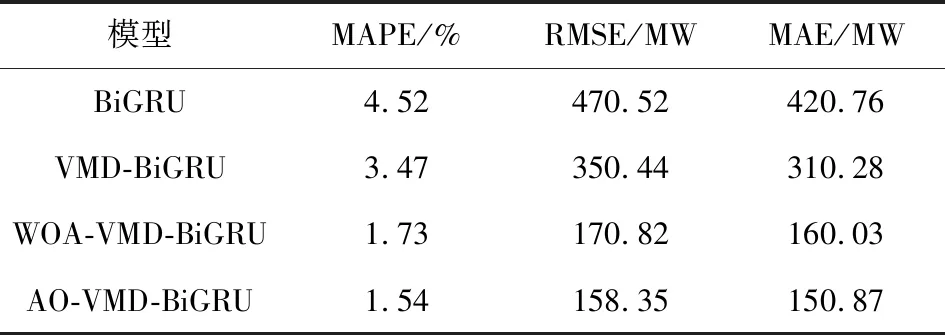
表2 各类模型对比

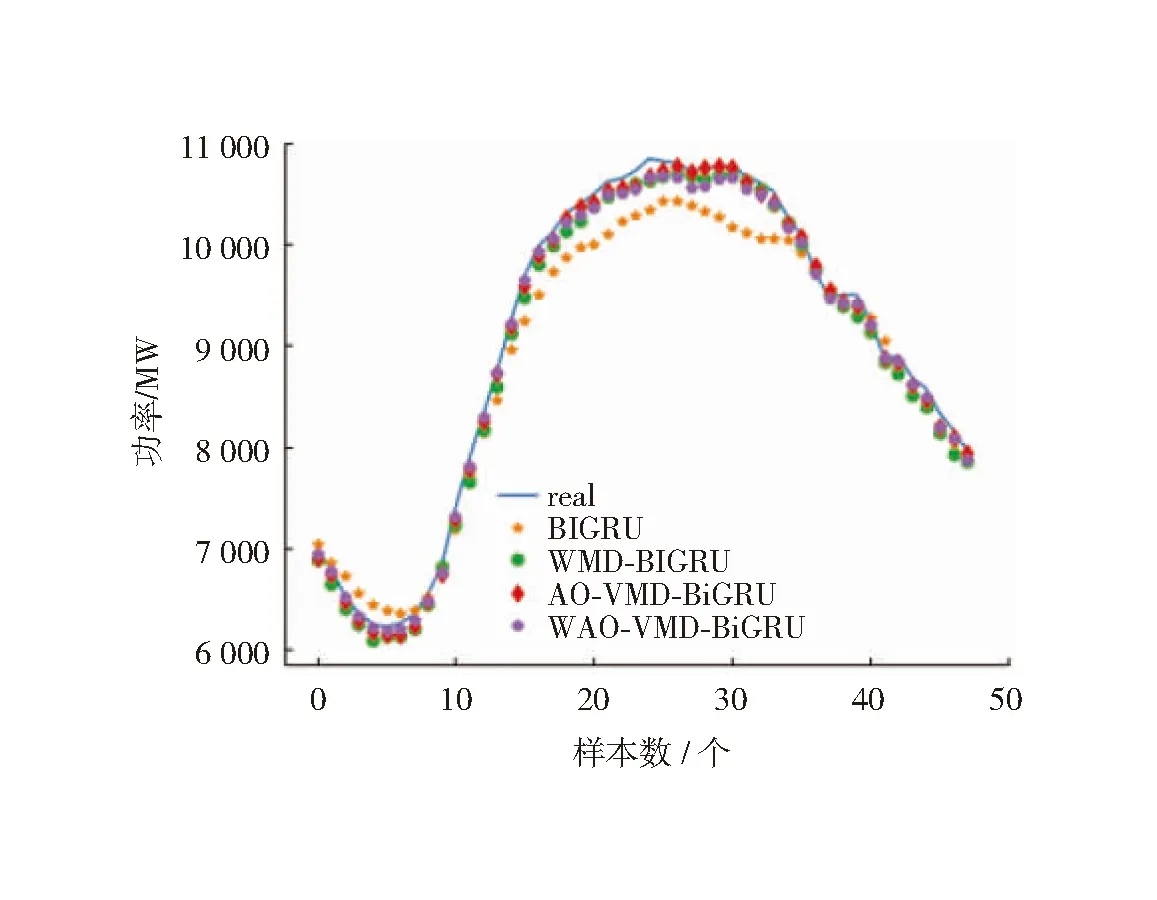
图7 预测结果对比

由表2可知,4种模型预测结果都取得了良好的效果,AO-VMD-BiGRU模型的预测结果更好。其中,AO-VMD-BiGRU模型的MAPE为1.54%,其MAPE相较于BiGRU模型、VMD-BiGRU模型和WOA-VMD-BiGRU模型这3种方法的MAPE分别降低了2.98%、1.93%、0.19%。根据图7可知,基于AO-VMD-BiGRU模型预测结果与实际负荷曲线拟合程度更高,可以很好地表示负荷变化的趋势。

4 结 语

面对电力系统对负荷预测准确性要求日益提高的形势,提出一种基于AO-VMD-BiGRU混合模型预测方法。

1)通过AO对VMD进行参数寻优,确定K和α的值,降低了人为设置参数的随机性。

2)原始负荷数据经过VMD分解,获得不同频率的模态分量,削弱了原始负荷数据的噪声干扰。

3)采用BiGRU神经网络对各模态分量进行预测并进行预测结果叠加,提升了负荷预测的精度。对比试验结果表明,此模型预测精度更加准确,具有一定的可行性。