基于形状记忆合金驱动的运输机器人设计*
胡殿刚 杨 磊 李卫东,2
1 武汉理工大学 武汉 430063 2 上海理工大学 上海 200093
0 引言
传统刚性机器人大多设计成金属结构,致动器一般是由刚性电磁部件(例如,磁体、铜和钢轴承)或由钢或铝合金材料制成的电动机,在装配线上执行快速、精确、强大和重复的位置控制任务。柔性机器人通常是受生物系统的启发,由软体材料或电活化材料驱动,实现运动或执行一些特定功能。柔性机器人有人机交互更加安全、对可穿戴设备的适应性更好、驱动系统简单等优点,在机械工程领域具有广泛的应用。
形状记忆合金(Shape Memory Alloy,SMA)因其具有较高的热稳定性、应变恢复与耐腐蚀性,常被应用于柔性机器人的致动器设计[1]。在致动器设计过程中,研究人员利用加热、加载等方式改变SMA 的形状以驱动机器人运动[2]。同时,SMA 可以通过增材制造工艺灵活生产,以支持小型、精致、高度自动化和可靠的柔性机器人设计[3-5]。
Yuk H 等[6]制作的小型爬行机器人模仿了秀丽隐杆线虫的运动。相邻的运动模块通过SMA 弹簧连接,有规律的变形可以使机器人的运动类似于真正的蠕虫。Pan J 等[7]受海星和章鱼的肌肉器官和模块化的启发,设计了一种仿生球形机器人,由SMA 弹簧驱动,使脚上下弯曲,帮助机器人在地面上爬行和滚下斜坡。Wang W 等[8]演示了一种模仿蠕虫运动的爬行软体机器人。机器人的主体是一个薄的四方复合材料板,在四周放置了2 对SMA 电线。对SMA 施加周期性电流使其变形,使机器人能够转弯和爬行。Lin H T 等[9]受毛毛虫运动的启发,利用硅酮材料和SMA 线设计了一种滚动软机器人。安装在机器人两侧的SMA 导线在电流的激励下,变形卷曲成车轮状,实现滚动。
这些设计方案共同之处在于仅能实现简单的运动,如单向移动、转向以及滚动。SMA 致动器的输出力较小,承载能力弱或者几乎没有,在应用与功能方面存在不足。因此,本文提出一种SMA 驱动的运输机器人,不仅能够实现直线移动,还具有一定运输能力,拓展了柔性机器人的应用场景。
1 机器人设计
在设计机器人的过程中需要解决2 个问题:进行周期性变形伸缩的驱动部分用于提供机器人前进驱动力和要对前后支腿与地接触面作摩擦系数差异化处理,重点是要改变前腿运动中与地面之间的摩擦系数,实现让仿生机器人前后支腿在锚定与运动之间的状态切换。针对这2 个问题,本研究提出对应的解决方案:1)选择双程SMA 弹簧作为仿生机器人的驱动装置。该弹簧具有双程记忆功能,在温度变化下能够周期性地变形伸缩,提供驱动力。2)将前腿与地接触面分成前后2 个部分,前部打磨光滑,后部贴上美纹纸以增大摩擦,保证前腿前部、前腿后部与后腿处与地之间摩擦系数不同,从而使前后支腿交替运动。
基于上述方案,本研究提出了基于SMA 弹簧驱动的设计方案。如图1 所示,该机器人采用后腿驱动,前后支腿交替移动,以模仿尺蠖的运动行为。SMA 弹簧驱动器安装在机器人的后腿支撑台上,与机器人主体底部连接。

图1 机器人结构设计简图
该方案设计机器人实现连续周期移动,单个周期可以分成2 个运动阶段,如图2 所示。通入电流后,SMA弹簧温度升高,发生变形并驱动后腿向前运动,前腿锚定于地面上;当弹簧完全伸长后,停止通电加热,弹簧随即冷却收缩并驱使后腿原地转动,前腿向前位移。在驱动装置的一个运动周期内,机器人驱动通过弹簧变形收缩实现,而前后支腿的交替运动则通过与地面的摩擦系数的变化来实现。该方案令SMA 弹簧独立作为驱动模块,同时弹簧作为承载结构支撑躯体运输物件。

图2 方案设计运动机理图
1.1 驱动模块
双程SMA 的变形原理为:根据温度的变化,SMA晶体结构在去孪晶马氏体与奥氏体之间互相转换,当温度升高时,SMA 开始发生变形,晶体结构从去孪晶马氏体转变成奥氏体状态,温度降低时,SMA 回复至加热前的去孪晶马氏体状态。本文选用的双程SMA 弹簧的截面直径为15 mm,长度为10 mm,丝径为1 mm。
为分析SMA 在温度变化下的相变行为,同时测定马氏体形成开始与完全温度、奥氏体形成开始与完全温度,本文使用差示扫描量热仪分别将样品从20 ℃加热到100 ℃,再从100 ℃冷却至20 ℃,温度变化速度设计为5 ℃/min。为分析SMA 在温度变化下的相变行为,分别测量不同时刻下的样品温度与热流值,通过Origin 绘图软件绘制出时间—温度与时间—热流曲线;为测定SMA 相变的起止温度范围,应用切线法,得到SMA 马氏体与奥氏体的相变温度。如图3 所示,在SMA 样品升温阶段,晶体结构从马氏体状态相变至奥氏体状态,样品吸收热量,对应补偿热量值为负。结合热分析曲线,可获知相变过程起始时刻在6 min 30 s,与峰值点2 点处做曲线切线,得到的交点系奥氏体相变开始时的温度,即As,对应加热温度为56.5 ℃;相变过程结束时刻在14 min 30 s,与峰值点处的切线交点对应加热温度为66.2 ℃,系奥氏体相变完全时的温度,即Af。

图3 双程SMA 热分析曲线
在样品降温阶段,晶体结构从奥氏体状态相变至马氏体状态,样品释放热量,对应补偿热量值为正。相变开始时刻为24 min 30 s,与峰值点处的切线交点对应温度值为59.6 ℃,系马氏体相变开始时的温度,即Ms;相变结束时刻为28 min 30 s,与峰值点处的切线交点对应温度值为42.7 ℃,系马氏体相变完全时的温度,即Mf。
由于SMA 本身是一种合金材料,主要成分是Ni、Ti 等金属,有一定的电阻,通入电流后,SMA 产生热量、温度值升高。因此,采用通电直接加热来改变SMA 温度是一种最为容易的实现方式。
当SMA 弹簧负载为零时,测得初始长度为14 mm,通入电流后,得到弹簧在不同电流下的变形时间变化,如图4 所示。弹簧在加热伸长阶段,电流值与弹簧变形的伸长时间呈负相关,即通入的电流值越大,弹簧所需要的变形时间更短;平均伸长量为25.9 mm,当电流值提高到2.5 A 时,伸长量达到最大值,为27.8 mm;当弹簧进入冷却收缩阶段后,所需要的收缩时间保持恒定,不会受到通入电流值的影响,平均时间为82.9 s。
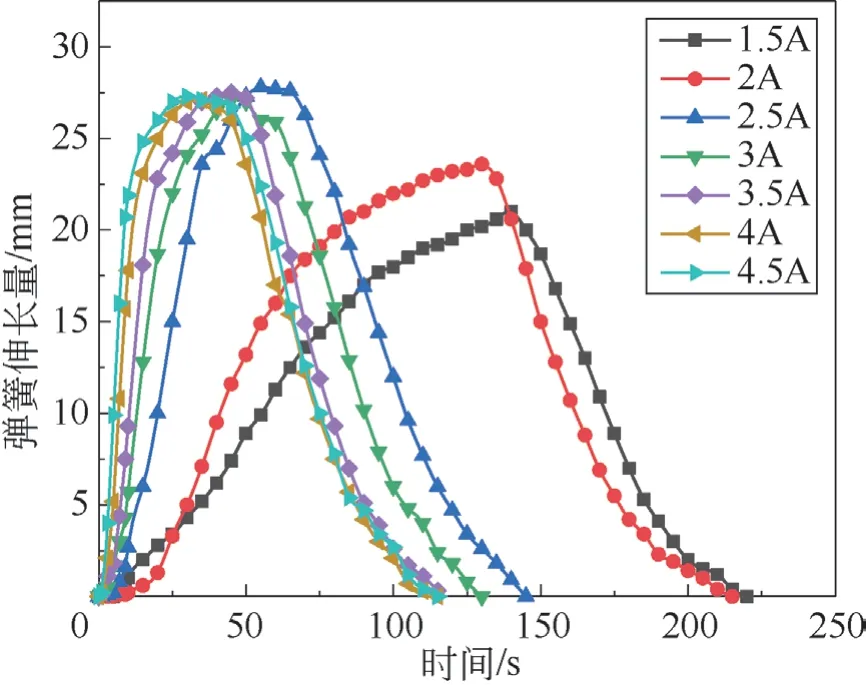
图4 空载下弹簧伸长量拟合曲线
在空载情况下,弹簧加热阶段的变形速度与电流呈正相关,具体影响机制可以总结为通入弹簧的电流越大产生的热量越多,温度上升速度更快,达到SMA 相变温度点所需时间更短,变形速度变快。然而弹簧变形速度是有极限的,当电流继续增加到2.5 A 以上时,弹簧变形增速逐渐放缓。
1.2 主体模块
如图5 所示,机器人主体模块包括前后支腿以及运输仓,为使机器人具有更大的负载能力,同时与驱动弹簧形成良好的配合,对零件的尺寸、结构进行设计。

图5 机器人组装图
前腿尺寸参数设计高度30 mm,厚度5 mm。结构设计上,前腿的上端嵌入到运输仓的前腿凹槽中并与运输仓刚性连接,下端呈半圆形,与地面接触,且下端前后面的摩擦系数不同。当机器人重心发生变化时,前腿下端与地面产生滑动摩擦,通过前腿与地面的摩擦力的变化使前腿处于锚定或滑动状态。
后腿设计尺寸参数为高度25 mm,腿部厚度3.5 mm,托板长度30 mm,厚度4 mm。后腿结构整体分成与地面接触的支腿和安置弹簧的托板2 个部分,考虑到弹簧安装时因自身的长度会使支腿与主体之间存在一个夹角(在实际安装时测得为10°),故将后腿的支腿部分与托板之间设置夹角为80°。如此,可以使后腿的支撑部分近乎垂直于地面,在SMA 弹簧驱动下,支腿前倾,减小运动时与地面的阻力。
运输仓主体尺寸参数设计为80 mm×40 mm×21 mm;整体结构分成上下2 个部分,上部是1 个方型仓,可以添加配重;下部切出3 个凹槽,分别是用于安装前腿、后腿以及SMA 驱动弹簧。
2 运动学分析
为了使该仿生机器人的运动分析过程简化,本研究做出如下假设:
1)机器人在运动过程中由于自身重力作用以及在运动过程中产生摩擦力与惯性力,不考虑二者对机器人主体的变形产生的影响;
2)在仿生机器人运动过程中,当支腿处于锚定状态时,支腿与地面受到最大静摩擦力,并且最大静摩擦力大小等同于滑动摩擦力。
2.1 模型建立
如图6 所示,将仿生机器人作为平面对象进行运动学分析,以仿生机器人右下位置作为坐标原点,建立二维坐标系。机器人前进方向作为坐标轴x轴的正方向,垂直与地面向上的方向作为坐标轴y轴的正方向。在实际运动中,前、后支腿与地面之间为线接触,在二维坐标系中简化成点。其中,机器人前腿与地面的接触点记作A,摩擦力记作f1;后腿与地面的接触点记作B,摩擦力记作f2;机器人的质心记作C。

图6 仿生机器人受力分析图
机器人在运动过程中的位移方程表达式为
式中:xA为机器人前腿与地面接触点A相对质心C在x轴上的位移,yA为机器人前腿与地面接触点A相对质心C在y轴上的位移,xC为质心C在x轴上的位移,yC为质心C在y轴上的位移。
根据受力分析图,机器人质心在x轴以及y轴方向上受力平衡,得到运动方程为
式中:M为机器人整体质量,g为重力加速度,fA为地面对前腿接触点A的摩擦力,fB为地面对后腿接触点B的摩擦力,NA为地面对前腿接触点A的支持力,NB为地面对后腿接触点B的支持力。
本文将机器人的一个运动周期分成2 个阶段,如表1 所示,记录各阶段运动状态以及受力情况。表1 中t1为SMA 弹簧通电加热时间,T为机器人一个运动周期。

表1 各阶段运动状态与受力情况
为实现仿生机器人的爬行运动,需要保证前、后支腿与地面接触的摩擦力不相等。前面提到在第1 阶段运动过程中,前腿与地面的静摩擦力要大于后腿的滑动摩擦力以防止前腿后滑,SMA 弹簧可以通过变形伸长驱动后腿向前运动。当SMA 弹簧冷却收缩时,后腿与地面的静摩擦力需大于前腿的滑动摩擦力,从而利用后腿的摩擦力驱动前腿移动。假定支腿A和B处受到的正压力相等,前腿前端的摩擦系数为μA1,后端的摩擦系数为μA2,后腿处的摩擦系数为μB,且μA1>μB>μA2。
2.2 第1 阶段运动分析
在0-t1阶段,SMA 通电加热,驱动后腿与地面接触点B向x轴正方向运动,如图7 所示。此时前腿处于原地转动状态,与地面的接触点A处于相对静止状态,此时前腿接触点A与后腿接触到B的位移值xA1(t)与xB1(t)可表示为

图7 后腿前后阶段运动变化示意图
式中:a为后腿托板与弹簧连接处到支点O的距离;b为后腿与地面接触点到支点O的距离;α为初始状态下弹簧托板与主体下底面的夹角;θ为SMA 弹簧的角位移;ζ(t)为SMA 弹簧的伸长量,受弹簧通入电流与负载影响。
在弹簧伸长阶段内,只有机器人的后腿发生位移,而机器人整体在x轴方向上并未发生位移,x1(t)=0。根据位移方程表达式可得质心位移
在这一时间段内,前腿处于相对静止,受到地面静摩擦力作用,方向为x轴正方向;后腿处于滑动状态,受到地面的滑动摩擦力,方向为x轴负方向,2 个摩擦力大小关系为
要实现后腿B向x轴正方向移动的同时前腿A保持静止,需满足
即可得到质心在x轴方向上的加速度值为
2.3 第2 阶段运动分析
第2 阶段弹簧冷却收缩至初始形状。此时需要保证后腿处于相对静止状态,即受到地面的静摩擦力作用,弹簧产生的拉力驱动前腿向前移动,与地面产生滑动摩擦力,最终实现机器人整体的位移。
此时前后支腿A和B处的摩擦力大小关系式为
同理,为了保证前腿接触点A向x轴正方向运动的同时后腿接触点B保持相对静止,需满足
由此得出质心C在x轴方向上的加速度为
在这一阶段的运动过程中,机器人受到的外力主要是地面作用在前、后支腿A和B上的摩擦力,并且在运动过程中,2 处摩擦力的大小与方向均未发生变化。因此可以假定机器人质心C在这段运动中做匀减速运动,期间质心C的速度及位移的表达式为
可得质心位移为
而质心在一个运动周期T内的总位移值表达式为
3 负载运动
本试验利用直流电源调节SMA 弹簧的通入电流,试验电流设置为4 A;机器人负载设计为100 g;每次运动试验的记录时间设置为120 s,每5 s 记录SMA 弹簧的变形量、前后支腿以及机器人整体的位移量,并拍摄机器人运动过程图,结果如图8、图9 所示。在120 s 内,机器人总计完成4 个运动周期,平均运动时间30 s。弹簧的平均伸长时间与伸长量为15 s 与10.5 mm。机器人前后支腿以及整体的总位移量分别为2.5 mm、2.5 mm与3 mm,对位移曲线计算斜率,得到各自的最大运动速度分别为1 mm/s、0.4 mm/s 与0.3 mm/s。

图9 100 g 负载下机器人各部分以及整体运动数据
4 总结与讨论
本文基于对双程SMA 的变形机理研究,提出一种新型的运输机器人设计,并通过运动学分析与负载运动试验验证了该设计方案的可行性。SMA 弹簧基于双程形状记忆效应,能够实现双向变形,使机器人可以稳定地往复运动。同时该机器人具有一定的运输能力,可以承重100 g 的负载(相当于自身质量的3 倍),最大运动速度可以达到0.3 mm/s。尽管该机器人尚处于起步开发阶段,但能够以远程控制的方式启动机器人,在空间狭长、高空、管道等工况下有着显著优势。

