综合评价指标约简算法综述

余良武，郭文勇，黄家宁，伍哲，曹辰昊

（海军工程大学，武汉 430033）

0 引言

综合评价问题本质上是多个指标构成的信息系统的决策问题，正确选择评价指标是决策准确的基础和前提。在综合评价问题中，指标体系初构更多的是强调指标的全面性，要求所选择指标能够从多个角度全方位刻画系统，“求全而不求精”，因此存在一定程度的信息冗余。信息冗余一方面会增加指标监测和数据运算的工作量和成本，另外一方面还会因重复计算而给综合评价结果的准确性带来负面影响，因此指标的“全”和“精”是一对矛盾体，为了在二者之间寻求最优平衡，需要采用合适的方法对评价指标集进行约简。指标约简是指标体系从“全”到“精”的过程，也是综合评价不可或缺的环节。本文系统地研究了目前常用的几种指标约简算法的原理并对其应用场合及优缺点进行了综述。

1 指标约简算法分类

“属性约简”概念提法多见于粗糙集理论，是粗糙集理论的核心内容之一，指在保持知识库分类能力不变的条件下删除冗余和不重要属性，达到提取数据特征、简化知识运算的目的[1]。应用于综合评价领域时，很多学者称其为指标筛选或指标约简[2-3]。延伸到粗糙集理论范畴之外，早期也有学者应用统计学方法实现相似的功能，因此广义的指标约简算法包括统计学方法和粗糙集理论两大方面，如图1所示。

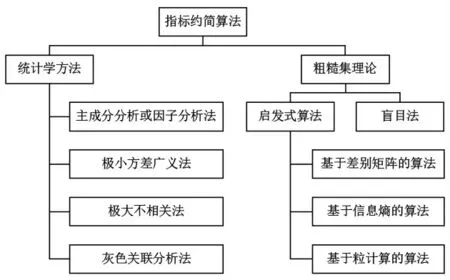
图1 典型指标约简算法

2 基于统计学方法的指标约简算法

当系统各指标存在一定规模的较完备统计数据时，可应用统计学方法进行指标约简，这也是粗糙集理论广泛应用前使用最多的指标约简和特征提取方法。主要思想是，通过分析统计数据，判断条件指标之间或条件指标与决策指标之间的相关程度，进而通过一定的标准和方法删除冗余指标或构造新的少数几个不相关指标。具体包括主成分分析法、因子分析法、极小方差广义法、极大不相关法、灰色关联分析法等。

2.1 主成分分析和因子分析法

主成分分析法（Principal Components Analysis, PCA）根据指标间相关关系，通过线性组合，构建线性无关的综合指标即主成分：

式中：Yi（i=1，2，…，p）为主成分；Xi（i=1，2，…，p）为原始指标，写成矩阵的形式为

通过提取累积贡献率达到一定水平，能够反映原始指标大部分信息的少数几个主成分达到指标约简的目的；因子分析是主成分分析的推广，可理解为主成分分析的逆问题[4]，将各原始指标分解为公共因子和特殊因子两部分：

式中：Fj（j=1，2，…，m）为公共因子；εi为特殊因子。

写成矩阵的形式为

同样，通过抽取累积贡献率达到一定水平的少数几个公共因子达到指标约简的目的。因子分析中由于因子载荷具有不唯一性，相比于主成分分析法，能够提高解释能力。尽管如此，由于主成分分析法和因子分析法构造了新的变量，这些新变量并没有直接的物理意义，要对这些变量做出直观解释也是十分困难的。另外，主成分分析法和因子分析法所研究的指标约简大多存在于特征提取层面，能够简化后续数据处理和运算，但是必须以原始指标测量值为基础，因此并未减少实际的指标测量工作量。

2.2 极小广义方差法

广义方差D（X）定义为X的协方差矩阵Cov（X）的行列式或者其他相应函数，能够从整体上衡量指标的分散性[5]。极小广义方差指标约简算法的基本思想是：如果删除某个指标后条件广义方差变化很小，则表明该指标所包含的信息量在总体中占有很大份额，即具有很强代表性，因此，可根据条件广义方差最小原则依次提取最具代表性的R个指标作为约简集。R值的设定没有固定的理论依据，一般根据评价者的主观经验和需要设置，因此极小广义方差法具有较强的主观性。

2.3 极大不相关法

极大不相关法以指标间的相关程度为依据，认为和其他指标相关程度较高的指标所携带的信息可很大程度上由其他指标描述，因此在约简过程中可以删除。具体过程为依次计算各指标与剩余指标的复相关系数，剔除复相关系数最大的指标，重复操作，直到剩余预期数量的指标。极大不相关法和极小广义方差法类似，同样也存在主观性强的缺点。

2.4 灰色关联分析法

灰色关联分析法，定义了条件指标的重要性测度和条件指标之间的影响力测度，通过去重叠化计算条件指标的绝对重要度，和约简阈值比较，决定条件指标是否进入约简集[6]。该方法中约简阈值的设置具有一定的主观性，另外条件指标重要度的概念是和决策指标比较的结果，因此一般只适用于决策系统，无法应用于缺少决策指标的信息系统。也有部分学者选择最为重要的特定指标来代替决策指标，在粗糙集指标约简方法研究中也有类似的做法，但是实际上这种做法的合理性有待商榷，决策指标是所有条件指标综合作用的结果，是任何单一指标无法替代的。

统计学指标约简算法常常结合聚类分析法和判别分析法使用，在进行指标约简前对所有指标进行分门别类，一方面可减少约简工作的计算量，另外一方面也保证了信息的全面性，这种做法和指标体系层次构造过程中所使用的思想是一致的。统计学指标约简算法通过挖掘数据本身蕴藏的信息，发现冗余并加以剔除，其优点在于需要的先验知识少，可以直接处理连续型数据，无需离散化处理。但是，相对于基于粗糙集理论的指标约简算法，统计学指标约简算法的突出缺点是并不以保持知识库分类能力不变为前提，缺少约简目标导向，最终获得约简集的规模具有很大的主观随意性，常常出现约简后分类能力改变的现象。

3 基于粗糙集理论的指标约简算法

粗糙集理论（Rough Set Theory, RST）由波兰的Pawlak教授于1982年提出，是一种研究不确定、不精确、不完备、不一致知识和数据的数学工具[7]。其应用研究主要包括指标约简、规则获取、基于粗糙集的智能算法等方面，目前已广泛应用于交通运输、工业控制、社会科学、医疗卫生和军事等领域[8]。基于粗糙集理论的指标约简是一个N-P Hard问题[9-10]，许多学者对其进行了研究，力求提高约简效率，提出许多各具特色的算法。根据有无信息启发，可分为盲目删除法和启发式算法，盲目删除法无任何信息指导，依次删除一个指标，检验知识库分类能力是否改变，简单易懂，但是存在组合爆炸问题，时间和空间复杂度都很高。启发式算法以某种信息为启发，以指标核为起点，选择符合条件的指标加入约简集，能够很大程度上减少搜索空间，降低时间和空间代价，是目前常用的方法[11]。

3.1 基于差别矩阵的指标约简算法

基于差别矩阵的指标约简算法由Skowron教授于1991年提出，差别矩阵在不同的文献中也被称为Skowron可分辨矩阵、可辨识矩阵、区分矩阵等。设知识表达系统S=（U，A，V，f），A=C∪D，其中C为条件指标集，D为决策指标集，且D≠Φ，差别矩阵MS为矩阵，元素mij定义为：

可以看出，mij为可以区分对象ui和uj所有条件指标的集合。列出MS后可通过一定的运算规则求得相对约简。对于基于差别矩阵的指标约简算法，为提高约简效率，一直以来研究较多的是向核中添加指标所依赖的启发信息，其中包括指标重要性[12-13]、指标序[14]、指标频率等[15]。二进制差别矩阵可视为差别矩阵的延伸，基本原理大致相同，不同的是差别矩阵的构建规则，二进制差别矩阵每一列对应一个条件指标ci，每一行对应一个决策指标不相同的对象对（up，uq），元素m（（p，q），i）定义为：

由于使用了0、1编码的二进制矩阵，相对于差别矩阵，空间复杂度至少降低一半，运算也更加简便。基于差别矩阵的指标约简算法一般多用于决策系统的指标约简，在信息系统中的应用较少。

3.2 基于信息熵的指标约简算法

基于信息熵的指标约简算法引用信息论中的信息熵概念，定义了指标集合的信息熵、条件信息熵和互信息等概念，将条件信息熵或互信息作为启发信息，以减少约简过程中的搜索空间。其中比较有代表性的包括MIBARK算法、CEBARKNC算法和CEBARKNCC算法。MIBARK算法以核指标集为起点，以条件指标和决策指标的互信息为启发，当互信息相等时终止运算。CEBARKNCC算法和CEBARKNC算法均以决策指标相对于条件指标集的条件熵为启发，不同的是CEBARKNCC算法以核指标集为起点，选择使条件熵最小的非核条件指标加入，而CEBARKNC算法以初始条件指标集为起点，依次删除条件熵最大的条件指标。当核值比靠近0时CEBARKNC算法具有较低的时间复杂度，当核值比靠近1时MIBARK算法和CEBARKNCC算法具有较低的时间复杂度。

3.3 基于粒计算的指标约简算法

粒度化的思想首先由美国加州大学的L.A.Zaedh教授于1979年提出，主张知识是颗粒化的，通过把复杂问题化为“信息粒”，实现复杂问题简单化，进而可利用粒计算理论中分而治之、多视角和多层次的思想方法处理信息和数据[16]。在后期的研究中L.A.Zaedh教授又指出人类的认知基础包括粒化、组织和因果关系3个基本概念，其中粒化是将整体分解为颗粒，组织是颗粒有机构成整体，因果关系则涉及原因和结果的内部联系。从哲学角度看，粒计算是一种结构化思想方法[17]。在粗糙集理论体系中，知识对应的不可分辨关系表现出显著的颗粒特征，因此粗糙集理论被视为除模糊集合理论和商空间理论外的另一粒计算所依赖的基础理论[18]。基于粒计算的指标约简算法将知识粒度本身或其衍生出的重要性测度作为约简过程中的启发信息，能够提高约简效率，而且适用于完备或不完备信息系统的指标约简。

4 结语

统计学指标约简算法的原理是挖掘数据本身蕴藏的信息，发现冗余并加以剔除，其优点在于需要的先验知识少，突出缺点是可能会出现约简后分类能力改变的现象。基于粗糙集理论的指标约简算法优点是以保持知识库分类能力不变为前提，具有鲜明目标导向，缺点是大多适用于决策指标集非空的决策系统，同时计算量较大。具体到详细的算法：主成分分析法和因子分析法构造了无直接物理意义的新变量，难以做出直观解释，另外，这两种方法所研究的指标约简大多存在于特征提取层面，能够简化后续数据处理和运算，但是必须以原始指标测量值为基础，因此并未减少实际的指标测量工作量。极小广义方差指标约简算法R值的设定没有固定的理论依据，因此极小广义方差法具有较强的主观性，极大不相关法同样也存在主观性强的缺点。灰色关联分析法约简阈值的设置具有一定的主观性，另外条件指标重要度的概念是和决策指标比较的结果，因此一般只适用于决策系统，无法应用于缺少决策指标的信息系统。基于差别矩阵的指标约简算法要求决策指标集非空，一般多用于决策系统的指标约简，在信息系统中的应用较少。基于粒计算的指标约简算法将知识粒度本身或其衍生出的重要性测度作为约简过程中的启发信息，能够提高约简效率，而且适用于完备或不完备信息系统的指标约简。