基于函数型数据的网拍虚假出价动机及影响识别
曹 珂,严明义
(1.西安财经大学 统计学院,陕西 西安 710100;2.西安交通大学 经济与金融学院,陕西 西安 710061)
0 引 言
随着网络信息技术的不断发展,线下拍卖中的虚假出价行为不可避免地出现在网络拍卖中。虚假出价(shill bidding)是以人为抬升最终成交价格为目的的网络拍卖欺诈行为。互联网交易的匿名性和多数竞拍者无意识地纵容为识别和阻止网络拍卖虚假出价行为的发生带来困难。
目前已有一些研究关注到拍卖市场中的虚假出价行为,但由于研究前提假设的不同,所得结论并不一致[1-5]。Chen Kong-ping(2018)[6]通过对虚假出价程度与拍卖成交价格的分析发现,虚假出价的存在会增加成交价格,而保留价格则会降低成交概率进而减少期望收益。林菡密和孙绍荣(2015)[7]对第一价格密封拍卖中的竞拍者串谋行为进行分析,建立了串谋双方的竞价模型,认为串谋方的虚假出价策略与估价、竞拍者人数有关。王宏(2019)[8]在独立私有价值假设下对多单位网络拍卖中的虚假出价行为展开分析,认为卖者的最优虚假出价策略是在拍卖开始时选择低的托投标,在观察到虚假出价信息后将托投标动态调整至最优水平。
从研究方法来看,拍卖数据由于虚假出价时间的不可预测性和不等间隔性,无法应用传统的统计、计量方法。Ramsay(1982)[9]在其论文中将具有这种特征的数据首次命名为函数性数据(functional data,FD)。这些样本数据的产生过程是一个函数过程,由于函数性数据不同于传统统计方法所分析的时间序列数据(time series data)和横截面数据(cross- sectional data),也不同于计量经济学中讨论的面板数据(panel data),因此,传统的数据分析方法在具体应用中受到了挑战[10]。
基于此,该文在关联价值的假设下,从期望收益变化角度定义卖者参与虚假出价的动机、阐述虚假出价动机产生路径。其次结合竞拍者出价到来的非齐次泊松过程特征,应用函数型数据分析方法构建卖者虚假出价参与动机阶段变化模型,对卖者参与虚假出价的动机进行量化分析,详细阐明卖者参与动机随时间、竞拍者人数以及拍品价值的影响变化情况。最后,结合所得结论,提出具有针对性的措施建议,以期能够减少网络拍卖中虚假出价行为发生,维护网络交易公平公正,提升拍卖市场运行效率。
1 理论模型假设与构建
1.1 模型假设

(1)信息关联价值假设。


(2)竞拍者到来过程分布假设。
实证研究发现,网络拍卖中竞拍者的虚假出价人数具由显著的阶段性特征[11],大多数拍卖中竞拍者的到来速率表现出明显的波动性,该过程具有非齐次泊松过程特征。
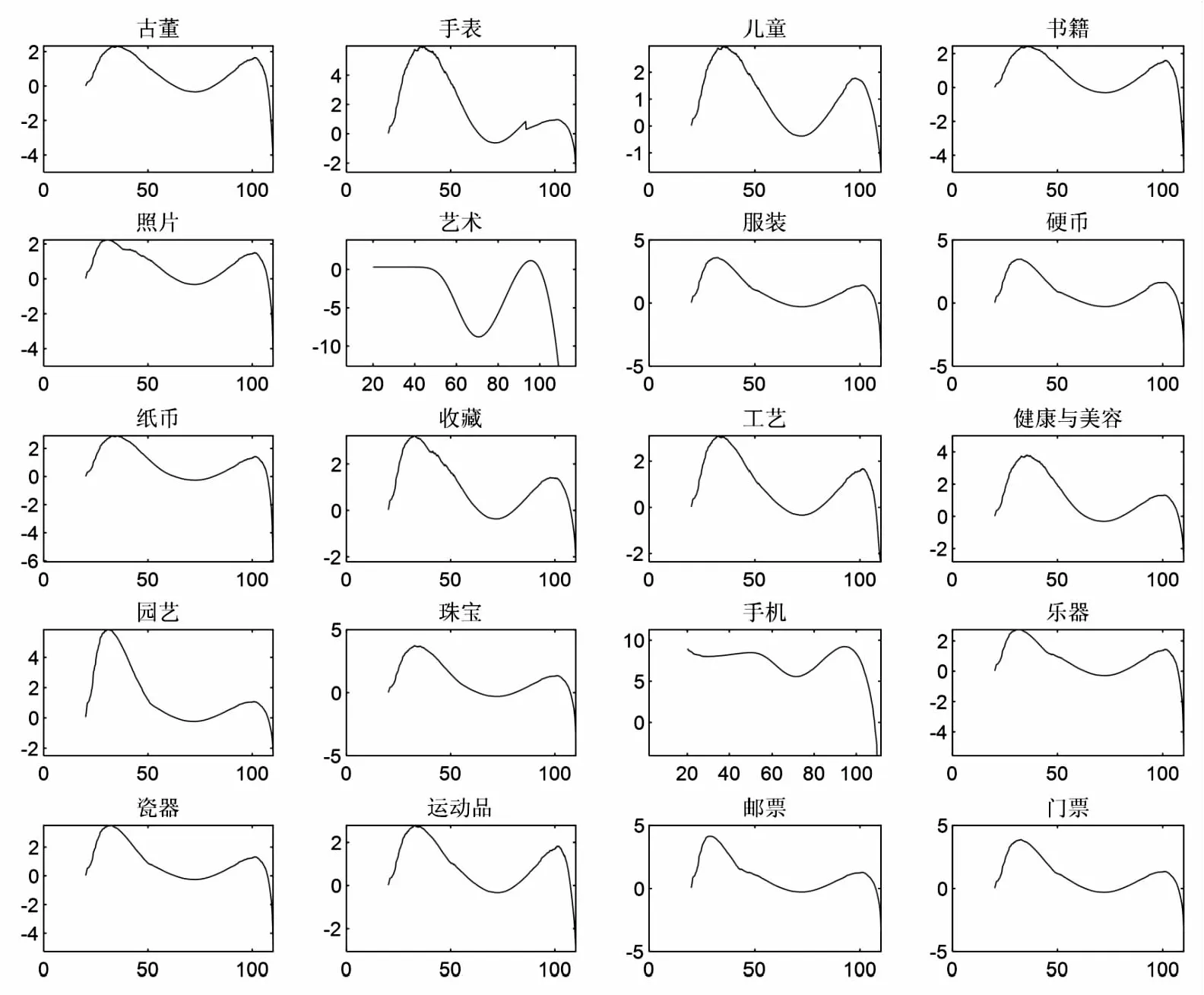
假设在一场网络拍卖中,拍卖期限为[0,T],第i个竞拍者的到来时刻为ti且0 (1)N(0)=0。 (2){N(t),t≥0}具有独立增量。因为第i个竞拍者的到来是否发生主要依赖于上一位竞拍者的虚假出价金额,同样依赖于上一个虚假出价发生的时刻ti,而与ti之前的时刻无关,即时刻t的虚假出价次数N(t)与(t,t+s]的虚假出价次数N(t+s)-N(t)相互独立。 (3)由于截止效应(deadline effects)[12]和早期效应(earliness effect)的存在[13],竞拍者的到来速率在一场拍卖中的波动具有阶段性,是时变的。 (4)当时段长度h很小时,总会有: P{N(t+h)-N(t)=1}=λ(t)h+o(h)和 P{N(t+h)-N(t)≥2}=o(h) 综上所述,网络拍卖中竞拍者的到来过程具有非齐次泊松过程的所有特征,应用非齐次泊松过程对其进行描述。 (1)不存在虚假出价的卖者期望收益。 令保留价格(reserve price)为r,是卖者以自身期望值提前设定好的价格,任何低于保留价格r的虚假出价将不会成交。竞拍者i以信号xi为参考的虚假出价函数在保留价格r附近是不连续的,即在保留价格r附近将不会有虚假出价。因此,可根据由保留价格r确定的临界值x得到不存在虚假出价时卖者的期望收益,共由两部分组成:当次高虚假出价是保留价格时的卖者期望收益与次高虚假出价来自于活跃的竞拍者时的卖者期望收益之和,由Ucom(x)表示: Ucom(x)=(F(2:n)(x)-F(1:n)(x))·w(x)+ (1) (2)存在虚假出价的卖者期望收益。 (2) 根据一阶条件,最优虚假出价为: b(x)=α(x)w(x)+(1-α(x))·v(x) (3) (4) (3)虚假出价动机模型构建。 假设拍卖时长为[0,T],根据竞拍者到来的阶段性变化模式,可以证明竞拍者到来的速率函数λ(s)具有如下三个阶段的具体数学表达式: λ(s)= (5) 其中,参数c>0,αj>0(j=1,2,3)均为常数,T为拍卖的已知时长,d1、d2为不同阶段时间划分点且0≤d1 拍卖结束时,如果总竞拍者人数为n,即N(T)=n,则竞拍者到来发生时间的分布函数为: M(s)= (6) 式中: 相应的密度函数为: (7) 将存在虚假出价时卖者期望收益表达式(4)重新整理得到基于竞拍者随机到达的卖者期望收益: F(s)n-2f(s)ds (8) 类似的,通过重新整理式(1)可以得到不存在虚假出价时的卖者期望收益: Ucom(x)=nF(x)n-1[1-F(x)]·w(x)+ (9) 将式(8)与式(9)相减,得到卖者参与虚假出价动机表达式: (F(2:n)(x)-F(1:n)(x))(b(x)-w(x))+ nF(x)n-1[1-F(x)]·[b(x)-w(x)]+ F(u)n-2f(u)du (10) 式中,竞拍者人数n为: n(s)= 这里参考MW[15]的分析方法,引入“拟收入的单峰性”假设(unimodality of the quasi-revenues)。与MW研究中一般对称模型的推导类似,设定两个“拟收入”函数假设。在独立私有价值假设下有w=v,此时的“拟收入”假设就与Myerson研究中的假设一致,即期望收益是保留价格的单峰函数。 假设1:(拟收入的单峰性)以下函数是严格拟凹的拟收入函数: R1=(F(2:n)(x)-F(1:n)(x))·w(x)+ (11) R2=(F(2:n)(x)-F(1:n)(x))·v(x)+ (12) 其中,x*为拟收入函数R1的解,r*=w(x*)为对应的保留价格。 由于第一价格拍卖的竞拍机制为价高者得,且支付金额为最高虚假出价,任何欺诈行为均会影响成交率进而降低期望收益。所以,第一价格拍卖中的均衡结果不会受到虚假出价影响。结合前述定理,得到定理2。 定理2:当信号分布独立且存在虚假出价时,均衡状态下,第一价格密封拍卖得到的收入高于第二价格密封拍卖,即: 由定理2可知,存在或不存在虚假出价时的第一价格密封拍卖下的最优保留价格会小于存在虚假出价时第二价格密封拍卖中的最优保留价格。因此,第二价格密封拍卖中的成交概率更低,应用第一价格密封拍卖均衡时的卖者期望收益更高,卖者在第一价格密封拍卖中的虚假出价动机更强烈。 (13) 为了更加清晰地了解当存在虚假出价时竞拍者人数以及拍品价值对卖者参与虚假出价动机的影响情况,这里对信号分布采用特殊形式的假设并进行数值分析。假设信号Xi独立且为[0,1]上的均匀分布,拍品估值是信号x的线性函数,即: 其中,α为竞拍者估值中个人估值占比,n为参与竞拍人数。沿用上文竞拍者估值的假设并结合卖者在存在虚假出价时的期望收益式(8)与不存在虚假出价时的期望收益式(9),分别计算出不同参数下的卖者期望收益取值,如表1所示。 表1 卖者期望收益的数值变化 可以看到,卖者参与虚假出价的动机是竞拍者人数n和个人估值占比α的减函数。此外,随着物品价值中个人估值占比α的增大,竞拍者估值中参考对手竞拍者出价信息的比例将减少,说明竞拍者仅依靠自身估值便可虚假出价,此时参与虚假出价所带来的卖者期望收益的增加也将减少,卖者的参与动机逐渐减弱。综合竞拍者人数和物品价值的数值分析结果来看,拍卖中的竞拍者人数越多、拍品估值中个人估值占比越高,竞拍者可获得的信息越多且仅依靠个人估值就可确定虚假出价,卖者参与虚假出价的动机就会越小。 (1)数据说明。 本次拍卖数据搜集源自淘宝网17个拍卖类别,包括20个拍卖子类的拍卖4 282个,共计出价96 106次。其中,7天期7个拍卖类(9个拍卖子类)包含3天、5天、7天和10天四个期限的拍卖,10个拍卖类(18个拍卖子类)仅含7天期拍卖。不同期限拍卖类样本选择情况见表2。 表2 不同期限拍卖类样本选择情况 (2)估计结果。 运用上述方法分别对20个拍卖子类的7天期拍卖数据进行了估计,相应的参数估计见表3。 卖者参与虚假出价得到的期望收益会高于不存在虚假出价时的期望收益,成为其参与虚假出价的主要动机。这里以艺术品类拍卖为例,分别绘制存在与不存在虚假出价时的卖者期望收益曲线,分析卖者参与虚假出价动机的阶段性变化特征。这里假设信号Xi独立且为[0,1]上的均匀分布,竞拍者估值是信号x的线性函数,即: 其中,α为竞拍者估值中个人估值占比,(1-α)则为估值中参考其他信息占比,n为参与竞拍人数。结合上文得到的艺术品类参数估计值和卖者的期望收益式(8)和式(9),分别绘制卖者在存在与不存在虚假出价时的期望收益阶段变化曲线,如图1所示。 图1 卖者期望收益阶段变化曲线 存在虚假出价时的卖者期望收益高于不存在虚假出价时的卖者期望收益,二者的差值是时间的减函数,即随着拍卖的进行,第一阶段二者差值最大,说明此阶段卖者参与虚假出价的动机最强烈,第二阶段二者差距逐渐缩小,在拍卖结束前趋于一致,意味着卖者参与虚假出价的动力随着拍卖的进行而不断减弱。这就解释了在现实拍卖中,卖者为了增加竞拍的激烈程度,通常偏向于在拍卖初期和中期参与虚假出价,增加拍卖的激烈程度从而吸引更多的诚实竞拍者出价,而在拍卖末期,为了避免赢标风险,多数卖者避免选择在拍卖末期参与虚假出价,即在参与虚假出价推高竞拍者出价以获取稍高的期望收益与卖者赢得拍品间权衡,多数卖者会选择不参与虚假出价而避免赢标带来的损失。 根据卖者期望收益阶段变化模型逐一绘制竞拍者人数从2(假设至少存在一名虚假出价者)至70变化时的卖者期望收益曲线。通过比较不同竞拍者人数下的卖者期望收益对应的最优保留价格可以看到,所有卖者期望收益曲线均存在两个峰值,当竞拍人数少于30人时,卖者期望收益曲线的第二个峰值高于第一个峰值,此时的卖者最优保留价格位于第二个峰值处,对应较高的卖者期望收益,说明卖者此时通过参与虚假出价将原有保留价格提高至最优保留价格便可获得更高的期望收益,即卖者存在参与虚假出价的动机;当竞拍人数超过30人时,卖者期望收益曲线的第一个峰值便会超过第二个峰值,卖者的最优保留价格位于第一个峰值处,说明卖者无法通过参与虚假出价修改保留价格以获得更高的期望收益,此时卖者的参与动机降低,卖者参与虚假出价的动机随着竞拍者人数的增加而减弱。下面分别选取了竞拍者人数n为2、35、61时的卖者期望收益随保留价格变化曲线,见图2~图4。 图2 n=2时卖者期望收益随保留价格变化曲线 图3 n=35时卖者期望收益随保留价格变化曲线 图4 n=61时卖者期望收益随保留价格变化曲线 得到20个拍卖子类下卖者期望收益随保留价格变化曲线,见图5。 图5 20个拍卖子类卖者期望收益随保留价格变化曲线 可以看到,尽管初始假设相同,20个拍卖子类中不同类拍品下的卖者期望收益与保留价格的变化却不尽相同。首先,通过比较纵轴可以看到,艺术品、收藏、珠宝类拍卖由于拍品单价较高,所获得的卖者期望收益普遍高于其他类拍品。其次,手表、收藏类、园艺类拍卖下,保留价格第一峰值对应的卖者期望收益高于第二峰值下的卖者期望收益,说明卖者在拍卖前期已设定好的保留价格在拍卖进行时并不会为追求更高期望收益而更改,即这几类拍卖中的卖者没有参与虚假出价的内在动力。再次,古董、书籍、照片、乐器类等拍卖中保留价格前后两个峰值对应的卖者期望收益值相近,在没有网站相关规则约束和监督下,卖者也许会考虑在拍卖进行中对保留价格进行更改以获得更高收益,但更改保留价格的内在动力并不充足。最后,对于艺术品、手机两类拍卖而言,保留价格第一峰值对应的卖者期望收益则低于第二峰值对应的卖者期望收益,说明卖者的期望收益会随着拍卖的进行、竞拍人数的增多而增加,卖者可以通过竞拍者的虚假出价行为逐渐了解其估值,此时卖者有更改最初保留价格以获得更高期望收益的内在动力,但由于大多数拍卖网站相关规则限制,一经设定的最初保留价格在拍卖开始后无法进行修改,卖者只能通过注册虚假账号或与他人虚假出价的方式参与竞拍,以达到改变初始保留价格、获得更高期望收益的目的。 进一步的,卖者参与虚假出价的动机与拍品价值中个人估值占比相关。竞拍者在参与竞拍手表、园艺、书籍、乐器等拍卖类别时,个人估值占比较高,仅根据自己的估值便可按真实估值虚假出价,该类拍卖下卖者的参与动机较弱。艺术品类别下的拍品具有非统一性、非实用性和非再生性等特征,这类拍品的价值往往是不确定的,所以竞拍者在参与艺术品类拍卖虚假出价估值不仅会依赖自身所拥有的信息,还会参考对手竞拍者的估值虚假出价信息,为卖者实施虚假出价提供了空间。 虚假出价对拍卖结果的影响在现有多数研究中被低估了。该文通过分析卖者参与动机随时间的变化情况以及受拍卖方式、关联程度、竞拍者人数和拍品价值的影响变化情况,得到以下结论并提出可操作性建议:(1)卖者参与虚假出价的动机来自于期望收益的变化,存在虚假出价时的卖者期望收益高于不存在虚假出价时的期望收益,二者的差值随拍卖的进行不断缩小,参与动机也相应减弱。(2)卖者在第二价格密封拍卖中的虚假出价动机更强烈,且关联程度越高,虚假出价动机也越大。(3)竞拍者人数的增加,并不会增强卖者参与虚假出价的动机。当竞拍者人数增加时,卖者最优保留价格对应的期望收益的增加则逐渐减少,卖者无法通过虚假出价获得较高的期望收益,参与虚假出价的动机减弱。(4)卖者的参与动机与拍品价值中个人估值占比相关。竞拍者在参与价值较为固定的拍卖类别时,仅根据自己的估值便可虚假出价,而较少参考其他竞拍者的虚假出价,该类别下的虚假出价动机较弱;当竞拍者参与价值不确定性较高的竞拍时,拍品价值中个人估值占比较小,多数竞拍者会参考对手竞拍者的估值虚假出价信息,卖者参与虚假出价的动机较强。 基于以上结论,拍卖平台可以选择适当延长拍卖时间、扩大宣传等方式畅通信息流通渠道,吸引更多的竞拍者参与竞拍,以减弱卖者参与虚假出价的动机。此外,拍卖平台还可以通过标注拍品估值、丰富详情描述等方式为竞拍者估值做参考,以减少竞拍过程中买卖双方信息不对称程度,有效抵御网络拍卖中虚假出价行为的发生。对于竞拍者而言,可以选择竞拍时间较长且参与人数较多的拍卖参与竞拍。在拍品类别的选择上,可以多选择价值较为固定且二手交易市场活跃的拍卖类别参与竞拍。而在参与艺术品等价值不确定性较高的拍品拍卖时,首先应提高自身的艺术素养并按个人真实估值虚假出价,最大限度地降低虚假出价对虚假出价的影响。1.2 虚假出价动机理论模型
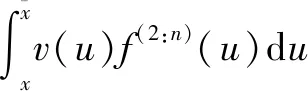
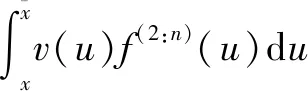

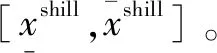



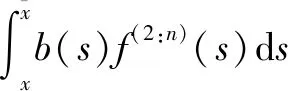

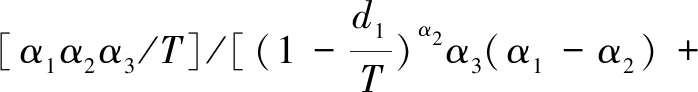


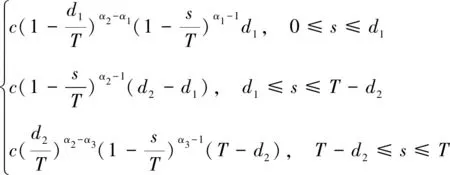
2 虚假出价动机的影响分析
2.1 拍卖方式
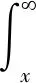
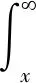



2.2 关联程度


2.3 拍品价值与竞拍者人数

3 实证分析与验证
3.1 模型参数估计

3.2 虚假出价动机阶段性变化的特征分析

3.3 竞拍者人数对虚假出价动机的影响分析



3.4 拍品类别对虚假出价动机的影响分析
4 结束语

