β衰变型自给能堆芯中子探测器灵敏度数学模型

于稼驷

（中华人民共和国生态环境部，北京 100006）

自给能探测器广泛用于连续监测大型核动力堆堆芯中子注量率水平及其分布；这种小型、全固化的探测器，耐辐照、易安装、寿命长，是一种较理想的堆芯中子注量率探测元件。

自给能中子探测器发射体吸收中子后，诱发β衰变，形成输出电流。我们把这类自给能中子探测器称为β衰变型中子探测器，主要包括铑、钒自给能探测器。

探测器灵敏度是自给能探测器的核心参数。国内外很多文献［1-5］探讨、分析、研究了铑、钒自给能探测器灵敏度的计算方法或数学模型。

要系统地刻度探测器的灵敏度是困难的，特别对铑探测器，不但要刻度热中子灵敏度，而且要刻度探测器灵敏度随堆芯中子谱超热参数的变化。因此，建立一个考虑了超热共振中子影响的探测器灵敏度数学模型是很有必要的。本文将介绍这样一个数学模型——铑探测器数学模型，并对未经燃耗的铑和钒探测器在轻水堆系统中的灵敏度作了计算，结果与实验值符合较好。钒探测器数学模型与铑探测器数学模型的热中子部分相同。

灵敏度是本论文的核心概念，为了便于论述，现定义两个术语：（1）探测器灵敏度，即整个探测器单位中子注量率输出电流；（2）探测器单位长发射体灵敏度，是与单位长（1 cm，下同）发射体相对应的那部分探测器灵敏度的简称。如果探测器灵敏度为I，探测器发射体长度为L，那么探测器单位长发射体灵敏度为I/L。

1 铑探测器灵敏度数学模型

铑探测器放在稳定典型热堆中子场中，在平衡状态下，发射体单位时间放出的β粒子数等于其俘获的中子数。发射体放出的β粒子在穿越发射体过程中损失能量，以一定的概率逃脱发射体，我们把逃脱到发射体表面的β粒子能量分布称为逃脱谱。逃脱发射体的β粒子，只有穿越绝缘区空间电荷电势峰才能对探测器灵敏度有贡献。因此，我们分以下四部分逐步分析，最后建立数学模型。

1.1 发射体中子俘获率

103Rh 的中子吸收截面在热中子区近似附合1/v律，在超热区中子能量为1.26 ev 处有一个峰值截面高达近4500 靶的强共振峰，且仅有这一个强共振峰，如图1 所示［6］。

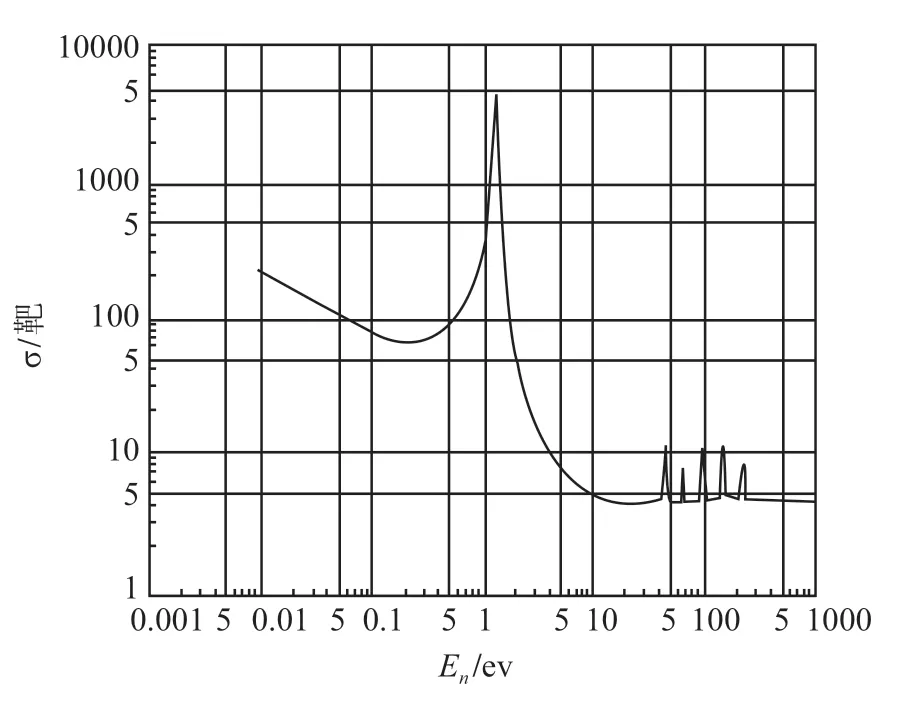
图1 103Rh 中子吸收截面随中子能量的变化Fig.1 Variation of neutron absorption cross section of103Rh with neutron energy

1.1.1 无限细铑丝中子俘获率

把一根无限细的铑丝，放入充分慢化的典型热堆中子场，单位长铑丝的中子俘获率可用以下公式计算。

（1）精准理论公式：

（2）简化近似公式：

文献［7］和文献［8］发展了一个公式（1）的简化近似公式［7，8］：

式（3）中，nv0为Westcott 中子注量率，其中n为总中子密度，v0=2200 米/秒；σ0为103Rh 热中子（2200 m/s）微观吸收截面；g、s为103Rh 的Westcott因子；N极细为单位长铑丝103Rh的核数；n（v）为速度为v的中子的密度；σ（v）为103Rh 速度为v的中子的微观吸收截面；v为中子速度；r为中子谱超热指数，简称超热指数，是中子谱超热中子比例的量度，可以用镉比法进行测量。σ有效为103Rh 有效吸收截面，其物理内涵见式（3）。

（3）替代公式：

其中，T为中子温度；T0= 20℃（293.15 K）；为中子谱超热参数（以下简称超热参数）；s0=s（20℃），其他同上。

本文附录一通过数据详细分析、论证了用式（4）替代式（3）的合理性、可行性。附录一分析表明，用式（4）替代式（3）计算103Rh 的有效截面，引起的误差是很小的，相对误差小于1%。该替代公式为本文数学模型的建立创造了条件、奠定了基础。

把式（4）代入式（2），可得：

如果把上述极细铑丝放入一个纯的热中子谱中，如反射层中，此时r= 0，那么，单位长铑丝的热中子俘获率为A极细1。因此，A极细1代表了热中子的贡献；A极细2代表了超热中子的贡献。由于：（1）103Rh 的中子吸收截面在超热区中子能量为1.26 eV 处有一个峰值截面高达4500 靶的强共振峰；（2）典型热堆的中子注量率在超热慢化区的能谱分布符合1/E 律；（3）图1 表明，在超热区，103Rh 的中子吸收截面在共振区以外的区域都很低；因此，A极细2主要代表超热共振中子的贡献。

1.1.2 探测器发射体的中子俘获率

由于铑自给能探测器发射体不是无限细的，计算单位长铑发射体的中子俘获率时需要进行中子注量率降低和中子自屏蔽修正。计算单位长铑发射体的中子俘获率的修正公式如下：

其中，N1为单位长发射体103Rh 的核数；f1为发射体热中子自屏因子；F1为发射体热中子注量率降低因子；f2为发射体超热共振中子自屏因子；F2为发射体超热共振中子注量率降低因子，其他同上。

1.2 探测器单位长发射体灵敏度计算简化公式及探测器灵敏度刻度结果

1.2.1 探测器单位长发射体灵敏度计算简化公式

在平衡状态下，发射体单位时间放出的β粒子数等于其俘获的中子数。但β粒子只有逃脱发射体，并穿越绝缘区空间电荷电势峰才能对探测器灵敏度有贡献。那么探测器与单位长发射体、单位中子注量率相对应的输出电流，即探测器单位长发射体灵敏度，可用下式表示：

其中，e为电子电量；K热β有效为热中子诱发的β粒子逃脱发射体并穿越绝缘区空间电荷电势峰的概率；K超振β有效为超热中子，主要是共振中子诱发的β粒子逃脱发射体并穿越绝缘区空间电荷电势峰的概率；re为发射体半径；N为单位体积发射体103Rh 的核子数；等同于式（6）中的N1，其他同上。

发射体热中子自屏因子f1和热中子注量率降低因子F1引自文献［9］；超热共振中子自屏因子f2引自文献［10］［9，10］。

文献［9］中的中子注量率降低因子适用于多能中子系统，当然也适用于103Rh 共振峰区间的中子。由于发射体对103Rh 的大多数共振中子（尤其是共振峰半宽度内的中子）可以近似看成黑体，满足了文献［9］中x（Σare）值远大于1 的条件，即文献［9］中的式（6）可简化成式（7）。这样大多数共振中子的中子注量率降低因子与发射体的宏观吸收截面无关，而只与发射体的半径和共振中子在探测器周围介质中的扩散长度及迁移平均自由程有关。因此，我们用1.26 eV 中子的中子注量率降低因子近似代替共振峰区间中子的中子注量率降低因子的平均值，引起的误差是不大的。

式（8）表明，探测器单位长发射体灵敏度将随着超热参数的变化线性变化。

1.2.2 探测器灵敏度刻度结果

文献［11］、［12］介绍了铑探测器灵敏度随超热参数变化的刻度结果，如图2、图3 所示：

图2 铑探测器灵敏度随超热参数的变化Fig.2 Variation of sensitivity of Rh detector with epithermal parameters

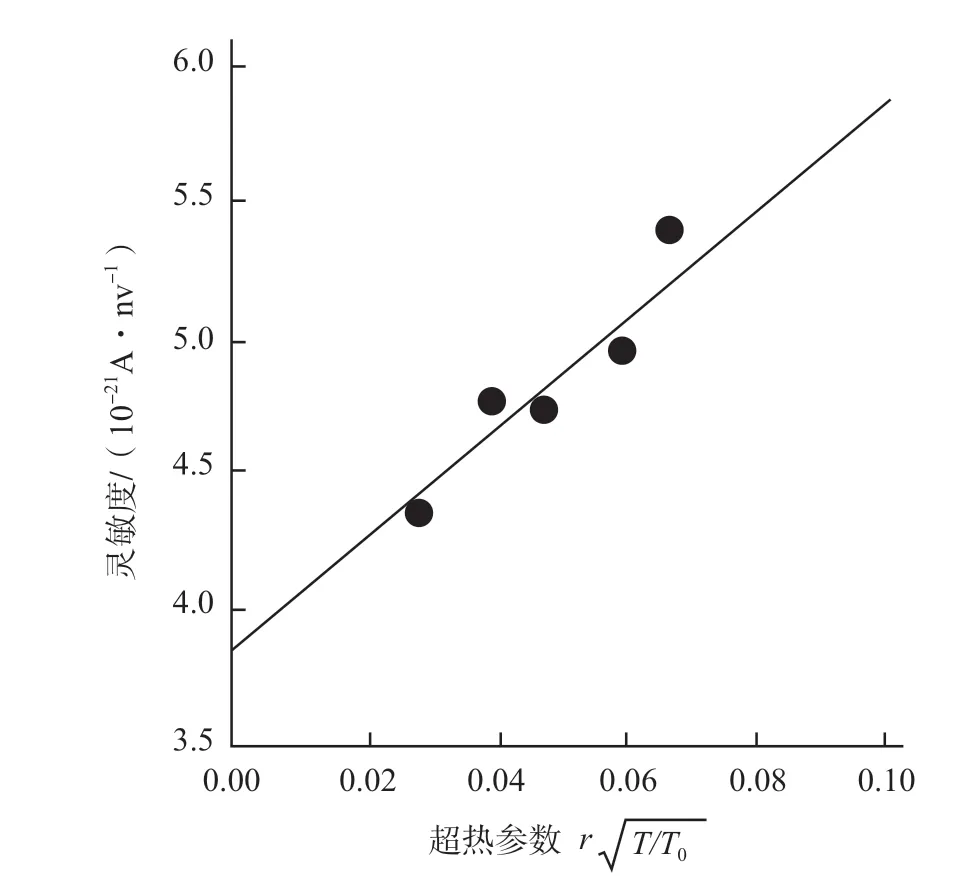
图3 铑探测器灵敏度随超热参数的变化Fig.3 Variation of sensitivity of Rh detector with epithermal parameters

图2 来自参考文献［11］。探测器发射体直径为0.5 mm、长度为30 mm。探测器灵敏度可用下式表示：

由式（9）可算得，超热参数从0 增加到0.1，该探测器的灵敏度增加36%。

图3 来自参考文献［12］。探测器发射体直径为1 mm、长度为20 mm。探测器灵敏度可用下式表示：

式（10）中的误差为最小二乘法的标准误差。从此式可算得，超热参数从0 增加到0.1，该探测器的灵敏度增加54%。

图2 和图3 中，为了简化灵敏度单位的表达式，用nv 表示单位中子注量率［n·（cm2sec.）-1］，下同。

在推导公式（8）的过程中，笔者做了许多推理性假定，如超热中子对中子俘获率的贡献主要是来自共振中子的贡献，以及用共振中子的自屏因子、中子注量率降低因子代表超热区的自屏、中子注量率降低效应等。公式（8）表明，铑探测器单位长发射体灵敏度是随超热参数线性变化的。铑探测器灵敏度刻度结果也表明，其灵敏度是随着超热参数线性变化的。因此可以说，式（8）描述的物理现象与实验结果是一致的。

1.3 β粒子逃脱谱

现在我们讨论β粒子穿越发射体过程中的能量损失和β粒子逃脱谱（βparticle escape energy spectrum）。

热中子（2200 m/s）在103Rh 里的平均自由程约为0.1 cm，我们可假定热中子在发射体内均匀吸收，从而β粒子也均匀产生，且各向同性发射。能量为1.26 eV 的共振中子在103Rh 里的平均自由程约为0.003 cm。我们可假定共振中子只在发射体表面吸收，从而β粒子只在发射体表面均匀产生，且各向同性发射。我们还假定β粒子在发射体里的穿越径迹为直线。

1.3.1 热逃脱谱

铑发射体吸收热中子后放出的β粒子逃离发射体表面时的能量分布叫热逃脱谱。换句话说，热逃脱谱是指这些β粒子穿越发射体，到达发射体表面，但还没有离开表面时的能量分布。从文献［1］知，热逃脱谱可用下式表示：

其中，l为径迹长度；；L为发射体长度；re为发射体半径；E（k）、K（k）分别为第一类、第二类完全的椭圆积分。

1.3.2 超热共振逃脱谱

铑发射体吸收超热共振中子后放出的β粒子逃脱到发射体表面时的能量分布叫超热共振逃脱谱。换句话说，超热共振逃脱谱是指这些β粒子穿越发射体，到达发射体表面，但还没有离开表面时的能量分布。吸收超热共振中子后放出的β粒子半数不穿经发射体直接逃脱，即不损失能量直接贡献给逃脱谱。用文献［1］分析热逃脱谱类似的方法分析超热共振逃脱谱，超热共振逃脱谱可用下式表示：

其中，N2［R（E'） -R（E）］为柱体表面均匀、各向同性源径迹长度概率函数，以下用N2（l）表示；其他符号同上。

在附录二中，用文献［13］中推导N1（l）相似的方法推导出了N2（l）：

1.4 穿越电势峰概率

由于探测器绝缘体内杂质及晶格缺陷的存在，在堆芯强辐射场，绝缘体将捕获一些电子，形成绝缘体空间电荷。在通常工作状态下，绝缘体内空间电荷电势分布［1，14］如下：

其中，ρ0为绝缘体捕获的电子的电荷密度；ε为陶瓷绝缘体介电常数；k=re/ri；ri为绝缘体外半径；re为发射体半径；r为绝缘体内任一点到发射体轴线的距离。

绝缘体空间电荷电势峰面半径为：

逃脱发射体的β粒子，只有穿越空间电荷电势峰才对灵敏度有贡献，否则将在空间电荷电场作用下漂移回到发射体。假定：逃脱到发射体表面的β粒子从发射体表面各向同性发射，在绝缘体里穿越径迹为直线。设一个到达发射体表面能量为E 的β粒子在绝缘体中的射程为R（E），以发射体表面任一点为球心，以R（E）为半径做一个半球，半球的底面与发射体表面相切。我们近似地把该半球的球表面在电势峰面以外部分与整个半球的球表面面积之比，作为该β粒子穿越空间电荷电势峰概率。在发射体表面能量为E 的β粒子穿越电势峰概率用P（E）表示：

1.5 数学模型

由式（6）和式（7）可知，探测器单位中子注量率、单位长发射体中子俘获率为：

如上所述，其中A1为热中子俘获率，A2主要代表超热共振中子俘获率。

发射体每俘获一个热中子在发射体表面出现一个能量为的β粒子的概率为C1（E）；发射体每吸收一个超热共振中子在发射体表面出现一个能量为E的β粒子的概率为C2（E），那么，对于单位中子注量率，在单位时间内，单位长发射体表面出现能量为E 的β粒子数为：

发射体表面β粒子逃脱谱中能量为E的β粒子穿越绝缘体空间电荷电势峰概率为P（E），那么探测器单位长发射体灵敏度为：

其中，e为电子电量；E0为穿越（r0-re）厚绝缘体所需β粒子能量。

式（20）还可以用下式表示：

2 铑探测器轻水堆单位长发射体灵敏度计算结果

2.1 铑探测器单位长发射体热中子灵敏度，见表1、图4

表1 ≈s（20℃）分析

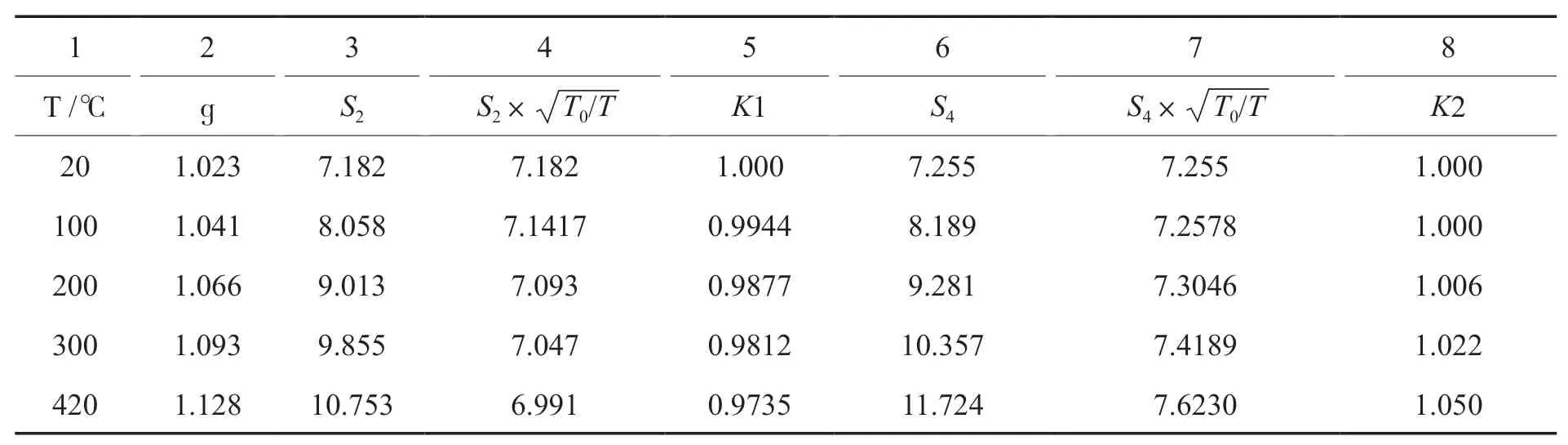
表1 ≈s（20℃）分析

注：表中，第一列、第二列、第三列、第六列的数据引自参考文献［8］的表1。

1 2 3 4 5 6 7 8 T /℃gS2S2× T0/TK1S4S4× T0/TK2 201.0237.1827.1821.0007.2557.2551.000 1001.0418.0587.14170.99448.1897.25781.000 2001.0669.0137.0930.98779.2817.30461.006 3001.0939.8557.0470.981210.3577.41891.022 4201.12810.7536.9910.973511.7247.62301.050

表1 铑探测器单位长发射体热中子灵敏度a 值Table 1 Thermal neutron sensitivity a value of unit length emitter of Rh detector单位：10-21 A·（nv·cm）-1

图4 铑探测器单位长发射体热中子灵敏度随发射体半径（re）及绝缘体厚度（ri-re）的变化Fig.4 Variation of thermal neutron sensitivity per unit length emitter of Rh detector with emitter radius（re）and insulator thickness（ri-re）

2.2 铑探测器单位长发射体超热共振b 值（见表2、图5）

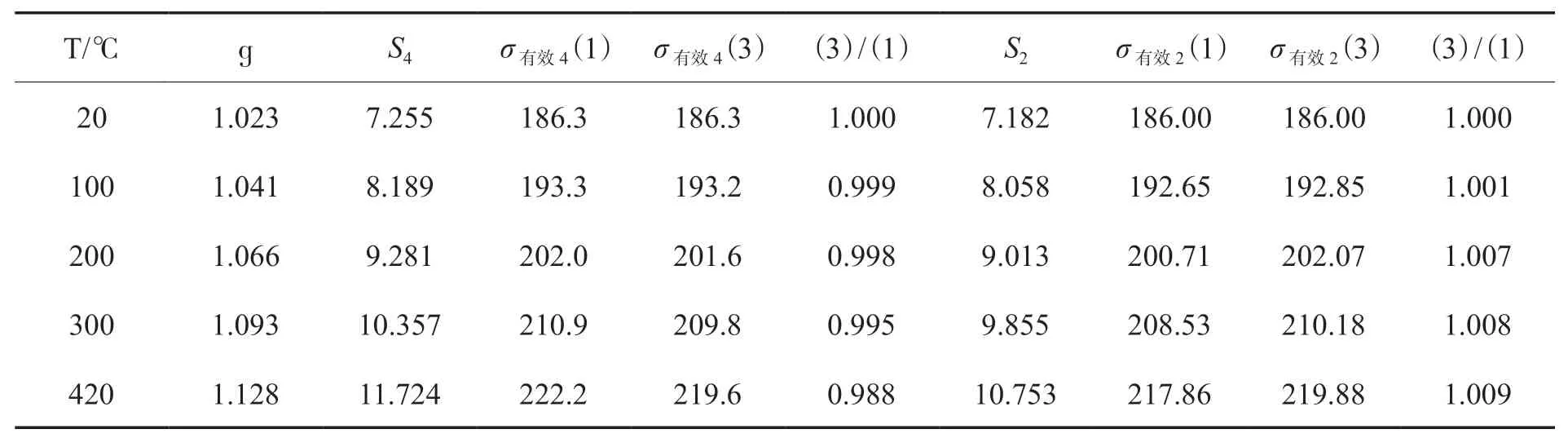
表2 有效截面σ有效4、σ有效2 计算结果比较（r =0.03）Table 2 Comparison of calculation results of effective cross sections σeffective-4 and σeffective-2

表2 铑探测器单位长发射体超热共振b 值Table 2 Epi-thermal resonance b value per unit length emitter of Rh detector单位：10-21 A·（nv·cm）-1

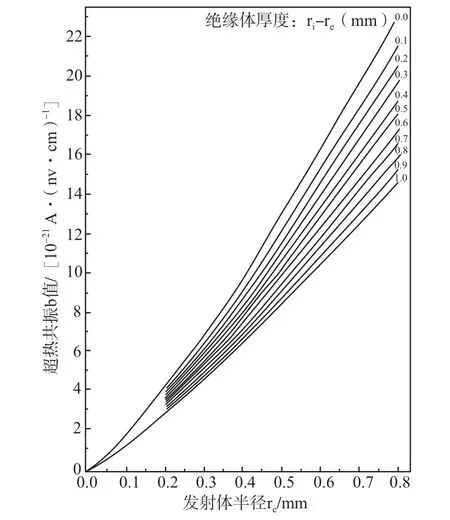
图5 铑探测器单位长发射体超热共振 b 值随发射体半径（re）及绝缘体厚度（ri-re）的变化Fig.5 Variation of epi-thermal resonance b value per unit length emitter of Rh detector with emitter radius（re）and insulator thickness（ri-re）

3 钒探测器轻水堆灵敏度数学模型及计算结果

钒探测器灵敏度数学模型与铑探测器灵敏度数学模型的热中子部分相同。钒探测器与单位长发射体、单位中子注量率对应的输出电流，即探测器单位长发射体灵敏度，可用下式表示：

式（23）中，为钒探测器发射体热中子自屏因子，F为钒探测器发射体热中子中子注量率降低因子，其他同上。

3.1 钒探测器单位长发射体热中子灵敏度，见表3、图6

表3 钒探测器单位长发射体热中子灵敏度Table 3 Thermal neutron sensitivity of unit length emitter of V detector单位：10-21 A·（nv·cm）-1

图6 钒探测器单位长发射体热中子灵敏度随发射体半径（re）及绝缘体厚度（ri-re）的变化Fig.6 Variation of thermal neutron sensitivity per unit length emitter of V detector with emitter radius（re） and insulator thickness（ri-re）

4 计算结果数据分析

4.1 铑探测器单位长发射体热中子灵敏度a 值

灵敏度计算模型中，假定热中子在发射体内均匀吸收，β粒子在发射体内均匀、各向同性发射。发射体体积与发射体半径re的平方成正比，因此，发射体单位长度内103Rh 的核子数也与其半径re的平方成正比。从图4 可以看出，re＜0.3 mm 时，铑探测器单位长发射体灵敏度与re近似成正比；re＞0.3 mm 时，re越大，灵敏度增长越缓慢，这是因为re越大，热中子的自屏效应、中子注量率降低效应越强，且β粒子逃脱发射体越困难，即K热β有效越小。

4.2 铑探测器单位长发射体超热共振b 值

在灵敏度计算模型中，笔者假定超热共振中子在发射体表面均匀吸收；β粒子在发射体表面均匀、各向同性发射。发射体表面积与re成正比。从图5 可以看出，铑探测器单位长度超热共振b 值与re近似成正比。超热共振中子在发射体表面吸收，β粒子在发射体表面发射，因此有一半β粒子直接逃脱发射体，这可能是超热共振b 值与re近似成正比的合理解释。

4.3 钒探测器单位长发射体热中子灵敏度

钒的中子吸收截面较好地符合1/v规律，且比铑的吸收截面小得多，因此其发射体的热中子的自屏效应、中子注量率降低效应与铑相比要弱。再者，钒的密度低，约是铑的密度的50%，因此，β粒子从钒发射体中逃脱相对容易，即K热β有效相对较大。从图6 可以看出，钒探测器单位长发射体热中子灵敏度与re近似成正比，并没有像铑探测器那样——re越大，灵敏度增长越缓慢的现象，这应该是合理的。

5 探测器单位长发射体灵敏度计算结果与实验结果的比较及误差分析

表4 给出了计算结果与实验结果的比较，刻度数据（即实验值）引自参考文献［1］、［11］、［12］。刻度探测器发射体长度在表中给出，而计算中都取2 cm（指径迹长度概率函数中，发射体长度L=2 cm）。第4、5 号探测器绝缘体为氧化镁（MgO），其他为三氧化二铝（Al2O3），而计算中仅考虑了Al2O3。［1，11，12］

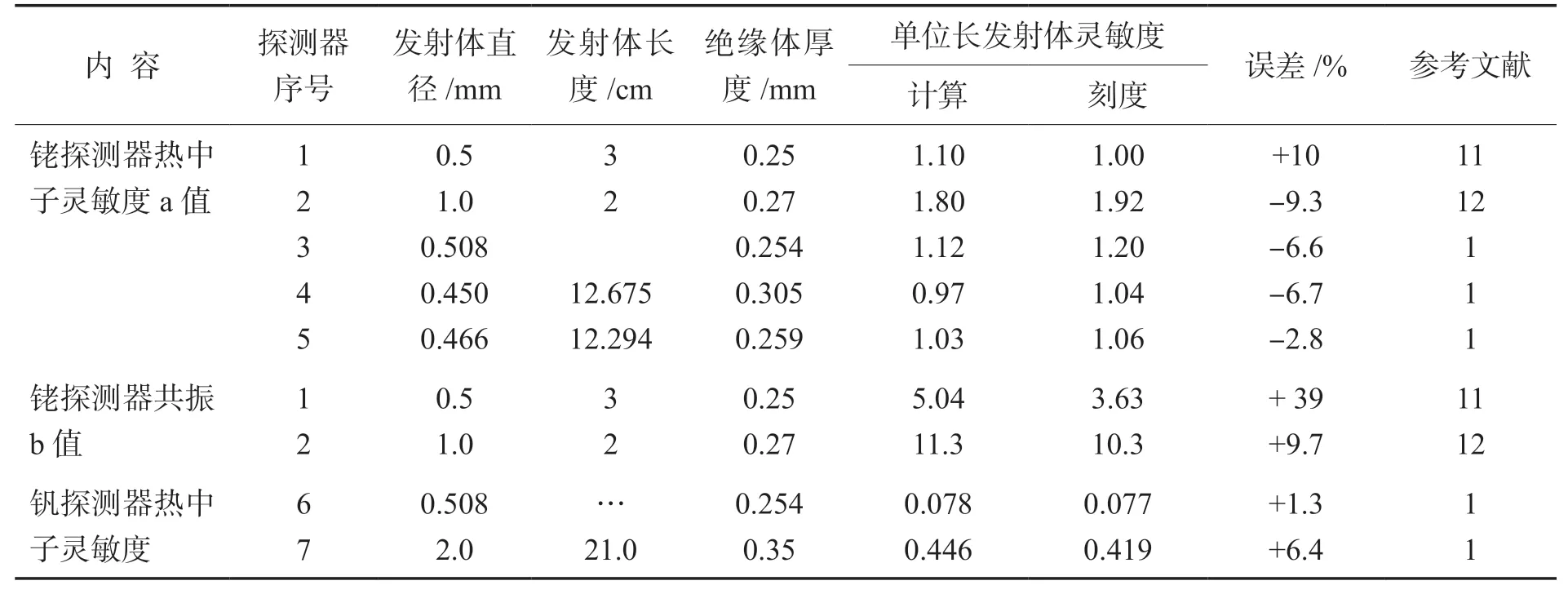
表4 探测器单位长发射体灵敏度计算结果与实验结果的比较Table 4 Comparison between calculated results and experimental results of unit length emitter sensitivity of detector单位：10-21 A·（nv·cm）-1

表4 中给出的计算数据与刻度数据都是探测器的单位长发射体灵敏度数据。文献［1］中表4 直接给出了铑、钒探测器单位长发射体灵敏度的刻度结果，这里直接引用。文献 ［11］、［12］ 给出的是铑探测器灵敏度刻度结果，即整个探测器的灵敏度（见本文1.2.2节）的刻度结果。表4 中已经换算成探测器单位长发射体灵敏度的刻度结果，即铑探测器单位长发射体热中子灵敏度a 值的刻度结果，以及铑探测器单位长发射体共振b 值的刻度结果。

从表4 可以看出，结果较满意，说明该模型是可取的。计算结果比实验结果小是合理的，因计算中没考虑γ 射线诱发的瞬发β粒子对灵敏度的贡献，这些瞬发β粒子所致灵敏度约占总灵敏度的5%～10%［13］。

产生误差的原因是多方面的：计算铑丝在典型热堆中子场中的中子俘获率的公式是一个近似公式；计算值基于轻水堆、中子温度20℃，而刻度值有的基于重水堆，中子温度未知；许多“因子”的取值有一定误差；建立数学模型过程中做了许多假定；计算中允许的计算误差；实验值也有一定的测量误差；再加上计算中没考虑γ 射线诱发的瞬发β粒子对灵敏度的贡献等。

表4 中，发射体直径为0.5 mm 的探测器的共振b 值，其理论计算值以轻水堆为背景，刻度值以重水堆为背景。本文式（8）表明，共振b 值=eK超振β有效f2F2πr2eNσ0s0。该短式中，只有f2F2因子组合和堆型有关，其他因子或参数都与堆型无关。因此，若理论计算值以重水堆为背景，本文式（8）中的f2F2因子组合，约是以轻水堆为背景的f2F2因子组合的1.044 倍。据此可推算出，若理论计算值以重水堆为背景，误差约为+45%。

6 联想

G. Knill 先生于1968 年发表的论文［11］描述了发射体直径为0.5 mm 的铑探测器灵敏度随超热参数线性变化的规律（图2），但论文并没有对这一“线性规律”给出解释。虽然论文中在解读这一曲线时说：“Also from this graph a value of 3.46 can be deduced for，which describe the departure of 0.5 mm diameter Rhodium from a 1/v characteristic。”笔者认为，这一段话的物理内涵不清晰，至今也未见其他论文对这一“典型线性变化”规律给出合理解释。

当铑探测器的几何尺寸及周围慢化剂确定后，本文式（7）、式（8）中，除外，其他参数都是常数，因此，铑探测器输出电流将随着线性变化。

因此也可以说，本文建立的理论，对这一“线性变化”规律给出了科学、合理的解释。

7 结论

（1）本文介绍的模型不仅能计算铑探测器热中子灵敏度，还能分析计算超热共振中子对铑探测器灵敏度的贡献。

（2）本文表4 给出了计算结果与实验结果的比较，结果令人比较满意，说明本文模型是科学、可行的。

（3）本文计算逃脱到发射体表面的β粒子穿越绝缘体空间电荷电势峰概率的方法及技术路线与Warren 模型不同［1］。本文的技术路线更直观、更好地反映了物理本征，计算结果应该更准确。

8 结语

本文计算以轻水堆为对象、设定中子温度为20℃，设定103Rh 的g= 1.023，s0=s（20℃） =7.255，设定Al2O3的密度为3.2 g·cm-3，103Rh 的共振峰值截面按4500 靶考虑，其他数据取常规数据。

感谢清华大学林翠琴教授、陈教授在推导柱体表面均匀、各向同性面源径迹长度概率函数中给予的指导帮助，感谢北京大学程檀生、陈鹤琴教授的支持帮助，感谢于岚的支持帮助。

附录一 103Rh 有效中子吸收截面替代公式及其可行性、合理性分析

把一个无限细的铑丝放在充分慢化的典型热堆中子场中，根据参考文献［7］、［8］，铑核素的有效吸收截面可用下式近似表示。

其中，r为超热指数，g、s为铑的westcott 因子。

上述公式（1），可改写为：

经过对参考文献［8］表1 中的103Rh 核素数据进行分析发现，公式（2）中的可以用表1 中的s（T0）即s（20℃）替代，即≈s（20℃），详见表1。这样公式（2）可以用下式近似：

其中，T为中子温度；T0= 20℃（293.1 K）；为超热参数；s（20℃）为中子温度20℃对应的铑的s值，即数学模型中的s0，其他同上。

用式（1）和式（3）分别计算103Rh 在不同中子温度下的热中子σ有效，结果见表2。

Table 1Analysis abouts≈s（20℃）

表2 中：σ有效4（1）表示用式（1）计算的σ有效4；σ有效4（3）表示用式（3）计算的σ有效4。同样σ有效2（1）表示用式 （1）计算的σ有效2；σ有效2（3）表示用式（3）计算的σ有效2。

计算σ有效4、σ有效2时，输入数据如下：σ2200（Rh） = 150.19 靶；r=0.03；T0= 20℃（293.15 K）。

由表2 可知，在中子温度＜400℃时，用式（3）替代式（1）计算103Rh 的有效截面，引起的误差是很小的，大都小于1%。这表明，在中子温度＜400℃时，用式（3）替代式（1）计算103Rh 有效截面是可以接受的。

由文献［8］可知，典型热中子堆，T/Tm＜1.07（Tm为慢化剂温度）。由此可以推断出，游泳池式研究堆的中子温度都小于100℃，而核电厂动力堆的中子温度小于400℃。因此从应用环境来讲，上述替代应用也是可行的。

附录二 柱体表面均匀、各向同性源径迹长度概率函数N2（l）

用文献［11］推导N1（l）相似的方法推导N2（l）。设一个半径为re、长度为L的柱体V，L＞＞re，如下图所示。在V 的表面均匀分布各向同性放射源。单位时间、单位面积放出的射线数为C，射线在V 内直线穿透。因有一半射线不穿经V，单位时间内，穿越V 的射线数（径迹数）为：。这里s为柱体的表面积，s= 2πre（re+L）。设将V 向-Ω→方向移动l距离得V'。V 在V'内的表面积为Sc。再将V 向-Ω→方向移动dl，s的改变量为dl。dsc内向Ω→方向发射的射线在V 内的径迹长度为l～（l+dl）。dsc面积元内单位时间发射的射线数为Cdsc=。

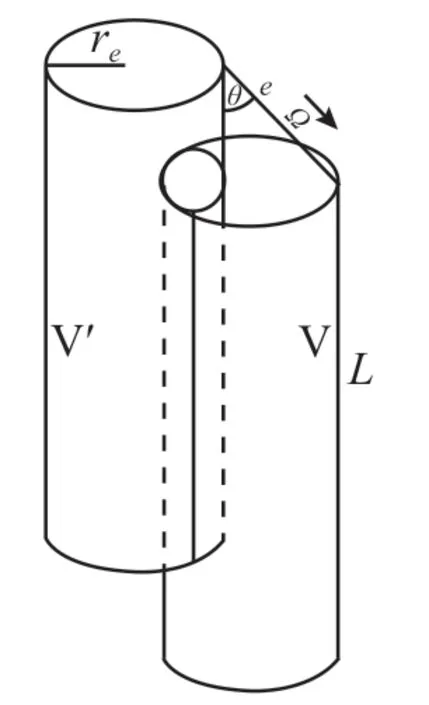
发射体(长度L,半径re)

这些射线中向Ω→方向单位立体角内发射的射线数为dl，而向Ω→方向单元立体角dΩ内发射的射线数为。从柱体V 表面单位时间发射出的射线穿经柱体V，在V 内径迹长度在l～（l+dl）的径迹总数为，单位时间穿越柱体V 的射线总数（总径迹数）为sc，那么，柱体表面均匀、各向同性源径迹长度概率函数为：

附录二中式（1）可变换成正文中式（12）。