移动式反应堆在不同公路等级下运输振动响应特性分析

凡天娣，张 勇，杨国威，宋 勇，蒋洁琼，周 涛

（1. 中国科学院合肥物质科学研究院，合肥 230031；2. 中国科学技术大学，合肥 230026；3. 中子科学国际研究院，青岛 266041）

移动式反应堆因其设计紧凑、固有安全性高、使用场景灵活多变等特点，不仅能为偏远岛屿实现供能，也能为国防提供安全保障，是当下研究的热点。如美国西屋研发的微型堆—伊达芬奇（eVinci），DOE 战略能力办公室的Pele 计划等［1-4］。目前我国的凤麟核团队正在开展这方面的研究［5，6］。移动式反应堆中的铅铋冷却剂具有密度高、质量大、体积小等特点，使得反应堆在车载上的质量分布不均。这与普通的大型设备的道路运输存在较大差异［7］。此外，道路运输下的车辆-道路激励是复杂多自由度的振动系统，路谱激励由路面传递到车身和设备上是一项复杂的过程，需经过系统耦合、振动传递和消减。因此，建立合适的车辆耦合模型是进行道路运输减振问题的重要研究手段。

在车辆建模方面，两个自由度的1/4 车体模型早在20 世纪30 年代已建立。随后在20 世纪50 年代，1/2 整车模型被建立，此时的模型能够体现车身的垂直振动和纵向角振动。20 世纪80 年代，学者们开始进行多自由度车辆模型研究，分析运输车辆的垂向振动响应、纵向及横向的角振动，建立全车的三维模型［8］。Okada等人建立了7 自由度下的全车模型包括用来描述车辆设计初期的操纵仿真［9］。Alkhatib R［10］等人采用遗传算法优化了悬架参数，对悬架系统的位移与车身加速度之间的关系进行求解。Tamboli［11］等人建立了两个自由度的1/2全车模型，研究随机路面激励下的系统振动响应规律。在对道路运输下的车辆运输问题上，现有研究多是分析车辆系统中的悬架设计、包装材料和减振设计等。对于车辆上装设备的安全特性分析也多拘泥在设备及运输车的减振上［12，13］。大多数研究中所建立的传统式车辆模型多是将车身和车载设备视为一个整体，但这样的模型无法精准地反应车载核电源上反应堆容器处的振动响应情况［14，15］。在核设备进行运输中，研究多集中在如何进行包装物的减振设计上［16，17］，少有研究反应堆容器在运输过程中所受路面不平度的激励的振动特性。

本文采用Lagrange 多体系统动力学方法建立分离式质量下全车振动的模型，在反应堆设备处安装三个减振器以观察其六个方向的振动响应。并对反应堆在不同装载质量及不同等级公路激励下的振动响应特性进行研究，得出移动式反应堆在不同等级公路运输下的振动响应。所得结论可为车载式移动反应堆在不同等级公路的工程运输过程研究提供参考。

1 公路运输下的整车系统模型

运输车辆连接了车辆与道路，并将道路不平度引起的路面激励从道路表面传递至车体，从而引起车载移动式反应堆的振动。本文对真实车辆模型进行适当简化，整车系统视为由质量-弹簧-阻尼组成的多体动力学模型。所研究的运输车辆为12×6 轴轮式自行车辆［14］，如图1 所示。将车载反应堆与车辆视为刚性连接，将12 个车轮看作独立的质量块。车辆上端通过车架弹簧与反应堆相连，下端轮胎与路面也通过弹簧相连，如图2 所示。

图1 运输车辆模型Fig. 1 Transport vehicle model

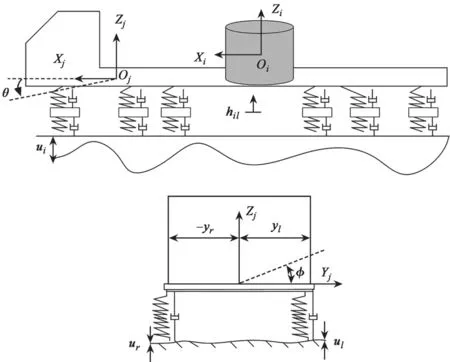
图2 运输车辆模型的坐标系统Fig.2 Coordinate system of transport vehicle model

2 路谱下整车多体动力学仿真模型

本文旨在研究移动式反应堆处的运输振动响应，因此考虑在车载反应堆设备与车体之间三个方向（X/Y/Z）上加装三个减振器（K5，K6，K7）以观察反应堆的六个自由度。区别于传统集中式质量模型，本文将整车系统简化为21 个自由度的动力学模型，主要包括车轮的12 个垂直自由度；车体上的3 个自由度：垂向方向的振动、俯仰和倾侧，设备的6 个自由度：垂直、俯仰和倾侧和绕三个坐标轴的转动。建立的全车仿真模型如图3 所示，系统模型中的参数及模型数据见表1 和表2［14］。

表1 系统的动力学模型符号表Table 1 Symbols of the dynamic model system

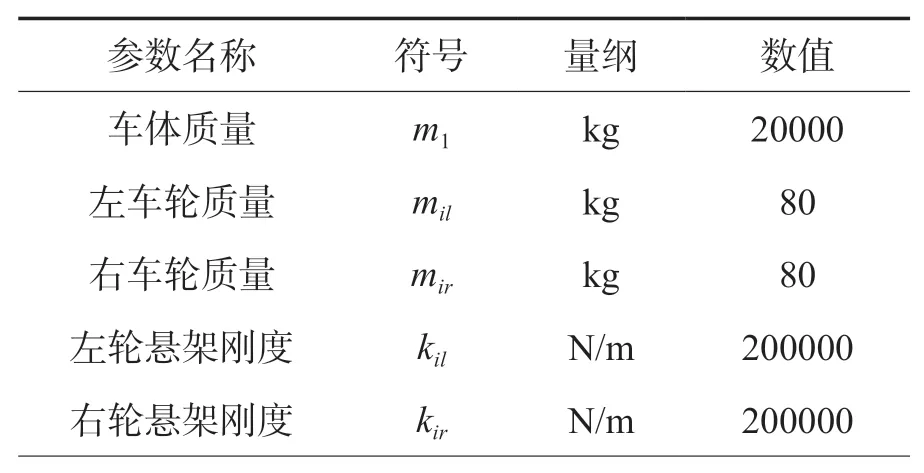
表2 系统的动力学模型参数表Table 2 Parameters of the dynamic system

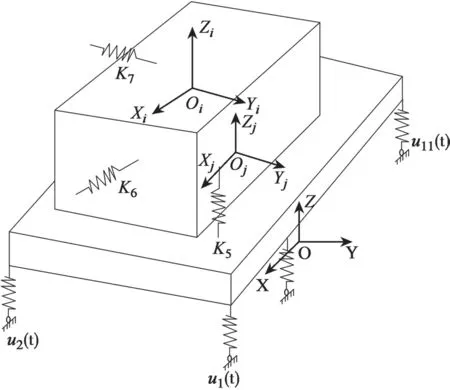
图3 分离式质量下车体系统的动力学模型Fig.3 Dynamic model under separated mass

2.1 全车系统的动能

总动能T由三部分组成：车体动能T1、设备动能T2和轮胎的动能T3。如图3 所示，假设车载设备材料构成相同且质量分布均匀，将其视为一个规则的几何体。可求得各部分的动能如下：

（1）车体的动能T1

假设车体的质心为Oj（xoj，yoj，zoj），φx为车体的前后俯仰位移，φy为左右倾侧位移，车体的动能表达式为：

式中，J1x是车体绕X 轴转动惯量，J1y是车体绕Y 轴转动惯量。

（2）车载设备的动能T2

令车载设备质心为Oi（xoi，yoi，zoi），绕OX 轴、OY 轴、OZ 轴旋转的转角分别为θx，θy，θz，则车载设备的动能为：

式中，J2x是车载设备绕X 轴转动惯量，J2y是车载设备绕Y 轴转动惯量，J2z是车载设备绕Z 轴转动惯量。

（3）轮胎的动能T3

则系统的总动能为：

2.2 全车系统的总势能

全车的总势能由12 个悬架弹簧、轮胎、车载设备上的3 个减振器弹簧的变形势能组成。三个减振器k5，k6，k7为分别连接车体与设备的竖直、水平前后、水平左右方向的弹簧，初始长度分别为l5，l6，l7。

（1）反应堆设备势能的计算

以在反应堆设备和车体的垂直方向为例，具体的连接形式见图4。C 点为连接车体上部中心（在OjXjYjZj中的位置向量为uCj），D 为连接设备的底部中心处（在OiXiYiZi中的位置向量为uDi），则：

图4 反应堆设备和车体的垂直方向处减振器连接Fig.4 The spring connect the reactor and the vehicle in vertical

系统运动后，Oi（设备质心）点在惯性坐标系OXYZ 中的位置向量为Roi，Oj（车体质心）点在惯性坐标系OXYZ 中的位置向量为Roj：

C 点和D 点在惯性坐标系OXYZ 中的位置向量为rC，rD：

弹簧k5变形后得长度Δl5为：

同理可求得车体与车载设备之间的前后水平方向的变化Δl6和左右水平方向的变化Δl7。

则设备的势能V3的表达式为：

车体的势能V1计算：

式中，（xil，yil，zil）为车轮的坐标（i=1…6）。

车轮的势能V2计算：

则系统总势能V为：

2.3 全车系统的振动方程

本文采用四阶Runge-Kutta 对微分方程进行求解。所建立的21 自由度全车振动方程为：

式中，X是系统位移，M是21×21 维质量矩阵，K是21×21 维刚度矩阵，Q是21×1 维激励系数矩阵，路面不平度施加在系统上的激励向量U为：

本文采用比例阻尼法，假设阻尼与质量、刚度之间的关系如下：

3 移动式反应堆的运输振动分析

3.1 移动式反应堆的参考模型

本节以前述6×12 轴轮式车辆为可移动式反应堆的运输车辆，分析移动式反应堆在不同等级道路运输下的振动响应特性。相关参数见表3［14］。

表3 车载设备质量及其质心坐标Table 3 Mass of vehicle equipment and its centroid coordinates

3.2 不同等级公路下的激励条件

国标GB/T 7031-2005［18］提出可将路面粗糙度分为A～H 共八个等级，A 级为最平滑的路面，H 级为最粗糙的路面。各级道路下的不平度范围如表4 所示。

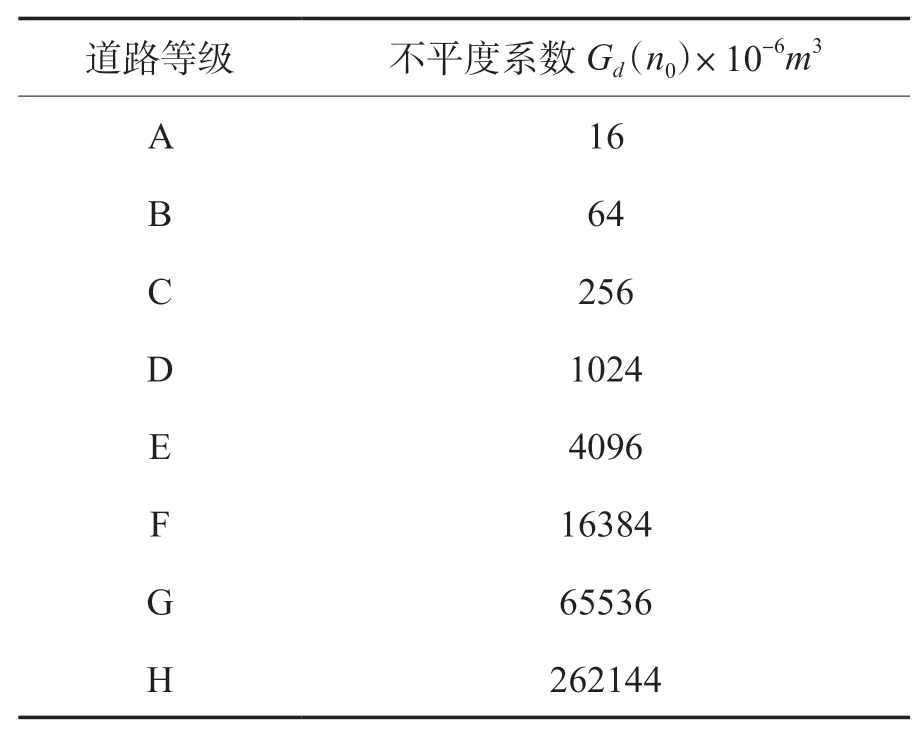
表4 不同等级道路下的不平度范围Table 4 Degree of roughness with different road classes

移动式反应堆在运输过程中，会遭受不同道路的激励。不同的公路等级下道路不平顺系数不同，从而对运输车辆产生的激励也会不同。一般采用空间频率Gd（n0）与道路位移功率谱密度函数Gd（n）之间的关系来描述车辆在随机激励下的振动情况：

式中，n为空间频率，n0为参考空间频率，ω为频率指数，Sv（ω）为轮胎底面位移激励功率谱密度。

本文采用谐波叠加法对车辆的左右轮时程激励进行模拟，得出左右轮的激励函数：

式中，θi，αi（i= 1，2，…，N）是在（0，2π）随机独立分布的数，bt是左右轮距，Sv（ω）是轮胎受路面激励的位移功率谱密度，γ（bt，ω）是左右轮胎受激励的谱相关函数。

3.3 分离式模型与集中式模型下的路谱激励对比验证

D 级公路是最常见的公路等级，在此等级公路下的计算结果具有普遍性。本节假设车辆行驶在D 级路面，行驶速度为20 km/h。利用Matlab 软件编写代码，对本文所建立的分离式模型下所受的路谱激励仿真，与文献［14］所建立的集中式质量模型进行对比，如图5 所示。

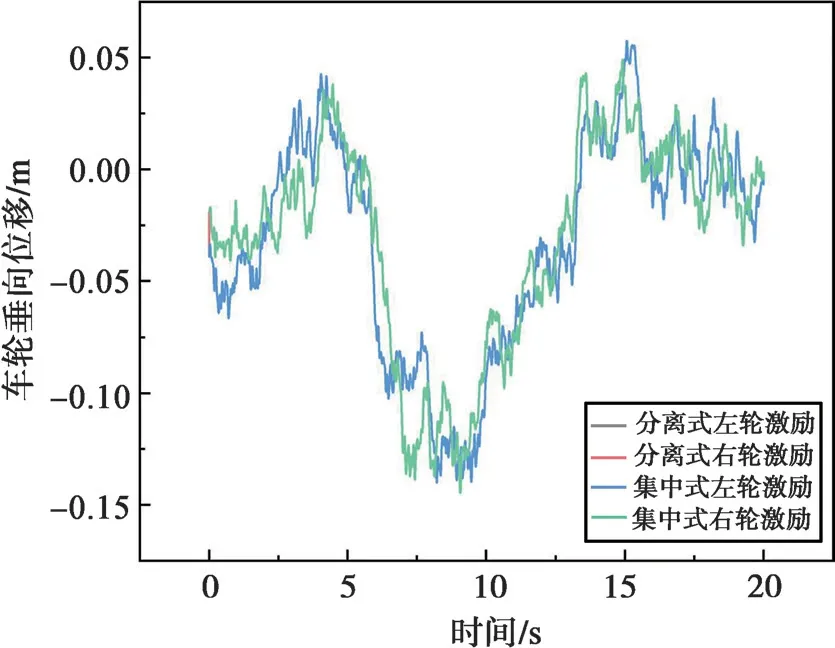
图5 分离式与集中式模型下的激励Fig.5 Loadings under the separated model and integrated model

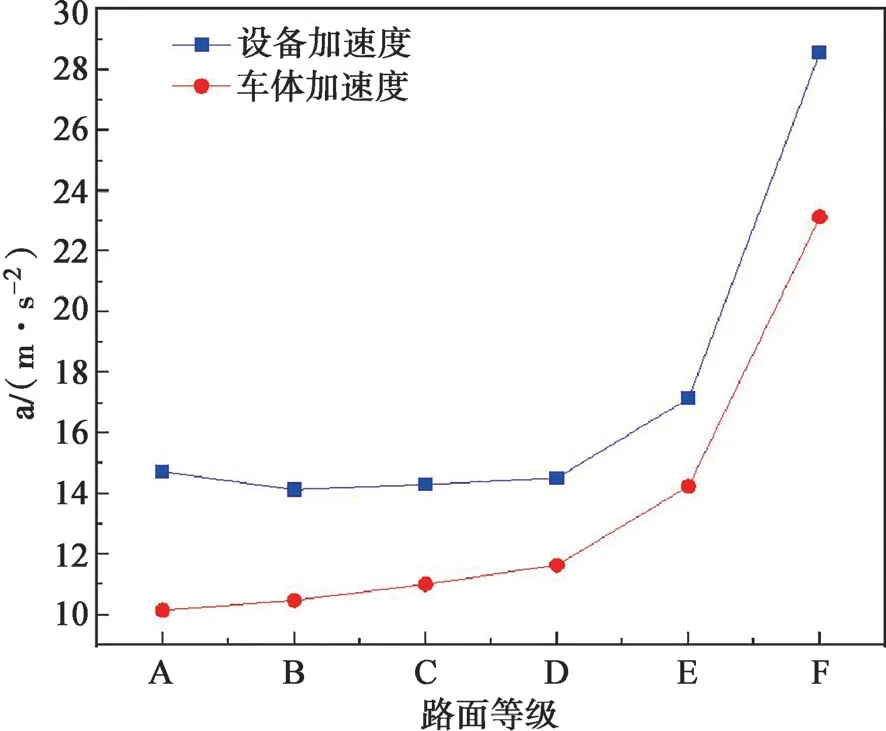
图6 冷却剂排空时不同公路等级下的加速度Fig.6 Accelerations of group 1 under different highway class

图7 冷却剂充满时不同公路等级下的加速度Fig.7 Accelerations of group 2 under different highway class

由图5 可以得出，分离式质量下的模型与集中式模型仿真得出在运输路面不平度激励下车辆车轮处的激励基本一致。由此可证明本文所建立分离式质量建模的方法的可行性。

3.4 车载运输的不同载荷条件

基于前文的研究，本节利用Matlab 仿真软件编写计算机程序，对六轴运载车辆的路面不平度激励下的振动响应进行仿真。假设车速20 km/h，分析车体和反应堆在D 级路面激励下的振动响应情况。

由于车载反应堆的冷却剂充排状态的不同使反应堆质量不同，车载反应堆与车体相连的三个方向（X/Y/Z）上的弹簧需依据不同的质量来选取不同长度，具体参数见表5。反应堆设备的质量根据不同冷却剂状态可分为：

表5 X/Y/Z 三个方向的弹簧刚度和长度取值Table 5 Values of spring stiffness and length in three directions of the reactor

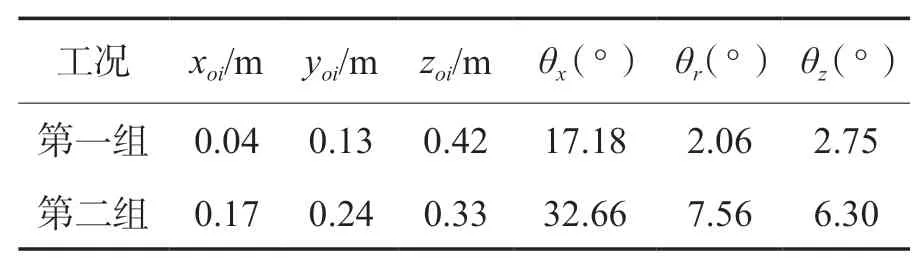
表6 反应堆设备六个方向的最大位移Table 6 Maximum displacement in six directions of the equipment

表7 车体三个方向的最大位移Table 7 Maximum displacement in three directions of the vehicle body

（1）第一组：当冷却剂LBE 排空下，此时反应堆设备质量为10 t，车体质量为20 t。

（2）第二组：当冷却剂LBE 充满下，此时反应堆设备质量为40 t，车体质量为20 t。

X/Y/Z 三个方向的刚度现取值为2.2×106N/m、2.2×106N/m、2.8×106N/m。X 方向代表水平横向，Y 方向代表水平纵向，Z 方向代表设备垂向。θx代表设备横向倾侧角位移，θy代表设备的纵向俯仰角位移，θz代表绕Z 轴转动的横摆角位移响应。φx代表车体的左右倾侧位移，φy代表车体的前后俯仰位移。

由以上分析可得，运输过程产生的位移与反应堆的质量成正比。在反应堆各个方向中，以垂向位移zoi和横向倾侧角位移θx的变化最大，在行驶过程中要多注意车辆的倾侧安全。当冷却剂充满时，反应堆容器的Z 方向振动幅度相似，其余各个方向的振动响应明显大于冷却剂排空工况。说明在反应堆运输过程中，应尽量保持冷却剂排空状态。

3.5 不同公路等级下整车系统的运输振动

运输车辆以20 km/h 速度行驶，分析在冷却剂不同充排量的情况下（分类如3.3 节），国内大部分公路是在A～F 等级道路，G、H 级公路粗糙度太大，本节选取路面等级A～F 分析整车振动响应。

由上述得知，反应堆与车体的振动比与二者的质量有显著相关性，在冷却剂排空时，反应堆与车体的质量比为1∶2，振动比值为2∶1，在冷却剂充满时反应堆容器与车体质量比为2∶1，振动比值为1∶2。二者的质量比与振动比成反比关系。在B、C、D、E 等级下车体和反应堆的加速度增长幅度不大，在F 级路发生陡升，因此应尽量避免移动式反应堆在F 级以上的道路上运输。

由图8 和图9 可以得出，不同等级道路下的加速度不同。当冷却剂排空时，振动峰值为3.84 Hz；当冷却剂充满时，振动峰值为3.22 Hz。在不同等级公路下的振动频率区间都集中在16 Hz 以内，超过此频率后振动趋于稳定。后续反应堆结构设计时应当避开此频率。

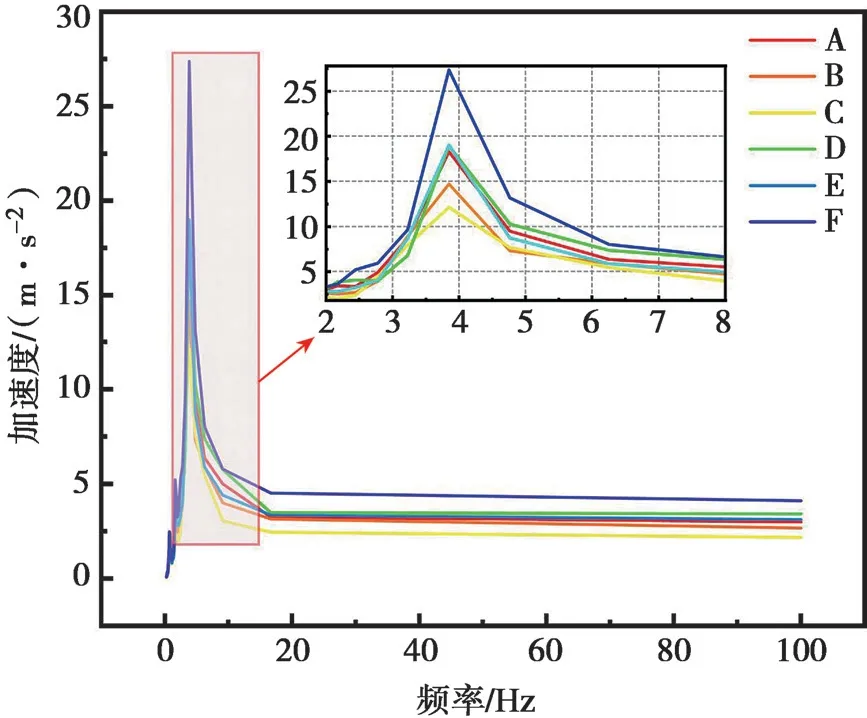
图8 反应堆设备10 t 车体20 t 等级A～F 公路下设备的加速度反应谱图Fig.8 Accelerations response spectrum of group1 under A～F class

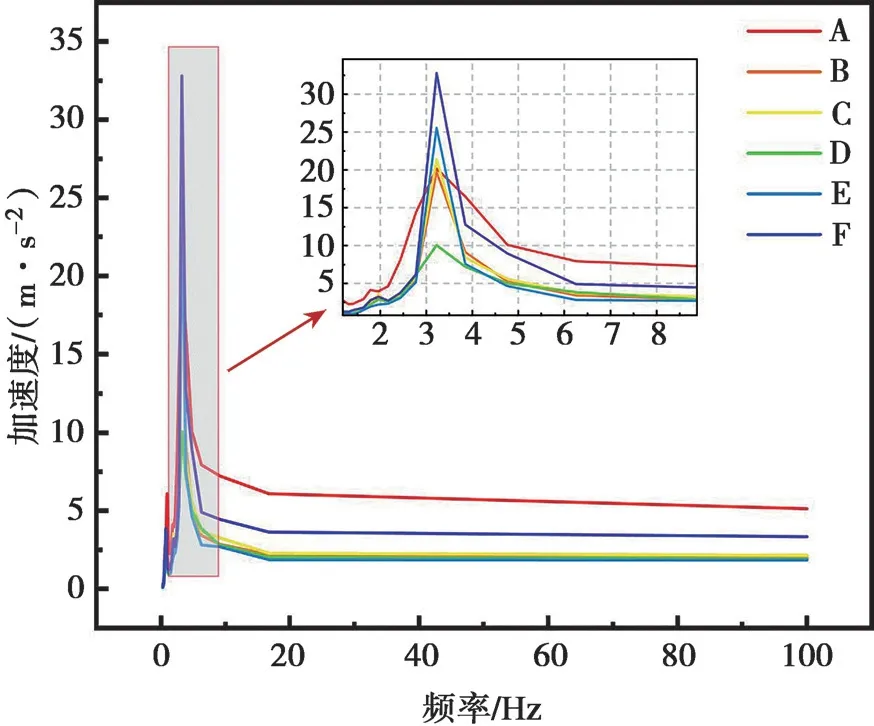
图9 反应堆设备40 t 车体20 t 等级A～F 公路下设备的加速度反应谱图Fig.9 Accelerations response spectrum of group 2 under A～F class

4 结论

本文围绕移动式反应堆的公路运输振动问题，建立了新型路面-车辆-设备多体动力学模型，并基于典型车载反应堆，开展了在不同公路等级条件和不同载重条件下的振动响应特性分析，为移动式反应堆的设计提供一定的参考。所得结论总结如下：

（1）本文建立了路面-车辆-分离式设备的多体动力学模型，相比于传统集中式质量模型，本文增加了6 个自由度，该6 个自由度为描述反应堆设备处的横向位移xoi、纵向位移yoi、垂向位移zoi、倾侧角位移θx、俯仰角位移θy、横摆角位移θz。通过此模型，能够更好地刻画移动反应堆多个设备分散布置的特征，且计算量没有显著增加。

（2）在D 级公路条件下，考虑冷却剂排空与充满两种工况条件，当冷却剂充满时，反应堆容器的Z 方向振动幅度相似，其余各个方向的振动响应明显大于冷却剂排空工况。因此在反应堆运输过程中，应尽量保持冷却剂排空状态。

（3）在D 级公路下，反应堆与车体的振动比与二者的质量有显著相关性，在冷却剂排空时，反应堆与车体的质量比为1∶2，振动比值为2∶1，在冷却剂充满时反应堆容器与车体质量比为2∶1，振动比值为1∶2。二者的质量比与振动比成反比关系。

（4）在不同公路等级下，系统的振动主频相似，集中在16 Hz 以内。振幅随着公路等级的恶化逐步增大，在F 级公路后发生陡升。增幅达到150%，运输过程存在安全隐患，应尽量避免可移动式反应堆在F 级以上更粗糙的道路运输。

本文能够为移动式反应堆在不同公路等级下的运输提供工程借鉴和安全性指导。

致谢：感谢凤麟核团队的支持，以及国家重点研发计划No.2020YFB1902102、No.2020YFB1901901的资助支持。