基于SSA-BP神经网络的圆钢管RPC短柱轴压承载力预测

卜良桃,洪俊鹏

(湖南大学土木工程学院,湖南 长沙 410082)

随着我国经济不断发展,大跨度结构、高层建筑不断涌现,对轴心受压构件的承载力有了更高的要求,型钢-混凝土组合结构应运而生。圆钢管活性粉末混凝土柱作为其中的代表,通过将活性粉末混凝土(Reactive Powder Concrete,RPC)填充于圆钢管中,借助圆形钢管对核心混凝土的套箍约束作用,使核心区RPC处于三向受压状态,使RPC的塑性和韧性有效改善,承载力和变形性能大幅提升[1]。承载力计算是结构设计的基础,由于RPC具有高强的特点,当前规范[2-4]对材料强度又有所限制导致适用性较差,因此众多学者针对各影响因素与承载力之间的关系开展研究。王彦博[5]考虑提高混凝土强度对约束效应的减弱,对规范[3]的计算公式进行系数修正,使钢管高强、超高强混凝土柱的安全保证率得以提高。J.P.Liu等[6]提出钢管应力的表达式,以此为基础建立承载力预测公式,预测结果与试验值平均比值为0.912。但以上研究预测精度偏低,这是由于各影响因素相互耦合,与承载力间呈现出非线性映射关系,从而导致传统方法难以实现圆钢管RPC柱轴压承载力的高精度预测。

目前机器学习算法发展迅速,其中BP神经网络由于其出众的非线性拟合效果,在承载力预测上得到广泛使用。V.L.Tran 等[7]基于BP神经网络对圆钢管RPC柱承载力进行预测,预测精度相比于规范[2-4]得到提升。陆征然等[8]使用双隐含层BP神经网络实现了对缺陷圆钢管混凝土短柱承载力的预测。M.Ahmadi等[9]采用BP神经网络对钢管混凝土柱承载力预测,平均误差为11.17%,低于其他数学模型。但也有学者指出,由于算法的局限性,BP神经网络对预测精度的提升有限,稳定性也不足[10]。因此,笔者拟对BP神经网络承载力预测模型进行进一步优化。麻雀搜索算法(Sparrow Search Algorithm,SSA)作为一种新型智群搜索算法,于2020年[11]提出,在单峰函数和多峰函数全局寻优测试中表现出良好的收敛精度、稳定性和收敛速度。在土体开挖受损区域厚度的预测研究中,BP神经网络经过SSA算法优化后均方根误差降低43.06%[12]。此外,在降雨预测[13]等研究中,SSA算法也表现出对BP神经网络的良好优化能力,但目前SSA-BP神经网络在承载力预测问题上的使用却并不广泛。

为建立高精度圆钢管RPC短柱轴压承载力预测模型,笔者引入SSA算法对BP神经网络的初始权重、阈值进行优化,形成SSA-BP神经网络预测模型,并与其他预测模型进行综合对比分析。研究表明:使用SSA-BP神经网络对圆钢管RPC短柱承载力进行预测具备可行性,在预测精度、预测效率、模型稳定性等方面表现良好。

1 数据库建立

1.1 数据来源

建立BP神经网络预测模型,首要问题是获取足量的样本数据。笔者统计文献[14-22]中共计155组圆钢管RPC短柱轴压试验数据,如表1所示。

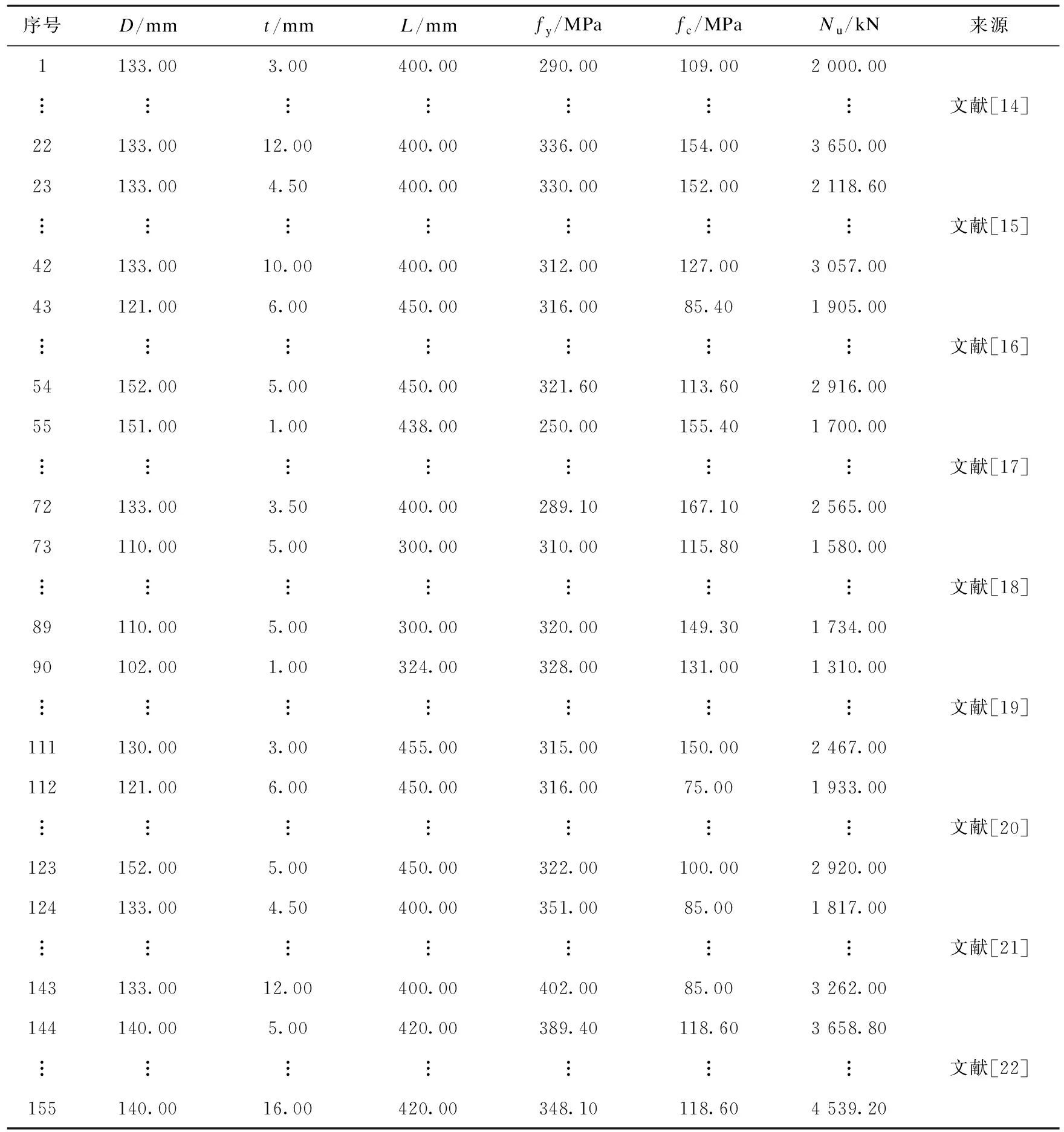
表1 圆钢管RPC短柱轴压试验数据Table 1 The axial compression experimental data of RPC filled circular steel tube stub columns

1.2 数据分析

数据库中,试验变量为柱外直径D、钢管壁厚t、柱高度L、钢管屈服强度fy和RPC抗压强度fc,分析试验数据的构件几何参数和材料强度参数见表2,其中标准差和变异系数用于评估各参数的离散程度。

数据库各参数的频率分布如图1所示。由图可知,各变量分布相对集中,D与L分别集中分布在130～140 mm和380～460 mm,这是由于试验中常把柱高设置为柱外径的3倍,而外径133 mm的钢管可直接购置成品钢管,对应型号为DN125,且此时构件大小适宜试验,因此较多学者选择直径为133 mm、高为400 mm的试验构件;数据库中钢管壁厚、钢管屈服强度和RPC抗压强度主要分布于常见范围。

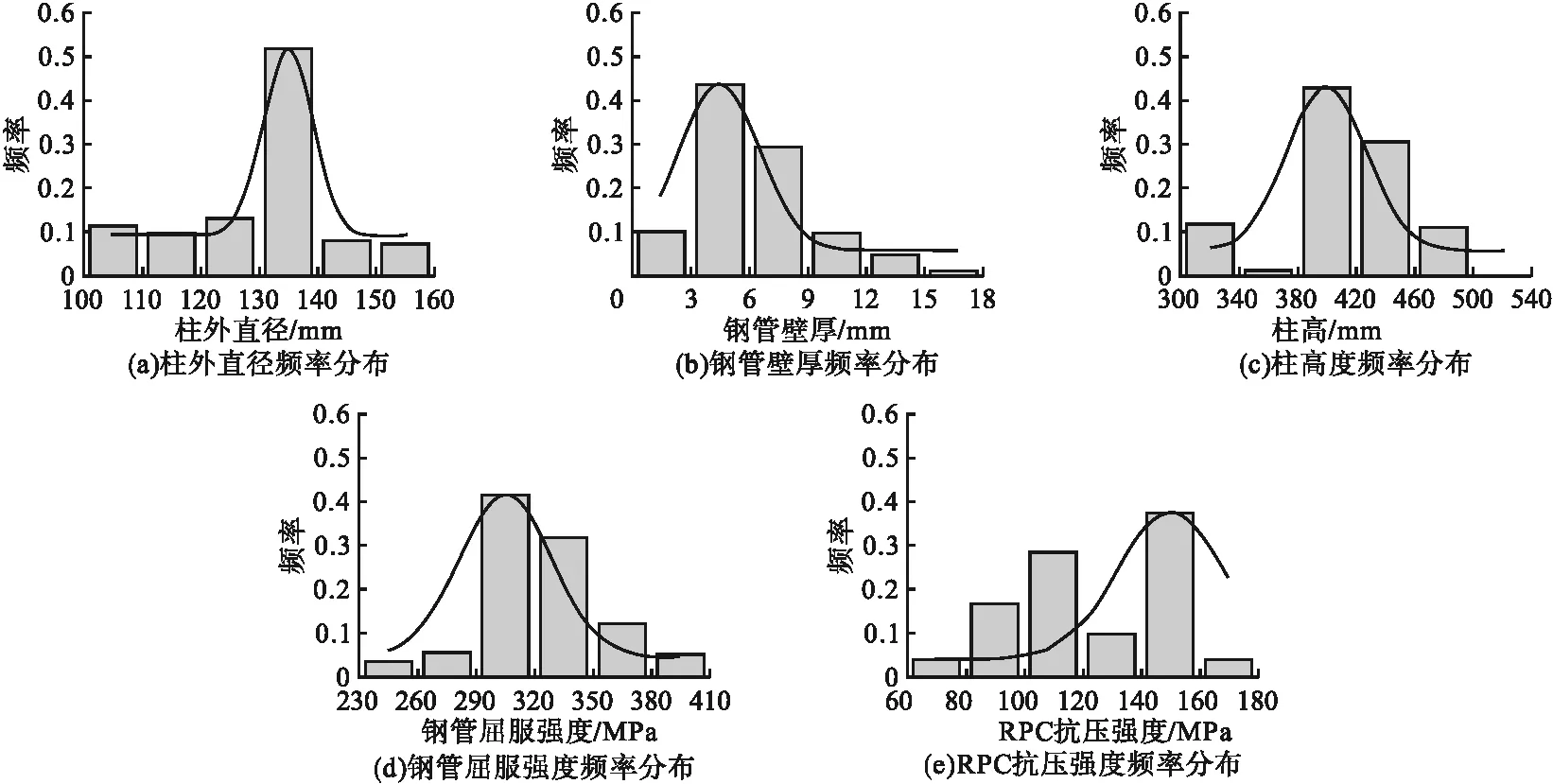
图1 数据集各参数频率分布Fig.1 Frequency distribution of parameters in the data set

2 SSA-BP算法原理及流程

2.1 SSA算法原理

SSA算法是通过模拟麻雀种群的捕食行为而提出的一种新型智群算法,其生物原理为:根据麻雀种群在捕食过程中的行为,将其划分为发现者、加入者两种角色。发现者在发现食物后释放信号给加入者,共同获取食物,在捕食过程中,麻雀会在发现者和加入者两种角色中转换。种群中的个体也会综合自身危险程度和体能,判断自身是否为危险者,危险者会更注意周围天敌的活动情况,在发现危险时,释放信号使种群转移至安全区域。基于此原理,麻雀种群得以实现高效率获取食物,并躲避天敌的攻击。具体数学建模过程可参考文献[11]。

2.2 SSA-BP神经网络实施流程

传统BP神经网络通过对数据间隐含关系的挖掘,进行数据拟合,从而实现数据预测。由于结构简单、非线性拟合能力强等特点,在承载力预测方面得到广泛运用。但在实践过程中,也显现出一些不足,由于训练的局限性,存在误差偏高、初始权重和阈值具有随机性、稳定性差、容易陷入局部最优化等不足。

针对BP神经网络的不足,本研究使用SSA算法对BP神经网络进行优化,同时以一种更利于寻优的方式对BP神经网络的隐含层节点数进行优选,具体算法流程如图2所示。

图2 SSA-BP神经网络流程图Fig.2 The flow chart of SSA-BP neural network

(1)数据输入与归一化处理。将试验数据库随机划分为训练样本集(75%)和测试样本集(25%)。其中,116组作为训练样本,用以训练模型达到最佳预测状态;39组为测试样本集,用以验证各模型的预测效果。由于所收集的数据集各变量数量级相差较大,需要将其映射在小范围内,采用式(1)进行归一化处理:

(1)

式中:xi为归一化之后的数据;x为原始数据;xmax、xmin分别为原始数据组中的最大值和最小值;ymax、ymin分别为共同决定归一化后值域的最大值和最小值。本研究中选择将各影响因素归一化至[0,1]内,轴压承载力归一化至[-1,1]内。

(2)算法参数设置。在BP神经网络部分,选择“Tansig”函数作为神经网络输入层至隐含层之间的激励函数,“Purelin”函数作为隐含层至输出层之间的激励函数,训练方法选择L-M算法,训练次数设置为100,学习率设置为0.01,训练目标误差为10-6。GA算法与SSA算法部分,保持相似的设置状态,种群数量设置为20,最大迭代次数为15。

(3)确定隐含层节点数范围。本研究中输入层节点选择D、t、L、fy和fc,输出层节点选择Nu,输入层、输出层节点数分别为5和1。根据式(2)确定隐含层节点数范围,确定拓扑结构为5-Ihid-1,其中Ihid∈[3,12],单次程序运行只需训练模型10个。

(2)

式中:Ihid为隐含层节点数;Iin为输入层节点数;Iout为输出层节点数。

(4)SSA算法优化BP神经网络初始权重和阈值。基于SSA算法,以预测值与实际值之差作为种群适应度,寻找适应度最小的位置作为最优解。每次迭代更新种群中麻雀定位,即重新确定发现者、加入者,同时确定10%～20%的个体为警戒者。重复迭代寻优,直至达到最大迭代次数。

(5)BP神经网络训练。将SSA优化所得初始权重、阈值赋予BP神经网络后,对权重与阈值进行迭代,直至神经网络达到最优预测状态,将模型存储于Matlab程序的单元数组cell中。将预设的拓扑结构依次进行训练并进行存储。

(6)神经网络仿真预测。以均方误差MSE为评价依据,对存储于cell中的各模型进行对比,调用最优模型进行圆钢管RPC短柱轴压承载力仿真预测。

以SSA-BP神经网络为例,各拓扑结构下神经网络的MSE如图3所示。当隐含层节点数为9时MSE最小,此时预测效果将达到最优,因此选择调用拓扑结构为5-9-1的模型进行仿真预测。

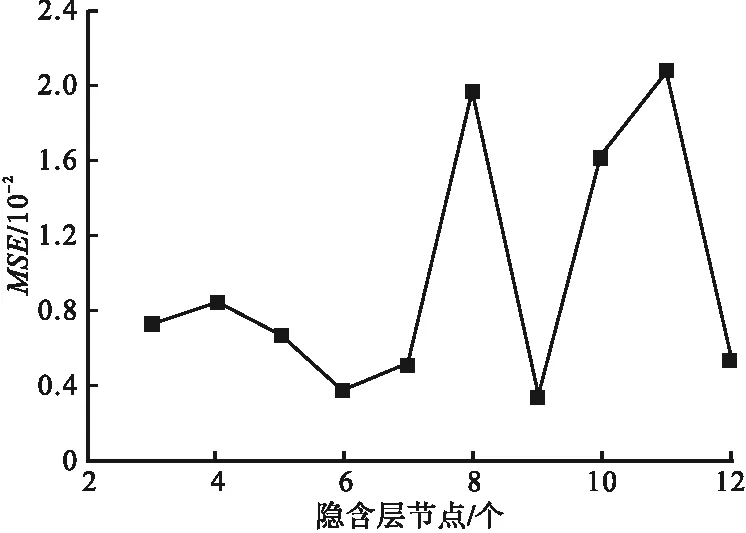
图3 不同隐含层节点数下的MSEFig.3 The MSE of different nodes in hidden layer

3 预测结果与分析

3.1 模型评价标准

为验证SSA算法对BP神经网络的优化效果及优化模型适用性,试验分为三部分:建立BP神经网络模型、GA算法优化BP神经网络模型和SSA算法优化BP神经网络模型,分析SSA算法对BP神经网络的优化效果,对比SSA-BP神经网络与计算公式的预测能力。

引入均方误差MSE、均方根误差RMSE、决定系数R2用以评价预测精度及模型稳定性。计算公式如下:

(3)

(4)

(5)

3.2 神经网络模型预测结果对比

训练BP神经网络、GA-BP神经网络、SSA-BP神经网络至稳定状态,对测试样本进行预测,评价参数如表3所示。GA-BP 神经网络和SSA-BP神经网络的MSE值相比于BP神经网络分别降低67.45%和79.05%。可以看出,GA算法与SSA算法都能有效提高BP神经网络对圆钢管RPC短柱轴压承载力的预测精度。SSA-BP神经网络的R2值为0.974 9,相较于另外两种模型更接近于1,说明在相同的数据集上,SSA-BP神经网络具有更高的预测精度。

表3 承载力预测评价参数Table 3 Evaluation parameters of bearing capacity prediction

将BP神经网络、GA-BP神经网络、SSA-BP神经网络的预测值、预测误差统计,结果如图4、图5所示。由图可知,BP神经网络在承载力的预测上存在较大误差,误差平均值为193.20 kN,最大相对误差为74.41%;GA-BP神经网络相较于BP神经网络的预测效果有一定程度的提升,其误差平均值为121.41 kN,最大相对误差为29.43%;SSA-BP神经网络在预测效果上有了进一步的提升,其误差平均值为106.34 kN,最大相对误差为17.30%。

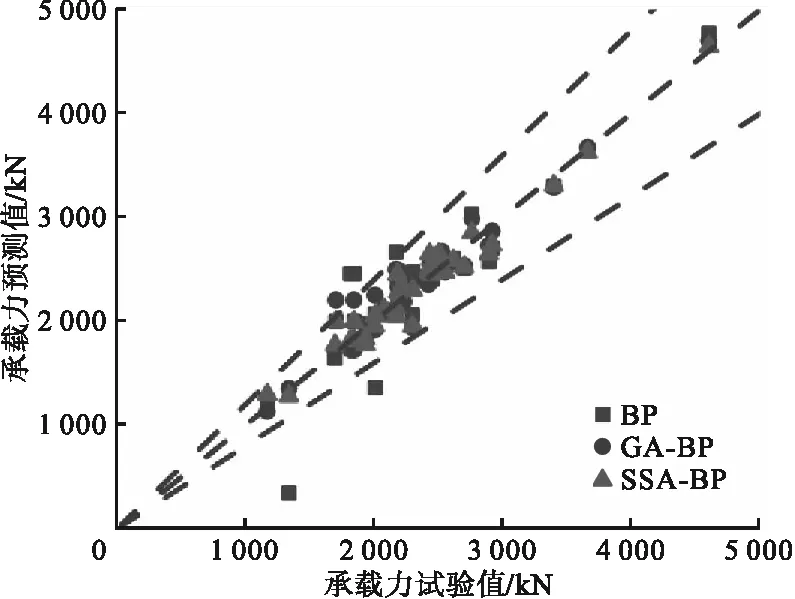
图4 承载力预测值与试验值比较Fig.4 The comparison between predicted value and experimental value of bearing capacity

图5 预测误差分布Fig.5 The distribution of predicted error

为比较GA-BP神经网络和SSA-BP神经网络的稳定性,对两种模型各进行100次模拟训练,以R2作为评价依据,统计R2值累计频率分布情况,如图6、图7所示。由图可知,SSA-BP神经网络的R2值大于0.950的频率为0.56,比GA-BP神经网络高出0.18。同时,GA-BP神经网络的R2值在各区间内分布均匀,而SSA-BP神经网络集中于0.965附近,相较而言SSA-BP神经网络更为稳定。另一方面,SSA-BP神经网络和GA-BP神经网络单次训练时间分别为182 s和327 s,使用SSA算法进行模型优化相比于GA算法使程序运行时间降低44.34%,对于需要重复训练调试的程序而言,这种效率上的提升有重要意义。综上所述,相比于GA算法,使用SSA算法进行BP神经网络优化,效果更为稳定,程序调试时间明显缩短。

图6 GA-BP神经网络R2值累计频率分布Fig.6 The cumulative frequency distribution of R2 in GA-BP neural network

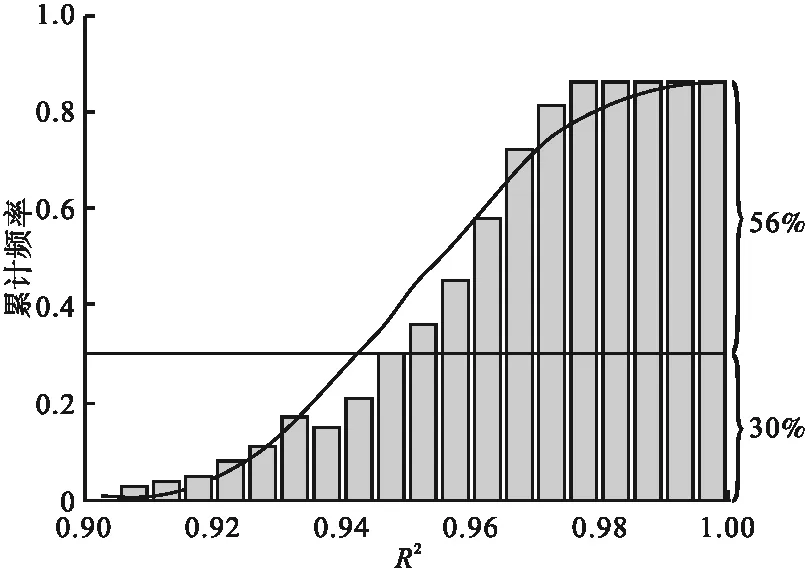
图7 SSA-BP神经网络R2值累计频率分布Fig.7 The cumulative frequency distribution of R2in SSA-BP neural network

3.3 SSA-BP模型与计算公式预测结果对比

目前学者们对于圆钢管RPC短柱承载力开展了一系列研究,笔者选择近年代表性成果与上文建立的SSA-BP神经网络进行对比。王彦博等[5]考虑了混凝土强度提高对约束效应的弱化,以大量试验数据为基础对欧洲规范进行修正,得到式(6)。J.P.Liu等[6]考虑到钢管与RPC之间存在黏结与摩擦,会对承载力产生影响,结合有限元模型,提出钢管应力简化表达式,推导得出式(7)。

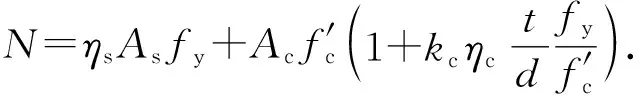
(6)

(7)

使用SSA-BP神经网络预测模型和式(6)、式(7)对数据库全体样本进行承载力预测,预测值和预测误差分布统计如图8所示。使用线性模型对预测值与实际值进行拟合,拟合所得直线斜率越接近1,则说明预测效果越好,在SSA-BP神经网络、式(6)和式(7)中拟合所得的直线斜率分别为0.973、0.580和0.672。从图8(a)～图8(c)也可以看到,SSA-BP神经网络的预测结果近乎分布在理想拟合线上,而式(6)、式(7)均有大量数据点位置距离理想拟合线较远。如图8(d)～图8(f),在相对误差率的分布上,SSA-BP神经网络误差分布更集中,波动幅度小,式(6)、式(7)预测结果误差波动较大。说明SSA-BP神经网络在预测精度上具有优势显著。

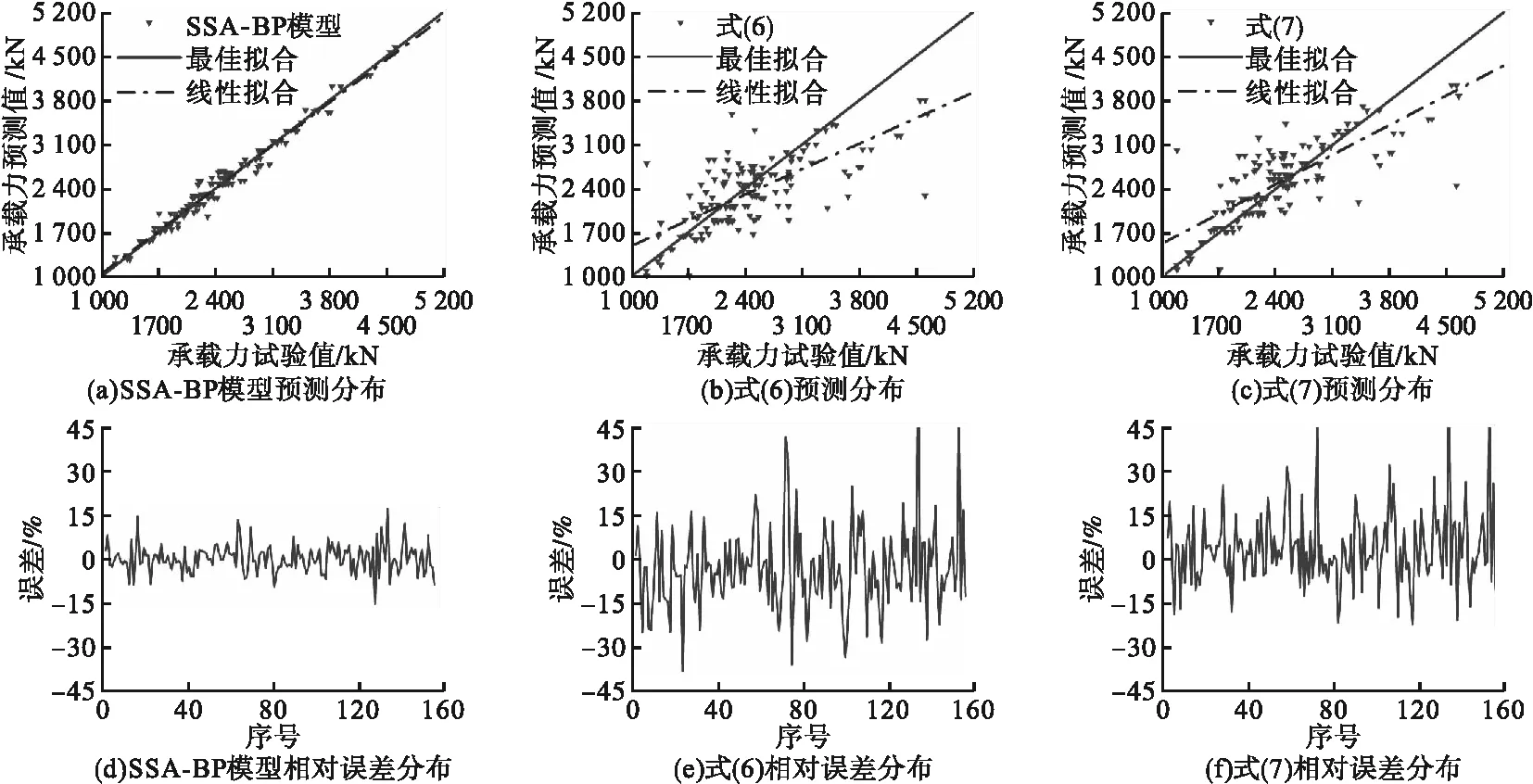
图8 承载力预测值、预测误差分布Fig.8 The distribution of bearing capacity prediction value and error SSA-BP

4 结 论

(1)针对传统BP神经网络在圆钢管RPC短柱轴压承载力预测问题上存在的稳定性差 、精度低等缺陷,引入SSA算法和GA算法,使预测精度分别提高了67.45%和79.05%,有效提高了BP神经网络的预测性能。

(2)在圆钢管RPC短柱轴压承载力预测问题上,SSA-BP神经网络相比于BP神经网络和GA-BP神经网络,具有最低的误差平均值、MSE值、RMSE值和最高的R2值。同时,SSA-BP神经网络单次训练时间较GA-BP神经网络缩短44.34%;在100次重复训练中,R2值分布也更加集中。说明SSA-BP神经网络能够实现圆钢管RPC短柱轴压承载力的高精度预测。

(3)将SSA-BP神经网络与式(6)、式(7)的预测结果进行对比,结果显示SSA-BP神经网络预测平均相对误差为3.66%,远高于公式预测精度,且误差分布更集中,波动幅度更小。说明SSA-BP神经网络适用范围更广,在设计过程中作为验算补充能提高结构的安全性。