基于树模型的糖尿病分类预测研究

汪艺璇

(河北地质大学经济学院,石家庄 050030)

0 引言

糖尿病是一种慢性疾病,目前还无法彻底治愈,其以高血糖为主要发病特征,会引发一系列的并发症。由于知晓率较低,往往患者发现患病时已经产生了一系列的并发症。若能找出糖尿病患者的相关特征,对其进行早期预测,防患于未然,可令患者更早的接受治疗,有助于更好地预防。目前,关于糖尿病分类预测的研究取得了一定的进展,汪迎归[1]提出优化及改进的Stacking分类预测模型,取得了较好的预测结果。杨雨含等[2]基于随机森林及序联合搜索的Wrapper式特征选择算法精度达到81.13%。刘文博等[3]基于迭代随机森林对糖尿病数据集进行分类,得到的分类结果较好。苗丰顺[4]使用了一种新型的Boosting算法进行糖尿病分类,预测效果较好。但目前基于树模型预测方法的糖尿病分类研究文献较少,树模型是以决策为基础的分类方法,包含单一的决策树及决策树组合模型。本研究以糖尿病分类为研究对象,分析对比了一系列树模型,如C4.5决策树生成算法、CART决策树生成算法、Bagging算法、随机森林、Adaboost算法等在糖尿病分类预测中的性能。

1 算法概述

树模型是一种以决策树模型为基础的模型,包括单一的决策树模型及组合的决策树模型。其中单一的决策树模型又发展出了不同的决策树生成算法,如C4.5与CART算法可用来生产决策树,这两种算法的区别在于特征选择方式不同,C4.5算法使用了信息增益比,CART算法则采用了基尼指数对特征进行分类。组合决策树模型是以单一的决策树模型组合生成一系列的树集体进行决策,如Bagging算法。主要思想是随机采样,即在训练集上随机采样,建立不同的决策树,合成一个强分类器,合成的方法为简单投票法,得到票数最多的标签类别作为投票结果。随机森林算法也称为Bagging的加强版,对决策树的建立做了一些改进,在建立过程中引入随机特征选择。Adaboost算法是用加权多数表决的一种决策树集成方法,在训练过程中如果某个样本在前一轮决策树的建立中被错分,那么在建立下一棵决策树时就会给它较大的权重,令其受到更多的关注。

1.1 决策树

决策树模型整体结构像一棵树,从最开始的一个节点出发,通过数据训练选择最优特征并不断分叉下去,是很好的一种分类方法,当决策数据结果训练好以后,输入样本便能预测出该样本属于哪种类别,适用于糖尿病分类问题。本研究主要探究决策树生成算法中的C4.5与CART算法。

在C4.5生成算法[5]中,以信息增益比进行特征选取,若设训练集为D,特征为A,信息增益为g(D,A),训练集D关于特征A的值的熵为HA(D),具体表达式如下:

(1)

其中,n为特征A取值的个数,特征A对训练集D的信息增益比为其信息增益与HA(D)的比,具体表达式为:

(2)

在CART生成算法[6]中,以基尼指数进行特征选择,假设有K个类,样本点属于第k类的概率为pk,那么概率分布的基尼指数定义表达式为:

(3)

由于糖尿病分类是一个二分类问题,若设样本属于糖尿病的概率为p,则概率分布的基尼指数表达式具体为:

Gini(p)=2p(1-p)

(4)

对于一个给定的样本集合D,基尼指数按照如下公式定义:

(5)

其中,K是类总共的数目,Ck是D中属于第k类的样本的一个子集。

1.2 决策树组合模型

决策树组合模型则是把许多的树组合在一块进行分类预测,单棵树的学习能力一般不如许多个树一块学习,这样集成起来的分类预测能力强。若把单棵树看做弱分类器,那么决策树组合模型就是合成多个树,每个树的结果综合在一块,然后一起给出最终结果,根据特征选择方式及弱分类器集成方式的不同形成了多种决策树组合模型,包括Bagging算法、随机森林算法、Adaboost算法。

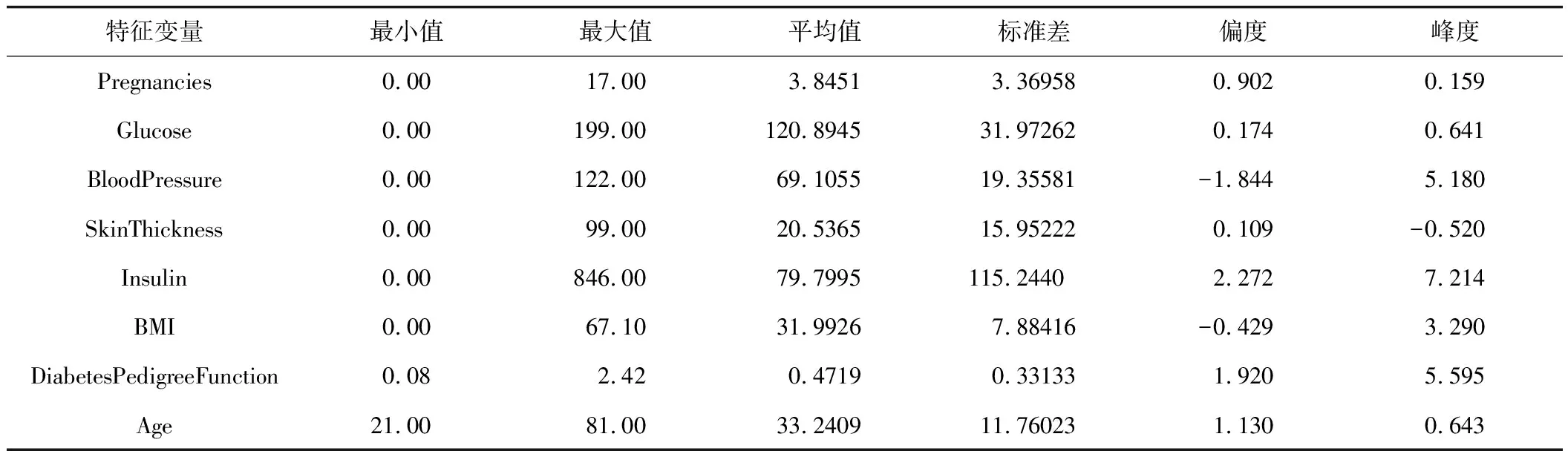
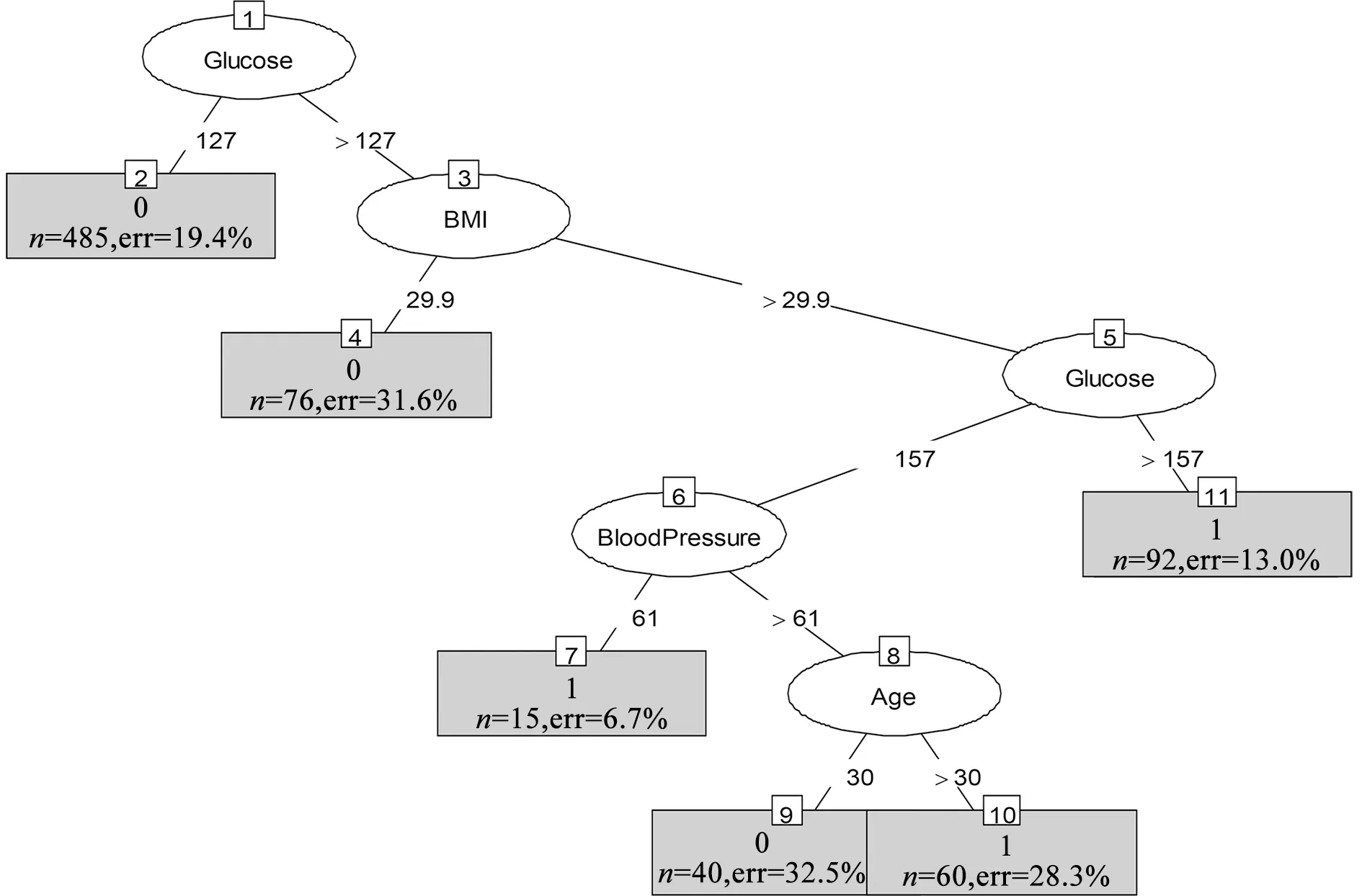
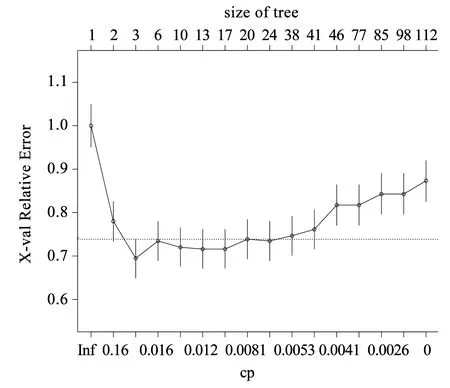
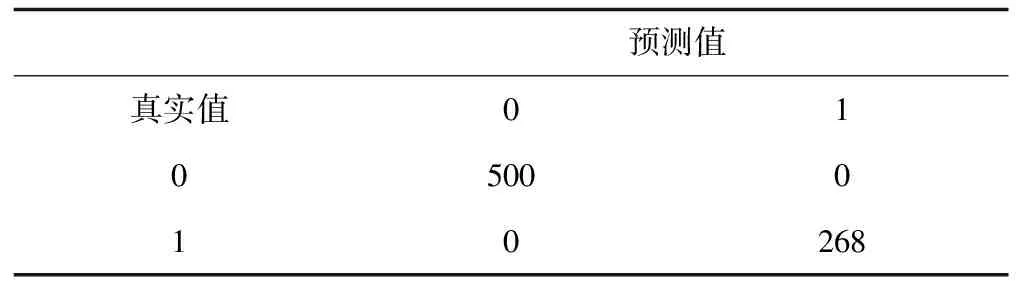
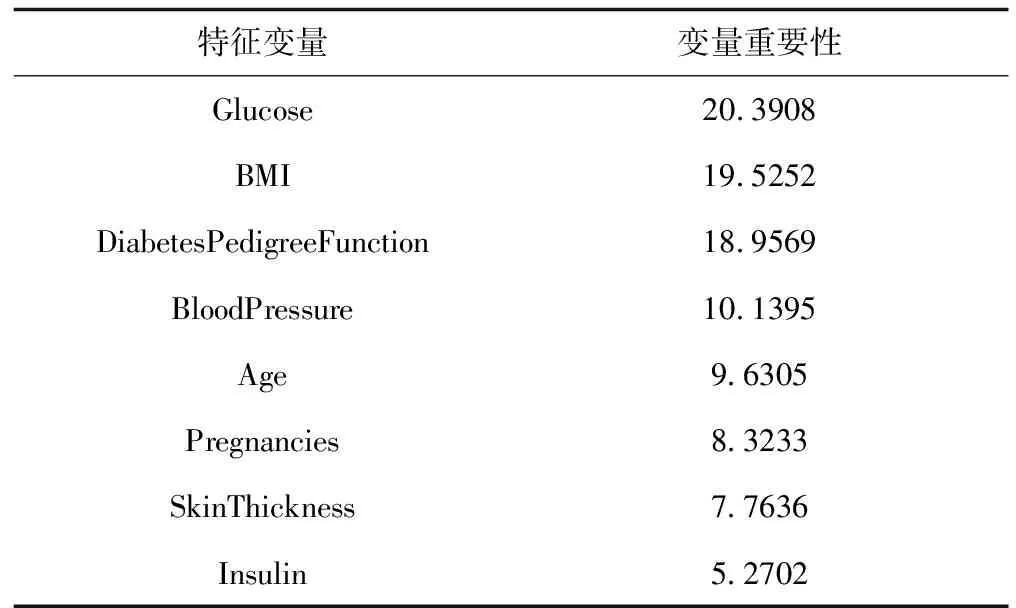
Bagging算法是一种相对于随机森林与AdaBoost算法简单得多的算法。这种算法的思想很简单,是把每个决策树看做是一个人,很多人组成一个群体,那么要决策一件事情时,每个人都形成一种自己的判断,然后所有人一块进行投票,得到最多的类别作为最终的决策。以糖尿病分类预测为例,在Bagging算法中,设样本集为D={(x1,y1),(x2,y2),…,(xm,ym)},其中m代表样本量,为768,xi(i=1,2,…,m)∈R8,yi(i=1,2,…,m)∈R,t=1,2,…,T,每次采样m′(

(6)

随机森林算法[7]是一种使用广泛的集成树分类算法,因其良好的分类性能得到了人们的认可,是Bagging算法的升级版,对t=1,2,…,T每次在集合D中随机采样形成集合Dm′,但是整个过程与Bagging算法不同,在训练决策树模型节点时,只选取一部分样本特征,在其中选择一个最优特征来做决策树的下一步分叉决策,形成弱分类器Mt(Dm′),最终综合成强分类器,其表达式为:

(7)

Adaboost算法[8]的总体思想是形成一系列弱分类器,再组合成强分类器,但与前两种组合算法存在极大的不同。如弱分类器组成强分类器的方法不同,不再采用简单随机投票得票多胜出的方法,而是进行一定的综合,这种综合体现为偏重多数的决策办法,即在决策时向分类误差率小的树进行偏斜。在构建下一轮弱分类器时,更加重视被前一轮树分错的样本,算法步骤是对数据的权值分布进行初始化,即:

(8)

对t=1,2,…,T用具有Wt的训练集进行学习得到分类树Ηt,计算它的分类误差率:

(9)

计算它的系数为:

(10)

更新训练集的权值分布为:

(11)

构建多个树的线性组合,得到最终的模型为:

(12)

2 模型构建与结果

2.1 数据来源与预处理

数据来源为UCI上的糖尿病数据集,该数据集共有样本768条,数据中给出了每个样本的分类标签,其中为糖尿患者的样本为268,非糖尿病患者的数据500条,可见样本标签分类较为均衡,比值约为3∶5。数据集的特征变量共有8个,变量名称分别为Pregnancies、Glucose、BloodPressure、SkinThickness、Insulin、BMI、DiabetesPedigreeFunction、Age,取值均为连续型数据。利用这8个特征数据训练分类器之前,检查原始数据集,观察其中是否有缺失,发现数据集较完整,无缺失,较为理想,将数据格式调整为数值型数据即可投入分类器训练中。

2.2 数据的描述性统计

对数据的描述性统计分析可以从总体上掌握统计特征,故对糖尿病患者的8个特征变量数据进行描述性统计,包括数据最大值、最小值等,结果如表1所示。

表1 特征变量的描述性统计分析

通过对8个特征变量的描述性统计分析可知,Pregnancies的最小值为0,最大值为17,平均值为3.8451,标准差为3.36958,偏度为0.902,峰度为0.159,Age的最小值为21岁,最大值为81岁,平均为33岁,以此类推,可以得到其他各特征变量的描述性统计结果。2.3 两种决策树模型的建立与结果分析

C4.5算法下的模型,利用R软件进行决策树的建立及结果分析,利用数据训练出决策树,绘制出原始的决策树,发现其枝叶较为繁茂,故需要对决策树进行修剪,主要通过参数U进行设置,参数U代表不对决策树进行剪枝,默认值为True,将模型的参数U设置为False,并将剪枝过程的置信阈值设为0.05,每个叶结点最小观察样本量设置为6。参数B代表每个节点仅分为两个分支,默认值为True,设置为False。绘制简化版的决策树如图1所示。

图1 决策树C4.5

建立CART算法生成的决策树模型,利用数据训练出原始的决策树,发现训练出的模型较为复杂,故综合模型复杂度及预测精度进行了决策树剪枝,计算复杂度列表并进行可视化,绘制了模型复杂度与模型错误率的关系图,如图2所示。

图2 复杂度与模型错误率关系图

经过综合考量,选取复杂度为0.01,建立决策树如图3所示。

图3 决策树CART

给出以上两种算法下决策树的分类混淆矩阵及模型预测精度。经过分析,训练并建立最终的决策树模型,为了比较分析两种模型的预测性能,给出分类预测混淆矩阵如表2、表3所示。

表2 决策树C4.5分类预测混淆矩阵

表3 决策树CART分类预测混淆矩阵

由表2、表3可见,决策树C4.5将30名未患糖尿病的人错分成了糖尿病患者,还有131名糖尿病患者没有识别出来,而决策树CART将44名未患糖尿病的人分成了糖尿病患者,还有88名糖尿病患者没有识别出来。根据这两个混淆矩阵,计算了C4.5算法与CART算法生成的决策树预测错误率分别为20.96%、17.19%,可见CART算法生成的决策树对糖尿病的分类预测效果更好一些。

2.3 三种决策树组合模型的建立与结果分析

Bagging算法较为简单,主要通过建立多个决策树进行投票,观察哪个得票最多,从而做出决策。在随机森林算法中,可根据OBB错判率来决定树的棵数,故绘制随机森林的OBB错判率及决策树棵树之间的关系图进行判断。利用R软件绘制的OBB错判率及决策树棵树之间的关系如图4所示:

图4 OBB错判率与决策树棵树之间的关系

通过图4可以看出,当建立的决策树棵树为100棵时,随机森林的模型错判率趋于稳定,故采用100棵树建立随机森林模型。Adaboost算法是通过多棵树建立决策树组合预测,不再采取简单投票而是进行线性综合,利用R软件依据糖尿病数据进行模型拟合。

对建立的3种决策树组合模型在糖尿病数据集上的分类性能进行分析比较,给出3种决策树组合模型分类预测的混淆矩阵,如表4、表5、表6所示。

表4 Bgging算法分类预测混淆矩阵

表5 随机森林算法分类预测混淆矩阵

表6 Adaboost算法分类预测混淆矩阵

由表4、表5、表6可见,Bagging算法只将1名未患糖尿病的人错分成了糖尿病患者,只有8名糖尿病患者没有识别出来。随机森林算法与Adaboost算法则全部分类正确,所有糖尿病患者都识别出来了,且没有把未患糖尿病的人错分为糖尿病患者。根据这3个混淆矩阵计算Bagging算法、随机森林算法及Adaboost算法在糖尿病分类预测中的错误率分别为1.17%、0%、0%,可见随机森林算法与Adaboost算法生成的决策树对糖尿病的分类预测效果更好一些。

2.4 糖尿病分类预测变量的重要性分析

通过以上2种决策树生成算法及3种决策树组合预测模型的分类结果可知,这5种树模型的分类预测性能从总体上看,3种决策树组合分类模型皆优于单一的决策树分类预测模型,证实了决策树组合模型在糖尿病分类预测中的优越性。选择Adaboost模型作为糖尿病预测模型,进行输入变量的重要性分析,以确定影响糖尿病发生的重要特征,为糖尿病的预防提供参考。利用R软件计算出8个糖尿病特征变量的重要性,如表7所示。

表7 特征变量重要性

为了更直观地看出8个变量的重要性大小关系,进一步对8个变量的数据重要性进行可视化,绘制成柱形图如图5所示。

图5 输入变量的重要性

由图5可知,对糖尿病患者进行分类预测的过程中,变量重要性从大到小依次为Glucose、BMI、DiabetesPedigreeFunction、BloodPressure、Age、Pregnancies、SkinThickness、Insulin。其中,Glucose、BMI、DiabetesPedigreeFunction三个变量的重要性较大,分值均在18分以上,故在糖尿病的预防及诊断过程中要特别关注这3个特征变量的情况。

3 结论和建议

分析了决策树C4.5、决策树CART、Bagging、随机森林及Adaboost等5种算法在糖尿病预测中的表现,发现决策树C4.5将30名未患糖尿病的人错分成了糖尿病患者,还有131名糖尿病患者没有识别出来;决策树CART将44名未患糖尿病的人分成了糖尿病患者,还有88名糖尿病患者没有识别出来;Bagging算法只将1名未患糖尿病的人错分成了糖尿病患者,只有8名糖尿病患者没有识别出来;随机森林算法及Adaboost算法则全部分类正确。这5种树模型的分类预测错误率分别为20.96%、17.19%、1.17%、0%、0%,从总体上看,3种决策树组合分类模型皆优于单一的决策树分类预测模型,证实了决策树组合模型在糖尿病分类预测中的优越性。选择Adaboost模型找到糖尿病的影响因素相对重要性,发现Glucose、BMI、DiabetesPedigreeFunction 3个变量的重要性较大,故在糖尿病预防及诊断过程中要特别关注这3个特征变量的情况。