一种求解非线性互补问题的非单调光滑牛顿法

王 艳，芮绍平

（淮北师范大学 数学科学学院，安徽 淮北 235000）

0 引言

非线性互补问题(NCP)：求向量x∈Rn，使得

成立。其中，F(x)=(F1(x),F2(x),…,Fn(x))T，且F:Rn→Rn为连续可微函数。

互补问题是计算数学与运筹学的一个交叉研究领域，包括线性、非线性、二阶锥和对称锥互补问题，其中非线性互补问题为最典型，对该问题许多学者提出若干有效算法，包括谱梯度投影法［1］、光滑牛顿法［2-8］、非光滑牛顿法［9］、神经网络法［10］等。其中光滑牛顿法是近年来解决优化问题常用的方法，在文献［2-8］中都利用光滑牛顿法求解NCP(1)，在一定的条件下，证明算法具有全局和局部收敛性。一般在光滑牛顿法中，都是基于单调线搜索来设计求解算法。为提高算法效率，本文将非单调线搜索［11］与光滑牛顿法［12］结合，设计一种新的求解非线性互补问题的非单调光滑牛顿法。在适当的条件下，证明算法的全局收敛性。

1 算法

由文献［14］中的定理3.3知，H(z)在任一点(μ,x)∈R+×Rn处连续可微，其雅可比矩阵为

综上，求解NCP(1)等价于求解H(z)=0。

算法1（非单调光滑牛顿法）

2 收敛性分析

定理2假设{zk} 是由算法1所生成的序列，则当k→∞时，序列{ψ(zk)}收敛于0，且序列{zk} 的任意聚点z*是H(z)=0 的解。

3 数值实验

本节给出3个数值例子来验证算法的有效性。在数值实验中，取参数

算例1令F(x)=Mx+q，其中M=ATA+B，A是n×n的随机阵，它的元素在区间(-5,5)。B是以同样方式产生的随机对称阵。随机向量q在区间(-50,50)服从均匀分布。初始点x0在区间(0,1)随机产生。算法中的μ0为(0,1)上的一个随机数。数值结果如表1。

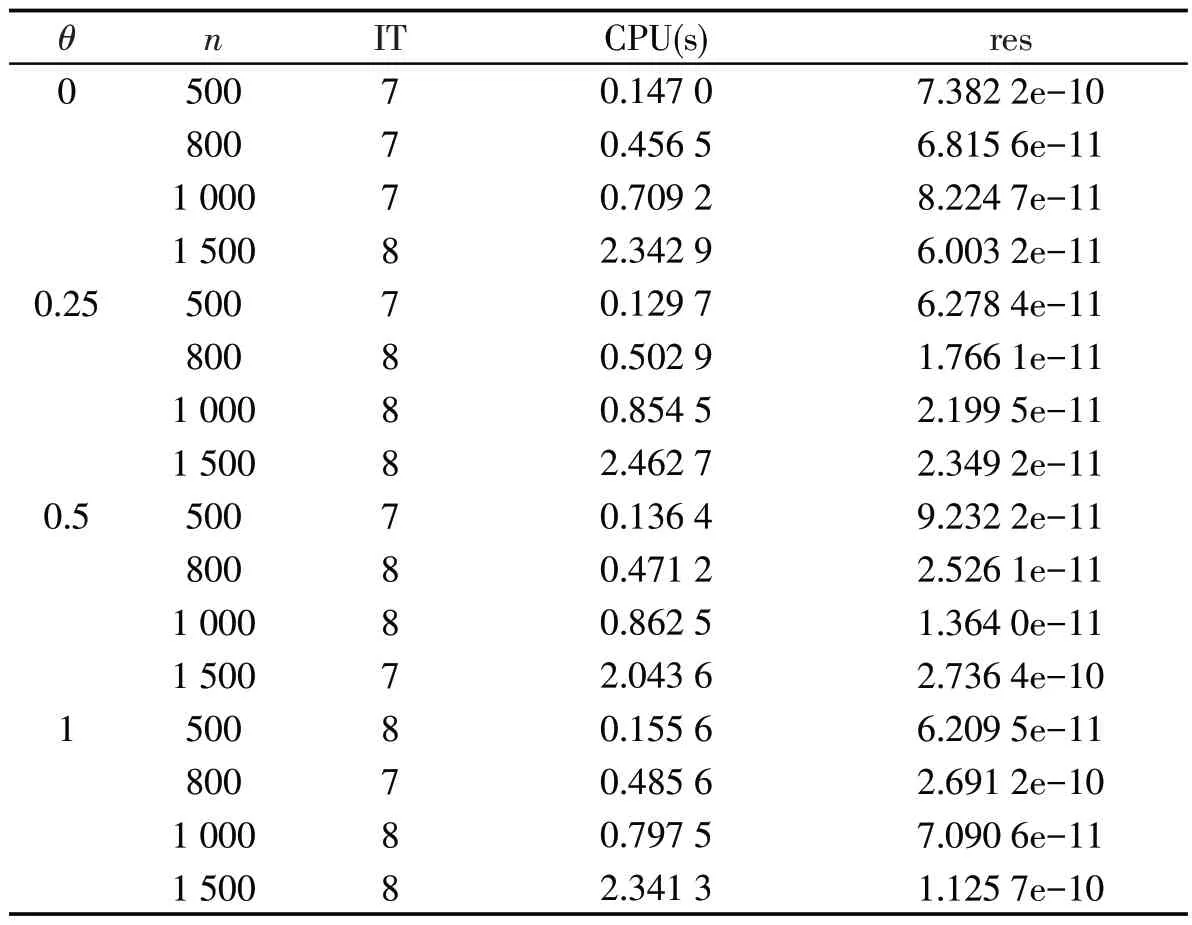
表1 算例3.1的数值结果

算例2［4］令F(x)=D(x)+Mx+q，这里D(x)和Mx+q分别是F(x)的非线性和线性部分，其中矩阵M=ATA+B，A是n×n的随机阵，它的元素来自于区间(-5,5)。B是以同样方式产生的随机对称阵。随机向量q在区间(-50,50)服从均匀分布。非线性部分D(x)的元素Dj(x)arctan(xj)，其中dj在(0,5)上随机产生。初始点x0在区间(0,1)随机产生，算法中的μ0为(0,1)上的一个随机数。数值结果如表2。

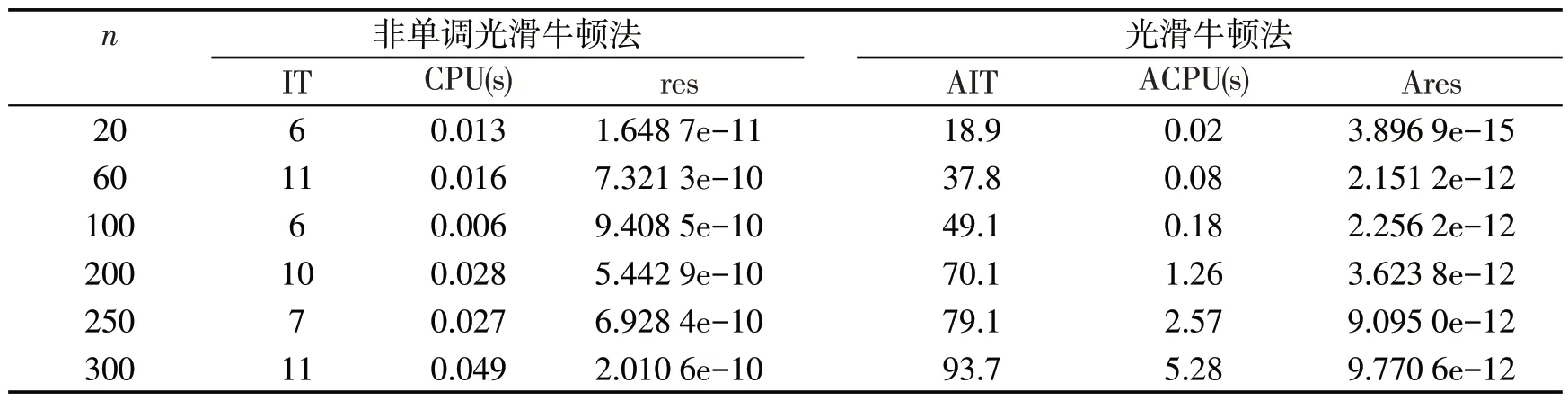
表2 算法1与文献［4］中算法2.1的数值结果比较(θ=0)

算例3［15］（Kojima-Shindo 问题）考虑非线性互补问题，测试函数为

算例1～3的数值实验结果分别列在表1～3中。从表1可以看出，随着增加维数，迭代次数和CPU 运行时间变化微小，表明本文所设计的算法1对求解较大规模互补问题效果较好。在表2中，算法1与文献［4］中算法1相比，所需迭代次数和CPU 运行时间较少，说明算法1求解效率稳定。在算例3中，不同的初始点的计算结果列在表3中，算法1也表现出很好的全局收敛性。

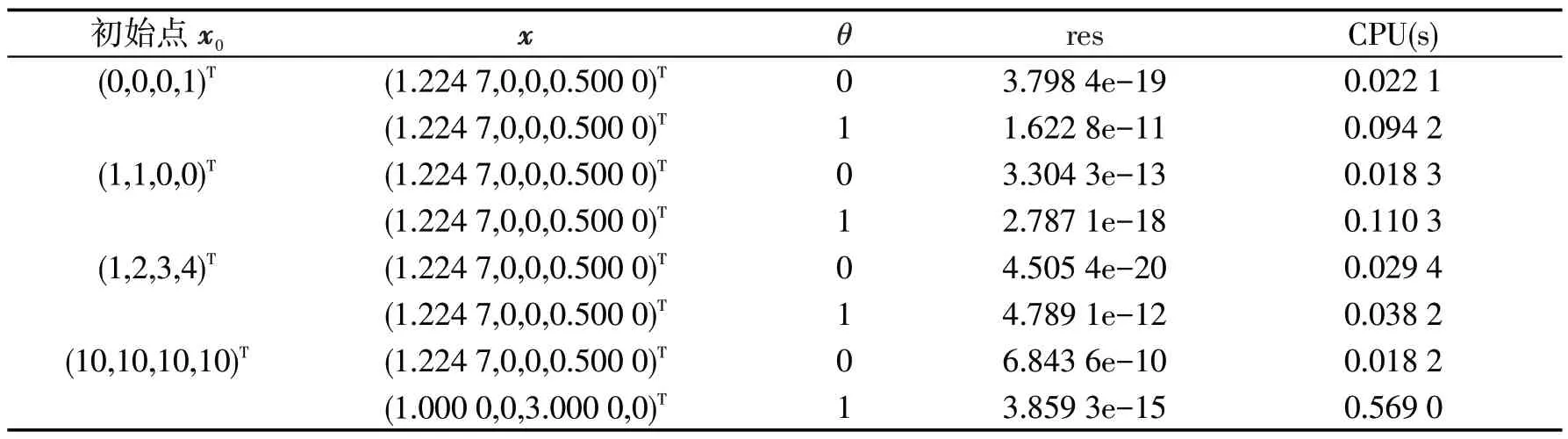
表3 算例3的数值结果

4 结论

本文对非线性互补问题，提出一种非单调光滑牛顿法，数值实验表明算法稳定可靠，且对求解较大规模问题效率较好。算法中Ck的设计作用很大，其表达形式可以进一步优化，后续的研究工作将围绕着Ck的优化展开，以期得到效率更好、收敛速度更快的非单调类算法。