考虑调频性能的风-水-火-储多源调频博弈优化

唐 震,白雪婷,宋述停,董立志,陈 鹤

(1.国网山西省电力科学研究院, 太原 030001; 2.国网山西省电力公司, 太原 030021;3.中国电力科学研究院有限公司, 北京 100192)

0 引言

在当前国家“双碳”战略目标任务的大背景下[1-2],新能源正逐渐高比例集中接入电网。与传统机组相比,新能源发电波动性大,随机性强,由此造成的频率不稳定性给电力系统的安全稳定运行带来重大挑战[3-4]。随着新能源参与发电系统的比例迅速增加,其在能源结构中的比重快速上升,传统的只靠火电机组参与调频的方式已经无法适应高质量的调频需求[5]。

目前,各类型能源机组参与调频的主要研究领域为单机调频。张峰等[6]考虑风电机组参与调频的随机性,构建的风电调频能量联动分配机制能有效提高风电场调频水平,但并未考虑调频的经济特性。刘英培等[7]提出考虑SOC的电池储能系统参与调频的方法,能够将储能电池的荷电状态维持在理想区间的同时保证优良的调频性能,但未研究储能和新能源机组配合参与调频。何廷一等[8]提出一种新型光伏电站最优阵列重构模型,减小了功率调节偏差。李世明等[9]研究了在满足电网频率需求的前提下,如何解决水电孤网振荡并实现快速调频,对水电孤网参与电网调频有重要价值。黄思林等[10]给出了一种火储联合调频方案,采用的高压级联拓扑机构有助于提高综合调频性能,但同样未考虑调频的成本及利润。杨悦等[11]研究了多源联合调频,最小化了调频偏差,但综合调频性能及各调频机组的经济性均未考虑在内。

现有研究大都是针对风、光、水、火、储等各能源机组单独参与电网调频的优化策略进行分析,对于多能源机组共同参与电网调频的协同优化策略研究较少。新能源机组在当前电力系统中正高比例渗透,随机性加剧使电网频率的稳定性受到极大考验[12]。因此,研究新能源机组与传统机组构成的多源调频系统对电网调频性能的提升具有重要意义。

多源调频系统参与电网调频的关键在于保证系统内部参与者的利益分配公平合理,博弈论可为该类交互决策问题提供参考。基于此,提出一种考虑调频性能指标的多源调频博弈优化模型。首先,风电、水电、火电和储能机组构成的多源调频系统在接到电网调频指令后,灵活调整各机组出力协调完成调频过程;然后,对于合作联盟获取的调频利润采用Shapley值法进行初步分配;最后,在Shapley值法的基础上,提出一种采用熵值法将调频性能标准值与调频容量标准值综合加权决定的收益分配系数来改进Shapley值的分配结果。在合作博弈下,采用改进Shapley值法的分配策略能使分配结果更为公平合理。

1 多源联合调频系统框架

当发生负荷扰动时,电网的频率稳定会受到直接影响,此时多源联合调频系统调度中心会根据负荷侧的变动情况测算出调频指令需求,同时将调频需求分配给参与调频的各能源机组(见图1)。在合作博弈[13]模式下,其调度中心会本着联盟系统利益最大化的原则进行调频指令分配。

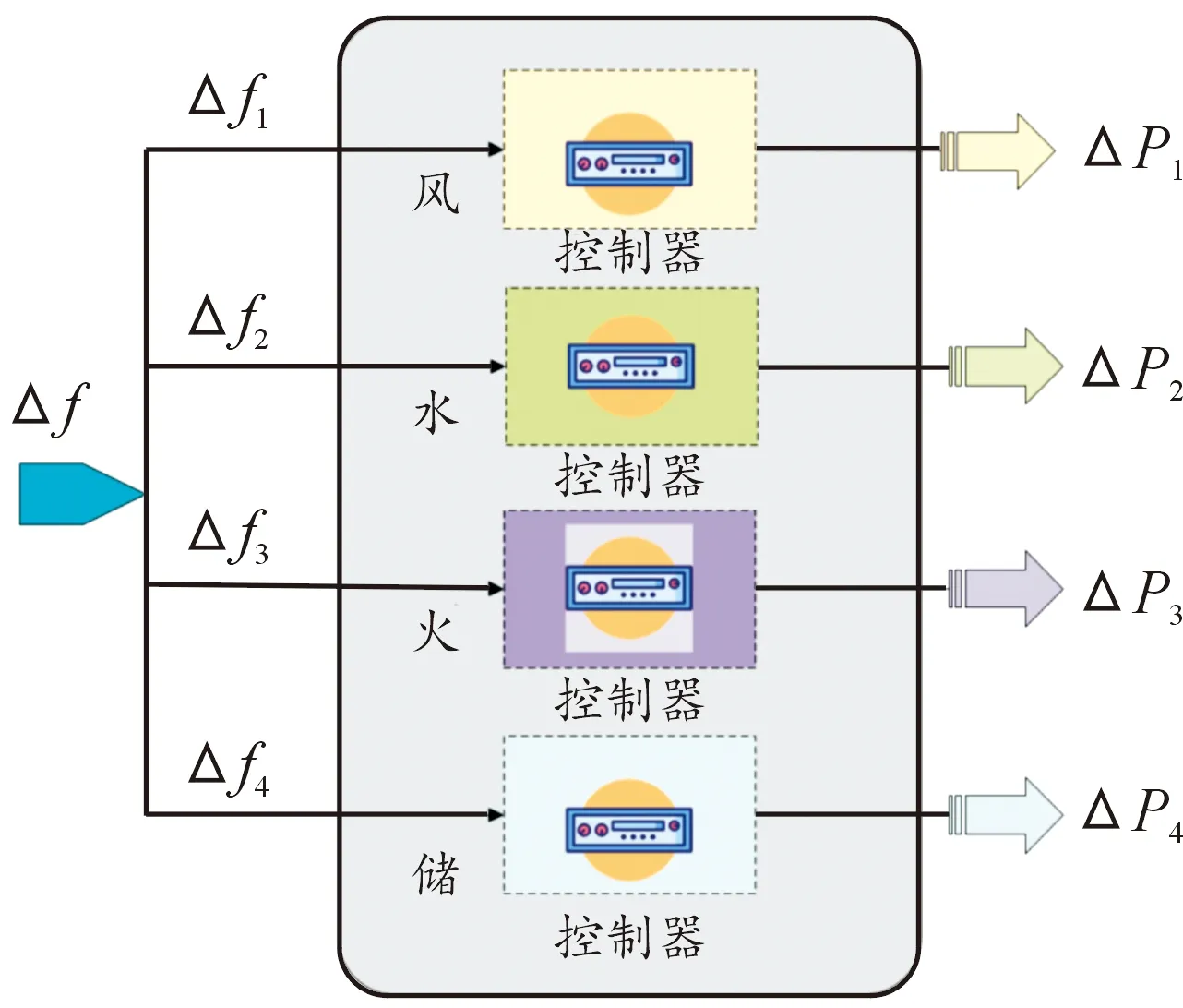
图1 多源联合调频系统框图

当风电、水电、火电、储能机组形成合作联盟系统时,多源调频系统从系统收益最大的原则出发,灵活调整各自出力,从而保证整体收益提升。在非合作模式下,各机组只会根据容量比例分配出力,虽然在满足电网调频指令的同时也能获取一定收益,但是无法本着系统收益最大的原则进行出力的灵活调整,无法保证多源调频系统整体的经济性。因此,在合作联盟的运行机制下,各联盟成员在确保完成调频任务的前提下可实现各主体机组效益最大化[14]。

2 调频性能指标

调频性能指标是各机组参与AGC调频能力的重要参考。我国电力辅助服务市场在“两个细则”的指导下对调频机组考核,调频机组的调频性能取决于机组响应电网调频指令的能力,其综合性能指标取决于以下3项分调频性能指标,分别为调节速度、调节精度与响应时间[15]。

1) 调节速度。反映机组执行调频指令速度的指标,其表达式为

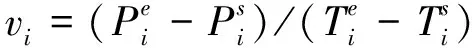
(1)

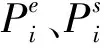
反映机组调节速度指标的表达式为

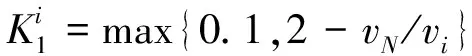
(2)

式中:vN为机组的标准调节速度(MW/min)。

由式(1)和式(2)可知,机组的调节速度指标随机组调节速度的加快而增大,其呈正相关性。

2) 调节精度。反映机组接收的调频指令和执行的调频指令之间的偏差程度,为机组在达到目标调频指令过程中各时刻偏差量的积分,表达式为

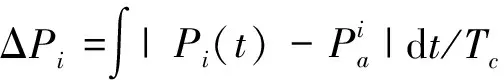
(3)

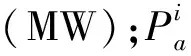
反映机组调节精度指标的表达式为

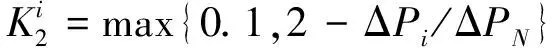
(4)

式中:ΔPN为机组的标准调节偏差,一般为额定功率的1%(MW)。可知,机组的调节精度指标随机组调节过程中调节偏差的减小而增大,其呈负相关性。

3) 响应时间。反映机组接收调频指令的延迟时间偏差。反映机组响应时间指标的表达式为

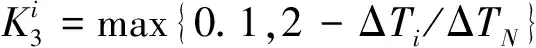
(5)

式中:ΔTi为机组响应指令i的响应时间(s);ΔTN为机组的标准响应时间(s)。

4) 综合调频性能。通过上述3个分调频性能指标可得调频机组的综合调频性能指标,其表达式为

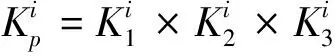
(6)

机组执行N次调频指令后的综合调频性能指标可表示为

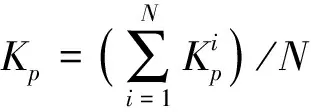
(7)

综上可知,机组的综合调频性能指标越大,其机组调频效果越好。

3 合作博弈下多源调频运行模型

现实中,风电、水电、火电等各发电机组一般为不同的利益方。在非合作运营模式中,各方会注重个体理性,本着个体利益最高的原则参与辅助服务市场调频,不会考虑其余各方收益。在合作运营模式中,各方会通过协议形成合作联盟,各参与者通过合作争取联盟整体的最大利益,其联盟内部的利益分配机制即属于协议内容。本文考虑的便是合作博弈下的风电、水电、火电以及储能机组的运行经济性问题。

3.1 合作联盟构成

在一定的规则条件下,拥有绝对理性的各决策方制定策略方案,并付诸行动,在行为过程中获取相应利益的过程即为博弈。在参与电网AGC调频任务中,多源调频系统中的各个电源作为决策者,在某种约定的协议下组成合作联盟共同完成电网调频指令需求,联盟内部成员按照协议约定的利益分配机制进行联盟总收益的分配,运营框架见图2。因此,本文采用合作博弈来探究各发电机组间的合作调频方式。

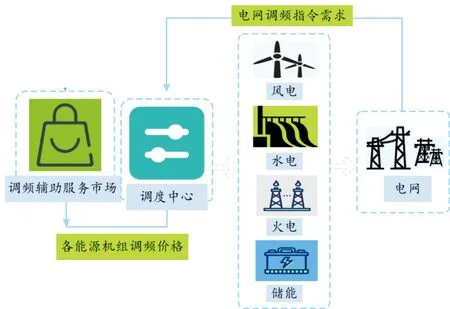
图2 合作联盟多源调频系统运营框架

存在合作联盟博弈的2个基本原则[16]为:

1) 群体理性原则:即对参与调频的联盟整体而言,在合作联盟的运行机制下,联盟整体收益要大于各方单独运行时收益之和。

2) 个体理性原则:即对参与调频的联盟各方而言,按照联盟内部的利益分配机制获取的收益要大于联盟各方单独运行时获取的收益。

联盟合作原则为:

1) 风电、火电、水电、储能机组参与合作联盟时,可彼此考虑对方收益,灵活调整各自发电量,追求合作整体的利益最大化,而不是自身利益最大。

2) 若未参与联盟,各主体之间只会根据容量比例分配系统调频任务,不会考虑系统整体的利益最大化。

3.2 约束条件

考虑调频系统约束和各类型机组调频约束。

1) 系统约束。系统调频容量约束为

RW+RH+RT+RES=RS

(8)

式中:RW、RH、RT、RES为风电、水电、火电、储能的调频容量;RS为系统所需的调频容量。

系统调频里程约束为

LW+LH+LT+LES=LS

(9)

式中:LW、LH、LT、LES为风电、水电、火电、储能的调频里程;LS为系统所需的调频里程。

LS≤sRS

(10)

式(10)中,s为多源调频系统的历史调频里程调用系数,该值为历史经验值,为过去一段时间内系统内总调频里程与总调频容量的比值,其物理意义为系统内部单位调频容量所需的调频里程。

系统爬坡速率约束为:

vW+vH+vT+vES≥vS

(11)

式中:vS为系统所需的爬坡速率;vW、vH、vT、vES为风电、水电、火电、储能的爬坡速率。

2) 风电机组调频约束。调频容量约束为

RWmin≤RW≤RWmax

(12)

式中:RWmin、RWmax为风电机组出力的上下限。

调频里程约束为

LW≤sWRW

(13)

式中:sW为风电机组历史调频里程调用系数。

3) 水电机组调频约束。调频容量约束为

RHmin≤RH≤RHmax

(14)

式中:RHmin、RHmax为水电机组出力上下限。

调频里程约束:

LH≤sHRH

(15)

式中:sH为水电机组历史调频里程调用系数。

4) 火电机组调频约束

调频容量约束:

RTmin≤RT≤RTmax

(16)

式中:RTmin、RTmax为火电机组出力上下限。

调频里程约束为

LT≤sTRT

(17)

式中:sT为火电机组历史调频里程调用系数。

5) 储能电站调频约束。调频容量约束为

RESmin≤RES≤RESmax

(18)

式中:RESmin、RESmax为储能电站出力上下限。

调频里程约束为

LES≤sESRES

(19)

式中:sES为储能电站历史调频里程调用系数。

功率约束为

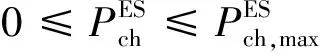
(20)

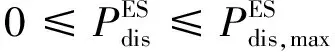
(21)

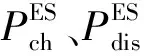
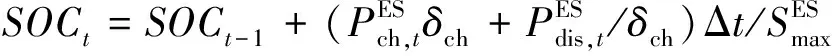
(22)

0.2≤SOC≤0.8

(23)

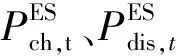
各类型机组运行参数见表1。

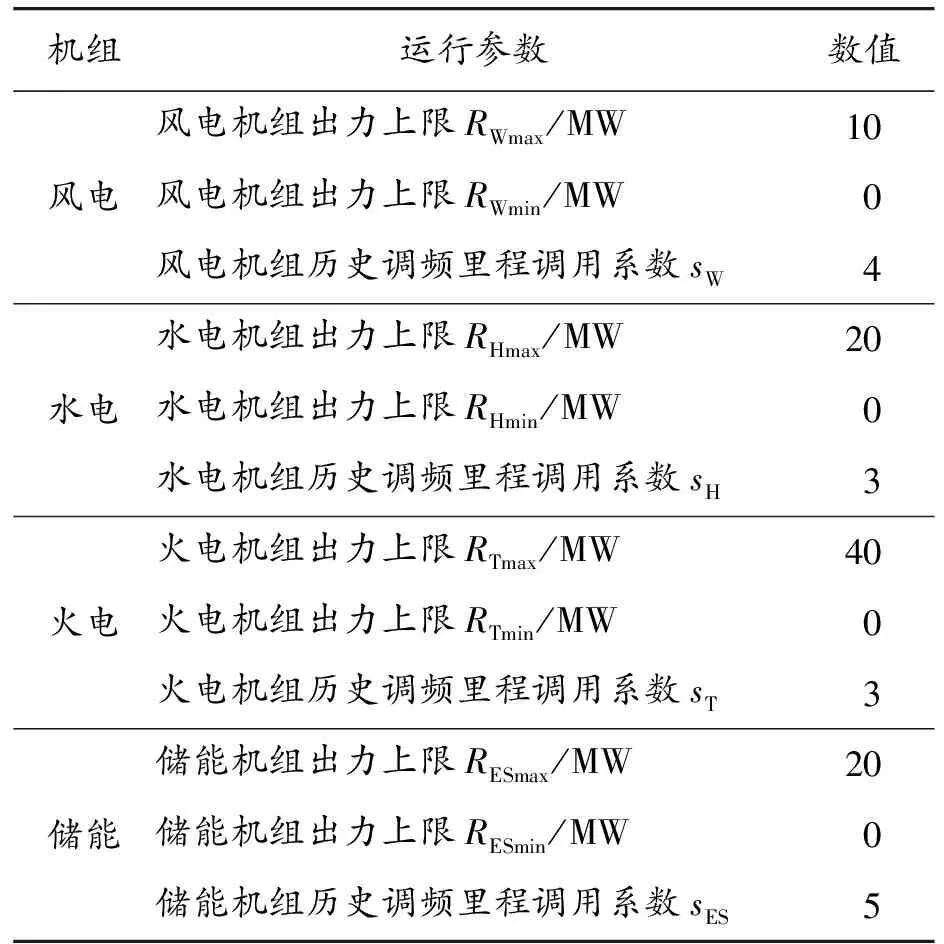
表1 各类型机组运行参数

3.3 优化目标

多源调频系统的总收益为风、水、火、储4种类型机组参与调频的收益之和。以多源调频系统总收益最大为优化目标,建立目标函数如下:

max{kW(qWRW+pWLW)+

kH(qHRH+pHLH)+

kT(qTRT+pTLT)+

kES(qESRES+pESLES)}

(24)

其中:kW、kH、kT、kES分别为风电、水电、火电、储能的调频性能指标;qW、qH、qT、qES分别为风电、水电、火电、储能的调频容量价格;pW、pH、pT、pES分别为风电、水电、火电、储能的调频里程价格。

3.4 合作博弈的Shapley值分配模型

Shapley值法[17]是在合作博弈获取最大利益后按照各方贡献度进行利益分配的一种策略,它可以分析参与方对总收益的贡献度并按照各方贡献价值进行分配,保证分配结果的公平性。这种分配策略可用来解决联盟各方在合作过程中的利益分配问题,图3给出了基于合作博弈Shapley值的分配流程。

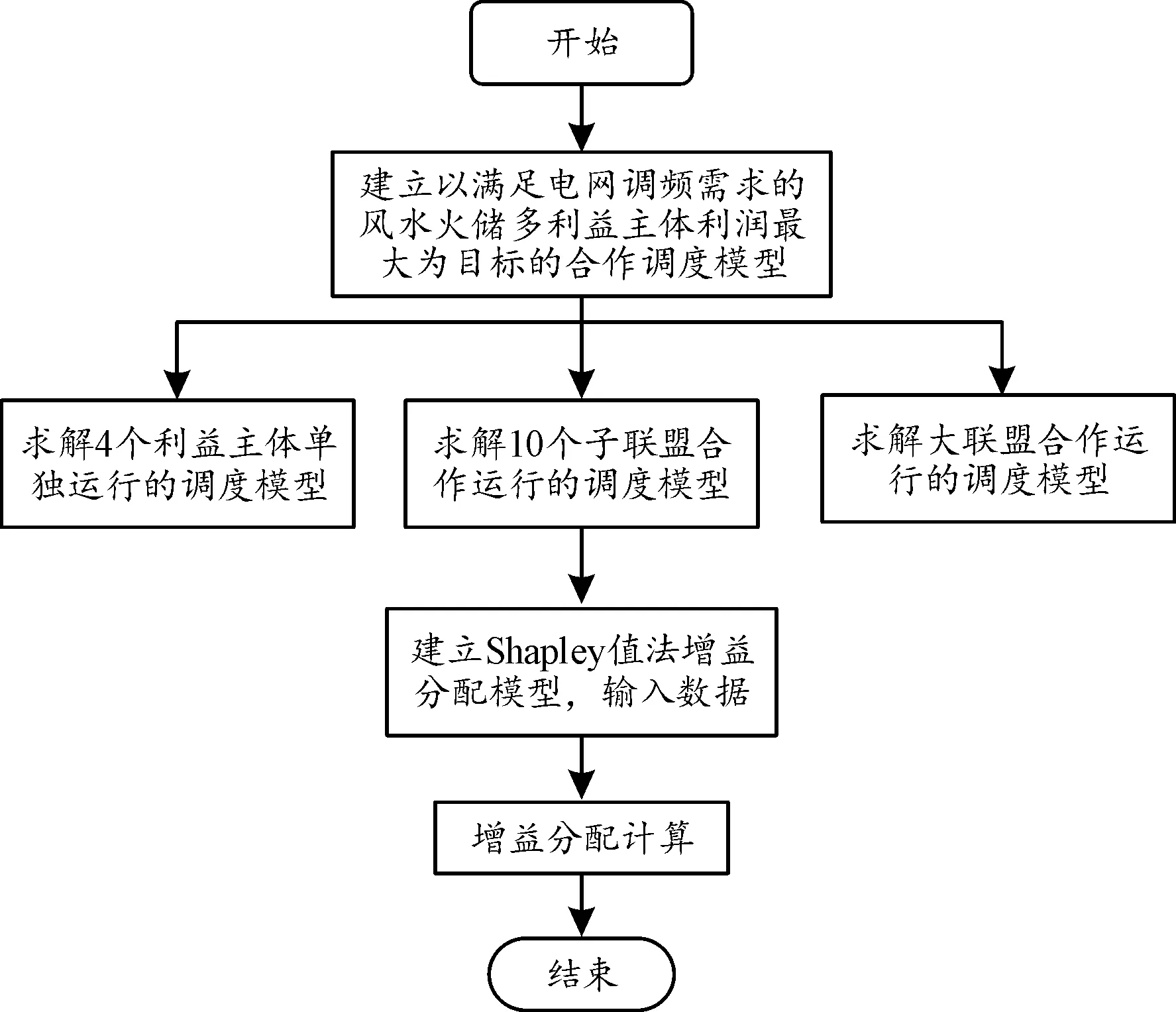
图3 基于合作博弈Shapley值的分配流程

根据Shapley值理论,收益分配为:

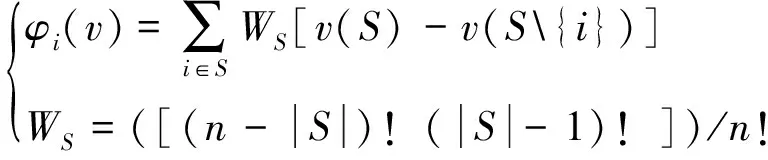
(25)

式中:φi(v)为成员i的收益分配方案;v(S)为联盟S的收益;v(S)-v(S{i})为成员i参与各方联盟S时所创造的贡献值;WS为加权因子,即成员i对于联盟整体而言应获得的利益权重。

3.5 合作博弈的改进Shapley值分配模型

3.5.1 考虑调频性能指标的收益分配系数

在Shapley值法下,根据各发电主体对调频容量的贡献程度进行利益分配,满足电网调频需求。在此基础上,改进的Shapley值法[18]考虑各发电机组的调频性能情况进行收益的再分配,激励各发电机组达到电网调频容量需求后继续改善综合调频性能值,提升调频质量,有利于联盟主体适应未来电力市场环境。收益分配系数C体现各调频机组的调频性能情况,调频性能K值越大,联盟系统的综合调频性能Kave值就会越大,系统的调频质量就会越好。设各发电机组i的调频性能标准值为CK,i,可得CK,i的计算式为:

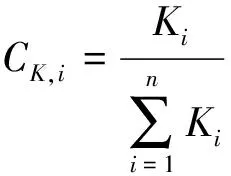
(26)

收益分配系数C还与各发电机组提供的调频容量有关,提供调频容量占比高的成员对联盟系统带来的影响也更大。设各发电机组i的参与调频容量标准值为CR,i,可得CR,i的计算式为:

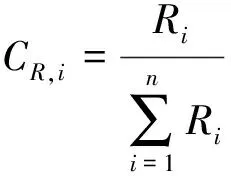
(27)

设CK,i和CR,i的对应权重为ω1和ω2,可得收益分配系数Ci为:

Ci=ω1CK,i+ω2CR,i

(28)

ω1和ω2之和为1。采用熵值法计算两者之间的权重。若有n个发电机组,m个影响指标,则指标矩阵可表示为:

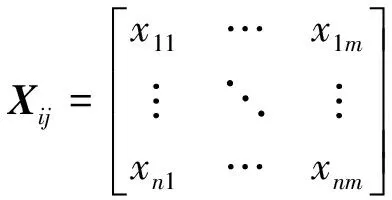
(29)

(30)

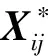
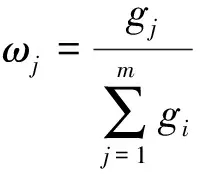
(31)

其中,gj=1-ej;ωj的取值在0到1之间。

3.5.2 改进Shapley值法

得到收益分配系数后可对Shapley值法得到的分配结果进行改进再分配。改进Shapley值法的修正系数为收益分配系数Ci,修正系数向量可表示为C=[C1,C2,…,Cn],其中n为联盟主体的成员个数。各发电机组的修正因子ΔCi可表示为:

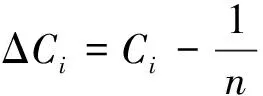
(32)

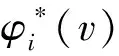
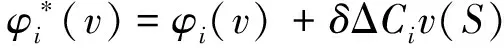
(33)

根据改进的Shapley值法再分配的收益结果结合了Shapley值和C值,考虑机组参与调频容量的同时又考虑了各机组的调频性能,使得收益的再分配结果更加客观、公正。

4 算例分析

探究多类型机组共同参与电网调频的综合协调优化策略,验证改进合作博弈模式的优越性。首先,选取具有代表性的风、水、火、储机组构成多源调频系统混合整数线性规划模型,该模型由 Matlabr 2014a中的CPLEX进行求解,通过对系统多种运营模式下的经济性对比获取最优运营模式;其次,由系统到个体,获取系统最优运营模式后,对改进Shapley值法进行参数的深入分析,同时对改进Shapley值法在系统最优运营模式下的个体进行经济性分析;最后,对比分析了系统在最优运营模式下的调频性能。

4.1 调频市场

为验证合作联盟调频系统的有效性,采用山西调频辅助服务市场对调频系统协调控制策略进行研究,表2为风电、水电、火电、储能机组的调频信息[19]。

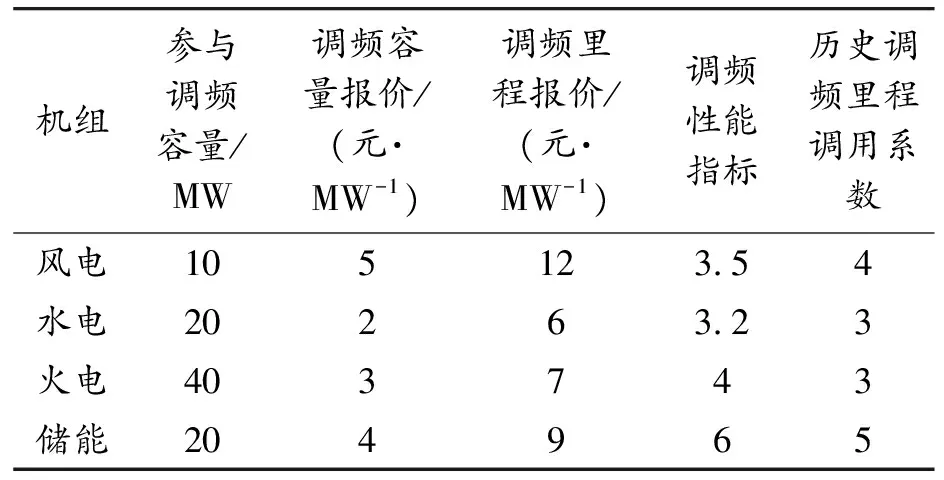
表2 不同类型电源的调频信息

4.2 多源调频模式

为分析多源调频系统在合作博弈模式下运行的经济性,考虑4种类型机组所有合作模式下系统运行的收益情况,共计12种运营模式,包括非合作模式,合作模式以及10种部分合作模式,表3列举了各种运营模式场景。

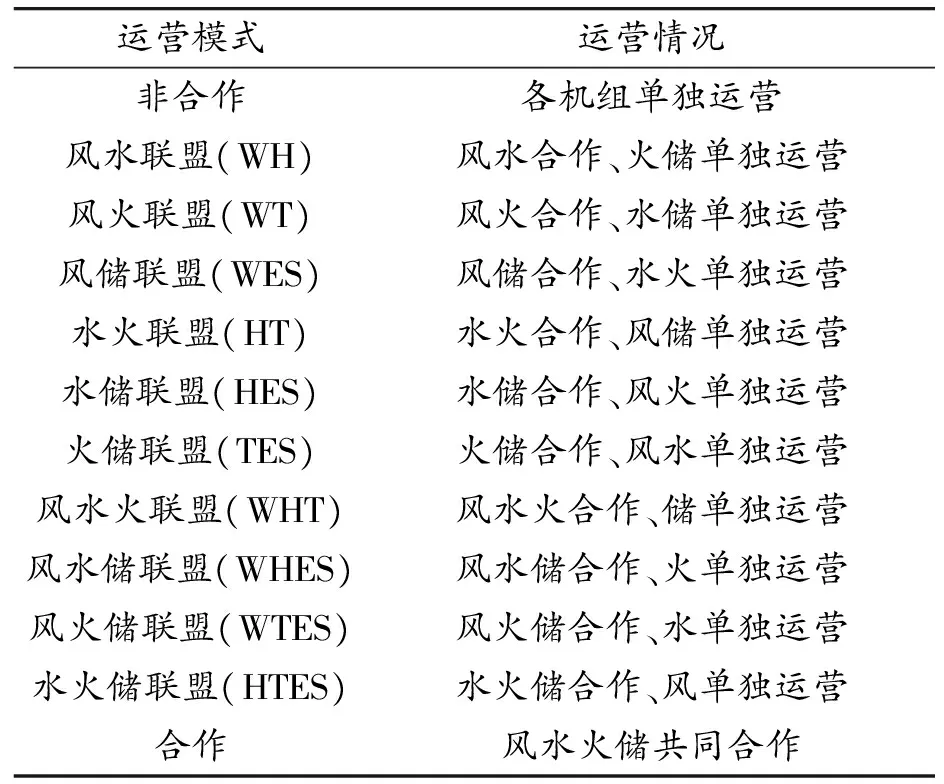
表3 运营模式设置

将多源调频机组参与电网调频调度周期的仿真运营模式需求设置为:调频容量需求为45 MW,调频里程需求为135 MW。

4.3 运行结果分析

4.3.1 合作模式的经济最优性验证

为验证多源调频系统在合作模式下的经济性最优,对表3中列举的各类运营模式的系统总收入作对比分析,图4给出了各运营模式下多源调频系统的收益情况。

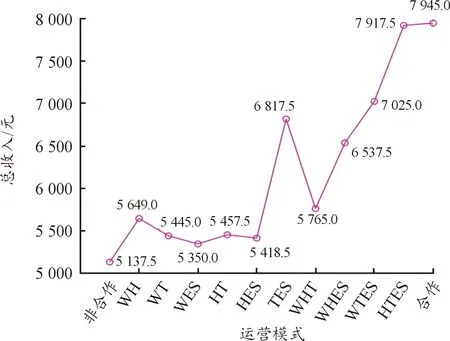
图4 各运营模式下多源调频系统的总收入

由收益数据明显可见,多源调频系统在非合作运营模式下系统收入最低,部分合作运营模式次之,合作模式下系统总收入最高。其中对于部分合作模式的运营情况进行分析,可以看出相比于两种类型机组合作,3种类型机组合作下的运营模式一般会使得系统收入更高。究其原因是参与合作的机组宁肯牺牲个体利益也会坚持系统利益最优的原则,因此越多机组参与合作模式,系统的灵活性便会越高,从而产生更大的合作剩余,使得系统总收入更高。相较于机组单独或部分合作的运营模式,多源调频系统在合作模式下的系统调频收益最高。

4.3.2 基于改进Shapley值的收益情况分析

对比分析12种运营模式下系统的收入情况,可知多源调频机组的合作模式为系统经济性最优的运营模式。当多源调频系统获取了最优的运营模式后,接下来便要考虑各主体机组的利益分配问题。

上文中已提到再分配调节系数δ的值可根据实际合作情况确定,从而影响改进Shapley值的作用程度,表4给出了δ值分别为0.08、0.10、0.12下的改进Shapley值分配情况。

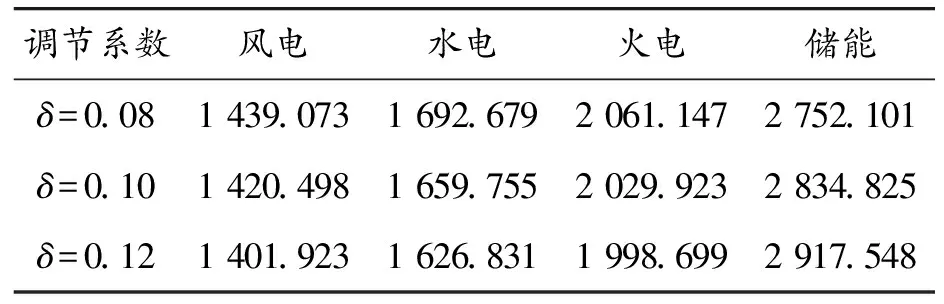
表4 不同调节系数下改进Shapley值分配情况

对表4中的数据进行可视化处理,不同调节系数下改进Shapley值分配情况见图5。

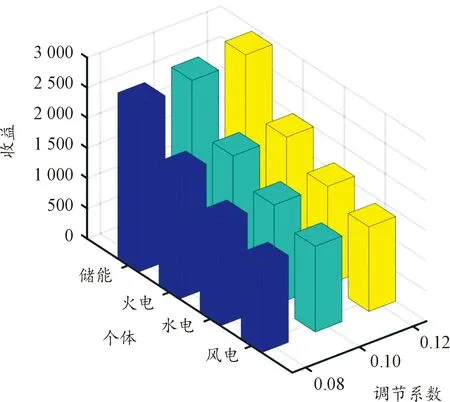
图5 不同调节系数下改进Shapley值分配情况直方图

综合表4、图5数据可知,各主体机组的收益会随着再分配调节系数δ的值的变化进行等比例调整,从而影响收益分配系数C的作用程度。收益分配系数由调频性能标准值与调频容量标准值综合加权决定,因此系统决策者可根据实际情况需要确定δ的取值,从而得到使各方满意的更为公平合理的再分配结果。

基于熵值法下的改进Shapley值理论,得到各能源主体机组的收益分配系数和修正因子,见表5。

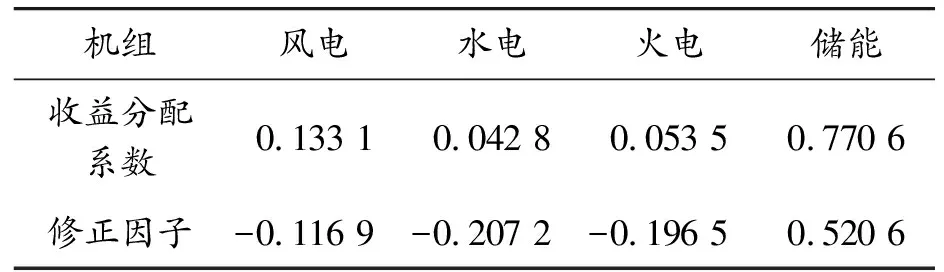
表5 改进Shapley理论下的参数

决策者虽然可根据实际情况确定δ的取值,但前提条件是要保证各机组合作后的收益要高于非合作时的收益,才能确保合作模式的运营机制。选取δ值等于0.1时的再分配结果为例,对Shapley值的改进效果进行分析。

为了更好地展示改进Shapley值的收益分配结果,对表6数据进行了图示化处理, 改进Shapley值前后各主体机组收益情况见图6。

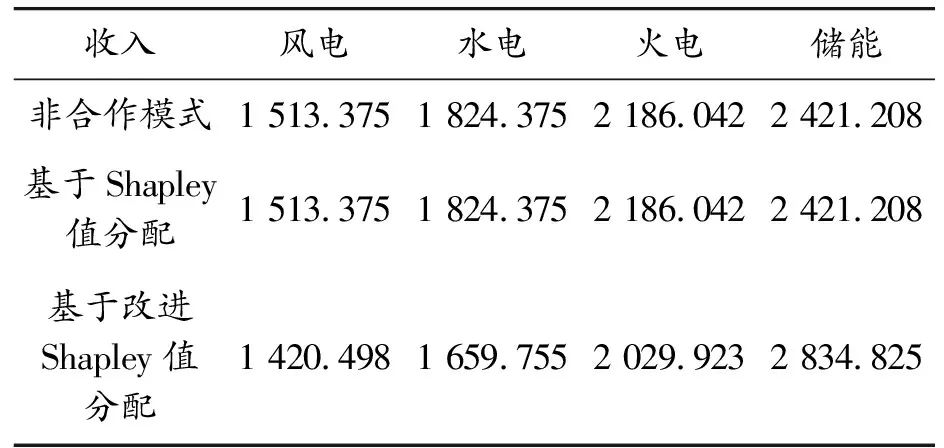
表6 改进Shapley值前后各主体机组收益情况

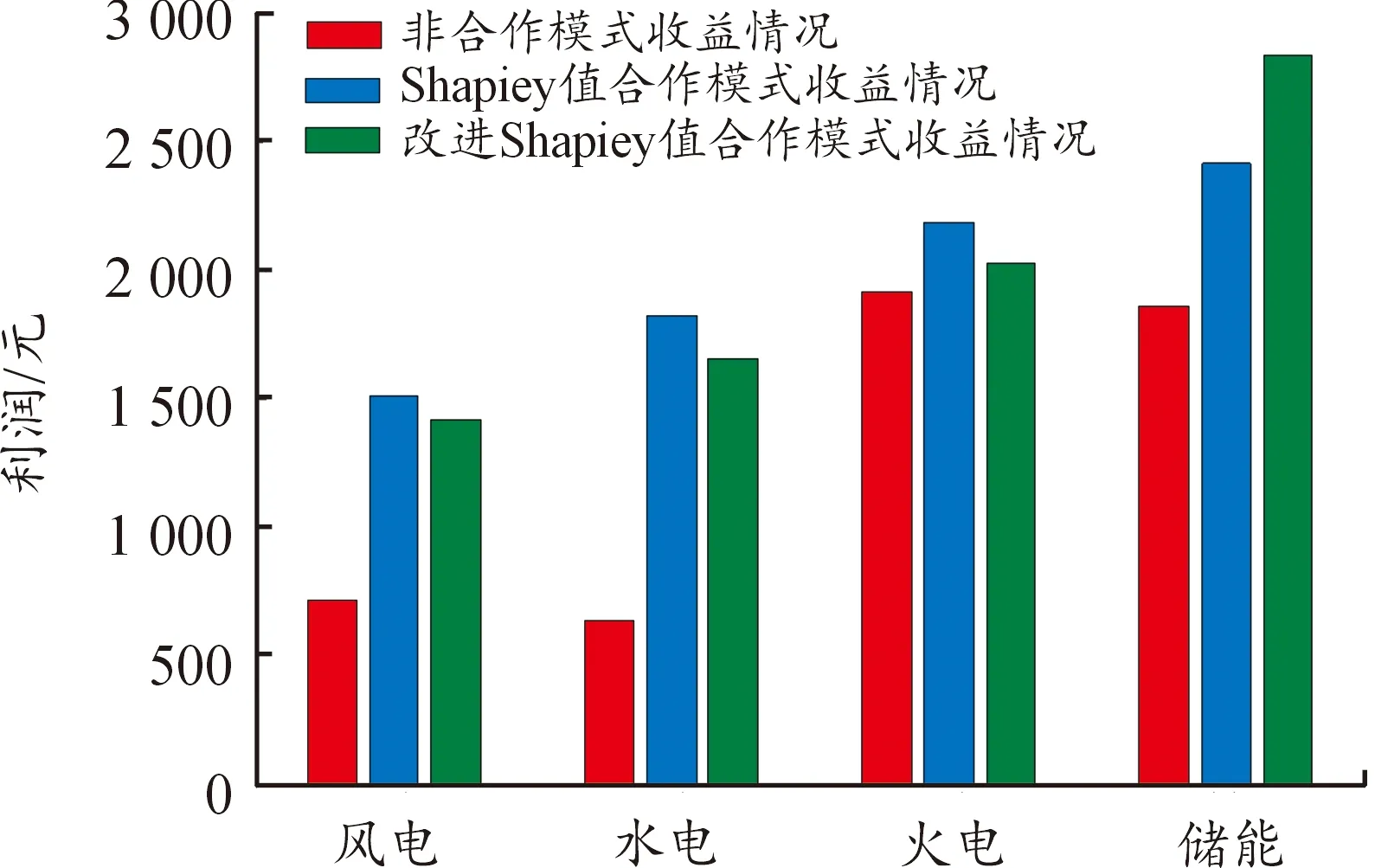
图6 改进Shapley值前后各主体机组收益情况

给出采用Shapley值法和基于熵值法改进的Shapley值法的两种收益分配结果。为增强各类型主体机组参与合作联盟的意愿,同时给出了各类型机组非合作(即单独运营)时的收益情况。

综合表6、图6的数据可知,基于Shapley值改进前后的合作模式下各主体机组的收益都高于非合作模式下的收益。因为系统在合作模式下,满足电网调频需求后,会本着整体最大收益的原则灵活调整各机组出力,剩余利益根据Shapley值法按照贡献率分配,因此各主体机组的收益都会提高,从而提高各类型机组参与合作模式的积极性。另外,对比改进Shapley值前后各主体机组收益情况可知,风电、水电、火电的收益分别少了92.877元、164.62元、156.119元,而储能的收益增加了413.617元。由此可见,改进Shapley值法下调频性能最好的储能机组的收益有所提高,原因是此时引入的收益分配系数考虑了机组的调频性能指标,其再分配结果使得调频性能较为优良的机组能获得较高的收益。此时的合作分配机制更为公平合理,有利于维持和电网长期的合作关系。

4.3.3 合作模式下的调频性能分析

在给定调频需求下,根据各主体机组的出力比例,加权求得系统的综合调频性能。其中合作模式下调频性能指标的加权平均值为5.72,非合作模式下该值为4.2,由此可见,所提出的合作博弈下的调频性能指标明显优于各机组单独运营参与调频时的调频性能。因此,多源调频系统合作模式下能够在有效响应电网调频需求指令的同时,更有利于电网频率的稳定性,从而提升各主体机组在调频辅助服务市场参与电网调频时的竞争力。

5 结论

1) 仿真了合作模式、非合作模式以及10种部分合作模式下风-水-火-储多源调频系统的运营收入,合作模式下系统的总收入最高,部分合作模式下次之,完全非合作模式下系统利润最低,验证了合作模式为多源调频系统最优的运营模式。

2) 对于合作模式下各主体机组的利益分配,在Shapley值的基础上考虑收益分配系数进行了改进。改进的Shapley值分配策略综合考虑了调频性能与调频容量,使得合作博弈模式下的分配机制更为公平合理,从而激励各机组能够维持长久的合作关系。

3) 建立的多源调频博弈优化运行模型在寻求系统利益最大化及利益分配策略上均考虑了调频性能指标,因此,合作博弈模式下系统的综合性能指标加权平均值有较大幅度提高,调频的综合性能指标更加优良,从而提升各类型机组参与调频辅助服务市场的竞争力。