基于收益塑造技术的知识图谱多跳推理

姚章俊

(西南电子技术研究所 第四事业部，四川 成都 610036)

0 引 言

知识图谱以结构化的形式描述客观世界中概念、实体及其之间的关系，多跳推理接受实体及关系等查询条件，根据特定算法计算出起始实体满足关系映射的目标实体[1]。举例说明：图1展示部分新冠疫情知识图谱，其中包含多个已知的事实三元组，如 ("药物"，"治愈"，"疾病")、 ("病毒"，"变异"，"基因") 和 ("防疫方案"，"圈定"，"聚集区") 等，知识图谱多跳推理用以推断与“防疫方案”为“包含”关系的目标实体(在图1中是“中药”)，与“个人”为“感染”关系的目标实体(在图1中是“病毒”)。

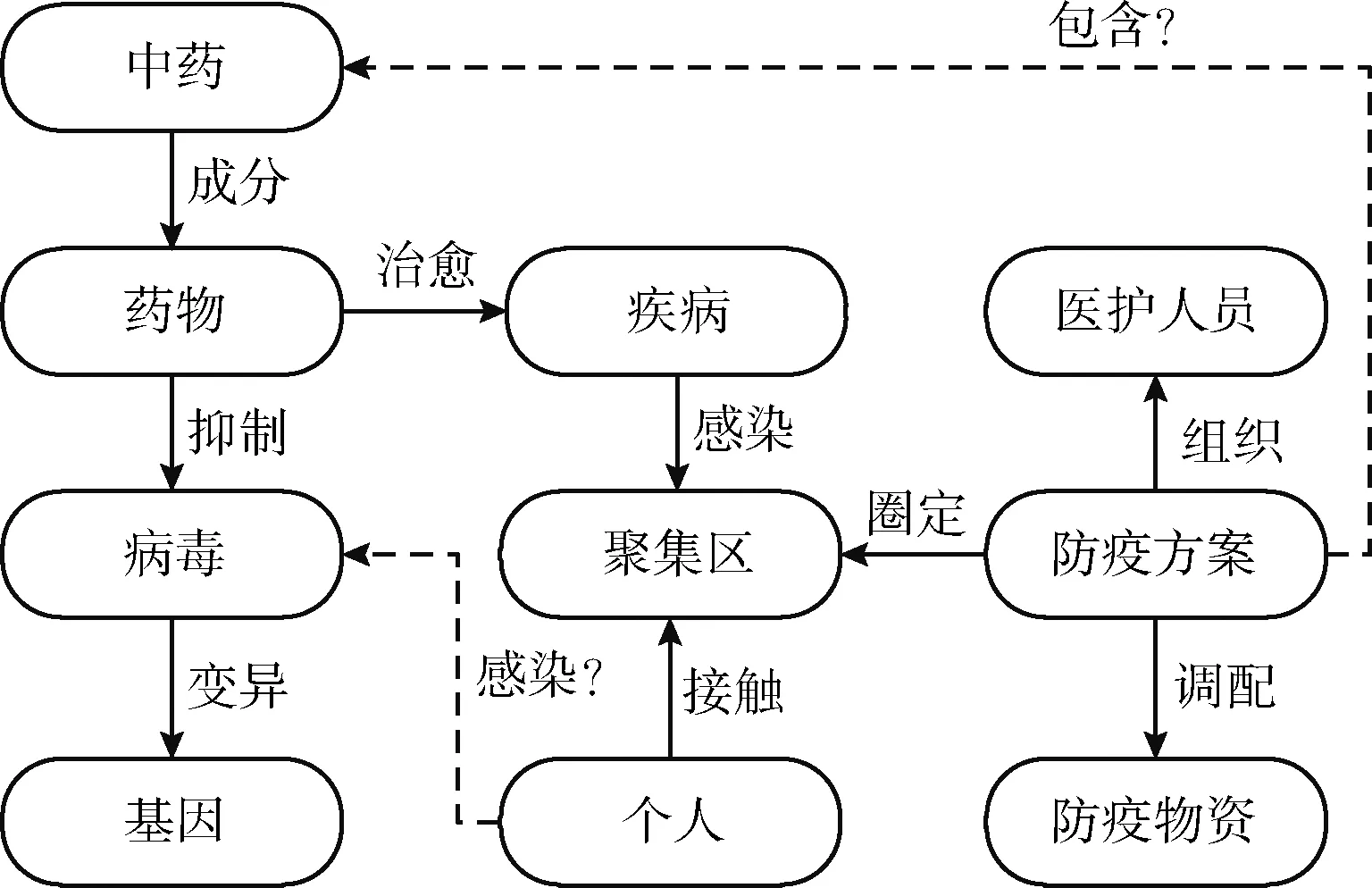
图1 新冠疫情知识图谱多跳推理示例

在现有多跳推理方法中，文献[2]中基于描述逻辑推理方法和基于本体规则推理方法具有规则编写复杂、冲突消解困难、泛化能力差的缺点；文献[3]基于分布式嵌入表示推理方法和基于神经网络关系路径推理方法具有可解释性不强，返回结果可信度低，且无法在大规模知识图谱上应用的不足。

综合国内外文献[4-9]可知，知识图谱多跳推理可以被建模为有限视界的确定部分可观测马尔可夫决策过程，满足强化学习试错和延迟收益的特点：从起始实体开始，在推理智能体与知识图谱环境不断交互中，每一步选择一条关系边，以最大化收益期望为目标，不断搜索推理路径直至满足查询关系映射的答案节点。期间不需要访问任何预计算的路径，也不需要对候选路径进行排序，避免在海量知识图谱上出现维度灾难问题。笔者认识到知识图谱的图结构即包含拓扑信息又包含语义信息，对知识图谱拓扑信息做图卷积操作，对比现有知识图谱表征学习算法，能够获得更加丰富的意含表征。基于此笔者提出基于深度图强化学习多跳推理算法DRL-MHR。

相较现有基于强化学习的知识图谱多跳推理算法，DRL-MHR算法具有较多优势：第一，DRL-MHR能力选择可变长度路径，对于推理链复杂的问题至关重要；第二，DRL-MHR算法作为一种离轨策略梯度学习算法，不需要预训练或微调，不需要从零开始学习策略。

1 相关工作

1.1 知识图谱推理

文献[10-15]指出基于深度学习的知识图谱推理技术包含基于分布式嵌入表示推理、关系路径推理和基于深度强化学习的路径发现等3类，核心都在于学习事实三元组的低维度嵌入和捕获多步关系。文献[16，17]提出的关系路径推理在图结构上利用路径信息建模关系路径，路径排序算法在路径约束组合下选择关系路径，并进行最大似然分类。相较深度学习算法，DRL-MHR通过溯源推理路径解释其预测结果，推理过程清晰可见，不再是不可解释的黑盒。文献[19]中的DeepPath将强化学习应用于关系路径学习中，通过翻译嵌入方法对连续空间中的状态进行编码，并将关系空间作为其动作空间，根据路径多样性和路径效率的奖励功能提高准确性。文献[20]提出MINERVA算法，它通过最大化期望的奖励，将走到正确答案实体的路径作为一个顺序优化问题。文献[21]提出了隐性推理网，在训练数据的嵌入神经网络空间中，隐性推理网根据当前状态向量和从共享内存得到的注意力向量共同产生下一个状态，学习执行多步推理。文献[22]提出了神经逻辑编程，该方法来自于被称为TensorLog的可微逻辑，它将一阶逻辑规则的参数学习和结构学习结合在一个端到端可微模型中，推理任务则被编译成可微操作序列。文献[23]使用收益塑造技术用以改善MINVERVA中的奖励稀疏问题，本文将其作为基线模型，为了叙述方便，笔者将其简写为MHKGR-RS。DRL-MHR在继承前述基于强化学习框架的基础上，使用基于图网络的知识图谱拓扑表征方法，构建出高相关性的语义邻域，使得推理智能体能够在较小范围内高效搜索，平衡推理智能体探索不彻底与利用不充分之间的矛盾。

1.2 深度强化学习推理

在解决高层次深度强化学习任务时，智能体只有具备交互、感知、学习、反馈、进化等能力，才能做出最优的决策。当前深度强化学习推理主要有3类算法：其一，基于记忆网络的深度强化学习模型，通过在传统的DRL模型中加入外部的记忆网络部件RNN，使得模型拥有了一定的记忆和推理能力。文献[24-26]中提出的基于经验回放的深度强化学习、基于记忆网络的深度强化学习算法、基于情景记忆的深度强化学习算法和基于可微分计算机的深度强化学习从不同角度对其优化；其二，将外部知识与深度强化学习结合起来，Lu等[27]通过添加环境特征信息和结合两个决策源增加图像输入，在Microsoft Malmo平台的3D部分可观测环境中与单一强化学习模型相比，实验评估表现出更高的性能和更快的学习速度；其三，将示例视为行为偏差的来源，Bougie等[28]提出了一个以人性化的方式从示例中受益的代理框架。在该框架中，智能体通过观察建立因果模型，并根据这些知识进行推理，以分解任务，实现有效的强化学习。DRL-MHR算法也是一种离轨策略梯度学习算法，不需要预训练或微调，从零开始学习策略。对比上述优秀算法，DRL-MHR能够选择可变长度路径，这对于推理链复杂的问题至关重要。

2 基础知识

为方便查找建模过程中用到的诸多符号，编撰表1便于理解建模思想。为方便使用与阅读，所有的符号遵循这样的规律：大写字母表示该领域，如At表示智能体在时刻t时的动作；花体字母表示该领域的集合，如A表示智能体的行动集合；黑体字母表示对应字母的张量表示形式，如At为At的张量表示形式；小写字母表示该领域在某一时刻的具体取值，如a表示智能体的具体动作值，其它领域符号以此类推。

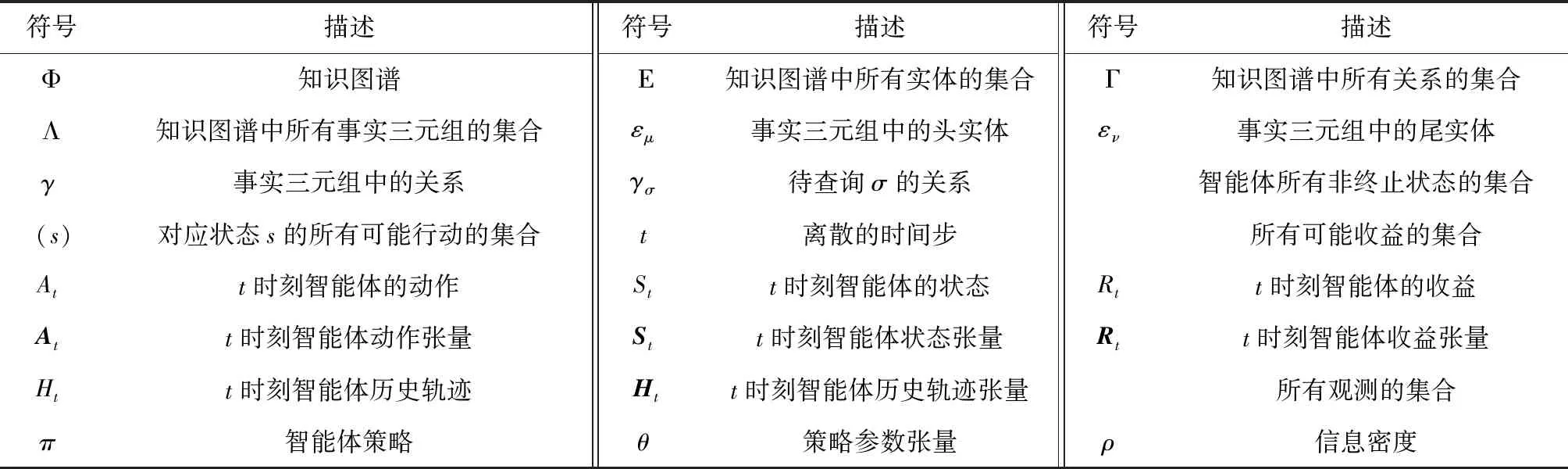
表1 符号

知识图谱工作环境被建模为一个确定的部分可观测马尔科夫决策过程，强化学习是一种通过交互式学习实现目标的理论框架，如图2中显示，推理智能体是学习及实施决策的主体，知识图谱是推理智能体活动的环境。推理智能体根据知识图谱环境的状态和状态转移概率，决定下一时刻跳转的行为路径，知识图谱环境对这些动作依据收益规则，给予推理智能体相应的收益信号，并向推理智能体呈现出新的知识图谱子图状态。知识图谱环境产生的累计收益，就是推理智能体在不断地路径选择探索中需要最大化的目标。知识图谱的强化学习环境被定义为一个五元组 (S，O，A，P，R)。

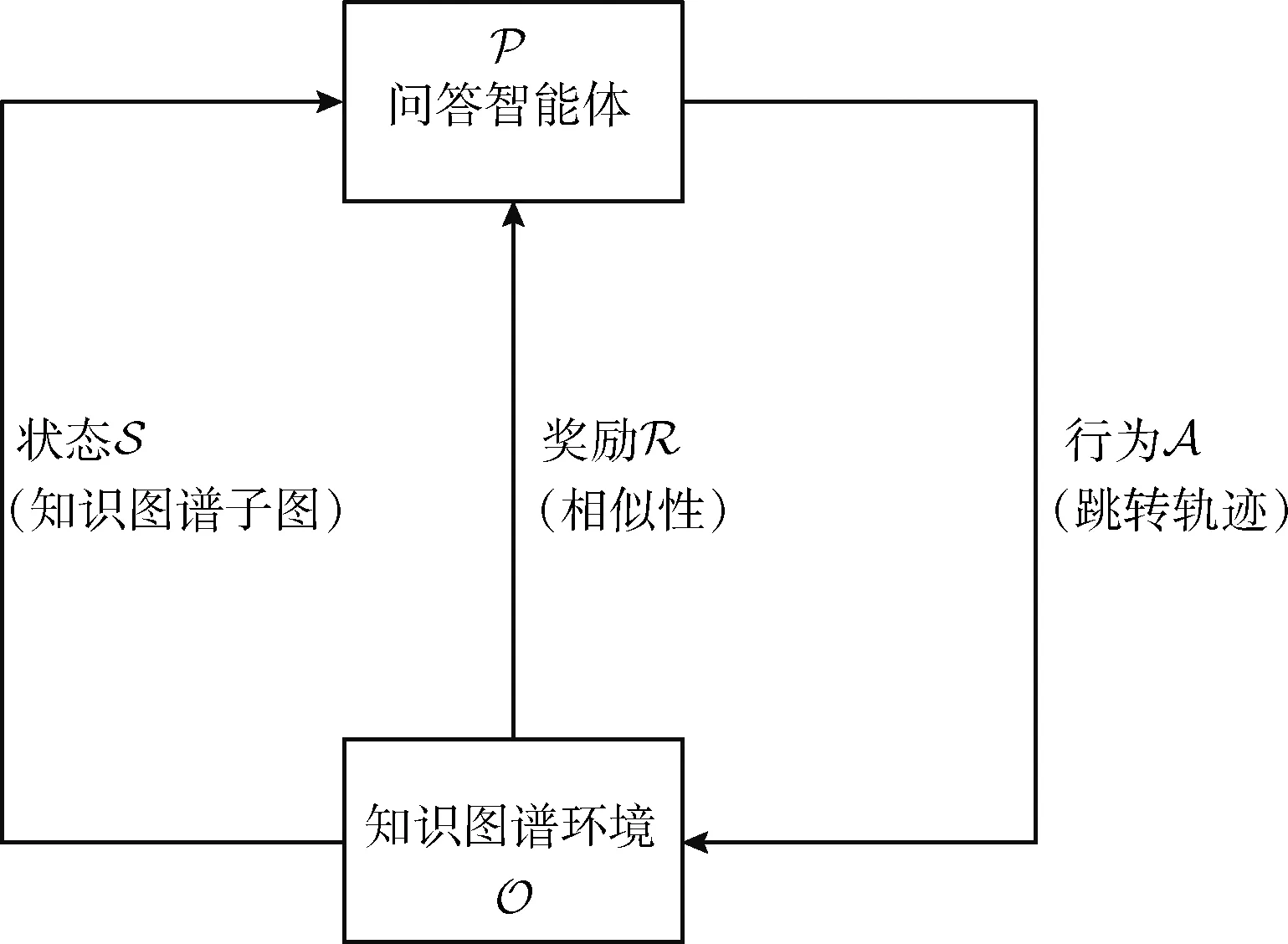
图2 知识图谱多跳推理强化学习架构

DRL-MHR采用策略梯度算法，建模强化学习框架只需考虑策略、环境和收益信号。

2.1 策 略

策略定义了学习智能体在特定时间的行为方式，是环境状态到动作的映射。在时刻t=(0，1，2，…)， 推理智能体和知识图谱发生交互：推理智能体获取观测Ot∈O， 策略选择动作At∈A， 作为对智能体动作的评价，智能体接收到一个数值化的收益Rt+1∈R⊂， 并继续获取新的观测Ot+1∈O。 以此类推，推理智能体和知识图谱环境共同得出一个交互轨迹：Ht=(O0，A0，O1，A1，…，Ot，At)。

参数化策略可以用更简单的函数近似，且能在系统中引入理想的策略形式的先验知识，因此本文采用策略梯度算法，直接学习参数化的策略，动作选择也不再依赖于策略的评估和改进，不会产生上文中的离散集合，下文使用记号θ表示策略张量形式的参数。

2.2 环 境

2.2.1 状态

状态空间S包含所有知识图谱节点信息的有效组合，推理智能体状态不仅包含时刻t所处的实体节点εt， 还包括时刻t0时所处的起始实体节点εμσ和关系边γσ， 以及最终答案节点ενσ。 因此可以定义时间步t时的状态St=(εt，εμσ，γσ，ενσ)∈S。 初始状态S0=(εμσ，εμσ，γσ，ενσ)， 终止状态ST=(ενσ，εμσ，γ，ενσ)。 状态更新是解决部门可观测性问题的核心部分，在获取新状态之前，推理智能体不能采取任何动作或者做出任何预测。

2.2.2 观测

推理智能体记录自身在时刻t所处的位置εt和输入的查询条件 (εμσ，γσ)， 因此可以设置观测函数Ot=O(St)=(εt，εμσ，γσ)。

2.2.3 动作

动作空间A是推理智能体处于状态St∈S时，知识图谱环境有效边信息的组合。在状态St下动作At被定义为

(1)

即在时刻t选择的下一步实体节点不在遍历过的历史节点列表中。推理智能体从查询条件σ的起始节点εμσ开始，通过策略网络预测最有可能的路径，不断探索直至达到目标答案实体节点ενσ。

2.2.4 状态转移函数

p(St+1，Rt+1|St，At)=

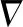
(2)

2.3 收益信号

在传统的知识图谱强化学习路径推理中，一般采用二元收益函数

R(St)=I{εt=εν}

(3)

即只有在当前实体节点是答案节点的时候才会获取的收益+1，否则其它时间步获得的收益都是0。这意味着推理智能体在不断地执行策略和策略评估后，最终只能得到很少的反馈，收益信号的延迟稀疏性不仅会导致强化学习延迟收敛，更有可能难以学习到有效的策略推理，笔者在知识图谱推理场景中采用收益塑造技术解决收益稀疏问题。

知识图谱Φ本质上是不完备的，二元收益方法对假阴性搜索结果的奖励与对真阴性搜索结果的奖励相同。为了缓解这个问题，使用模型表征相似性估算对正确性未知的目标实体的软奖励。在形式上，表征模型将节点集合Ε和边集合Γ映射到张量空间，通过余弦函数评估当前状态与下一步所选动作合并的事实三元组 (εt-1，γt-1，εt) 与知识图谱Φ中目标事实三元组 (εμ，γ，εν) 的相似性。函数f是后续章节3.3中介绍的表征网络，一方面余弦相似度可解释性强，计算简单；另一方面cos(x)∈[-1，1]， 其结果既可以是对正确路径的奖励，也可以是对错误探索路径的惩罚，得出下面的收益塑造函数

R(St)=I{εt=εν}+(1-I{εt=εν})cosf(εt-1，γt-1，εt)f(εμ，γ，εν)

(4)

如果εt是知识图谱Φ上解轨迹Ht的目标答案节点，推理智能体获得收益+1，如果εt不是知识图谱Φ上解轨迹Ht的目标答案节点，会根据当前事实三元组与真实三元组的余弦相似程度，被给予适量的奖励。

3 DRL-MHR模型

3.1 总体结构

基于深度图强化学习的知识图谱多跳推理架构如图3所示：图谱层、表征层和策略层。图谱层负责改造由事实三元组数据构建的知识图谱，在输入的知识图谱中添加逆关系和自环关系，方便下游的表征和推理任务；表征层接收图谱层生成的知识图谱，将知识图谱中的节点、边从语义和拓扑两个层面映射到统一的知识空间，便于策略层任务的矩阵计算；策略层包含一个深度强化学习结构，根据章节2.2中的建模要求组成知识图谱环境，推理智能体与知识图谱环境的不断交互中，探寻到与真实答案三元组在知识空间中最为相似的目标事实三元组。

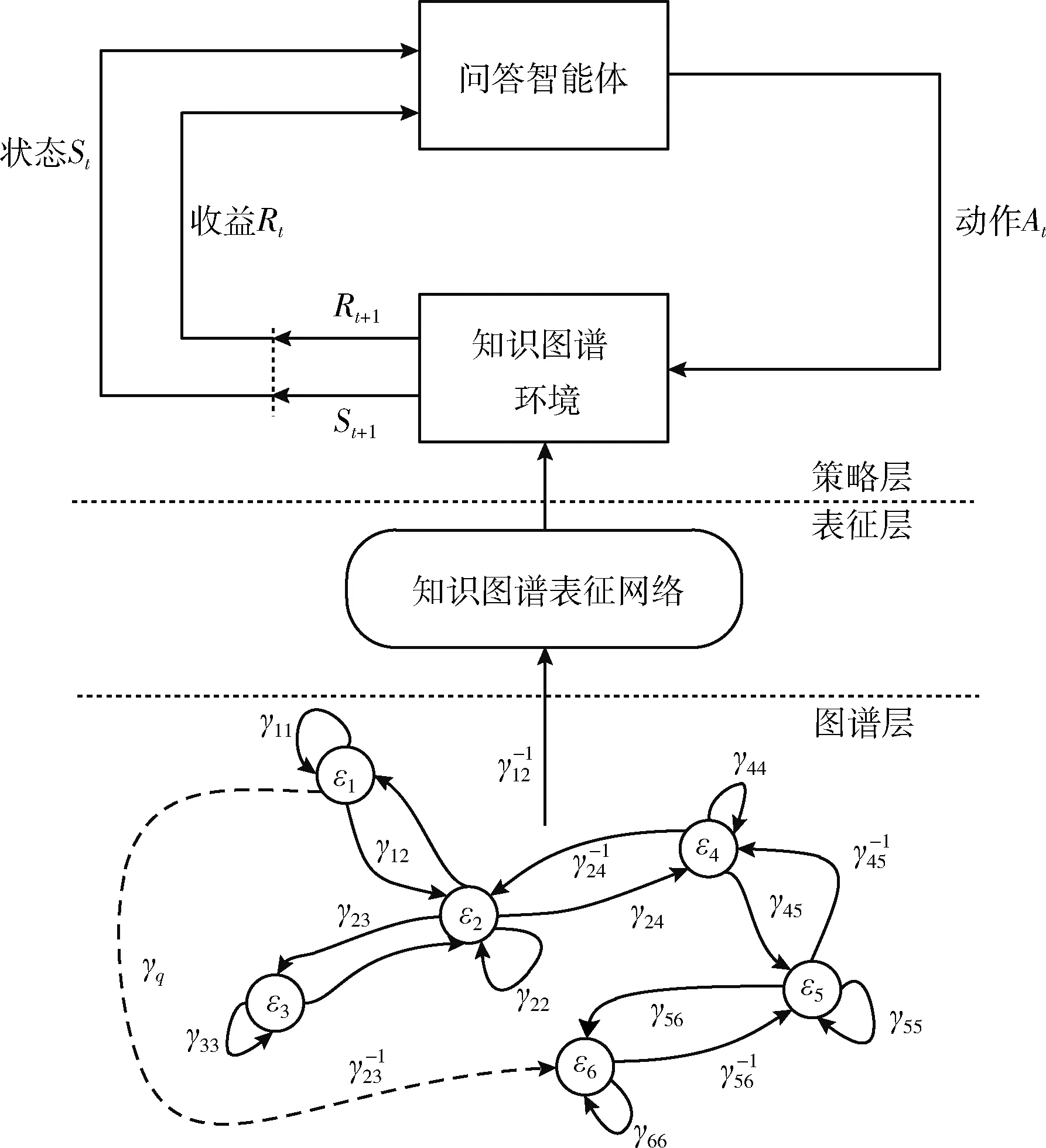
图3 DRL-MHR模型架构

3.2 图谱层

根据上述定义，知识图谱上的多跳推理被表述为：定义查询条件σ=(εμσ，γσ)， 求解输入为 (Φ，σ)， 解为历史轨迹Hσ=(εμσ，γμσ+1，…，ενσ-1，γνσ，ενσ) 的算法。

3.3 表征层

在知识图谱表征学习领域，ConvE[29]算法是一种被证明有效而且被广泛运用的算法，但是只有增加知识图谱中节点与边的拓扑信息，才能带来边际性能的增益。图网络学习中特有的“聚集-更新”机制无论在节点级别、边级别甚至图级别上的表征能力，弥补了ConvE未能充分利用知识图谱拓扑信息的短板，因此将知识图谱的网络表征分为语义表征和拓扑表征，这样最大限度利用了知识图谱提供的原始信息。

如图4所示，在表征层，知识图谱被分为节点索引和边索引的纯拓扑信息，以及带有节点和边信息的事实三元组两个部分。拓扑部分送入GCN训练，学习知识图谱中节点εi的拓扑表征εtopi=GCN(εi) 和边γj的拓扑表征γtopj=GCN(γj)； 事实三元组部分送入ConvE训练，学习知识图谱中节点εi的语义表征εsemi=ConvE(εi) 和边γj的语义表征γsemj=ConvE(γj)； 最终将拓扑表征张量和语义表征张量分别对应连接，得到节点εi的知识表征εi=[εsemi；εsemi] 和边γj的知识表征γj=[γtopj；γsemj]。

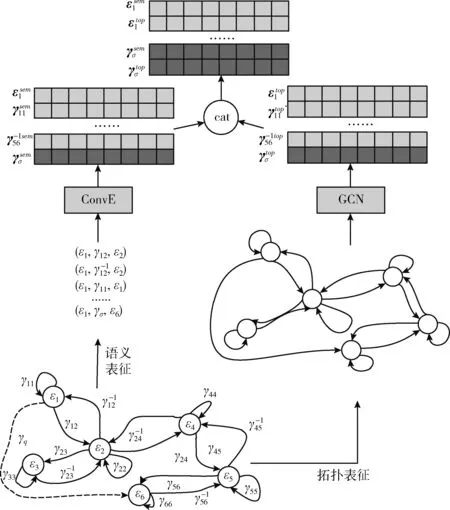
图4 DRL-MHR模型表征层网络结构

3.4 策略层

为了避免致命3要素，即同时使用函数逼近、自举法和离轨策略训练，防止出现策略不稳定和发散的风险。面对海量的状态空间和动作空间，只有利用深度神经网络强大的对策略非线性逼近能力和端到端的学习能力才能解决高维状态空间和动作空间的灾难，因此在知识图谱多跳推理非平稳环境中采用策略梯度算法。

图5右上角的张量列表是3.3节表征层中实体节点ε∈d和关系边γ∈d的嵌入表示，其中d为知识嵌入维度。为了构建知识图谱的强化学习环境，就需要按照2.2节的建模要求，构建强化学习的各个组件：待求解关系γσ=[γtopσ；γsemσ] 即为表征层中对该关系的拓扑和语义联合表征，动作At=(εt-1，γt，εt)∈3×2d即为知识表征后的实体节点和关系边连接组成的稠密张量，在问答智能体与知识图谱环境的多个时间步交互中，形成动作历史列表。观察Ot=(εt，εμσ，εσ)∈3×2d即为知识表征后的实体节点和关系边连接组成的稠密张量，在问答智能体与知识图谱环境的多个时间步交互中，形成观察历史列表。动作历史列表和观察历史列表按照章节的定义，组成了图5左上角的轨迹列表。图5的下部是问答智能体的深度学习网络，在得出下一步动作后，按照2.3节算法求解收益，本轮的收益被存入问答智能体的收益历史列表中，并将此次动作及动作后的观察分别记录到动作历史列表和观察历史列表中。至此完成一轮问答智能体与知识图谱强化环境的交互。

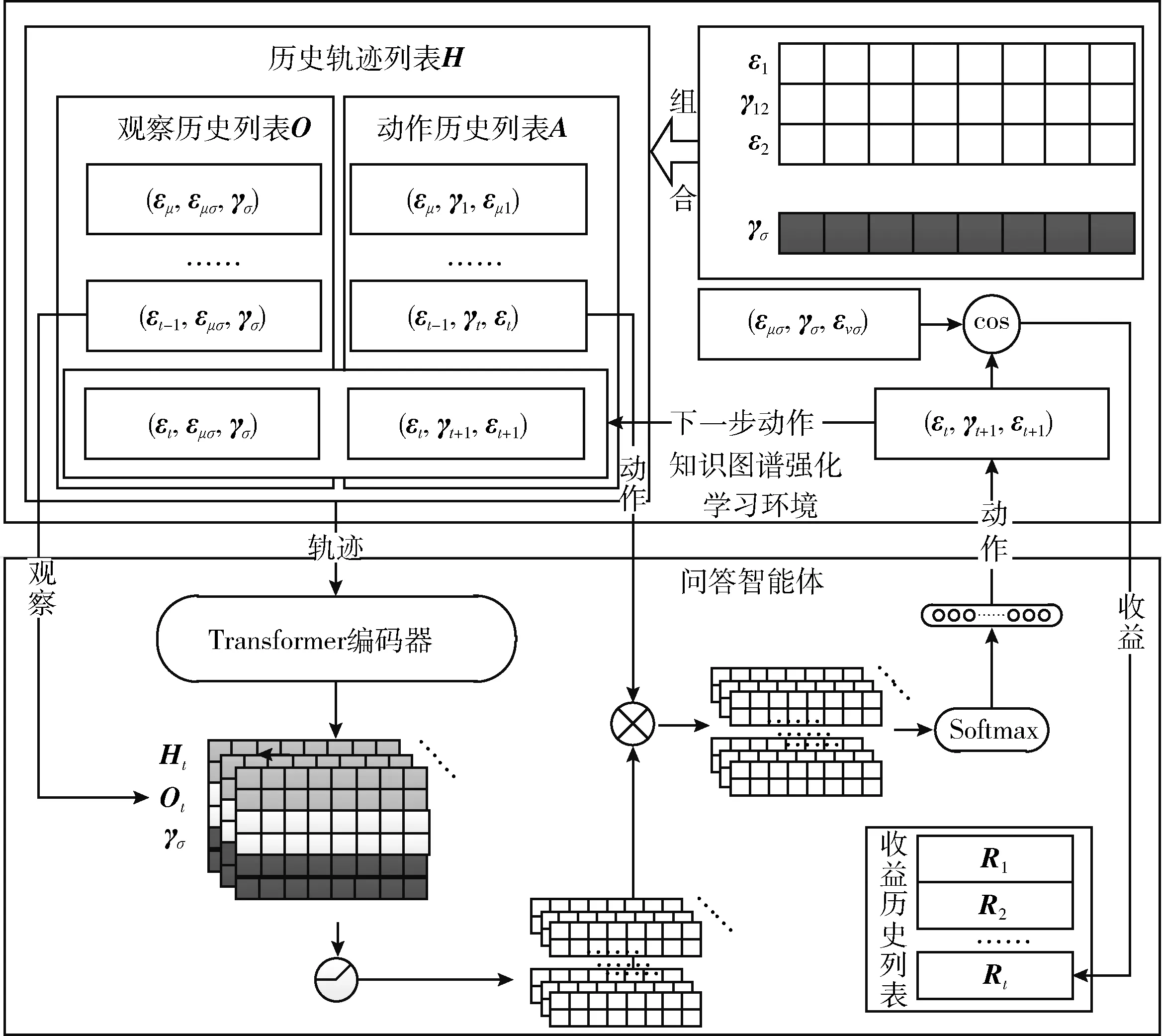
图5 DRL-MHR模型策略层网络结构

为解决有限视界确定性部分可观测马尔可夫决策过程，收益的概率随时间变化，历史轨迹列表H不再将观察历史列表和动作历史列表简单地组合，而是通过Transformer编码器将其编码为连续的张量H∈2d。 设计了一种随机非平稳历史相关策略π，并使用Transformer编码器参数化策略π=(π1，π2，…，πT-1)， 其中πtHt→p(A(St))，p为2.2.4节中定义的状态转移概率，时间步t的历史轨迹Ht=(Ht-1，At-1，Ot-1) 是关于曾经的观察和行动的序列。历史轨迹H通过堆叠3层Transformer编码器动态更新其张量表征。

如图6所示，首先将组成历史轨迹H的元素分别按照2.2节中介绍的方法，得到各自的拓扑表征和语义表征，将他们连接后得到最终的嵌入表征，将嵌入表征送入头多注意力，得到的注意力权重与嵌入表征做残差运算，经过层正则化后，降低数据方差，加快收敛速度，再经过一层前馈神经网络和层正则化，将结果送入下一个Transformer编码器，如此堆叠3次，得到最终的时间步t的历史轨迹Ht=Encoder(Ht-1，[At-1；Ot])，At-1表示在时间步t-1时的行为张量表征，Ot表示在时间步t时的观察张量表征，[；] 表示张量连结。关系的表征对应于智能体在时间步t时选择的边，实体的表征对应于智能体在时间步t时选择的节点。

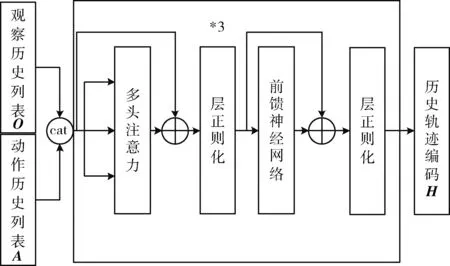
图6 推理智能体Transformer编码器网络结构

策略网络根据输入的查询信息，在知识图谱表征的强化学习环境中，从所有可用动作A(St) 中选择一个动作，每个可能的操作都表示一个包含关系边和目标实体的信息输出边。每一个动作表征可以被记为 [γl，εd]， 堆叠所有输出边的表征，得到矩阵Mt。 将其作为输入的网络参数化为具有ReLU非线性的两层前馈网络，该网络包含时间步t历史轨迹表征Ht、 观察表征ot和查询关系表征γσ的嵌入形式，从采样的离散动作中输出可能动作的概率分布。使用数学语言表述为

πt=softmax(Mt(W2ReLU(W1[Ht；ot；γt]+b1)+b2))

(5)

采用∈-贪婪算法获取动作结果

Mt={argmax(πt)a，(p=1-∈)random()，(p=∈)

(6)

知识图谱Φ是非欧几何空间，实体节点ε∈E没有固定的顺序，也没有固定数量的边γ∈Γ。 时间步t的动作空间矩阵Mt大小为2×|A(St)|×d， 此时的决策概率πt大小取决于 |A(St)|。 Transformer编码层参数、两层前馈网络权重W1、W2及其相应的偏差b1、b2构成了策略网络的参数。

3.5 训 练

策略梯度方法直接优化目标函数，并且在问题建立的时候就显式地表达出来。策略梯度方法使用神经网络的时候需要使用一些特殊的优化方法来解决一些问题。策略方法已经成为了很有竞争力的深度强化方法，主要得益于巨大的并行化潜力以及连续问题的解决能力。策略参数的学习方法都是基于某种性能指标J(θ) 的梯度，这些梯度是标量对策略参数的梯度。训练的目标是最大化性能指标，其更新近似于J的梯度上升θt+1=θt+αJ(θ)。J(θ) 的期望是性能指标对它的参数梯度的近似。在知识图谱多跳推理中，性能指标J(θ) 被定义为

J(θ)=(εμ，γ，εν)～D[(A1，…，AT-1)～πθ[R(ST)|S0=

(εμσ，εμσ，γσ，ενσ)]]

(7)

(εμ，γ，εν)～D是策略π下的同轨策略分布。为了解决这个优化问题，采用蒙特卡洛策略梯度算法REINFORCE。由分幕式问题策略梯度定理可知

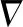
π[∑aπ(a|St，θ)qπ(St，a)π(a|St，θ)π(a|St，θ)]=

π[qπ(St，At)π(At|St，θ)π(At|St，θ)]

(8)

根据状态价值函数定义及2.2.4节中定义的状态转移函数可得目标函数梯度计算公式

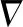
(9)

在训练的过程中，将累积收益的移动平均值作为基线，调整移动平均线的权重作为一个超参数。为了鼓励策略在训练时采样路径的多样性，增加了∈-贪婪算法中∈的数值、降低学习率等超参数，以更好维持探索与利用之间的平衡。

4 实 验

4.1 数据集

本文的实验选择常用的5种知识图谱数据集，涵盖体育、经济、政治等不同内容，容量从千级到十万级不等，尽可能测试出基于深度图强化学习算法的归纳偏置能力。表2中列出了UMLS[30]、KINSHIP[31]、WN18RR[32]、NELL-995[33]、FB15K-237[34]等5个数据集中关于实体、关系和事实三元组的数量统计信息。

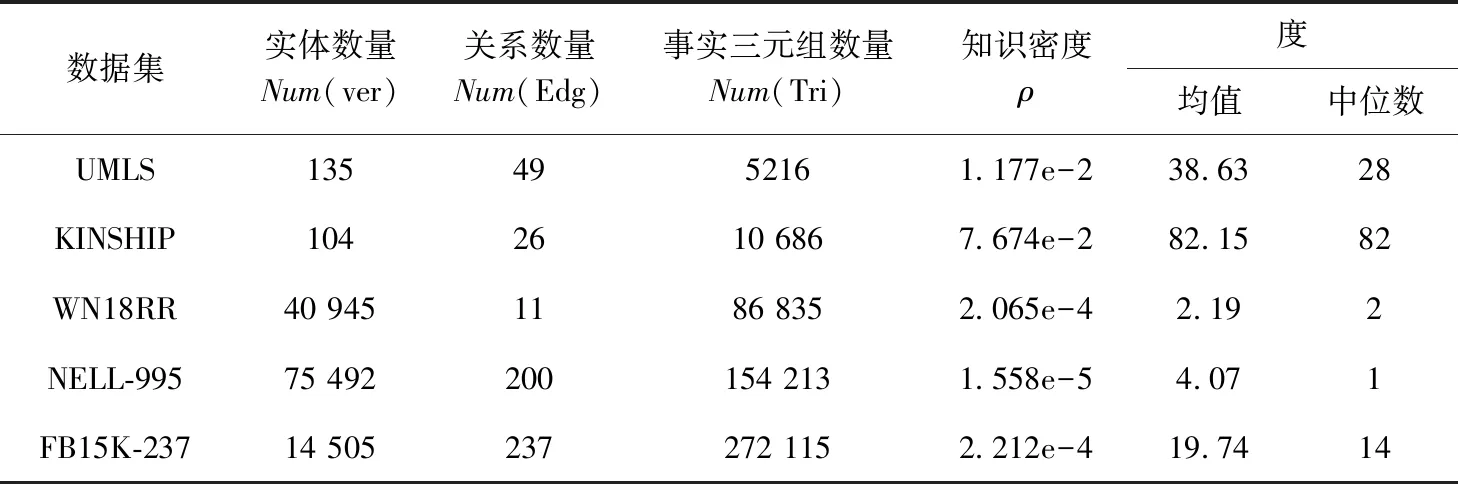
表2 数据集信息概要

其中知识密度计算公式为：ρ=Num(Tri)/(C2Num(Ver)×Num(Edg))， 意为数据集事实三元组与理想状态下全联通知识图谱事实三元组的比值，比值越高，表明知识越丰富，知识图谱越完善。从表2可以看出UMLS数据集和KIN-SHIP数据集的知识密度较高，事实三元组较为充分，WN18RR数据集、NELL-995数据集和FB15K-237数据集的知识密度极低，意即知识图谱中的事实三元组极为稀疏。

4.2 实验结果

作为对照实验，精选较有代表性的两类3种算法，基于知识图谱嵌入的ConvE、基于强化学习路径推理的MHKGR-RS及本文所述算法。ConvE算法将源实体和关系嵌入为张量，转换成矩阵后拼接，利用卷积核对拼接后的矩

4.2.1 命中率测试

Hits@n和平均倒数排名(mean reciprocal rank，MRR)是被用来评估多跳知识问答模型效果的指标。对于事实三元组K，Hits@n定义为[35]

Hits@n=1|K|∑|K|i=1I(ranki≤n)

(10)

|K| 为三元组集合个数，I(·) 是指示函数，即若条件真则函数值为1，否则为0，ranki指的是第个三元组的链接预测排名。

本文采用Hits@1和Hits@3度量指标，Hits@1是指正确答案是最终排序的第一个的占比，Hits@3是指正确答案是最终排序的第三个的占比。平均倒数排序MRR定义为

MRR=1|K|∑|K|i=11ranki

(11)

即是所有正确答案实体排名的倒数的均值。

从表3可以看出基于知识图谱嵌入方法在命中率上依然有着较强的优势，强化学习系列算法依然有着较大的进步空间。

表3 不同算法在数据集上命中率测试结果

4.2.2 累计收益测试

为了使测试结果更具有普适性，选择在UMLS、KINSHIP、WN18RR、NELL-995和FB15K-237等5个数据集上做算法效果测试，验证MHKGR-RS与DRL-MHR在累积收益方面的差异。(说明：图7、图8、图9、图10和图11中横坐标为智能体与环境的交互次数，纵坐标为智能体获得的累计收益。)

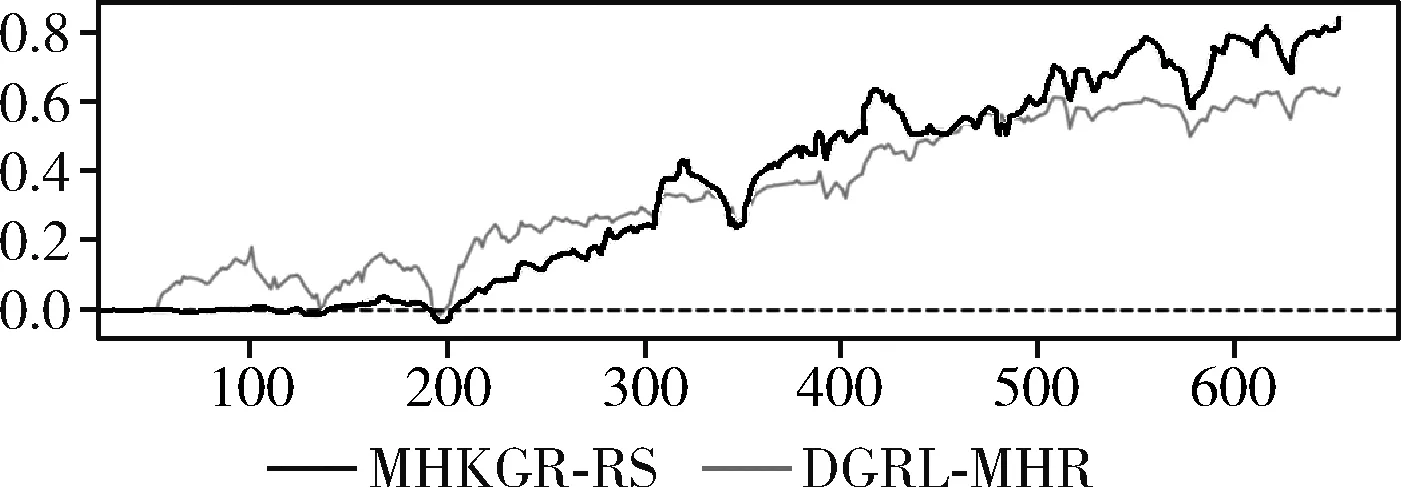
图7 MHKGR-RS与DRL-MHR在UMLS上的累积收益

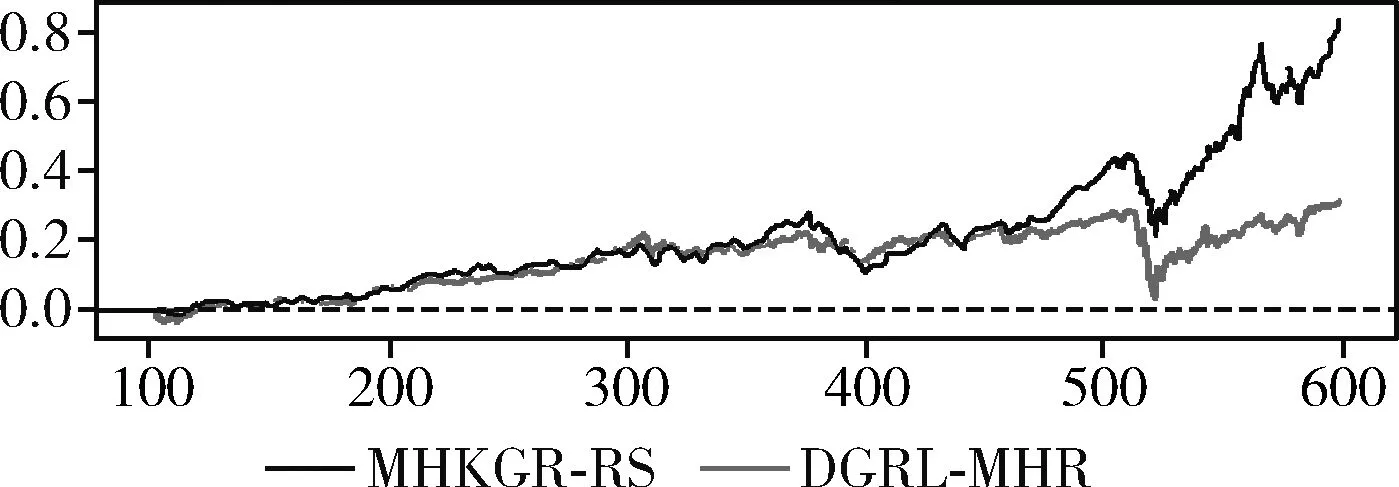
图8 MHKGR-RS与DRL-MHR在KINSHIP上的累积收益

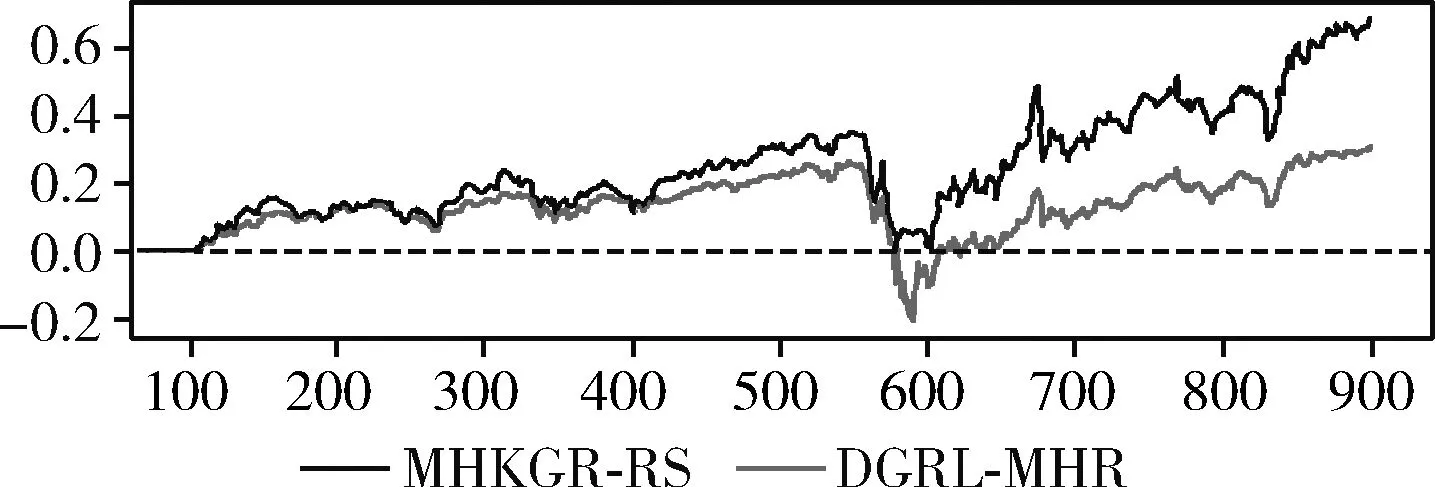
图9 MHKGR-RS与DRL-MHR在WN18RR上的累积收益

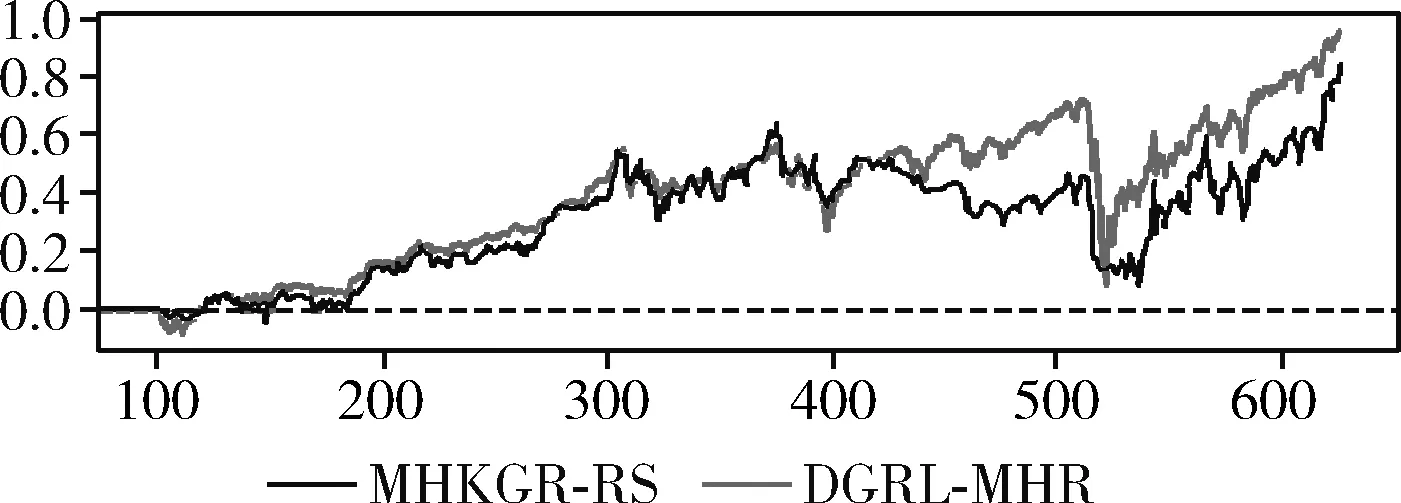
图10 MHKGR-RS与DRL-MHR在NELL-995上的累积收益

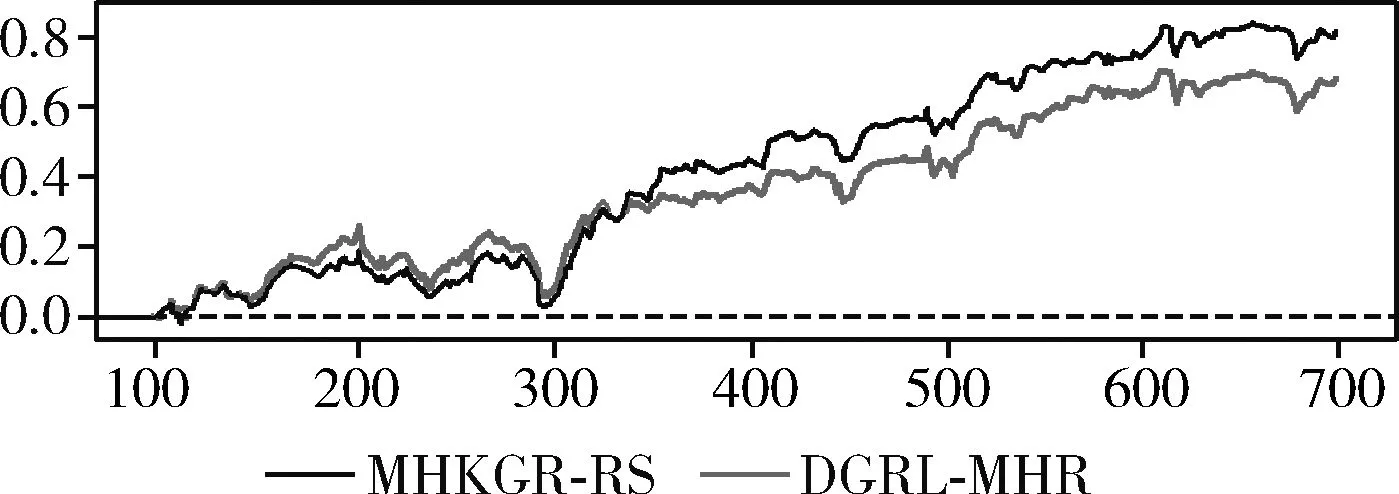
图11 MHKGR-RS与DRL-MHR在FB15K-237上的累积收益

4.3 实验分析

表3列出了ConvE、MHKGR-RS和DRL-MHR等多跳知识问答方法分别在UMLS、KINSHIP、WN18RR、NELL-995和FB15k-237等5个数据集上的实验结果，采用的评测指标有Hits@1、Hits@3和MRR。从表3可以看出：在UMLS和KINSHIP等小规模数据集上，3种算法效果并没有太大差异，甚至还在某些评价指标方面基于强化学习的MHKGR-RS和DRL-MHR不如基于嵌入的ConvE模型，这是因为这两个数据集事实三元组较为密集，关系路径较为完备，不会出现较多的缺失路径，以收益最大化为牵引的推理智能体并没有在路径搜索上体现优势，相反ConvE以其更加完备的语义表征能力，在包含稠密知识的数据集中效果更佳。DRL-MHR关注于找到实体对间的路径，并不会判断实体对是否为正样本，更适合处理一对多的关系类型。MHKGR-RS擅长应对带有噪声的推理场景，在稀疏的知识密度场景中具有更强的鲁棒性。在知识密度最为稀疏的NELL-995数据集中，DRL-MHR模型的表现弱于MHKGR-RS，Hits@1效果降低了17%。在知识密度较为稠密且接近的WN18RR和FB15k-237数据集上，DRL-MHR在Hits@1单项指标方面分别比MHKGR-RS高出了10% 和11%，这是因为MHKGR-RS智能体在训练时受到假负样本的影响，智能体可能被假搜索轨迹误导却偶然地被引向了正确答案，DRL-MHR采用收益塑造技术，高质量的奖励产生丰富的正确动作序列用于训练，使智能体探索更广泛的路径集合，以抵消对虚假路径的敏感度。

对于MHKGR-RS和DRL-MHR两种强化学习算法，如图8～图12所示，两种基于收益塑造的强化学习算法都具有明显的“冷启动”现象，甚至在某些节点的推理过程中会出现累积收益为负的情况，总体上DRL-MHR算法相较MHKGR-RS具有更高的累积收益，能够探索到更有价值的路径，获得更优的推理路径。但在NELL-995数据集上，MHKGR-RS算法的累计收益一直比同时间步的DRL-MHR高，这应该与NELL-995数据集中的数据有关，MHKGR-RS更擅长于处理一一映射关系，DRL-MHR算法不仅考虑到语义表征还综合了拓扑表征，相较随机游走和图线性自动编码器，对知识图谱拓扑信息做图卷积操作能够获得更加丰富的意含表征。DRL-MHR使用的收益塑造技术能够改善报酬稀疏问题。为了实现更有效的路径探索，使用价值函数对搜索目标进行评分，该价值函数根据历次累积的搜索历史进行更新。对于图10中MHKGR-RS在WN18RR数据集上累积收益为负的情况，分析WN18RR的度均值仅为2.19，而且知识图谱节点的出度、入度遵循幂等率，即节点的出度、入度数量变化极大，在均值极小，方差极大的场景中，智能体在有些节点上会有很大的动作空间，而在其它节点上动作空间又会很小，在动作空间很大的节点处做出错误决策的概率较高，这不仅影响策略梯度的收敛速度，甚至可能根本就无法收敛，是知识图谱多跳推理的难点问题，DRL-MHR的收益塑造算法改善了这一难点。

5 结束语

收益塑造技术能够缓解奖励稀疏问题，相较于基于符号逻辑规则方法通用性更好，相较于基于分布式嵌入方法可解释性更强，相较于之前的强化学习系列算法收益更平滑。将图神经网络与强化学习分别作用在算法的表征层和策略层，两者是上下游的关系，并没有直接发生关系。一种思路是凭借图神经网络提取任意图中局部连接特征的通用性及学习有效状态编码的适用性，利用逐渐增大的感受野产生的卷积层的潜在特征扩展智能体的搜索路径，使其能够有效扩充蒙特卡洛树搜索的“选择-扩展-模拟-回溯”流程。另一种思路是利用Transformer具备强大的语义表征能力和高容量序列建模能力，善于捕获超长视界的相关性，使用Transformer解码器对状态、动作、收益和回报等轨迹四元组进行自回归建模，生成下一步推理动作，将知识图谱多跳推理的序列决策问题转化成推理路径生成任务。当前信度通过计算自注意力得到新的信度估计值，满足长期信度分配的自举需求，取代基于模型的控制约束，建模轨迹三元组的分布，使用启发式集束搜索以最大收益为目标解码下一时间步推理轨迹。紧密融合图神经网络和强化学习将成为后续重点研究方向，为实现具有交互、感知、学习、反馈、进化能力的系统探索一条新的道路。