基于CS-MVDR的多目标方位估计新方法

刘 尚,蒋金华,段海洋,杜飞飞

(1.江南机电设计研究所,贵阳 550009;2.西北工业大学,西安 710072)

0 引 言

传统的多目标方位估计(Direction of Arrival,DOA)方法采用波束形成和最小方差无畸变响应(Minimum Variance Distortionless Response,MVDR)方法以及一系列如MUSIC和ESPRIT等高分辨率估计方法。这些方法利用均匀线性阵列进行多目标方位估计,难以解决因空时欠采样带来的阵元间相位差模糊的问题,部分信号方位角估计效果不理想。

压缩感知(Compressed Sensing,CS)理论是现代信息科学领域中一个全新的研究方向[1-2],对雷达信号处理、声纳成像[3]、模式识别、地质勘探、信道估计等都有重要意义,它提供了一种新的信号采集和参数估计方法,能够以远少于经典奈奎斯特(Nyquist)采样理论所需的测量数据精确恢复满足稀疏性的信号或估计其相应的参数[4]。信号在时域和空域的稀疏性特征满足信号稀疏重建理论的基本条件,利用随机采样矩阵可以实现用较低采样率的时域和空域数据恢复及估计信号的效果。相关学者从信号处理方法和阵元几何设计方面开展了研究:文献[5]提出基于时延、FFT和ESPRIT算法的高频段空间2D到达方向无模糊估计方法,但该方法估计信号数目受阵元数目限制;文献[6]基于窄带信号设计非均匀阵列,且阵元布放在均匀划分的以半波长为单位的网格点上,没有解决阵元间距小于半波长的问题;文献[7]提出利用CS理论对导向向量泰勒分解后,使用交替下降的最小二乘法实现信号重建,但此法利用混合范数的约束条件,重建过程中计算量较大,算法精度也受限。

为了解决上述空时欠采样条件下多目标DOA存在的问题,本文基于CS理论,采用空间网格角度划分形式实现信号在空间域的稀疏性表示,在此稀疏域下将实现信号与其空间位置的一一对应,对阵元接收信号在测量矩阵上进行压缩投影采样,通过改进MVDR空间功率谱估计中的压缩测量阵列接收信号的空间自相关矩阵和阵列流行向量的稀疏值,实现多目标方位角估计,最后通过仿真验证了本文方法的有效性。

1 多目标信号方位估计模型

信号方位估计是根据信号来波估计信号方位角的信号处理技术,是在空域滤波和空间谱估计基础上发展起来的[8]。空域滤波及空间谱估计理论框架如图1、图2所示。

用ωi表示加权系数,则相应的滤波器输出可表示为

(1)

图3给出了K个远场信号入射到某空间的均匀线列阵模型,其中阵元数为M。

图3 均匀线列阵模型

以均匀线列阵为例,阵列所接收信号的时延差为

(2)

两个阵元间的相位差为

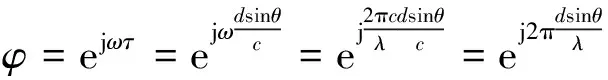
(3)

式中,d为两个阵元间距;c为信号在空气中的传播速度;θ为远场信号的入射角度;λ为信号波长。

可以看出,只要知道信号的相位延迟,就可以得到信号的来波方向,进而实现信号方位估计。

2 信号空域稀疏表示

均匀线列阵在某时刻t的接收信号的数学模型为

x(t)=As(t)+n(t)

(4)

式中,A为M×K维阵列流形矩阵,且

A=[a(θ1),a(θ2),a(θ3),…,a(θK)]

(5)

阵列流形向量为

(6)

式中,θi为第i个信号的入射方位角。

目标源的输入信号矢量为

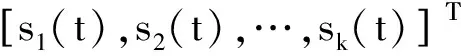
(7)

因此阵元接收信号可以表示为

=[a(θ1),a(θ2),a(θ3),…,a(θk)]S(t)+N(t)

=AS(t)+N(t)

(8)

由式(8)可知,阵列流行矩阵的每一列a(θi)都对应一个目标信号源的空间位置,即矩阵A包含了目标的方位信息。阵列流行矩阵的构建也决定了信号在空间域的稀疏化表示方式。

将空间域划分为{θ1,θ2,…,θNs},并假设每一个可能的位置θi,i=1,2,…,Ns都对应一个潜在的目标源信号si,如图4所示,其中“·”表示空间中实际存在的信号,○表示实际不存在的信号,矩阵A的每一列对应一个潜在目标信号源的方位信息。为了体现目标信号源的稀疏性,潜在的信号源个数比实际要多得多,即Ns≫K,这样就构造了一个Ns×N维的稀疏信号s=[s1,s2,…,sNs]Τ,N表示快拍数。在目标源信号s中只有实际存在目标的K个位置有非零元素,而Ns-K个位置均为零。

图4 信号空间稀疏化过程

对于给定的空间域稀疏化方式{θ1,θ2,…,θNs},式(5)中的阵列流行矩阵A得以确定,基于CS理论的DOA估计问题就转化为利用已知阵列接收数据x和阵列流行矩阵A来重构空间稀疏信号s=[s1,s2,…,sNs]T,该重构过程将一个凸优化问题转化为简单的线性规划问题来求解[9],其中前K个最大的重构分量就是空间上实际存在的信号源的重构信号。根据{θ1,θ2,…,θNs}与s=[s1,s2,…,sNs]Τ的一一对应关系就能得到信号的DOA估计。

3 CS-MVDR方法

MVDR[10]方法使一些自由度在期望观测方向形成波束,并利用剩余的自由度在干扰方向形成零陷,使非期望干扰最小,同时使增益在观察方向上保持为常数1,在减小非期望干扰的同时构建一个约束最优化问题:

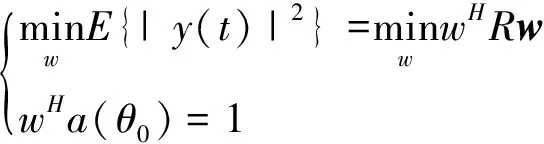
(9)

利用拉格朗日乘数法求解式(9),令目标函数

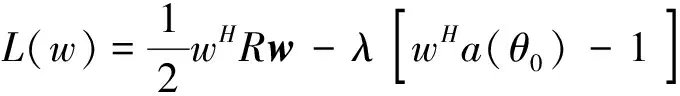
(10)

对目标函数中的w求导,令导函数为零,得到最优的权矢量为

w=λR-1a(θ0)

(11)

再利用wHa(θ0)=1可以求得常数

(12)

将式(12)代入式(11),得到最优的权矢量表达式为

(13)

阵列输出功率用空间谱描述为

(14)

根据压缩感知信号空域稀疏表示理论,阵列流行矩阵A相当于压缩感知理论中的稀疏矩阵Ψ,因此为了保证能够精确重构信号源,并得到方位角的准确估计,A必须满足一定的稀疏重构条件[11]。对于Ψ,当阵元数M小于稀疏系数矢量的长度Ns时,A相当于一个过完备基,即A是空域稀疏基。

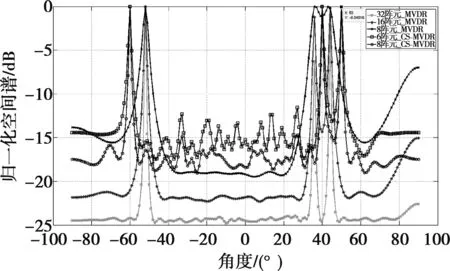
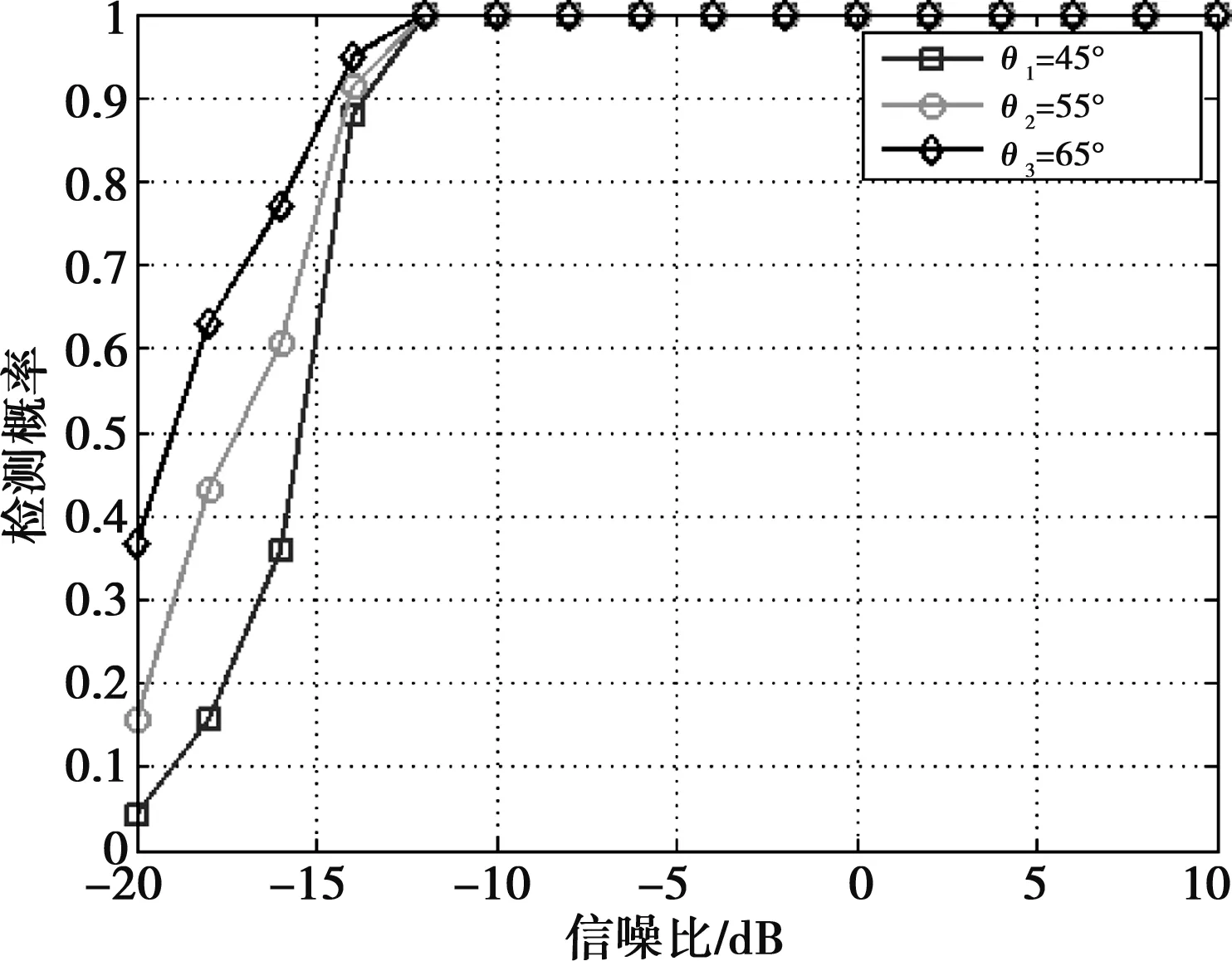
设Φ为m×M,m

由于随机稀疏测量矩阵满足RIP准则[12],因此利用压缩测量数据y和感知矩阵Θ即可大概率重构出阵列输入信号s=[s1,s2,…,sNs]Τ[13-14]。DOA估计问题就是求解Ns×N维的稀疏信号s,其中的非零元素及其在向量中的位置信息分别表征目标的幅度信息和角度信息,方位角估计就是在保证s在信号源真实方向相关的角度形成很明显的峰值,而在其他区域是近似为零的低电平,尖峰数量代表信号源数量。

因此,根据式(14),基于压缩感知改进的CS-MVDR阵列输出功率为

式中,b(θ)=Φa(θ)为压缩测量阵列流行向量;Ry为压缩测量阵列接收信号的空间自相关矩阵;a(θ)为传统阵列流行向量。

4 仿真及分析

对非均匀线列阵进行空时域欠采样,利用Matlab仿真比较MVDR和CS-MVDR在低信噪比、低阵元个数情况下的多目标方位角估计精度。

(1)仿真1:时域欠采样下的空间谱图

对传统阵列进行时域欠采样、空域正常采样。假设信号源个数为3,信号方位角分别为-60°、40°、50°,阵元间距选择半波长d=λ/2,采样频率选择小于3个信号源中心频率中最大频率的2倍(fs<2*fmax(1、2、3)),传统线列阵的阵元个数分别为8、16、32,压缩感知阵列阵元数为6、8,利用32阵列随机抽取得到。3个目标信号方位角的角度扫描范围为[-90°,90°],即在角度网格划分为N1=181。

图5、图6分别为信噪比0 dB、10 dB下利用压缩感知的6阵元和8阵元进行波达方向估计结果,采用随机稀疏测量矩阵,分别与8、16、32阵元下的MVDR估计结果作比较。

图5 时域欠采样下SNR=0 dB时的空间谱图

可以看出,8阵元MVDR估计在0 dB和10 dB下几乎都不能分辨临近的40°和50°目标,而6、8阵元CS-MVDR和16、32阵元MVDR均能正确估计出3个方位角度数。CS-MVDR方法在保证正确估计方位角精度的前提下减少了阵元数目,大大降低了计算量。相较于6阵元CS-MVDR,8阵元旁瓣起伏较小,方位估计稳健性更强。

(2)仿真2:空时欠采样下的空间谱图

对传统阵列进行时域、空域欠采样。信号源个数为3,信号方位角分别为-60°、40°、50°,阵元间距选择为半波长的1.2倍即d=1.2×λ/2,采样频率选择小于3个信号源中心频率中最大频率的2倍。信噪比为0 dB和10 dB时的仿真结果分别如图7、图8所示。

图7 空时欠采样下SNR=0 dB时的空间谱图

图8 空时欠采样下SNR=10 dB时的空间谱图

可以看出,8、16、32阵元MVDR估计在0 dB和10 dB下都不能正确估计3个目标方位角,而10 dB下基于压缩感知的6、8阵元阵列能正确估计出3个方位角度数,但是在0 dB下6阵元CS-MVDR法旁瓣起伏较大,甚至超过主瓣高度,8阵元的旁瓣起伏相对较小。

(3)仿真3:CS-MVDR法同时估计多个不同方位角

依然对3个目标信号源进行空时欠采样,信号方位角为45°、55°、65°。阵元间距选择为半波长的1.2倍即d=1.2×λ/2。信噪比从-20 dB步进到10 dB,步进长度为2 dB,快拍数为300,蒙特卡洛仿真次数为500,统计分析不同信噪比下多目标方位角估计的检测概率(当估计均值的绝对误差小于1°时,该次检测有效),结果如图9～11所示。

图9 信噪比与检测概率关系曲线

图10 信噪比与信号方位估计均值关系曲线

图11 信噪比与信号方位估计均方差关系曲线

可以看出,在低信噪比条件下,由于噪声对空时欠采样CS-MVDR算法的影响,检测概率相对较低,估计的信号方位角和真实值误差较大。不过,当SNR≥12 dB时,检测概率都能达到100%;当SNR≥-14 dB时,估值接近真实值,且估计的均方误差为零。在空时欠采样下,当同时估计多个信号方位角时,在误差收敛前不同角度间误差相差较大,这与目标入射角度来向和阵列流型矩阵A中对应的目标信号源方位信息有关,将在后续研究中进行深入分析。

5 结束语

针对传统MVDR方法在空域上采集测量数据量有限及对噪声背景相对敏感等问题,本文提出一种优化改进的CS-MVDR多目标估计方法,通过将空间角度网格划分形式实现信号在空时域的稀疏性表示,利用稀疏重构空间稀疏向量方法实现空间上多信号入射角的方位估计。仿真结果表明:在低信噪比条件下该方法对多目标方位估计精度更高,偏差更小,而且在不损失估计精度的前提下,可以在一定程度上减少雷达阵面的阵元数,降低复杂系统的运算量。

压缩感知理论为工程实践中信号稀疏化采样提供了一种新思路,把压缩感知理论运用到多目标方位估计中,可以解决部分工程应用中空时欠采样下的雷达目标回波探测和识别问题,不但降低了数据采用率、传输量、存储量,还减少了雷达阵面的总阵元数和T/R组件工程设计及结构减重等问题,同时提高了参数估计的准确性,克服了传统DOA估计算法的不足。