射流伺服阀前置级颗粒物空间分布数值研究

冯怡然，谢志刚，刘 莎，彭传龙，曹 伟，李奕宁

（航空工业西安飞行自动控制研究所，陕西 西安）

引言

射流伺服阀是液压系统中的核心元件，连接电液伺服系统的电气部分和液压部分，实现对信号的转换和对元件的控制。液压元件和流体介质在生产和使用过程中不可避免地会产生固体颗粒等污染物。这些颗粒跟随流体运动，可能会倾向性地停留或者聚集在特定区域，从而影响流体介质的流动状况及伺服阀的工作性能，严重时会造成设备失效甚至引发安全事故。伺服阀前置级的几何复杂性和流动的随机性以及固体颗粒的多样性，使得射流伺服阀前置级中颗粒- 流体两相流问题缺乏研究。本研究利用数值模拟方法，研究射流伺服器前置级流场中固体颗粒的行为。

1 射流管伺服阀工作原理

射流管伺服阀的主要组成可以分为力矩马达、射流管放大器以及滑阀等[1-3]，见图1。其中射流管伺服阀先导级为射流管放大器。射流管放大器由射流管和接收器组成，见图2。接收器上两接收孔分别与滑阀两端连接，当接收器内的流量达到饱和，油液从通道一侧回流至射流管的周围流场中。射流管喷嘴的偏移主要依靠衔铁组件控制。当无控制电信号输入时，衔铁组件保持在中立位置，两接收孔的压力一样，滑阀保持不动，无流量输出。当有控制电信号时，衔铁组件在力矩马达电磁力矩的作用下绕某一中心点偏转一定角度，两个接收器的流量变得不等，滑阀两端形成压差，在压差作用下驱动滑阀移动，反馈杆产生变形，当反馈力矩与力矩马达、弹惯性力矩等相平衡时达到稳定状态，伺服阀固定工作在某一平衡位置，输出与电信号成正比的控制流量。

图1 射流管二级力反馈式电液伺服阀结构原理

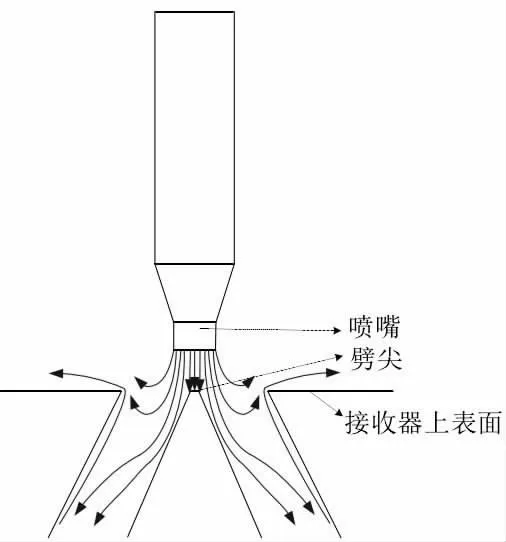
图2 射流伺服阀前置级流场结构示意

2 前置级流场计算模型

2.1 流动模型

伺服阀前置级流场计算模型见图3，喷嘴对中。全局的最大网格尺度设置为0.4 mm，为保证计算精确度，喷嘴附近网格进行局部加密。最终网格数量为1 837 230，网格质量均在0.3 以上。本研究采用FLUENT 软件计算，选择基于雷诺方程的RANS 模型，湍流模式为k-omega-SST 两方程模型，用SIMPLEC方法进行压力- 速度的耦合。整个求解过程使用瞬态计算。时间推进格式为一阶隐式离散格式。

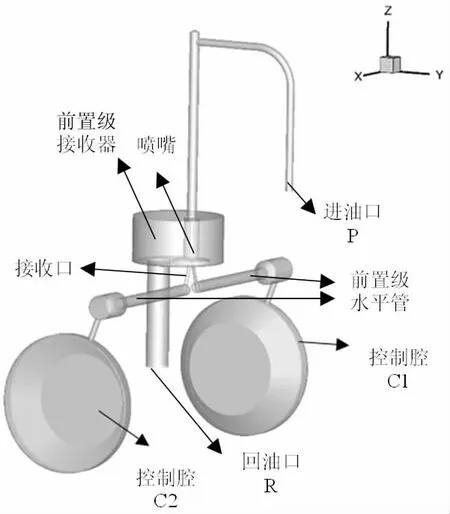
图3 伺服阀前置级流场计算模型

2.1.1 流体流动控制方程

流体介质的流动采用不可压缩的无滑移边界条件的Navier-Stokes（NS）方程来描述[4-6]，忽略流动传热和重力影响。基于连续性方程和动量方程可得雷诺平均运动方程：

式中：xi为Cartesian 坐标系3 个坐标方向；Ui为雷诺平均后的流体在i 方向上的速度分量；P 为压力；uiuj为雷诺应力。

2.1.2 颗粒相模拟

颗粒相使用的欧拉- 拉格朗日耦合方法DPM模块。除进口和出口使用逃逸条件之外，其他所有边界均为反射条件[7]。颗粒形状为球形，粒径分别为R=1、5、15、25、50、100、200 μm，材料为钢。因此固体颗粒的平动运动的动力学方程为：

忽略球形颗粒的转动。式中：up为颗粒速度；uf为流体的动力黏度；ρp为颗粒密度；Dp为微粒粒径；Rep为基于微粒直径的颗粒雷诺数。

式中：uf@p为颗粒位置流体的速度。

2.2 边界条件

如图3，进油口（P）和回油口（R）分别为压力入口和压力出口边界条件，具体设置见表1，入口施加5%的湍流脉动。其余边界设置为无滑移壁面。

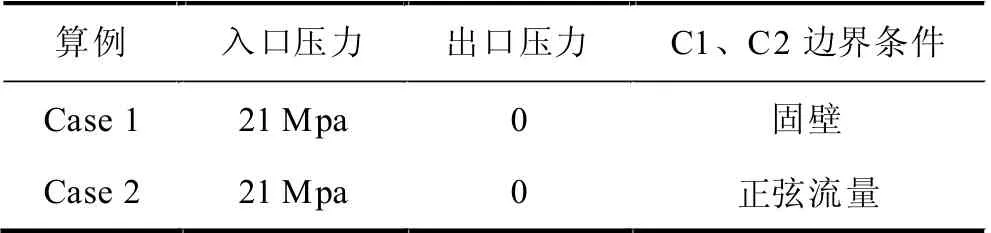
表1 伺服阀前置级流场中颗粒行为研究算例设置

3 颗粒空间与速度分布

在本研究中，流场颗粒两相流计算方法如下：首先进行流场稳态计算直至收敛，接着已收敛的稳态流场的基础上进行瞬态流场计算1 000 步，再加入颗粒瞬态计算20 000 步，最后输出颗粒场。在这20 000步的计算中，前500 步在入口处以surface 类型释放前述7 种不同粒径的球形颗粒。总共向流场中加入227 500 颗粒，其中每种粒径的颗粒数均为32 500。

3.1 零位工作状态模拟

本节研究了伺服阀的零位工作状态时的前置级颗粒运动和速度分布，当C1、C2 为固定壁面时的伺服阀前置级颗粒运动和速度分布情况。

图4 展示不同直径颗粒的空间分布图（左）和归一化的颗粒速度分布直方图（右）。从颗粒空间分布图可看出，颗粒相的空间位置分布受颗粒尺寸影响较为明显。整体而言，颗粒主要分布在前置级接收器、前置级水平管、回油管区域。如图4 所示，对于小颗粒（R≤15μm），少量驻留在进油管的顶部，由于弯管处流场出现旋涡，小惯性颗粒被旋涡产生的离心力作用甩到顶部位置，因此长期驻留于此；多数则集中在靠近喷嘴一侧的水平管中，这是由于小尺寸颗粒的惯性小，无法到达远离喷嘴的水平管区域[8]。随着颗粒尺寸增加，惯性增加，颗粒不再驻留在进油管顶部，而水平管内的颗粒分布更为接近左右控制腔体。

图4 颗粒的空间分布图和速度分布直方图（固壁面）

本算例中，C1、C2 端面为固壁边界，因此水平管和控制腔内的流体几乎不流动。小惯性颗粒在喷嘴处获得的高速动能在进入接收口后逐渐衰减，因此难以运动到控制腔[9]；而大惯性颗粒则会较缓慢地损失动能，因而可以在水平管内运动较远距离，甚至到达控制腔。从速度分布图可知，颗粒越大，颗粒速度大小越集中在0，与颗粒空间分布图中颗粒颜色分布一致。这说明经过一段时间的发展，大尺寸的颗粒更倾向于停留在低速的流体区域。

为了进一步分析不同粒径颗粒在伺服阀中能否随着流体被带出，本研究定义了颗粒整体停留率γ和局部停留率ψ：

式中：n1是停留在接收口以下区域的颗粒数；N 为加入流场的总颗粒数，n 为停留在伺服阀内的颗粒数。

由图5 可知，整体停留率γ 随着粒径的增大而增加，1μm 的颗粒具有最小的γ=22.49%，15μm 的颗粒具有最大的γ=82.10%，随后γ 随粒径增加略有减小，但变化幅度较小。局部停留率ψ 呈现出与γ基本一致的变化趋势。直径大于及等于15μm 的颗粒的局ψ 值均大于63%。以上结果说明，若颗粒不能跟随流体从出口流出，则会有较大的概率停留在前置级内。

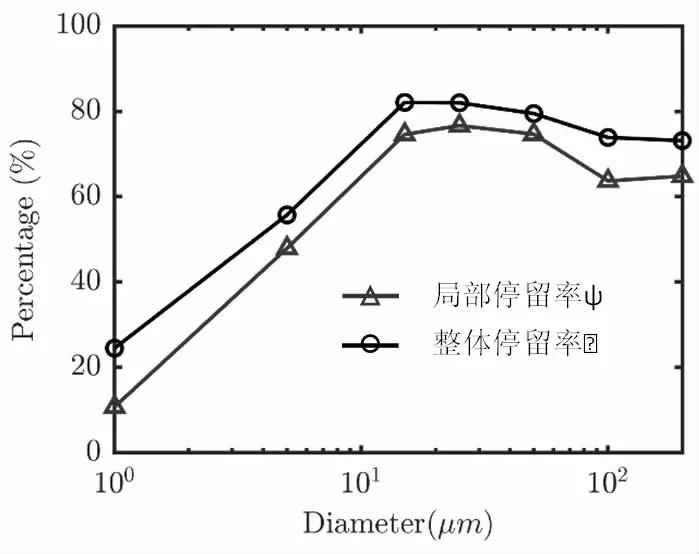
图5 前置级整体停留率和局部停留率随粒径的变化规律

3.2 正常工作状态模拟

本算例中，C1、C2 端面的边界条件为速度入口，该速度为正弦体积流率对应的端面移动速度，且C1、C2 端面的流量的正负号相反（见图6）。本算例定义流体向阀体内流入时流量为正，否则为负。本算例对应正常工作状态/磨合工作状态的伺服阀。

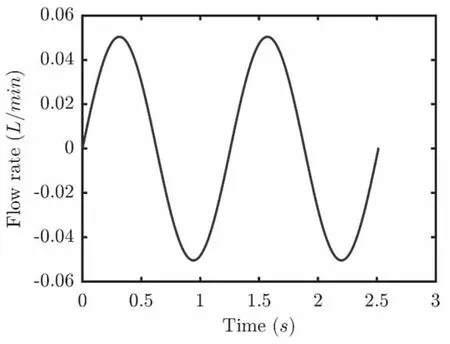
图6 C1 端面体积流率随时间变化曲线

图7 展示了从入口处加入颗粒约1.25 s 后，不同粒径颗粒的空间分布和速度分布。由于此时C1 流体流入C2 口流体流出，颗粒大部分会随流体带动进入C2 侧的水平管和控制腔体，接收器中颗粒减少，且颗粒速度非常集中，在0 附近。

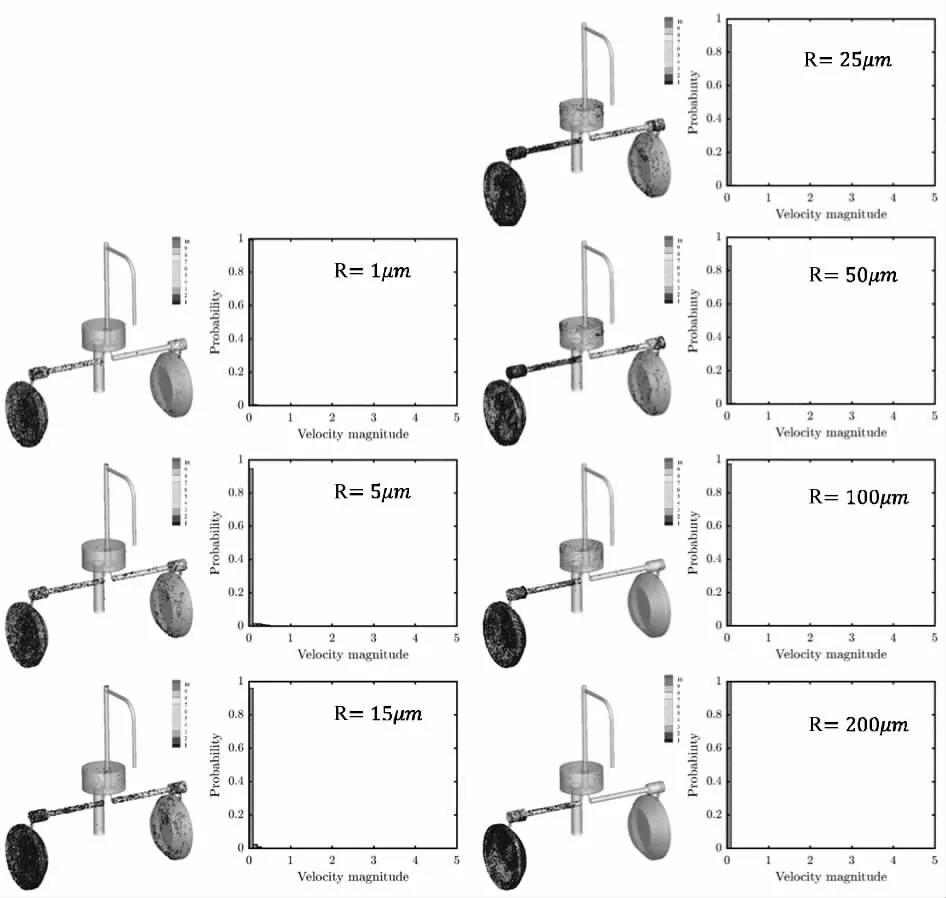
图7 颗粒的空间分布图和速度分布直方图（正弦流率壁面）

由图8 可知，相比于C1、C2 口为固壁的情况（见图5），本算例中颗粒的整体停留率γ 和局部停留率ψ均显著减小，且γ 和ψ 值更加接近，说明阀体内的颗粒更容易随着液流被带出前置级，从而使得阀体内的颗粒更少。

图8 前置级整体停留率和局部停留率随粒径的变化规律

为了进一步探究颗粒停留率随时间的变化关系，对图8 所示的计算结果续算了125 664 步（对应的时间为正弦函数的一个周期）。图9 展示了从入口处加入颗粒约1.25 s（虚线）和2.51 s（实线）后颗粒的整体停留率γ 和局部停留率ψ。由图可知，随着时间的增加，无论颗粒的尺寸大小，颗粒的整体和局部停留率均有一定幅度的降低。可以看出，随着计算时间的延长，伺服阀前置级的颗粒停留率可以被有效降低。

图9 不同时间下前置级整体停留率和局部停留率随粒径的变化规律

4 结论

本研究通过数值模拟手段研究了射流伺服阀前置级内的流体- 颗粒两相流问题。针对伺服阀的两种不同工作状态，重点研究了单向耦合中不同尺寸的固体颗粒在流场中的运动学行为和空间分布。具体结论如下：

（1）颗粒会在伺服阀前置级中展现出倾向性的聚集行为，且长时间驻留在伺服阀内（特别是接收口及以下区域）。

（2）控制腔C1、C2 端面边界条件为正弦流率相比其为固定壁面时，颗粒相的停留率更低。

（3）控制腔C1、C2 端面边界条件为正弦流率，随着磨合时间的延长，伺服阀前置级内颗粒停留率展现出降低的趋势。