隧道火灾不同CFD 模型的对比分析及试验验证

高才驰 ,陈宁威 ,陈 飞 ,张小宁

(1.苏交科集团股份有限公司,南京 210019;2.南京地铁运营有限责任公司,南京 210008;3.山东大学土建与水利学院,济南 250061)

随着交通网络的不断完善,我国隧道的数量也在逐年增加[1]。据中华人民共和国交通运输部发布的《2021 年交通运输行业发展统计公报》,截至2021 年年底,我国已有公路隧道23 268 处,总长2 469.89 万延米。隧道在方便人们出行、提高运输效率的同时,也伴随着火灾安全隐患。虽然隧道火灾事故发生的频率不高,但是一旦发生,造成的损失往往十分重大[2-5]。2017 年,山东省威海市陶家夼隧道火灾造成13 人死亡,其中11 名是儿童;同年,河北省保定市浮图峪隧道发生火灾爆炸事故,造成15 人死亡,直接经济损失逾4 200 万元。近年来,新建的隧道结构更加复杂[6-11],传统的隧道火灾烟气控制方案可能失效,给隧道消防安全带来了新挑战。在获取隧道火灾数据时,试验虽最可信[12],但是存在成本高、周期长、数据少等缺点;而理论分析基本无法给出隧道内物理场的解析解。数值模拟能够给出隧道火灾发生、发展、熄灭全过程的信息[13-15],并合理预测温度场和烟气流动的特征[16-17],具有成本低、数据丰富等优点。在隧道火灾的数值模拟方面,CFD 模拟是应用最广泛的方法[18],其代表软件有FDS(Fire Dynamics Simulator,火灾动力学模拟工具)、FLUENT 和PHONIECS。借助这些软件,学者们对诸多隧道火灾场景开展了数值模拟研究。在顶棚下方最大温度方面,Hu 等[19]通过FDS 模拟与全尺寸试验的对比,验证了Kurioka 模型的准确性;姚坚[20]使用FLUENT 软件模拟了不同纵向风速下的温度场变化规律,建立了描述隧道火灾纵向和横向温度的近似公式。陈长坤等[21-22]使用FDS 软件研究了火源面积对隧道内温度分布的影响。在烟气运动方面,Wang 等[23-24]使用FLUENT 软件模拟了弯曲隧道发生火灾时的临界风速。Yang 等[25]模拟了隧道内发生火灾时的烟气流动。FLUENT 软件是常用于火灾模拟计算的软件,但使用FLUENT 软件计算得到的隧道火灾温度一般都偏高[20],因此有必要对FLUENT 软件支持的多种CFD 模型进行对比分析,提出结果准确、计算成本低的模型,为研究隧道内火灾的数值模拟提供参考。

湍流模型和燃烧模型是计算隧道火灾的两个重要工具,受到了众多学者的关注。Gao 等[26]对比了LES((Large Eddy Simulation,大涡模拟)和标准k-ε方程,认为LES 能够更好地模拟烟气回流和隧道断面的热分层现象,但是两者均高估了隧道内的烟气温度。Maele 等[27]对比了LES 和RANS(Reynolds-averaged Navier-Strokes equations,雷诺平均方程)模拟的通风良好的水平隧道发生火灾时的临界风速,发现RANS 给出的预测值偏小而LES 偏大。Yang 等[28]和 Xue等[29]对比了体积热源(volumetric heat source,VHS)模型、涡旋破碎(eddy break up,EBU)模型和概率密度(probability density function,PDF)模型,发现不同燃烧模型对室内火灾的预测结果缺乏良好的一致性。

以往的研究使用FLUENT 软件进行隧道火灾数值模拟时,采用的燃烧模型(如体积热源法、组分PDF 模型等)和湍流模型(如RANS 或LES)不尽相同,甚至物理模型也不相同,如是否扩大计算域、是否考虑壁厚等。Mcgrattan[30]指出,对于一个特定火灾场景,不同的CFD 模型没有对与错,只有合适与否。鉴于此,本文选取单管直隧道火灾场景,首先利用搭建的缩尺试验台开展试验,然后使用FLUENT 软件,通过对比不同物理模型、燃烧模型和湍流模型的计算值与试验值的差异,筛选出适用于隧道火灾模拟的CFD 模型,为复杂结构隧道火灾模拟提供参考。

1 缩尺试验设计

搭建模型开展试验,1 ∶6 缩尺寸分岔隧道模型示意如图1 所示。主隧道长20.0 m,宽1.2 m,高0.9 m,横截面为矩形,火源位于主隧道中央。隧道骨架由3 mm 厚的钢板制成,内表面使用5 cm厚的石棉板保护。将石棉板表面处理平整,以尽可能减小壁面摩擦阻力。使用热电偶树测量隧道内纵截面上的温度分布,热电偶布置如图1(a)所示。其中,最高的热电偶位于顶棚下方9 cm 处,用以测量顶棚下方的最大温度。距离火源1 m 的范围内,热电偶树的间距为0.25 m;这个范围以外,热电偶树的间距为0.5 m。在距离一端口1 m 处安装一台摄像机,记录火焰形态。使用边长为0.4 m 的方形乙醇池火模拟火源,乙醇纯度为99%。用电子天平记录乙醇的质量损失速率,电子天平精度为1.0 g。热释放速率通过质量损失率计算,燃烧效率取1.0。点火前燃料厚度保持在10 cm。环境温度约为10 ℃。

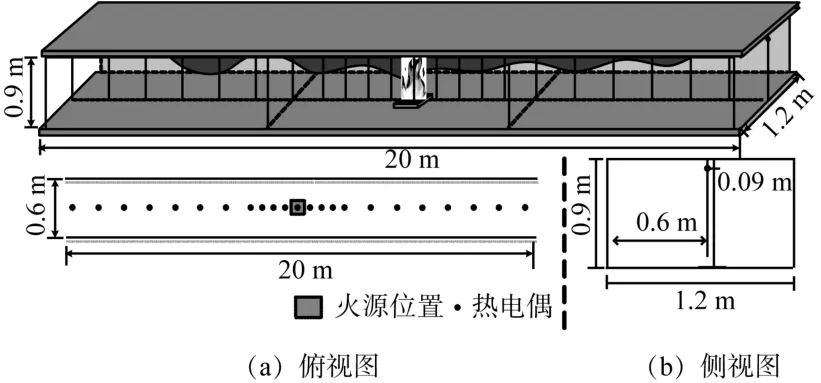
图1 1 ∶6 缩尺寸分岔隧道模型示意

2 数值模拟模型及设置

2.1 物理模型

按照缩尺寸试验装置建立3 种不同的物理模型。第1 种物理模型与缩尺试验台相同,但没有体现壁厚;第2 种物理模型在隧道两端口增加两个六面体,以消除隧道出口边界条件对隧道内流场的影响;第3 种物理模型在第2 种物理模型的基础上体现了壁厚,使流体能够向隧道壁面散热。后两种物理模型的具体尺寸如图2 所示。

图2 后两种物理模型的具体尺寸

2.2 燃烧模型

隧道火灾模拟常用的燃烧模型有体积热源法和燃烧速率计算法。体积热源法不计算化学反应速率,直接将火源简化为一个发热体,即对空间内位于火焰内部的网格添加能量源项,其值等于火源功率,计算方法为

式中,cell 表示网格单元,[flame region] 表示火焰区。

体积热源法虽不能考虑火焰形态,模拟的烟气生成量也比实际小,但是计算量不大,能给出较合理的临界风速预测值,因此被很多学者采用[24-25,31-32]。

由于VHS 模型仅考虑了火源对计算域热量的传递,没有考虑热烟气的生成,因此基于Heskestad羽流模型,提出传质体积热源(mass transfer-volumetric heating source,MT-VHS)模型,该模型能够在VHS 模型的基础上释放热空气以模拟火羽流。Heskestad 模型认为火源热烟气的质量流量可以描述为

综合式(1)～式(3)可得MT-VHS 模型的表达式。可以看出,在质量传递方面,该模型能够将符合实际量的热烟气送入计算域;在热量传递方面,该模型继承了体积热源法的优点,能够产生稳定功率的热量,但该模型没有考虑空气卷吸。气体描述模型决定了气体的流动传热状态,主要参数包括密度、定压比热、导热系数和动力黏度。为了减少模拟计算量,本文认为热烟气是温度高的空气。空气的物性参数使用拟合的曲线来表示[32]。

火灾数值模拟中,常用的湍流模型有k-ε双方程模型和大涡模拟。k-ε双方程模型是雷诺平均方程中的一种,它采取了工程上可接受的、将温度等物理量进行时间平均的处理方式,因而极大地减少了计算量;而大涡模拟基于涡旋的能量级串原则,不对物理量进行时间平均,直接对涡旋进行模拟计算。以往学者在进行火灾模拟计算时,两种湍流模型均被使用。下文将对比两种模型的计算结果。

2.3 模拟工况设置

空气的流动和热物性参数对火灾时的温度等有直接的影响。常用的布辛涅斯克近似理论仅能适用于温度变化不大的场景(如自然对流等)。因此,本文通过对空气在300～2 000 K 之间进行拟合,使用得到的拟合公式来描述空气在不同情况下的流动和热物性。空气物性参数随温度的变化如表1 所示。

表1 空气物性参数随温度的变化

为对比不同物理模型、燃烧模型、气体描述模型和湍流模型的特点,筛选出合理的模型,模拟工况设置如表2 所示。使用ICEM 软件划分结构化网格,并对火源附近的网格进行加密。网格独立性验证表明,使用总数为56 万的网格能够兼顾准确性和经济性。试验中质量损失速率为1.32 g·s-1,折合火源功率为35.34 kW。因此在使用VHS 模型时设定=35.34 kW。试验中使用的乙醇燃烧时产生的热烟气量很少,总的热释放中以热辐射的形式散失的热量占比较小,因此取

表2 模拟工况设置

3 结果及分析

3.1 顶棚下方的纵向温度分布

VHS 模型中不同设置的顶棚下方温度分布预测值与试验值对比如图3 所示。

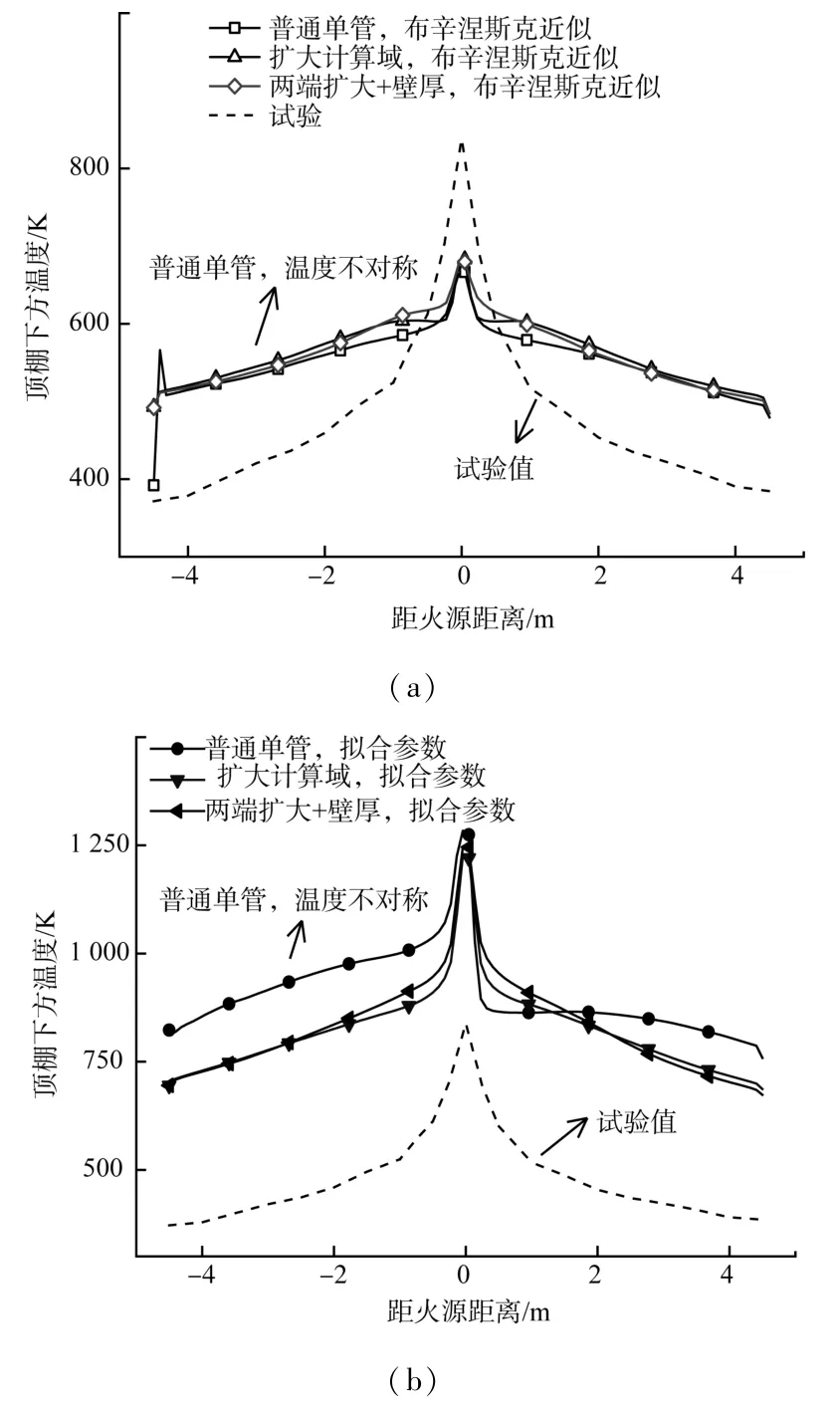
图3 VHS 模型中不同设置的顶棚下方温度分布预测值与试验值对比

图3(a)为使用VHS 模型(即工况A1～A6)300 s 时顶棚下方的纵向温度分布。可以看出,使用布辛涅斯克近似计算的顶棚下方温度比使用拟合参数计算的低200～500 K。布辛涅斯克近似认为空气物性是常数,而随着温度升高,空气密度降低,导热系数增大,比热基本不变,因此空气的热扩散系数α=λ/ρc随着温度升高而增大,使空气温度剧烈升高。VHS 模型不能对顶棚下方温度给出准确的预测值。此外,由图3(b)可以看出,若模型没有扩大计算域,温度分布可能是严重不对称的,这可能是隧道出口边界条件设置的影响。实际的隧道出口存在中性面[34],压强必定有变化。若不考虑扩大计算域,则在设置边界条件时,隧道端口被认为是等压强的。是否考虑壁厚对温度影响不大,因此在工况B 组中仅使用扩大计算域的物理模型。

MT-VHS 模型顶棚下方纵向温度分布与试验值的对比如图4 所示。由图4 可以看出,当设定气体性质为拟合参数时,该模型对火源近场的温度预测效果非常好,但是对火源远场的预测效果较差。现实中,烟气通过卷吸空气和向壁面散热降温,而在模拟中没有考虑壁面的对流散热。同时,模拟火源没有卷吸周围的空气,热烟气与冷空气之间的剪切流动不强,这两个原因导致火源远场的温度较高。其他设置相同时,LES 给出的顶棚下方纵向温度曲线波动较标准k-ε方程的大,原因可能是LES 没有进行时间平均。

图4 MT-VHS 模型顶棚下方纵向温度分布与试验值的对比

3.2 顶棚下方最大温度

使用布辛涅斯克近似会明显低估温度,未加大计算域可能导致纵向温度分布不对称,因此选取工况A4、B1 和B2 的顶棚下方最大温度做对比,顶棚下方最大温度如图5 所示,同时给出了Li 模型[31]的预测值。

图5 顶棚下方最大温度

可以看出,VHS 模型高估了顶棚下方最大温度,而MT-VHS 模型的预测结果与Li 模型很接近,误差在10%以内。因此,在使用FLUENT 软件模拟隧道火灾时,推荐使用MT-VHS 模型,且在定义空气性质时推荐使用拟合参数。

4 结论

针对FDS 无法捕捉复杂隧道结构的问题,本文基于Heskestad 羽流模型,提出了空气卷吸模型和传质体积热源模型,并选取典型隧道火灾场景,比较了不同物理模型、燃烧模型、气体描述模型的计算结果,最后将模拟结果与缩尺试验相比较,筛选出了科学经济的CFD 模型。具体结论如下:

(1) 在隧道两端出口加大计算域能够消除不合理的边界条件对隧道内温度场的影响。隧道端口存在中性面,因此端口处的压强必定有变化,而不扩大计算域的物理模型,简单地将端口处的压强认为是一个常数不够合理。数值模拟结果也表明,若没有加大计算域,隧道顶棚下方温度纵向分布可能变得不对称。隧道壁厚对温度影响不大。

(2) 空气热物性参数决定了隧道内的温度场。其他模型设置相同时,布辛涅斯克近似给出的隧道内温度较低,拟合参数给出的温度较高。布辛涅斯克近似假设空气性质不变,但实际上随着温度的升高,空气密度降低,导热系数增大,导致空气的热扩散系数增大,使顶棚温度急剧升高。由于没有考虑壁面散热,使用空气拟合参数计算得到的温度较高。

(3) 加大计算域、燃烧模型采用MT-VHS 的设置能够给出隧道顶棚下方最大温度较好的预测值,本文的误差在10%以内。但是该模型没有考虑壁面的散热和空气卷吸,因此给出的纵向温度分布比试验值高。

本文选取了典型火灾场景,对比了不同CFD 模型的计算结果,确认了传质体热源模型的科学性和经济性,为复杂隧道内火灾的数值模拟提供了科学的方法。虽然该模型对顶棚下方最大温度的预测较准确,但是对纵向温度分布的预测值偏大,需要考虑对流换热系数。此外,通风情况下的火羽流形态和空气卷吸发生改变,传质体积热源模型中的质量传递的量以及火焰长度和倾斜角度需要修正,此外,本文没有考虑火焰触顶的工况,将作为下一步的研究方向。