基于机器学习的独柱墩桥梁抗倾覆性能研究

周 童

(华设设计集团股份有限公司,南京 210014)

独柱墩桥梁因其结构轻巧、线条流畅、通透度高、占用空间小、施工便捷等优点,被广泛用于城市交通建设中。与预制简支箱梁桥相比,独柱墩桥梁具有更好的整体性能、更强的跨越能力以及更舒适的行车体验,因此在立交桥、高架桥分离式匝道以及上下引桥等建设工程中也得到广泛应用。

目前,独柱墩桥梁抗倾覆稳定性方面的研究主要集中在倾覆破坏机理、倾覆承载力计算方法以及倾覆影响因素分析等方面[1-4]。彭卫兵等[1]以浙江省的上虞春晖立交桥为研究对象,研究了独柱墩桥梁在超载和偏载作用下的2 个关键状态,并定义了倾覆的3 个阶段,即稳定阶段、过渡阶段和倾覆阶段。熊文等[3]以黑龙江省哈尔滨市的阳明滩大桥为例,利用精细化的三维有限元建模技术,提出了4 个依次发生的临界倾覆状态。曾燊平[4]以广明高速公路上的一座独柱墩箱梁桥为工程依托,建立了曲线梁桥空间分析模型,分析预应力荷载、桥梁曲线半径、联端支座间距等因素对独柱墩桥梁横向抗倾覆稳定性系数的影响程度。

在独柱墩桥梁设计的过程中,抗倾覆稳定性计算是一项重要工作。单向受压支座反力和横桥向抗倾覆稳定性系数[5]为计算重点。基于空间模型的有限单元法是一种相对准确的分析方法,并已得到广泛应用。此外,可利用独柱墩桥梁项目数据和适当的算法模型,预测出独柱墩桥梁抗倾覆稳定性系数的近似值。若经测试,该近似值的方差及偏差都很小,那么这种算法可以作为独柱墩桥梁抗倾覆稳定性快速判断和数据校核的一种有效手段。

本研究利用机器学习算法系列中的贝叶斯模型算法来预测独柱墩桥梁抗倾覆稳定性系数。与传统参照桥梁规范条文的有限元模型不同,采用贝叶斯模型算法得到的抗倾覆稳定性系数值是从大量设计及计算基础数据中推测的经验值。虽然相关机器学习算法已经在桥梁抗震设计评价、梁桥变形预测等方面得到应用[6-7],但基于贝叶斯模型算法预测独柱墩桥梁的抗倾覆稳定性系数的相关研究较少。

本研究总结了当前独柱墩桥梁抗倾覆稳定性系数的分析方法,对比常用机器学习算法的优缺点,探讨贝叶斯模型算法的原理和实现路径,旨在为类似独柱墩桥梁工程的设计与加固工作提供参考。

1 桥梁抗倾覆稳定性系数分析方法

随着失稳效应的逐渐增强,独柱墩桥梁倾覆过程中存在2 个关键状态,即箱梁的单向受压支座开始脱空和箱梁的抗扭支承全部失效[5]。

根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018),独柱墩桥梁抗倾覆稳定性验算的流程为:建立独柱墩桥梁有限元模型→计算永久作用标准值效应→计算最不利汽车荷载的标准值效应→验算作用基本组合下支座反力→计算稳定效应→计算失稳效应→计算标准值组合下抗倾覆稳定性系数,并与规范限值(2.5)进行比较。稳定效应计算公式如式(1)所示,失稳效应计算公式如式(2)所示,标准值组合下抗倾覆稳定性系数计算公式如式(3)所示。

式中,li为第i个桥墩处失效支座与有效支座的支座中心间距;RGki为在永久作用下,第i个桥墩处失效支座的支反力;RQki为在可变作用下,第i个桥墩处失效支座的支反力。

2 贝叶斯模型算法

2.1 机器学习算法对比

贝叶斯模型算法作为机器学习的一种常用算法,通过贝叶斯定理估计模型参数,并给出对未知变量的预测分布。相较于传统的线性回归、决策树等方法,贝叶斯模型算法可以更好地处理噪声、过拟合等问题,并且可利用先验信息进行预测和不确定性分析[8]。常用机器学习算法对比如表1 所示。

表1 常用机器学习算法对比

结合独柱墩桥梁抗倾覆稳定性系数的特点,综合考虑样本容量、特征数据相关性、预测稳定性等因素,本次选取贝叶斯模型算法进行预测。

2.2 贝叶斯回归算法原理

贝叶斯回归算法的核心思想是基于概率框架将所有未知变量都视为随机变量,并从先验分布开始不断根据观测数据进行更新。具体而言,假设预测目标y是一个连续随机变量,输入变量x是一个向量,那么贝叶斯回归可表示为

式中,p(y|x,θ)为条件概率分布,表示在已知输入变量x和模型参数θ的情况下,输出变量y的概率分布;p(θ|D)为后验概率分布,表示在已知观测数据D的情况下,参数θ的概率分布;D为观测数据集合。

在贝叶斯模型算法中,可以通过构建模型来确定参数θ的先验概率分布和似然函数,并利用贝叶斯定理计算后验概率分布。具体而言,可使用马尔科夫蒙特卡洛方法采样后验概率分布,或使用变分推断等方法近似计算后验概率分布。最终通过后验概率分布对未知参数进行估算,并使用估算结果进行预测或决策。

2.3 算法实现

采用Python 编程软件编制独柱墩桥梁抗倾覆稳定性系数预测的程序,流程如下。

(1) 定义先验分布:定义高斯先验分布,描述目标变量y(即抗倾覆稳定性系数kqf)与特征变量x之间的关系。

(2) 计算后验分布:根据贝叶斯公式计算权重向量w的后验分布,即p(w|x,y,α,β)。此处需要计算数据的似然函数p(y|x,w,β)和先验分布p(w|α),并利用高斯分布的性质得到后验分布p(w|x,y,α,β)。

(3) 进行预测:对于新的输入特征向量xtest,根据后验分布计算条件分布p(ytest|xtest,x,y,α,β),并求其均值或中位数等作为模型预测结果。

在具体实现时,可以使用Scikit-learn(基于Python 语言的机器学习工具)库中的BayesianRidge(贝叶斯岭回归)类来实现计算流程。该类采用coef_(权重)属性和intercept_(截距)属性获取模型系数和截距等信息。贝叶斯模型算法的Python 程序计算流程如图1 所示。

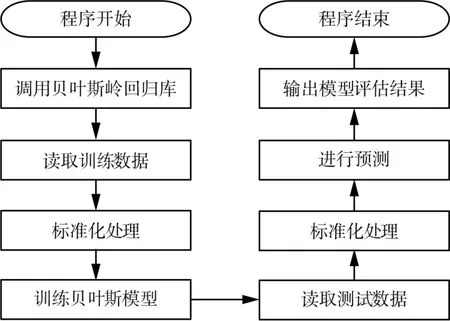
图1 贝叶斯模型算法的Python 程序计算流程

3 应用分析

采用贝叶斯模型算法预测独柱墩桥梁抗倾覆稳定性系数时,须进行的步骤如下。

(1) 准备样本数据:收集大量独柱墩桥梁的相关数据,包括设计参数、抗倾覆计算结果。将这些数据整理成可用于训练和测试的数据格式。

(2) 学习训练并建立预测模型:运用贝叶斯模型算法对样本数据进行学习和训练,以建立用于预测的模型。

(3) 模型测试:利用已有的样本数据对预测模型进行测试,评估模型的预测能力和准确度。可以采用交叉验证等方法来检验模型泛化能力和稳定性。

通过相关步骤,可利用贝叶斯算法快速预测独柱墩桥梁的抗倾覆稳定性系数。需要注意的是,在样本数据的准备和模型训练过程中,应保证数据的质量和充分性,避免过拟合等问题。同时,在应用预测模型时,需要对新数据进行验证和检验,以保证预测结果的可靠性和有效性。

3.1 样本数据准备与训练

样本数据是指实际场景中采集到的数据样本,也可以是通过模拟等方式生成的数据。在机器学习领域,样本数据是构建模型和进行模型训练的基础,对于模型的性能和预测能力起着至关重要的作用。样本数据通常包含输入特征和输出标签两部分,其中输入特征是描述样本属性的数值或向量,而输出标签则是需要预测或分类的目标变量。

独柱墩桥梁抗倾覆稳定性系数的影响因素较多,包含桥梁联长、边中跨比、平曲线半径、桥宽、联端支座间距、预应力荷载、独柱墩支座预偏心等[4]。为提高预测精度同时简化分析,本研究选取桥梁联长L、平曲线半径R、桥宽B、扭转跨径l(桥梁相邻抗扭支承之间的跨度)及联端支座间距b共5 个特征参数。训练样本数据如表2 所示,抗倾覆稳定性系数kqf的规范值表示标签数据。

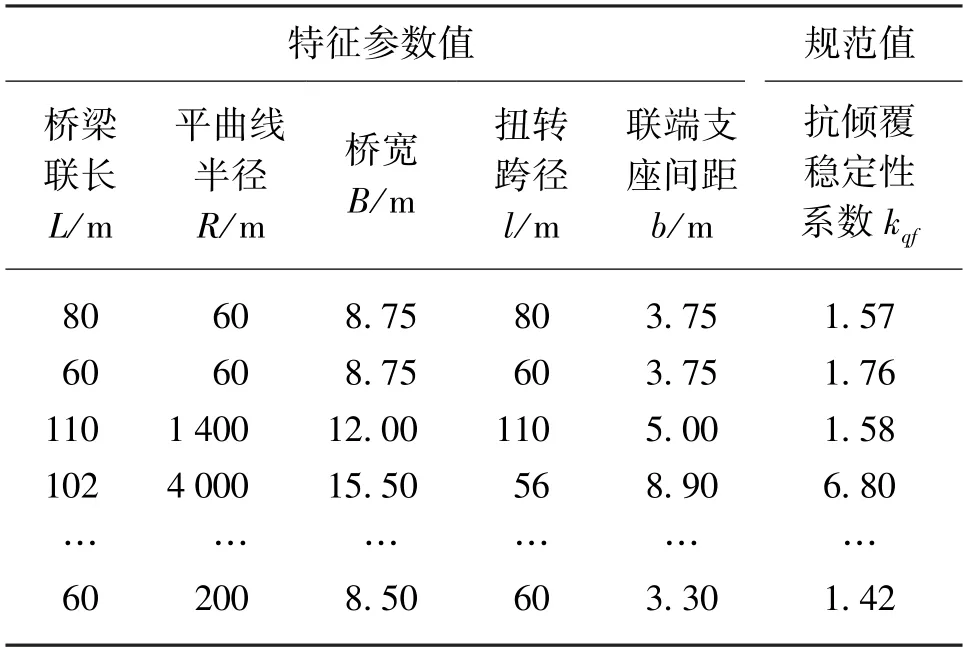
表2 训练样本数据

利用表2 中的样本数据对基于Python 语言编写的贝叶斯模型程序进行训练,得到贝叶斯模型基本参数。特征1～5 的模型系数(即模型中各特征对应的权重)分别为-0.56(桥梁联长L系数)、0.44(平曲线半径R系数)、-0.37(桥宽B系数)、-3.42(扭转跨径l系数)和0.76(联端支座间距b系数)。由特征系数可知,独柱墩桥梁的抗倾覆稳定性系数与桥梁联长、桥宽、扭转跨径负相关,与平曲线半径、联端支座间距正相关,且扭转跨径对倾覆系数影响的权重最大,设计时应合理控制独柱墩的数量,不宜采用连续的单支座结构。

3.2 数据测试

为评估贝叶斯模型算法用于独柱墩桥梁抗倾覆稳定性系数预测的适用性,需要利用测试数据对其进行验证。部分测试数据的预测结果与规范计算值的对比情况如表3 所示。

由表3 可知,利用贝叶斯模型算法预测的抗倾覆稳定性系数值与规范计算值误差较小,其均方误差(所有数据点误差平方的平均值)为0.72,决定系数(系数越接近1,模型对数据的拟合程度越好)为0.92,预测结果较好。贝叶斯模型预测值与规范值残差图如图2 所示。

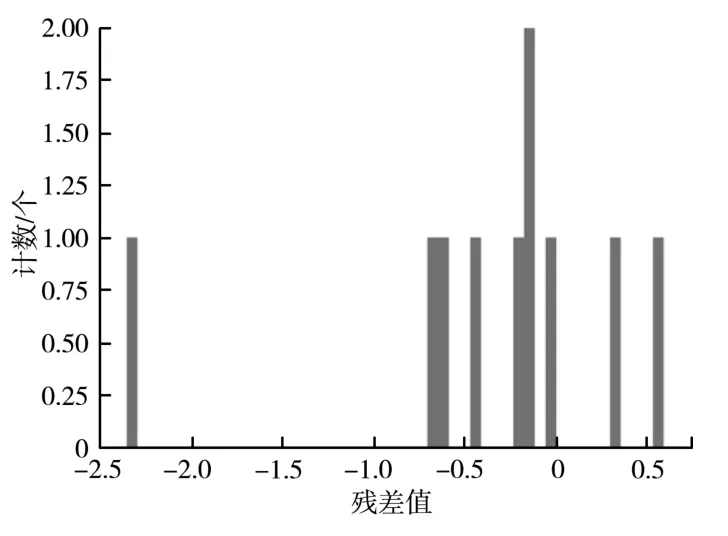
图2 贝叶斯模型预测值与规范值残差图

由图2 可知,测试数据中除1 个样本残差较大外,其余数据残差大致位于-0.5～0.5 之间,表明贝叶斯模型不易受到噪声或异常点的影响,能更好地应对数据变化、分布改变等情况,具有更好的鲁棒性和稳定性。

4 结论

(1) 贝叶斯模型算法是一种机器学习算法,可以用于独柱墩桥梁抗倾覆稳定性系数的预测。尽管这些预测值本质上是基于工程经验推算出的近似值,但贝叶斯模型算法的预测误差较小,因此可将其作为快速判断和校核的工具进行应用。

(2) 独柱墩桥梁的抗倾覆验算与桥梁联长、平曲线半径、桥宽、扭转跨径、联端支座间距等因素密切相关,设计阶段应综合考虑各项因素,提升设计的合理性。

(3) 贝叶斯模型算法不仅在独柱墩桥梁抗倾覆稳定性系数的预测方面具有应用价值,还可广泛应用于桥梁工程领域的其他相关预测中,例如施工及运营阶段的变形预测、抗震性能评价及桥梁动态称重系统应用等方面。该方法充分利用相关设计、施工中积累的大量现有数据,具有较高的使用价值且应用前景广阔。