防振锤抑制吊索涡激振动的优化设计方法
于 力
(南京长江第二大桥有限责任公司,南京 210043)
在悬索桥及下承式拱桥工程中,吊索作为主要传力构件被大量使用。然而,吊索的横向刚度小且自身阻尼低,很容易受到外界激励发生振动,其中最常见的是风荷载导致的吊索涡激振动[1-2]。长期振动会缩短吊索的寿命,危及桥梁安全,也会造成行人的恐慌。在斜拉桥工程中,通常采用改变索的气动外形[3]、安装索端阻尼器[4-6]及连接索间辅助索[7-8]等方法进行拉索减振,这些措施也被扩展应用到吊索减振中[9-10]。
阻尼器是目前最常用的拉索减振设备,也被应用在吊索减振中[11]。在斜拉桥工程中,阻尼器通常被安装在索的端部,一端连接在索上,另一端连接在桥面伸出的支架上。然而,吊索与斜拉桥拉索布置形式不同,一般垂直安装,因此对于吊索而言,阻尼器及其支架的安装较为困难,也会影响桥梁美观。特别是对于长吊索,为了满足减振要求,阻尼器需要较大的安装高度;同时,考虑到支架柔度对阻尼器减振效果的不利影响,实桥阻尼器支架往往较粗大[5]。综上,阻尼器需要安装支架的问题限制了其在吊索减振中的应用。
调谐质量阻尼器(tuned mass damper,TMD)作为一种拉索减振设备,可安装在拉索的任意位置,在吊索减振方面具有优势[10]。防振锤作为一特殊形式的TMD 装置,最初被应用于高压输电线的减振中,其主要由锤头、钢绞线和夹具3 部分组成,通过夹具与输电线连接。这种装置也被用于摩天轮轮辐式缆索、体育场支承索以及桥梁缆索等各种结构中,各种实际工程应用验证了防振锤对拉索减振的有效性。目前,在桥梁工程领域,防振锤已被用于斜拉桥拉索、悬索桥吊索等索类构件的减振,比如韩国的巴龙悬索桥、平泽斜拉桥,中国的南沙大桥等[11]。
采用防振锤进行吊索减振具有其优势和应用前景,然而,目前关于拉索防振锤的系统研究较少,相关设计方法也鲜有介绍。为此,本文基于能量平衡方法提出了吊索-防振锤减振的优化设计方法,并针对实际桥梁的吊索进行了案例设计分析,研究成果可为实际工程中的吊索防振锤设计提供指导。
1 理论推导
1.1 能量平衡方法
采用能量平衡方法评估吊索振动。该方法认为,吊索和防振锤消耗的能量之和与风带来的能量相同[12],可以表示为
通过求解式(1),可以得到风荷载作用下的吊索振动响应幅值。
1.1.1 风作用能量
基于风洞试验,学术界提出了多种不同的风能计算公式[13]。本文选用其中的一种计算公式:
式中,L为吊索长度,m;f为振动频率,Hz;D为吊索直径,m;A为吊索振动幅值,m。
1.1.2 拉索耗能
基于拉索振动试验,学者提出了各种拉索耗能公式[14]。本文选取的公式为
式中,K为比例系数;T为吊索索力,N。
1.1.3 防振锤耗能
防振锤消耗的能量可以由下式得到:
式中,Z为阻抗,表示防振锤出力与速度之比;为防振锤锤头最大速度;α为防振锤出力与速度之间的相位滞后(相角)。吊索由防振锤消耗的能量计算公式如下[15]:
式中,k=为波数;为波速;γ=T/ZCw;l1为防振锤的安装位置。防振锤的动力参数即阻抗(Z)和相角(α),可以通过两自由度模型得到。
1.2 防振锤动力特性
为了采用能量平衡方法评估吊索的振动,首先需要知道防振锤的动态特性Z(阻抗)和α(相角)。为了确定这些特性,防振锤模拟为二自由度系统[16],防振锤模型如图1 所示。图中,y1为吊索振动幅值,x1和x2分别为钢绞线末端位移和转角,L是钢绞线的长度,l为钢绞线末端与质心之间的距离。
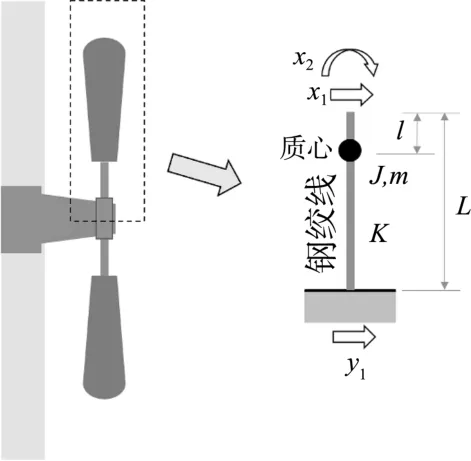
图1 防振锤模型
假设钢绞线为无质量悬臂梁,则可获得K(刚度矩阵)。假定锤头为集中质量,作用于质心位置。在此基础上,建立防振锤的运动方程:
式(7)可写成如下形式:
利用式(8) 可以得到
最后,防振锤的动态特性可以表示为
进一步,Z(阻抗)和α(相角)可以由下式得到
2 防振锤设计
2.1 设计流程
根据第1 节的理论,得到防振锤的设计流程如图2 所示。首先,根据吊索参数和桥址风环境(风速)确定吊索可能发生涡激振动的频率范围,即确定吊索需要控制的振动模态阶次。选择合适的防振锤产品,利用前文的理论建立吊索-防振锤系统模型,计算安装防振锤后吊索的最大振幅。计算安装防振锤后能否满足吊索振幅控制的要求,如不满足,则改变防振锤型号或安装位置并重复上述计算,直至满足要求。通过试算,最终确定防振锤的安装位置和型号。需要注意的是,在实际工程中,防振锤安装位置的确定不仅需要考虑减振性能,还需要考虑安装与维护的方便,因此,在满足振幅控制要求的前提下,防振锤应尽可能靠近桥面安装。对于实际吊索的宽频段振动,可以考虑安装多个防振锤的方案,可同样采用本文的设计方法分别进行防振锤的设计。
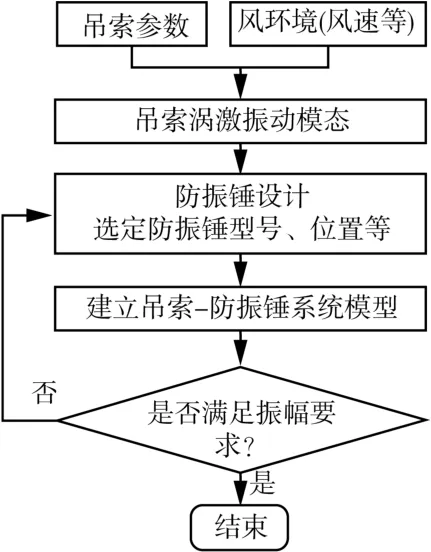
图2 防振锤的设计流程
2.2 算例吊索
选取某桥两根不同长度的吊索,进行防振锤的设计。吊索参数如表1 所示。

表1 吊索参数
2.3 振控目标频率范围
描述物体周围可压缩流体(如吊索周围的风)流动的一个关键参数是雷诺数(Reynolds number)。雷诺数是风惯性力与黏性力之比的量度,由下式给出:
式中,ρ为空气密度,kg·m-3;V为风速,m·s-1;μ为空气黏度,g·(m·s)-1。对于本文算例,ρ取1.25 kg·m-3,索直径D为0.055 m,μ取1.875×10-5。统计数据表明,3 级风在桥梁现场最为常见,因此,防振锤主要用于控制吊索在3.4 m·s-1至5.4 m·s-1风速范围内可能发生的涡激振动。相应地,雷诺数分别按下式计算:
换言之,桥址处吊索的雷诺数范围为1.25×104~1.98×104。
斯特劳哈尔数(Strouhal number)是一个无量纲参数,其计算公式为
式中,NS为涡激频率。
根据美国联邦公路管理局(US Federal Highway Administration)的报告,斯特劳哈尔数在风速的扩展范围内保持不变。当雷诺数在1×104~3×105范围内时,吊索的斯特劳哈尔数值(S)可设置为0.2。
当涡脱频率与吊索的固有频率一致时,吊索将发生涡激振动。将吊索的固有频率代入式(13),可以计算涡激风速V:
式中,NS等于吊索的固有频率f。
用于计算吊索频率的公式如下:
式中,T为吊索索力,kN;m为单位长度质量,kg·m-1。
根据表1 中的吊索参数,可计算出该桥吊索可能发生涡振的风速以及对应的模态频率。吊索涡振风速如表2 所示。

表2 吊索涡振风速
由表2 可知,H1 号吊索可能发生涡振的阶次是第5 阶到第7 阶;H2 号吊索可能发生涡振的阶次是第8 阶到第12 阶。因此,防振锤应根据对应阶模态进行设计。
2.4 防振锤设计
选择一种防振锤,防振锤设计如图3 所示。防振锤参数如表3 所示。

表3 防振锤参数
图3 防振锤设计
2.5 防振锤设计结果
为了便于安装及日常维护,在吊索上安装两个防振锤,分别位于距离索桥面锚点3 m 处和4 m 处。当两个防振锤安装在目标吊索时,采用能量平衡方法评估涡激振动下吊索的振幅,并由二自由度模型获得动力学特性。假设吊索的允许振幅为D/10(5.5 mm)。安装防振锤前后吊索的振幅对比如图4 所示。
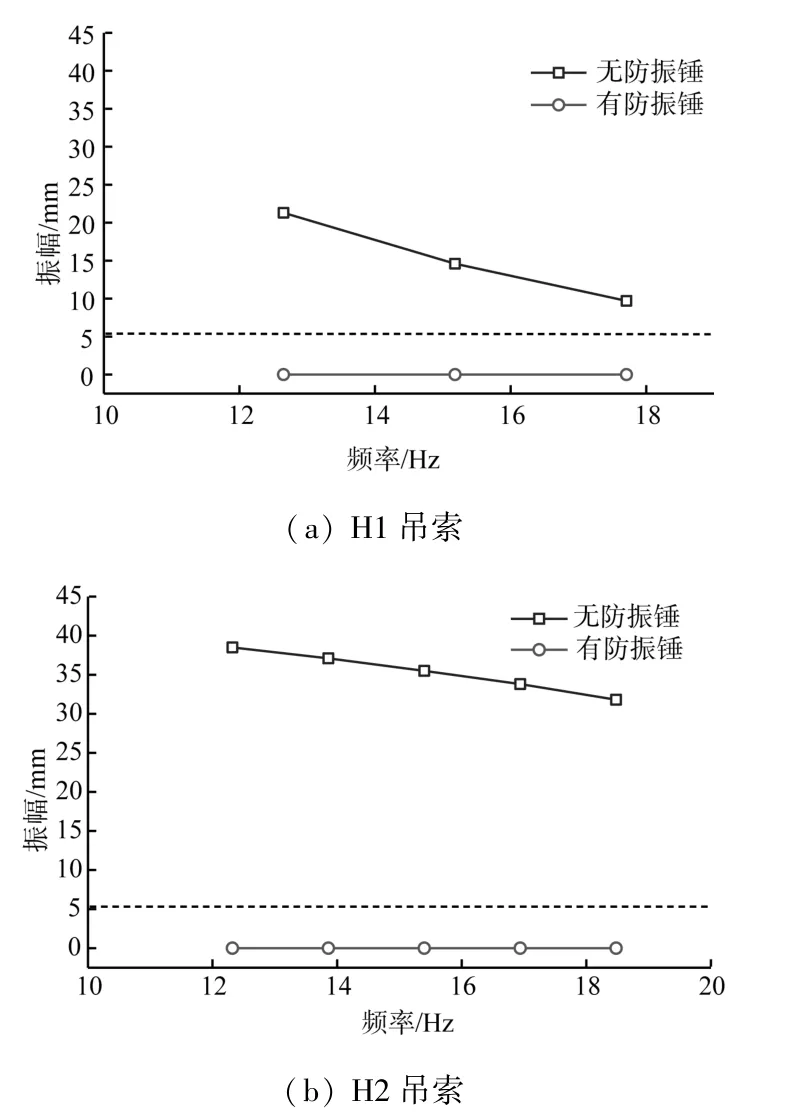
图4 安装防振锤前后吊索的振幅对比
由图4 可以看出,由于防振锤对吊索易振频率区段的调谐较好,安装防振锤后,吊索的振动幅值显著降低,由此可知本文设计的防振锤能够控制所有目标阶模态的振动。
3 结论
本文建立了吊索-防振锤的系统理论模型,在此基础上,提出了防振锤抑制吊索涡激振动的设计流程。以吊索振幅为控制指标,通过吊索所处风环境及自身参数确定其需控模态,利用能量平衡方法计算吊索安装防振锤后的振动幅值,最终确定防振锤的安装位置和型号。
选取两根实桥吊索为算例,采用本文提出的方法进行防振锤的设计,计算结果验证了防振锤控制吊索涡振的有效性,并验证了本文设计方法的可行性。本文提出的防振锤设计方法可为悬索桥、拱桥等工程的吊索减振设计提供参考。

