基于光谱色差权重函数的多光谱降维方法研究
曹 前, 麻祥才, 白春燕, 苏 娜, 崔庆斌
上海出版印刷高等专科学校印刷包装工程系, 上海 200093
引 言
光谱反射率维度高, 与光照和观察条件无关, 能够客观、 真实地描述物体的颜色信息, 是物体本身特性决定的, 因此被称为物体的“指纹”, 在光谱颜色复制[1]、 纺织[2]等领域受到广泛关注。 但是, 用于光谱颜色复制领域的光谱数据通常选取10 nm间隔的400~700 nm波段的共计31维数据组成。 其数据量超过传统三色颜色系统十倍以上, 这些巨大的光谱数据在存储、 数据处理和数据传递等方面造成巨大的负担, 花费太多的计算时间。 如果高维光谱可以通过数学变换方法映射到低维空间, 并确保低维空间数据能够更好地表示原始光谱所覆盖的信息, 可以有效地压缩多光谱数据, 提高多光谱色彩再现的处理效率。 因此, 光谱数据压缩或者光谱数据维度降低成为光谱颜色复制的一项关键技术。 已经有大量数据维度降低算法应用到高维光谱降维, 如主成分分析(principal component analysis, PCA)、 压缩感知算法[3]、 box-cox变换[4], 神经网络[5]等。 物体表面的反射率光谱通常是由可见光范围内波长的光滑函数组成, 这些光谱强烈相关并可以由少量的正交基函数组成, 主成分分析法正是基于这个事实来实现多光谱数据降维。 因此, 基于PCA的多光谱数据压缩算法引起了广泛关注, 国内外开展了大量相关研究。 但是, 主成分分析法平等地对待可见光范围的所有波长, 重建光谱仅仅是对原始光谱的数学逼近, 由于根据波长对颜色的重要性不同, 经常会导致光谱误差较小而颜色色差较大。 为了克服这个缺点, 主成分分析法应该根据波长对颜色的重要性进行修改, 更确切地说, 如果光谱数据的某些部分对颜色值不太重要, 就可以增加相应的权重来减少这部分光谱对颜色影响。 已经有一些研究者提出权重的主成分分析法来进行光谱数据降维, 具体来说, 就是在形成相关矩阵和计算特征值之前将光谱数据乘以适当的系数或者权重函数。 为了尽可能减少光谱维度降低过程中颜色信息的损失, 不同的学者从理论推导和大量实验基础上, 提出了基于颜色匹配函数、 视锥细胞响应函数和光谱变化引起的色差等方面提出了不同的权重函数。 Laamanen等[6]于2008年提出基于颜色匹配函数的权重函数的权重主成分多光谱降维算法。 王莹等[7]于2011年提出一个基于代表人眼平均视觉特性的颜色匹配函数的权重函数。 Tian等[8]于2013年建议基于颜色匹配函数的不同组合的多光谱降维算法的权重函数; Wu等[9]于2015年提议基于人眼视觉特性的颜色匹配函数之和的平方根作为多光谱降维算法的权重函数; Cao等[10]于2016年也提出颜色匹配函数的平方根之和作为多光谱降维算法的权重函数; 刘士伟等[11]于2017年构建基于视锥细胞响应函数不同组合的权重函数。 梁金星等[12]提出基于视觉特征函数的权重函数; Ma等[13]于2020年构建了另外一个基于色差变化的权重函数用于保留更多的颜色信息。
上述学者提出的权重函数在确保光谱精度可以接受的条件下, 显著地提高了光谱降维和压缩过程的色度精度, 保留了更多的颜色信息, 对于多光谱色彩复制有非常积极意义。 可是, 上面提到的权重主成分分析法, 当改变测试样本或是使用其他光谱图像数据时, 其色度误差仍然不可忽视, 对于在光谱颜色复制领域中的实际应用还有很大的距离。 在多光谱图像通过降低维度进行压缩过程中寻找一个保留更多颜色信息的权重函数对于光谱颜色再现具有重要现实意义。
本文提出了一种基于光谱色差的权重函数的多光谱降维算法, 权重函数由光谱数据集原始光谱和该光谱数据集重建光谱之间的平均光谱色差构成。 本研究以NCS为训练样本, 分别以NCS、 Munsell和3张多光谱图像测试和对比本文推荐的方法和主成分分析法以及另外4种权重主成分在多光谱降维过程中的性能; 利用公式将测试样本压缩到低维光谱空间, 再利用公式将低维光谱数据恢复还原到高维光谱。 以CIELAB色差和均方根误差(RMSE)来评价测试样本的原始光谱和恢复光谱之间的色度误差和光谱误差。
1 实验部分
1.1 权重主成分分析
一组光谱数据矩阵, 设采样维度为n, 样本数为p, 用矩阵S表示这个光谱数据集。 定义对角矩阵W, 其对角线元素由权重函数w(λ)组成。 光谱矩阵S乘以矩阵W, 权重光谱矩阵SW由式(1)表示
SW=WS
(1)
权重光谱矩阵SW的相关系数矩阵ΣW如式(2)所示
(2)
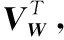
(3)
(4)
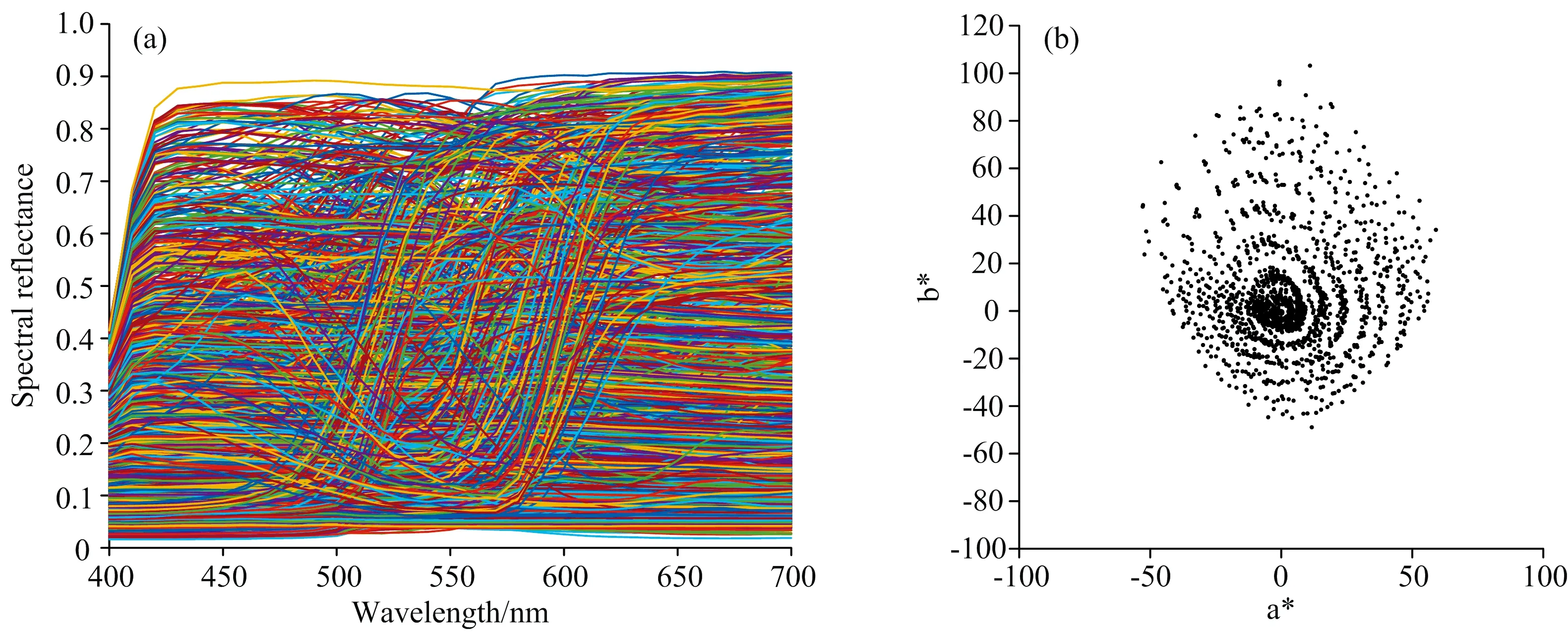
式(4)中, inv(W)表示方阵W的逆矩阵。
1.2 光谱色差公式
根据文献[14-15], 本文定义光谱色差如下: 任意一个光谱反射率在可见光范围内各个波段的色差, 其计算公式如式(5)所示。 式中,L(λ)、a(λ)和b(λ)的计算公式如式(6)、 式(7)和式(8)所示。
ΔE(λ)=
(5)
(6)
(7)
(8)
其中,
(9)
其中,u依次替换为物体的三刺激值X、Y、Z,un依次替换为参考光源的三刺激值Xn、Yn和Zn,S(λ)表示光源的相对光谱功率分布,k表示使得参考光源的Yn等于100时的系数。
1.3 权重函数的构造
1.3.1 权重函数构成思路和方法
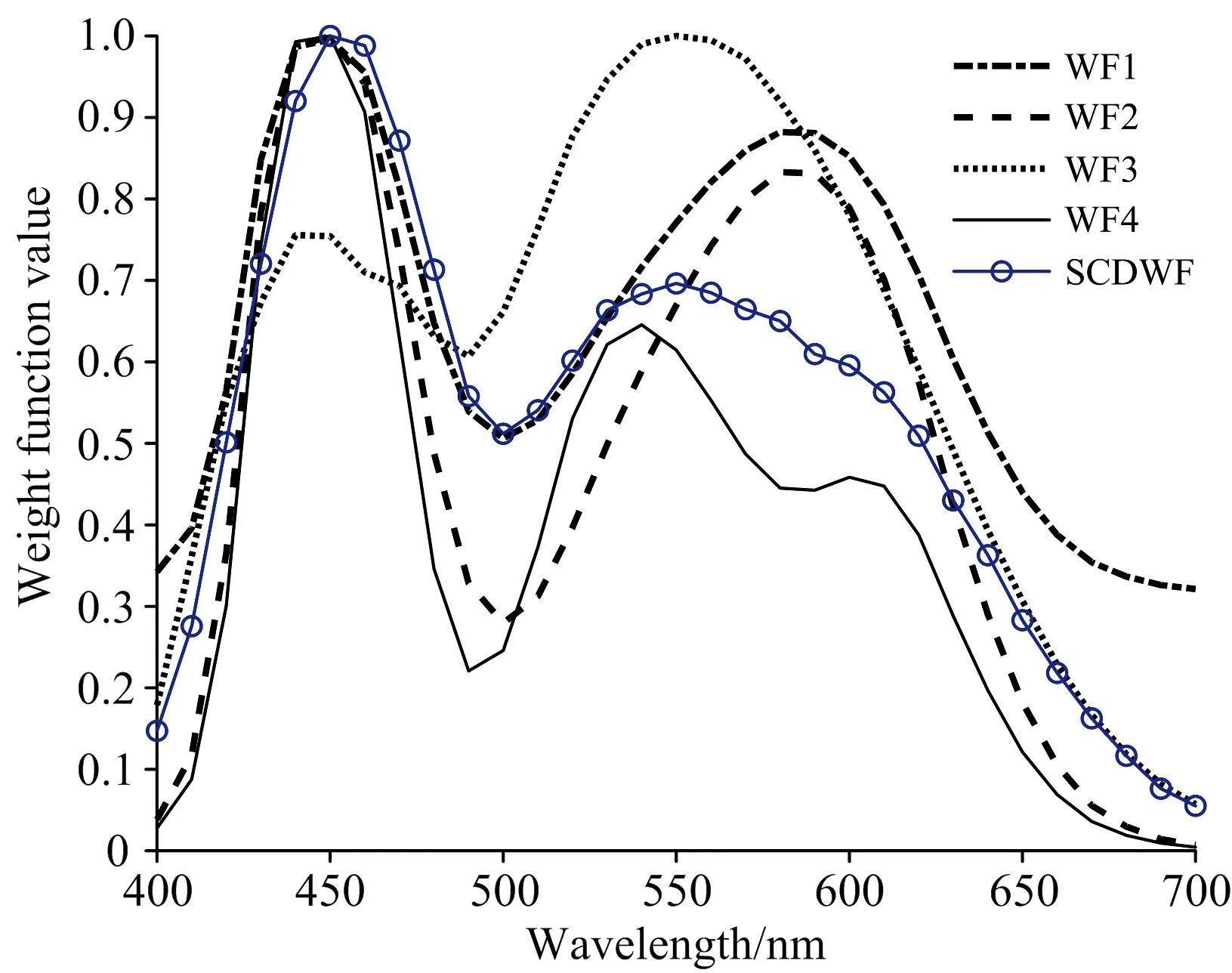
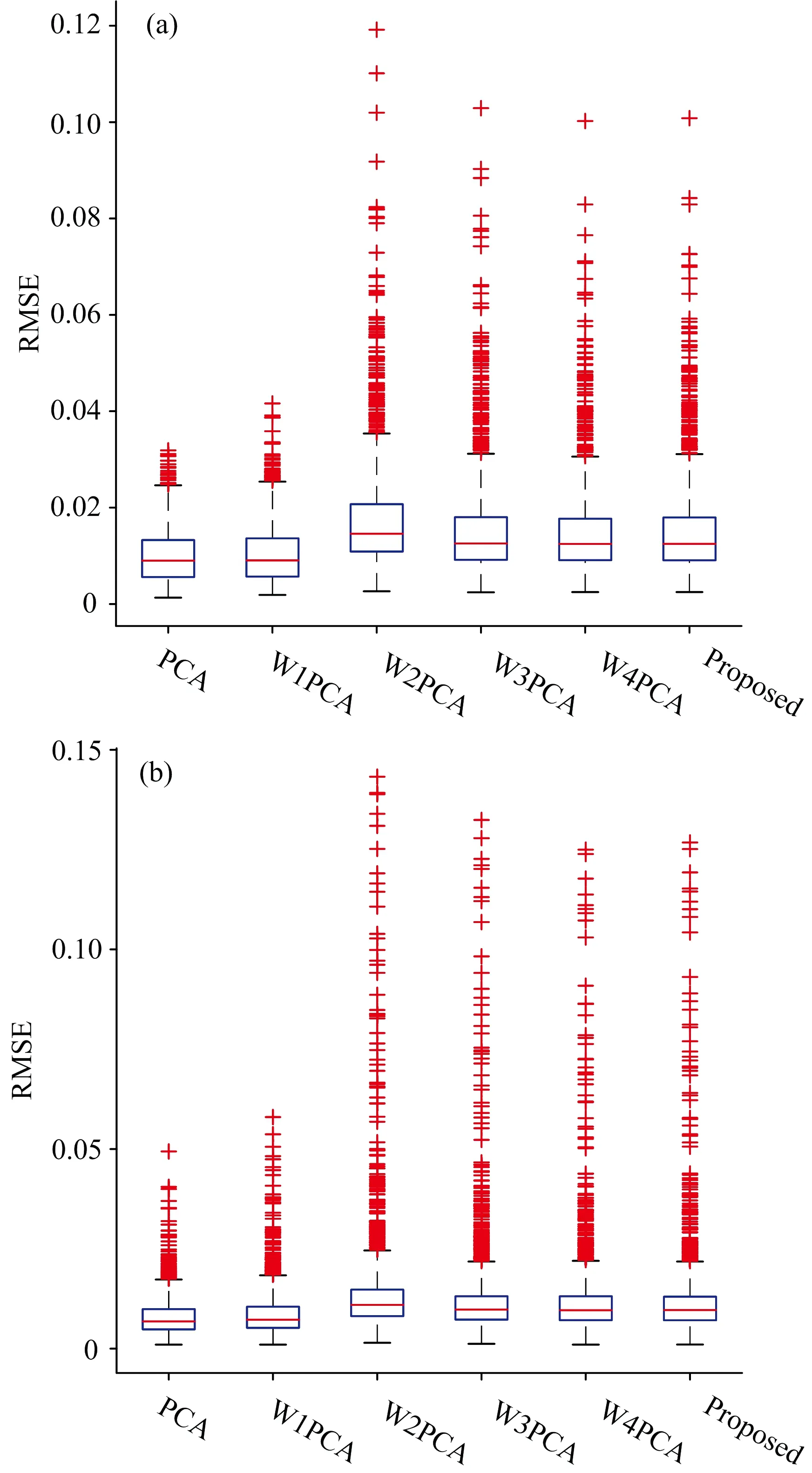
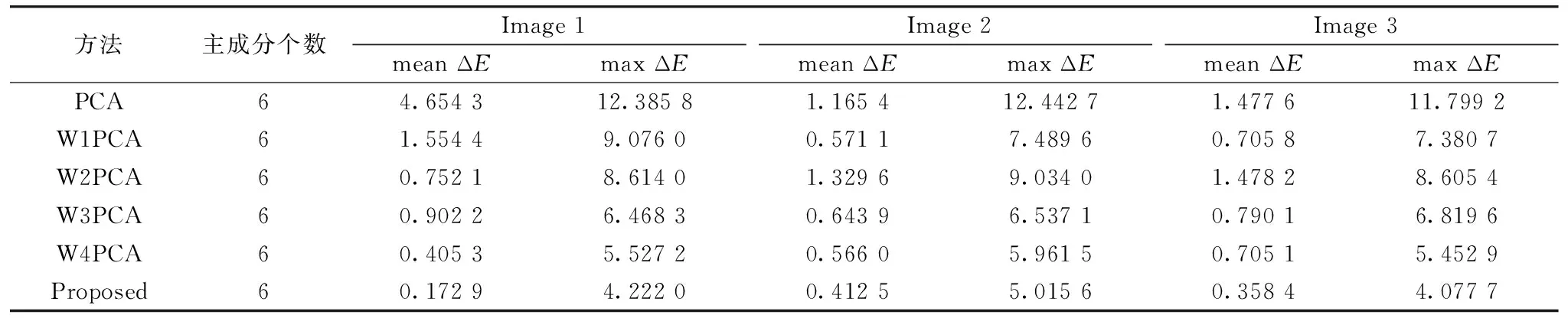
定义光谱数据集R的采样维度是n, 样本个数为p, 由光谱反射率r1,r2, …,rp组成, 如式(10), 采用主成分分析对其降低维度到m(m R=[r1r2…rp] (10) (11) 1.3.2 权重函数的计算 通过大量的测试, 本文选取有1 600个光谱组成的Munsell数据集作为R, 使用主成分分析法降低维度到1维, 再恢复到31维, 得到光谱数据集R′, 全色差公式计算使用的参考光源为等能白光E, 根据权重函数构成思路和方法, 经过归一化后, 权重函数值如表1所示。 为了便于表达, 本文提出的权重函数命名为SCDWF, 对应的权重主成分命名为SCDPCA。 表1 由Munsell光谱数据集的原始光谱和恢复光谱的平均光谱色差构成的权重函数值(SCDWF) 为了光谱压缩过程中保留更多的颜色信息, Laamanen等[6]于2008年提出一个基于颜色匹配函数的权重函数, 命名为WF1, 如式(12)所示, 其对应的权重主成分命名为W1PCA。 (12) Tian等[8]于2013年也提议基于人眼视觉特性的颜色匹配函数的不同组合的权重函数, 命名为WF2, 如式(13)所示, 其对应的权重主成分命名为W2PCA。 (13) 刘士伟等[11]于2017年构建基于视锥细胞响应函数不同组合的权重函数, 命名为WF3, 如式(14)所示, 其对应的权重主成分命名为W3PCA。 (14) 式(14)中,L(λ),M(λ)和S(λ)分别表示感红、 感绿和感蓝三种视锥细胞响应函数。 Ma等[13]于2020年构建了另外一个基于微小波长变化引起的色差的权重函数, 命名为WF4, 其对应的权重主成分命名为W4PCA。 本文推荐的权重函数和其他4种权重函数曲线如图1所示。 图1 本文推荐的权重函数SCDWF和其他4种权重函数曲线 本文使用两个著名的显色系统孟塞尔系统Munsell[16]和自然颜色系统NCS的色卡的光谱数据作为实验数据, 它们分别是有1 600和1 950色卡构成, 这些光谱数据都是用分光光度计测量得到, 它们的光谱反射率和对应的色度坐标如图2和图3所示。 来自哥伦比亚大学[17]的3张多光谱图像也作为本实验的测试样本, 图4显示这3张多光谱图像, 每张多光谱图像的分辨率都是512像素×512像素, 共计262 144个像素构成。 图2 照明观察D65/ 2°条件下(a)NCS的光谱反射率及其在CIELAB空间(b)中对应的a*b*图 图3 照明观察D65/2°条件下(a)Munsell的光谱反射率及其在CIELAB空间(b)中对应的a*b*图 图4 来自哥伦比亚大学的3张多光谱图像 首先, 使用本文推荐的方法和已经存在的方法分别通过训练样本NCS得到6维特征向量; 其次, 通过式(3)将31维的测试样本NCS、 MUNSELL和3张多光谱图像压缩到6维低维空间, 再通过式(4)将测试样本的6维低维空间数据还原到31维。 然后, 使用光谱精度和色度精度评价测试样本的原始光谱数据和压缩后再恢复的光谱数据之间的误差。 最后, 比较本文推荐的方法和已经存在的方法性能优劣。 原始光谱和压缩后恢复光谱之间存在误差, 该误差主要通过色度和光谱两个指标来评价。 原始光谱和压缩后恢复光谱的光谱精度的色度精度采用1976CIELAB色差评估, 色差小表示色度精度高。 原始光谱和压缩后恢复光谱的光谱精度通过均方根误差(root mean squared error, RMSE)[18-19]来评价, 如式(15)所示。 (15) 对比了我们推荐的方法和一些已经存在的方法的色度精度和光谱精度。 以NCS光谱数据集为训练样本, 使用本文推荐的方法和一些已经存在的方法得到6维主成分, 分别以NCS、 Munsell和3种多光谱图像为测试样本, 利用式(3)将测试样本的维度降低到6维低维空间, 再利用式(4)还原恢复到31维光谱数据, 使用式(13)和式(14)评价测试样本的原始光谱数据和恢复光谱之间的色度精度和光谱精度。 表2统计了以NCS为训练样本, 测试样本NCS的原始光谱和重建光谱数据在D65/2°和A/2°照明观察条件下的平均色差和最大色差。 图5表示以NCS为训练样本, 测试样本NCS的原始光谱和重建光谱数据之间色差分布的箱形图(boxplot)。 从表2和图5可以看出, 本文推荐的权重主成分在D65/2°和A/2°照明观察条件下的色度精度不仅优于主成分分析法, 而且也优于其他4种权重主成分分析法。 图5 测试样本NCS的原始光谱和重建光谱之间的色差分布的箱形图(boxplot) 表2 以NCS为测试样本时推荐的方法和已经存在一些方法在D65/2°和A/2°照明观察条件下色度精度对比 表3统计了以NCS为训练样本, 测试样本Munsell的原始光谱和重建光谱数据在在D65/2°和A/2°照明观察条件下的平均色差和最大色差。 图6表示以NCS为训练样本, 测试样本Munsell的原始光谱和重建光谱数据之间色差分布的箱形图(boxplot)。 从表3和图6可以看出, 以NCS为训练样本, 以Munsell测试样本时的色度精度的统计结果和色差分布情况再一次验证以NCS为训练样本, 以NCS为测试样本时在色度精度方面的结论。 表3 以Munsell为测试样本时推荐的方法和已经存在一些方法在D65/2°和A/2°照明观察条件下色度精度对比 表4统计了测试样本NCS和Munsell的原始光谱和恢复光谱之间的平均均方根误差(mean RMSE)和最大均方根误差(max RMSE)。 图7表示测试样本NCS和Munsell的原始光谱和恢复光谱之间的均方根误差(RMSE)分布的箱形图(boxplot); 从表4和图7可以看出, 测试样本为NCS或Munsell时, 主成分分析法的光谱精度(RMSE)优于本文推荐的方法和其他4种权重主成分。 结合色度精度结论, 权重主成分的色度精度提高是以牺牲一定的光谱精度为代价。 但是, 色度精度提高对于光谱颜色复制有重要的现实意义。 图7 测试样本的原始光谱和恢复光谱之间的均方根误差(RMSE)的箱形图(boxplot) 表4 测试样本为NCS和Munsell时推荐的方法和已经存在一些方法的光谱精度对比 表5统计了以NCS为训练样本, 3张测试样本的原始光谱和重建光谱数据在D65/2°照明观察条件下的平均色差和最大色差。 表6统计了以NCS为训练样本, 3张测试样本的原始光谱和重建光谱数据在A/2°照明观察条件下的平均色差和最大色差。 表7统计了3张测试样本的原始光谱和重建光谱数据之间的平均均方根误差(mean RMSE)和最大均方根误差(max RMSE)。 表5 测试样本为3张多光谱图像时推荐的方法和已经存在一些方法在D65/2°照明观察条件下色度精度对比 表6 测试样本为3张多光谱图像时推荐的方法和已经存在一些方法在A/2°照明观察条件下色度精度对比 表7 测试样本为3张多光谱图像时推荐的方法和已经存在一些方法的光谱精度对比 从表5、 表6和表7可以看出, 当测试样本为3张多光谱图像时色度精度和光谱精度的统计结果与测试样本为NCS或者Munsell时的结论大致一致, 更进一步验证了本文推荐的权重函数的色度精度不仅优于主成分分析法也优于其他4种权重主成分分析法。 提出了基于光谱色差权重函数的多光谱降维方法, 权重函数由光谱数据集和该光谱数据集经由主成分重建光谱的平均光谱色差构成。 本研究以NCS为训练样本, 分别以NCS、 Munsell和3张多光谱图像验证本文推荐的方法和主成分分析法以及另外4种权重主成分在多光谱降维过程中的性能优劣; 结果表明: 对比于主成分分析法, 测试样本无论是多光谱数据还是多光谱图像, 本文推荐的方法在牺牲了一定光谱精度的情况下, 在D65/2°和在A/2°两种照明观察条件下的色度精度得到显著的提高。 实验统计结果也显示本文推荐的方法的色度精度优于目前已经存在的另外4种权重主成分。 本文提出的多光谱降维方法保留了更多的颜色信息, 适合于高维光谱的降维、 压缩和存储等, 为高维光谱数据到低维连接空间数据的映射方法提供参考, 对于基于光谱的颜色复制研究有很重要的意义。

1.4 其他研究者提出的权重主成分多光谱降维算法
1.5 实验数据


1.6 评价指标
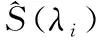
2 结果与讨论
2.1 色度精度比较



2.2 光谱精度比较

2.3 测试样本为3张多光谱图像时各种降维方法的色度精度和光谱精度对比


3 结 论

