考虑SVG控制模式的风电场系统中频谐振分析与抑制
陈继开,郝 鑫,常旗峰,李 平,李浩茹,初 壮
(东北电力大学 现代电力系统仿真控制与绿色电能新技术教育部重点实验室,吉林 吉林 132012)
0 引言
可再生能源大量接入使我国电力系统发展呈现高比例电力电子化趋势,而由此带来的诸如系统惯量降低、控制复杂度提升、宽频带谐振风险升高等问题已成为业内研究的焦点[1]。由于静止无功发生器(static var generator,SVG)具有灵活迅速补偿无功特点,被大量应用于新能源电站,通过动态无功调节,改善了区域系统的电能质量[2]。然而,当新能源电站位于电网末端时,其呈现弱系统特征,导致站内SVG 等并网变流器运行稳定性下降,在某些工况下系统发生谐振的风险增加[3]。
目前风电集中区域电网宽频带谐振问题正在凸显,例如:2012 年河北沽源风电场出现次同步谐振导致风机脱网问题[4];2015 年新疆哈密地区风电场也出现次同步谐振问题[5],导致火电机组扭振保护动作。针对此类问题,文献[4-5]分别利用特征值分析法、开环模式分析法,揭示了串补、弱电网以及控制器中锁相环参数整定不当是引发次同步谐振问题的主要原因。由于新能源电站中多配置了SVG,只针对风机与电网之间的交互问题进行分析,容易造成分析结果与实际工程不符,因此文献[6]基于特征值分析法,分析SVG 系统参数对直驱风电场次同步谐振的影响机理,发现SVG 系统参数取值与风电场区域系统谐振之间存在内在关联。然而在研究过程中并未考虑SVG 不同控制模式与系统谐振的关系,因此文献[7-8]分别采用阻抗分析法、特征值分析法,分析发现SVG 定电压控制模式比恒无功控制模式更容易引发系统次同步谐振。上述研究多关注于次同步频段谐振问题,而在后续研究中发现SVG 还会导致系统发生中高频谐振,例如:胡杨河地区含SVG 的光伏电站出现50 次高频谐振现象,导致大量电力电子设备损坏[9],因此专家学者开始关注由SVG引发的系统中高频谐振问题。以配置SVG和并联电容器组的双馈风电场为背景,文献[10]通过建立风电场阻抗模型,分析风电场出现的中频(200~500 Hz)谐振问题,指出与电容器组并联的SVG,如果其无功外环控制参数设置不合理,则可能导致系统在中频段进入负阻尼区域,继而引发谐振问题,但只分析了定电压控制模式,缺少其他控制模式对中频段谐振问题影响分析。文献[9]研究了含SVG 的新能源电站高频谐振问题,通过建立新能源电站与SVG 阻抗模型,根据阻抗分析法,分析发现级联H 桥SVG的延时特性导致系统阻抗在高频段呈现负阻尼特性,与交流系统相互作用后引发高频谐振。
在分析含并网变流器谐振问题时,通常采用特征值分析法[4,8]和阻抗分析法[7,10]。其中特征值分析法通过建立系统状态空间方程,分析系统参数与谐振问题的内在关系,但由于特征值分析需要解决多变流器建模时矩阵“维数灾”等问题,在分析系统谐振问题时缺乏优势[1]。因此目前研究中多通过建立变流器阻抗模型后,由阻抗分析法分析系统谐振机理,其优势体现为便于工程分析系统谐振问题、易于测量变流器阻抗等。
现有研究中指出SVG 控制模式、控制参数都会对系统稳定性产生影响,因此针对此类问题,文献[8]提出可以通过优化控制器参数或改变SVG 控制模式实现次同步谐振抑制。文献[11]则是通过优化SVG实现重构系统阻抗特性达到抑制次同步谐振的效果。对于由SVG 引起的高频谐振问题,文献[9]提出对SVG 电压前馈优化实现优化含SVG 的新能源电站系统阻抗特性,以达到抑制高频谐振的效果。
通过对上述文献分析可知,目前对于次同步与高频谐振问题的研究成果已较为丰硕,而对于含SVG的集群风电场中频谐振机理分析和抑制方法的研究还处于初步探索阶段,需要对系统中频谐振现象的本质、诱因以及建模分析方法展开深入讨论。因此本文以含SVG 的风电场区域系统为研究对象,基于谐波线性化理论,建立风电场区域系统序阻抗模型,分析SVG 不同控制模式、控制参数以及空载线路投入对风电场区域系统中频谐振的影响,并提出一种基于SVG 电压前馈施加低通滤波器的中频谐振抑制方法,最后通过电磁仿真验证了理论分析和抑制方法的正确性。
1 风电场区域系统结构与谐振现象
在风资源富集地区,各风电场通常经220 kV 或110 kV 馈线接入汇流站,利用变压器升压将电能送入输电网,其系统结构如附录A 图A1 所示,其中多台直驱风机等效为单台直驱风机[10]。图中:风电场1的直驱风机经0.69 kV/35 kV 变压器与自备SVG 并联于35 kV 母线;风电场2 经馈线2 接入风电场1 的220 kV母线;Z220为线路阻抗。
然而通过对此类风电场的监测和研究发现,随着风电场运行工况的变化,风电场SVG 存在中高频谐振问题[10,12],其中最具代表性的是,新疆哈密地区由于220 kV 汇流站空载线路投入,导致系统内SVG发生频率为2 200 Hz和3 100 Hz的高频谐振现象[13]。这说明在风电密集地区,分析系统谐振问题不仅要考虑风机的运行状态,还要考虑诸如区域电网结构变化、SVG控制模式切换等因素对谐振的影响作用。针对此类问题,本文基于对SVG 与风机的联合序阻抗建模,尝试利用序阻抗分析法,从SVG 控制模式与空载线路投入对系统阻抗影响入手,开展对风电场中频谐振机理和抑制方法的研究。
2 风电场风机与SVG序阻抗建模
2.1 2种控制模式SVG序阻抗建模
级联H 桥SVG 主电路与控制部分如图1 所示。图中:vgt(t=A,B,C)为电网电压;Zg为电网阻抗;L为SVG 滤波电感;iwt为风电场输出电流;θPLL为锁相角;Htn(n=1,2,…,N,其中N为子模块总数)为t相第n个子模块;vdc_tn为t相第n个子模块电容电压。SVG 通过对并网点电压vt和电网电流igt进行采样,计算电网瞬时功率,经过功率外环控制器获得q轴电流参考值iqref,通过对各子模块直流电容电压之和∑nvdc_tn与参考值作差,经过直流外环控制器得到d轴电流参考值idref,将SVG 输出电流it进行dq分解后得到d轴分量id和q轴分量iq,将其分别与idref和iqref作差,经过电流内环得到参考电压d轴分量vmd和q轴分量vmq,最后进行反变换并计及相内直流电压均衡控制提供的Δvmt,为调制提供电压参考指令。

图1 级联H桥SVG主电路与控制框图Fig.1 Main circuit and control block diagram of cascaded H-bridge SVG
本文采用谐波线性化的方法,进行不同控制模式下SVG 的序阻抗建模。考虑到变流器直流外环参数对中高频阻抗影响较弱[11],因此在建模过程中对直流外环做理想等效处理。由图1 可知,并网点电压与SVG阀侧电压关系如附录A式(A1)所示。
假设注入系统正负序小扰动电压[14],此时并网点A相电压、SVG输出A相电流时域表达式分别为:
式中:V1、ω1分别为并网点基波电压幅值与角速度;I1、φi1分别为SVG 输出基波电流幅值与相位;Vp、ωp、φvp分别为并网点正序扰动电压幅值、角速度与相位;Isp、φip分别为SVG 输出正序扰动电流幅值与相位;Vn、ωn、φvn分别为并网点负序扰动电压幅值、角速度与相位;Isn、φin分别为SVG 输出负序扰动电流幅值与相位。并网点电压与SVG 输出电流频域表达式如附录A式(A2)、(A3)所示。
2.1.1 锁相环建模
当电网电压存在谐波扰动时,锁相环会以相位误差的形式将此扰动通过派克变换引入控制器电流内环。同时由于锁相环的存在,变流器稳态工作点变化也会对阻抗产生影响[15],因此在建立变流器序阻抗模型时需对锁相环进行谐波线性化建模。由于已有文献列写了锁相环的谐波线性化推导[14],因此直接给出锁相误差与并网点电压谐波扰动关系表达式,如附录A式(A4)、(A5)所示。
2.1.2 定功率因数控制外环建模
SVG 定功率因数控制模式如图2 所示。定功率因数控制是将并网点电压与电网电流,通过静止坐标瞬时功率计算公式得到电网瞬时有功Pg和电网瞬时无功Qg,利用功率因数λ与Pg获得无功参考值Qgref,并与电网瞬时无功作差,通过比例积分(proportional integral,PI)控制器得到电流内环q轴电流参考值iqref。图中Hq为功率外环PI控制器传递函数。

图2 定功率因数控制模式框图Fig.2 Block diagram of constant power factor control mode
由图2可知:
式中:a=tan(arccosλ)。静止坐标系下瞬时功率计算公式为:
根据静止坐标系下瞬时功率计算公式,得到电网瞬时功率频域表达式为:


根据式(2)—(5),得到iqref的频域表达式为:
式中:Iq0为无功电流参考值直流分量。
由于定功率因数控制引入电网正负序电流扰动分量,本文利用式(7)、(8)将电网电流扰动分量转换为SVG 正负序电流扰动分量与风电场正负序阻抗,由此获得SVG正负序阻抗模型。
将风电场等效为正序阻抗Zp_w和负序阻抗Zn_w,因此风电场正序电流Iwp为:
根据图1 与基尔霍夫电流定律,将电网侧正序电流表示为:
由式(8)可知,电网正序电流可由风电场正序阻抗、并网点正序扰动电压和SVG 正序扰动电流表示(电网负序电流推导步骤相同)。将式(8)代入式(6)中获得iqref的频域表达式为:
2.1.3 恒无功控制外环建模
SVG 恒无功控制模式控制结构见附录B 图B1,将并网点电压与SVG 输出电流采样后,经过静止坐标系下瞬时无功计算公式计算得到SVG 实际发出无功Qsvg,与设定参考值Qref作差后,通过外环PI控制器得到电流内环q轴参考值。
由于恒无功控制外环建模与定功率因数控制建模过程相似,因此直接给出iqref频域表达式如式(10)所示,具体推导过程见附录B式(B1)—(B3)。

电流内环建模的推导过程见附录C。最后将vmd与vmq频域表达式进行派克反变换后得到vmt频域表达式,结合附录A 式(A1)得到SVG 处于定功率因数控制模式时正序阻抗,如附录D式(D1)所示,SVG处于恒无功控制模式时正序阻抗如附录D 式(D2)所示。
2.2 直驱风机序阻抗建模
直驱风机网侧变流器主电路与控制部分结构见附录E 图E1。直流外环通过控制直流电压来实现机侧有功功率与网侧有功功率的平衡,无功外环通过采样风机电流与变压器低压侧电压计算无功与给定无功参考值做差,通过无功外环PI 控制器得到电流内环q轴参考值iqref,并将idref、iqref送入电流内环得到vmd与vmq,进行派克反变换得到参考波,经调制控制实现对网侧变流器输出控制。
如果采用忽略功率外环的简化模型,则可能导致风机变流器中频段阻抗特性表征不准确[16],所以对直驱风机进行阻抗建模时需要考虑无功外环对风机阻抗的影响。由于直流电容容值较大,且直流外环带宽较窄[11],这里认为直流电压恒定,忽略直流外环对风电场区域系统中频谐振的影响。
由于直驱风机网侧变流器控制方式与SVG 恒无功控制方式相同,因此不再给出推导过程,直驱风机变流器正序阻抗Zp_D-PMSG见附录E式(E1)。
考虑已有文献对变压器模型进行推导,因此本文根据文献[17]中变压器模型给出直驱风机折算到高压侧正序阻抗表达式为:
式中:K为变压器变比;ZT为折算到35 kV 侧变压器阻抗;nw为风机数量;Zw为直驱风机折算到高压侧阻抗。
3 风电场区域系统中频谐振机理分析及抑制措施
3.1 风电场区域系统中频谐振机理分析
根据第2 章获得的SVG 与风机序阻抗模型,利用阻抗分析法,得出SVG 采用定功率因数控制模式时投入空载馈线2 后引发风电场区域系统发生中频谐振问题的机理。
当采用阻抗分析法分析稳定性问题时,通常将电网等效为理想电压源与阻抗串联,风机变流器与SVG 进行诺顿等效如附录F 图F1 所示。由图可知,风电场区域系统侧输出电流ig可表示为:

式中:Zl为线路阻抗;Zs为SVG阻抗。
根据式(12)分析Zg(s)/Zo(s)的稳定性即可确定风电场区域系统是否可以稳定运行[14,18]。当电网阻抗与风电场区域系统阻抗交点频率为fc时,交点处相位裕度δPM可以表示为:
结合文献[19]所推导线路阻抗模型,式(11)、(13)、式(D1)、(D2)、式(E1)以及附录F 表F1—F3中提供的系统参数,绘制风电场区域系统阻抗Zo(s)的伯德图如图3 所示,其中电网阻抗Zg为0.016 H,SVG采用定功率因数控制模式。

图3 风电场区域系统阻抗特性Fig.3 Impedance characteristics of wind farm area system
基于式(12)、(14),根据并网逆变系统阻抗分析奈奎斯特稳定判据,辨析幅频阻抗交点处相位裕度性质,即可判定系统阻尼特性以及是否存在谐振风险。分析图3可知,空载馈线2投入前风电场区域系统与电网阻抗交点为272 Hz,交点处相位裕度为正(2°),风电场区域系统不会发生谐振现象,但是当空载馈线2 投入后,电网阻抗与风电场区域系统阻抗交点为264 Hz,根据式(14)可知交点处相位裕度为负(-4°),风电场区域系统在264 Hz附近表现为负阻尼特性,存在谐振风险。
3.2 SVG对风电场区域系统谐振的影响分析
3.2.1 SVG控制模式对风电场系统稳定性的影响
SVG 的主要控制模式包括定电压控制、定功率因数控制和恒无功控制,为满足无功补偿容量要求,风电场区域汇流站内通常配置多台SVG,考虑到定电压控制模式容易引发SVG 多机谐振失稳[20],且已有学者对定电压控制模式下SVG 系统稳定性问题进行过深入分析,因此本文重点对SVG 采用定功率因数控制和恒无功控制下的风电场系统整体稳定问题进行对比研究。
根据3.1 节阻抗分析方法,绘制SVG 采用定功率因数控制模式与恒无功控制模式下风电场区域系统阻抗特性曲线,如图4所示。

图4 SVG的2种控制模式对风电场区域系统阻抗特性的影响Fig.4 Influence of two control modes of SVG on system impedance characteristics of wind farm area system
分析图4 可知:投入馈线2 后,SVG 采用定功率因数控制时,含SVG 风电场区域与电网的阻抗交点频率为264 Hz;SVG 采用恒无功控制模式时,阻抗交点对应频率为257 Hz,风电场区域系统阻抗幅值在该频段无明显变化。对比相频特性发现,与恒无功控制模式相比,SVG 采用定功率因数控制时系统负阻尼区由131 Hz 增大至276 Hz,风电场区域系统在中频段谐振发生概率升高。
3.2.2 SVG控制参数对风电场系统稳定性的影响
通过对不同控制模式分析发现,当SVG 处于定功率因数控制模式时更容易引发风电场系统谐振。本节重点分析定功率因数控制模式下SVG 内外环比例系数变化对风电场区域系统阻抗特性的影响规律,不同比例系数对应系统阻抗变化趋势分别如附录G 图G1、G2所示。由图G1可知,随着功率外环比例系数增大,风电场区域系统负阻尼区域增大。图G2 表明,电流内环比例系数对风电场区域系统阻抗特性的影响与无功外环比例系数类似。上述分析说明,设计SVG 控制器内外环系数时,应注意比例系数对系统稳定性的影响,尤其是处于定功率因数控制模式时,功率外环比例系数对风电场区域系统稳定性影响。
3.2.3 SVG电压前馈对风电场系统稳定性的影响
将电网电压前馈加入控制环路,可以降低电网电压畸变导致的变流器输出电流畸变,减小变流器启动过程中的冲击电流。然而弱电网中,直接引入电压前馈可能会对变流器稳定性产生影响,需要通过前馈优化来改善系统稳定性[21]。
包含电网电压比例前馈的SVG 控制系统阻抗特性如附录G 图G3所示。由图可知:将电网电压全部前馈到控制环路后,系统在中频段出现了负阻尼区域,容易引发谐振现象;而将前馈系数减小后,风电场区域系统阻抗相位裕度明显增大,理论上降低了谐振产生的风险。通过改变SVG 电压前馈系数后发现,电压前馈相较于SVG 内外环参数对风电场区域系统阻抗特性影响更为明显。
3.3 风电场区域系统谐振抑制措施
通过3.2 节分析可知,在定功率因数控制模式下,虽然改变内外环控制系数可使风电场系统整体阻抗发生变化,但改变内外环系数以及电压前馈系数,将影响正常工况下变流器的动态响应速度等性能[21],因此并不适用于系统谐振抑制。目前,有学者利用在控制器电压前馈中加入滤波器的方法解决模块化多电平换流器出现的高频谐振问题[22],核心思想是利用滤波器屏蔽电压前馈引入的谐波扰动,切断系统谐波传递路径,该方法的优点在于不改变控制器内外环参数,保留了正常工况下换流器的原有工作特性。鉴于上述分析,本节尝试将二阶低通滤波器应用于SVG 电压前馈环节,设置图C1中前馈函数Kf为二阶低通滤波器即可实现SVG 阻抗重塑,通过对SVG 的阻抗重塑消除风电场系统在中频段的负阻尼区域,最终实现风电场区域系统中频谐振的抑制。二阶低通滤波器传递函数表示为:
式中:ωn=2πfn,fn为截止频率;ξ为二阶低通滤波器阻尼系数,ξ=0.707。
根据式(13)并结合式(15)绘制fn为100、200、300 Hz 对应风电场区域系统阻抗曲线,如附录G 图G4 所示。由图可知,随着fn的增大,风电场区域系统相位裕度下降,在相同阻尼比的情况下采用fn=100 Hz 系统能够获得较大的相位裕度,但截止频率太小可能影响系统故障穿越等特性,因此采用fn=200 Hz。
根据所提谐振抑制措施,绘制风电场区域系统阻抗特性曲线如图5所示。分析图5发现,采用谐振抑制措施前、后风电场系统与电网阻抗交点基本未发生变化,但是交点处相位裕度由-4°提升到40°,理论上降低了系统发生谐振的风险。
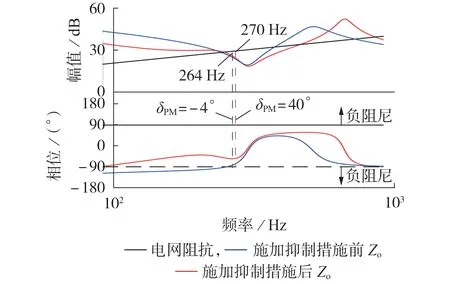
图5 施加谐振抑制措施前、后风电场区域系统阻抗特性Fig.5 Impedance characteristics of wind farm area system before and after applying resonance suppression measures
4 仿真验证及分析
基于RT-LAB 5600 仿真平台,根据图A1 所示风电场区域系统结构和表F1 —F3 中系统参数,搭建风电场区域系统仿真模型,验证第2 章获得的序阻抗模型、第3 章风电场区域系统中频谐振机理分析的正确性以及所提谐振抑制措施的有效性。
4.1 理论阻抗模型验证
为验证SVG 与直驱风机序阻抗建模的正确性,利用已搭建的系统仿真模型,进行扫频验证。
SVG、直驱风机和风电场区域系统理论建模与扫频获得的阻抗伯德图分别如附录H 图H1 —H3所示。由图可知,扫频结果与第2 章获得的理论阻抗结果基本吻合,验证了理论阻抗建模的正确性。
4.2 风电场区域系统中频谐振机理分析验证
基于风电场区域系统仿真模型,进行2 种工况仿真:①工况1,[3.5,4.5]s 时SVG 采用定功率因数控制模式,4 s 之前稳定运行,4 s 时投入空载馈线2,4.5 s 后SVG 切换为恒无功控制模式;②工况2,与工况1 区别在于[3.5,5]s时SVG 采用定功率因数控制模式,4.5 s后投入谐振抑制措施。
控制模式切换下的仿真波形如图6 所示。分析图6 可知,SVG 采用定功率因数控制模式,投入空载馈线2 后,风电场区域系统发生谐振,风电场1 中35 kV 母线电压和电流出现谐波畸变;4.5 s 时SVG切换为恒无功控制模式,系统谐振现象消失,电压和电流恢复正常。

图6 控制模式切换下的仿真波形Fig.6 Simulative waveforms during control mode switching
进一步对谐振过程中35 kV 母线电压和电流进行傅里叶分析,结果如图7 所示。观察图7 可以发现,谐振时谐振频率约为270 Hz,与3.1 节理论分析风电场区域系统谐振频率264 Hz基本吻合。

图7 谐振过程中35 kV母线电压与电流傅里叶分析Fig.7 Fourier analysis of 35 kV bus voltage and current during resonance process
当SVG 切换为恒无功控制模式时,35 kV 母线电压与电流傅里叶分析如附录H 图H4 所示。由图可知:35 kV 母线电压的总谐波畸变率ξvTHD由10.19 % 减小为0.26 %,电流的总谐波畸变率ξiTHD由124.83 % 减小为3.32 %,这与3.2.1 节中定功率因数控制相较于恒无功控制模式扩大了负阻尼区间,发生中频谐振风险更高的结论吻合,进一步证明,某些特定工况条件下SVG 控制模式与系统谐振存在内在关联。
4.3 中频谐振抑制效果验证
施加谐振抑制措施前、后仿真波形如附录H 图H5 所示。由图可知,定功率因数控制模式下,4.5 s时SVG 启用基于前馈滤波器的谐振抑制措施,由于空载馈线2 投入导致的系统谐振现象得到了明显抑制,这与3.3节中理论分析一致。进一步对启用谐振抑制措施后的35 kV 母线电压与电网电流进行傅里叶分析,结果如附录H 图H6 所示。比较图7 和图H6,发现启用谐振抑制措施后,35 kV 母线电压的总谐波畸变率ξvTHD由10.19%减小为0.14%,35 kV母线电流的总谐波畸变率ξiTHD由124.83 % 减小为1.47 %,谐振抑制效果优于恒无功控制模式,从而验证了本文所提谐振抑制措施的有效性。
5 结论
本文通过对含SVG 的直驱风电场进行序阻抗建模,研究风电场系统运行稳定性与SVG 控制模式间的内在关系,并提出一种基于电压前馈改进的SVG 控制措施优化方法,以实现对SVG 及风电场并联系统中频谐振的抑制,具体结论如下:
1)通过对SVG 不同控制模式进行建模分析发现,相比于恒无功控制模式,当SVG 采用定功率因数控制模式时,风电场区域系统负阻尼区间明显扩大,可能导致系统发生中频谐振的概率升高;
2)SVG 无功外环和电流内环比例系数取值直接影响风电场区域系统阻抗特性,随着二者比例系数的增大,含SVG 的风电场区域系统阻抗可能在中频区域由正阻尼特性转变为负阻尼特性,因此SVG 对应控制参数设计需考虑其取值范围,以降低由此引发的风电场系统谐振风险;
3)在SVG 采用定功率因数控制条件下,单纯依靠减小其无功外环与电流内环的比例系数,并不能完全消除系统中频段出现的负阻尼区,而优化SVG电压前馈环节可实现系统阻抗重塑,以提高风电场区域系统阻抗相位裕度,进而消除负阻尼,实现对风电场区域系统谐振的有效抑制。
附录见本刊网络版(http://www.epae.cn)。

