云计算环境下大数据的大规模任务处理研究
李德刚,王成威,于 振,李广义,王烁寰
(山东省国际信托股份有限公司,山东 济南 250101)
0 引 言
随着信息技术的飞速发展和大数据应用的普及,人们进入了信息时代[1]。大数据的持续增长和多样化的数据类型,给传统的任务处理与数据分析带来了前所未有的挑战。在高度数字化和信息化的时代背景下,云计算作为一种强大的计算和存储平台,成为解决大规模任务处理问题的重要方式[2]。然而,随着数据规模的急剧扩大,传统的任务处理方法面临着问题日益复杂的情况[3]。如何高效处理海量的数据任务,是云计算和分布式系统的热门议题。此外,不同领域和资源之间的异构性,以及多个领域之间的数据通信需求,使任务处理和资源优化更加复杂[4]。在云计算环境中,各个域之间的资源分布和性能差异可能导致任务分配不均和资源利用率低下等问题出现。为有效应对这些挑战,研究者们积极探索任务处理方法,以实现任务的智能分配、资源的高效利用以及整体系统性能的提升。实际应用场景中,大规模任务处理的效率和质量会直接影响系统的性能与用户体验。然而,传统单一领域任务处理方法经常忽视资源的异质性和多领域之间的通信成本,难以满足多样化需求[5]。随着任务规模的不断膨胀,如何合理分配任务,同时保持每个节点的负载平衡,并减少数据传输成本,变得愈发复杂。为解决这些问题,文章提出一种基于多目标粒子群算法的创新性方法,目的是在大规模任务处理过程中实现任务负载的均衡和域间通信带宽资源成本的最小化。通过融合帕累托支配理论、拥挤度比较法以及柯西变异操作,所提方法在解决任务分配和资源优化方面取得了显著成果,有助于为大数据环境下的多领域任务处理提供指导,推动该领域的进一步发展,以应对日益复杂和庞大的任务处理挑战,同时为云计算在大规模任务处理中的应用提供新的思路和方法。
1 系统架构设计
文章提出一种基于多域并行计算思想的大规模任务处理方法。每个域内的节点处理速度受计算资源性能和内部调度策略的影响。一方面,传统方法通常将数据处理任务按照某种规则分配到各个域的节点,易导致部分节点负载过重,资源利用不均,产生资源浪费问题[6,7]。因此,设计一种能够高效合理实现数据中心负载均衡的大规模任务处理方法显得尤为重要[8]。另一方面,云计算环境下的大规模任务处理由于域间数据传输量大,给固定网络资源带来了巨大压力,导致带宽资源成本急剧上升[9]。多域环境下的大规模任务部署实例如图1 所示。
针对处理大规模任务面临的挑战,基于云计算环境的大规模任务处理方法能够提供关键性的解决方案。通过创新性地应用多域并行计算思想、帕累托支配理论、拥挤度比较法以及柯西变异操作等,设计了一种高效快速的任务处理方法,可实现数据中心负载均衡和带宽资源成本的优化,有助于提高大数据分析和处理效率,实现长期收益[10]。
大数据环境下基于多域的大规模任务处理方法的逻辑架构如图2 所示。文章构建基于多域的大规模任务处理方法的系统架构,在大数据环境下实现任务处理的高效性和资源优化。该方法的逻辑架构清晰展现了各个模块之间的紧密协作,确保大规模任务能够得到有效处理。在整个处理流程中,不同模块之间的密切协作是实现任务高效处理的关键。监控器模块通过获取信息,为系统提供重要的输入数据,包括大规模任务请求的资源需求信息、可用物理节点以及链路的资源状态等。这些数据为后续的虚拟网络映射方案奠定了基础。虚拟网络映射控制器模块负责执行虚拟节点映射操作,生成虚拟网络映射方案,并根据实际情况进行调整。部署控制器模块承担了任务部署的重要任务,根据虚拟网络映射方案、节点以及链路资源状态,制定任务部署策略,实现任务的合理分配和节点的负载均衡。
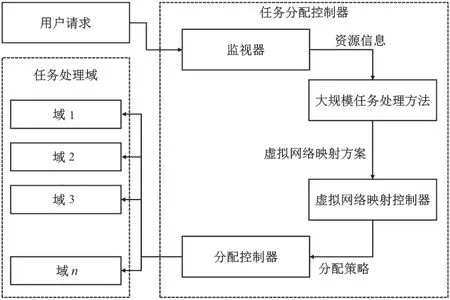
图2 大数据环境下基于多域的大规模任务处理方法的逻辑架构
这些模块协同作用,使得整个系统能够高效处理大规模任务。通过监控器的信息获取和虚拟网络映射控制器的执行,能够在任务映射过程中保持负载均衡,并最小化带宽资源成本。部署控制器的任务策略进一步优化了任务的部署过程,确保任务能够得到有效执行。通过协同工作,基于多域的大规模任务处理方法实现了大规模任务的高效处理和资源优化。图2 的系统架构提供了一个直观视角,有助于更好地理解该方法的工作流程和各模块之间的相互关系,对于推动大规模任务处理领域的研究和应用具有积极意义。该方法可以更好地应对大数据环境下任务处理的挑战,提高任务处理的效率和质量。
2 实现过程
通过将多域结构应用于大规模任务处理领域,构建了一种基于多域协作的系统架构,同时基于帕累托理论方法,在多域协作的背景下优化大规模任务处理流程,为解决大规模任务处理问题提供了更加高效的解决方案。
与传统的单目标粒子群算法不同,所提的大规模任务处理方法采用一种全新的初始种群生成策略。一方面,在算法迭代过程中运用帕累托支配理论,可以比较可行解之间的关系,通过使用快速非支配选择方法,可以获得帕累托最优解集,从而获取映射方案的最优解集。另一方面,采用拥挤度比较法,设计了一个选取问题最终唯一解的策略,以确保粒子群的多样性。
第一步,设定最大迭代次数为Max Generation,并初始化每个粒子的位置向量Pop[i],同时将每个粒子的速度向量设置为0。在每次迭代过程中,运用Kruskal 最小生成树算法,从可用物理路径集合中动态选择权重最小的物理路径,评估种群中的每个粒子,计算其适应度值。
第二步,求解帕累托最优解集,获得最优的虚拟网络映射方案集合。
第三步,引入拥挤度比较法,获得唯一的最优解。拥挤度比较法需要根据欧几里得距离公式,计算围绕每个可行解形成的最小矩形的对角线长度,将其定义为变量Di,作为拥挤度的度量。可行解拥挤程度的计算如图3 所示,基于可行解所在的最小矩形的对角线长度,可以求得可行解的拥挤度。
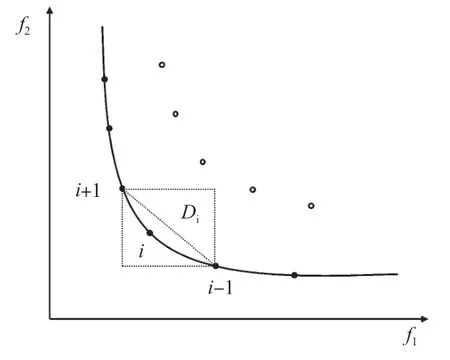
图3 可行解拥挤程度的计算
第四步,将具有个体极值的历史最优位置向量进行存档。进化过程中,算法会将每个粒子的当前位置向量设置为其个体历史最佳位置向量pbest,并将每个粒子的当前适应度值设置为其个体极值。
第五步,通过循环操作搜索最优解。
首先,更新每个粒子的速度,即
式中:w为惯性权重;Vel[i]和Pop[i]分别为第i个粒子的速度向量和位置向量;r1和r2为学习因子,取值为0 ~1;pbest[i]为个体历史最优位置向量。
其次,引入柯西变异方法,计算种群中第j维粒子的平均速度,计算公式为
式中:Velij为第i个粒子在第j维上的速度,而AvgVelj∈[-AvgVelmax,AvgVelmax],将AvgVelmax设为1;PopScale为粒子种群的大小。
最后,对全局最优位置向量gbest采取变异措施。经过变异后得到可行解gmutbest,其计算公式为
式中:F为随机数;[Popmin,Popmax]为问题的定义域。通过比较和全局最优位置向量gbest,选择更优解进行存档更新,然后进行迭代,直至达到最大迭代次数。
3 结 论
文章提出一种应用于大数据环境下多域大规模任务处理的启发式方法。首先,引入一种创新性方法迅速获取虚拟网络映射方案的最优解集,即算法过程中的帕累托最优解集。通过应用帕累托支配理论,在保持最大映射成功率的前提下,获得一系列高质量的虚拟网络映射方案。其次,设计并采用拥挤度比较法,从帕累托最优解集中选取最终的唯一解,不仅能够确保算法的种群多样性,还能够在保持高质量解的基础上提升算法性能。最后,为避免陷入局部最优,引入柯西变异操作,以增强算法的全局搜索性能,确保能够在迭代过程中发现更优解,从而得到最终的唯一最优解,即最优虚拟网络映射方案。

