电力低压系统线损分析与优化研究
李 想
(国网江苏省电力有限公司南京供电分公司,江苏 南京 210000)
0 引 言
随着国民经济的快速发展,社会对于电力的需求也越来越多。为进一步提升人们的生活质量,国家提出进一步对电力系统进行改革[1-4]。但是,目前的电力供给难以匹配经济的高速发展,许多地区不可避免地出现了电力供给不足的难题[5-7]。分析各级电力网的损耗可以发现,10 kV 以下的电能损耗较高,因此许多研究者开始注重研究线损的降低和优化问题。针对该问题,文章探讨分析了2 种经典的低压线损计算方法,并基于遗传算法对2 种方法进行优化,旨在进一步降低低压配电系统的线损。
1 常见的低压配电网线损计算方法
目前,在计算低压配电网的线损时,通常是按照台区划分进行计算。低压的线损理论可以参照中压的线损理论基础,如均方根电流法和台区损失率法等,但是该类方法会产生较大计算误差,使得计算出的线损值低于实际值。基于该背景,介绍2 中常用的小误差低压配电网线损计算方法。
1.1 等值电阻法
以0.4 kV 低压配电网为例,其线损的计算公式为
式中:ΔA表示损失电量值;N表示电力网络的结构系数;k表示负荷电流曲线的形状系数;Ipj表示被计算的j线路首段的平均电流值;Req表示等值电阻;T表示供电时间。
其中,根据供电形式的不同,结构系数N的数值也随之变化,如线路结构分别为单相2 线、三相3线和三相4 线时,N的值分别为2、3、3.5。
1.2 前推回代潮流法
基于已知的始端节点电压和末端负荷功率,可以得到配电网络中其他节点的电压初始值。以馈线为基本计算单位,基于负荷功率,从线路末端向始端进行回代推导,经过前推过程,可以得到所有元件的损耗功率大小。通过回代,可以逐个计算从线路始端到末端的每个节点的压降,即节点电压。对网络的节点支路进行全面搜索,基于电力网络中各个节点的支路矩阵,可以分别得到支路、节点层次、首节点以及末节点的矩阵,同时可以得到其他关联矩阵。
研究者基于配电网的树状特点提出了前推回代潮流法,其原理是基尔霍夫定律,首先计算节点电流,其次计算支路电流,最后计算节点线损与节点电压。
本研究的网络重构环节中,主要基于等值电阻法和前推回代潮流法计算线损。将线损函数作为目标函数,以该函数为优化目标,利用遗传算法优化线损,并基于算例分析对比优化效果。
2 网络重构的数学模型
2.1 确定目标函数
基于改进的遗传算法,优化由等值电阻法和前推回代潮流法计算得到的电网线损,将电网线损作为优化算法的优化目标。
等值电阻法的目标函数公式为
式中:F1表示等值电阻法的目标函数;Ploss表示网络的损耗;b表示支路序号;kb表示支路b的开关情况,一般取0 或1;Nb表示网络支路的总和。
前推回代潮流法的目标函数公式为
式中:F2表示前推回代潮流法的目标函数;Ib表示支路b的电流值;rb表示支路b的电阻值。
2.2 确定约束条件
(1)网络结构约束。网络结构需要满足辐射形状,即供电电源和负荷需要对应。
(2)电流和电压的约束。其约束条件的公式为
式中:Ib表示支路b的电流,b的取值范围是[1,m],m为支路总数;Uimin表示i节点电压的下限、Uimax表示i节点电压的上限;Ui表示节点i的电压,i的取值范围为[1,n],n为节点总数。
(3)线路容量约束。该约束也可以表述为重构后的网络没有过负荷现象,其约束条件的公式为
式中:Sb表示支路b的实际传输功率,b=1, 2,…,m;Sbmax表示支路b最大的传输功率值。
2.3 改进的遗传算法
经典遗传算法会出现提早收敛的问题,针对该问题,自适应遗传算法可以进行解决。经典遗传算法为了保持种群的多样性,选择在全局范围内进行搜索。搜索过程的结尾阶段,算法结果已经与最优解十分接近,因此需要转换成小范围搜索。而决定遗传算法收敛性的操作一般在算法的交叉阶段和变异阶段,因此,本研究选择对这2 个阶段进行改进,改进方案如下。
(1)自适应遗传算法能够使交叉与变异的概率随着迭代次数的变化而变化。如果染色体适应度较高,那么就让其尽可能保持不交叉的状态,从而提高变异概率。适应度的高低是相对于平均适应度而言,该操作可以使得种群里的优良个体保留了下来,避免早熟问题。
(2)提出精英保留方略,无论进行交叉操作还是变异操作,操作前后都需要比较个体的适应度,采用其中较高适应度的操作方式。该方略可以尽可能地保留优良个体,提升优化速度。
2.3.1 自适应交叉算子
为增强算法的搜索能力,交叉概率需要随着适应度值不断变化。交叉概率的计算公式为
式中:Pcmax表示最大交叉概率;Pcmin表示最小交叉概率;Mmax表示算法指定的最优个体的最少代数;m表示最优个体已经保持的代数;Pcm表示m代最优个体保留的交叉概率。
2.3.2 变异算子
随着遗传代数的变化,变异率呈现指数下降趋势。因此,本研究采用的变异操作的公式为
式中:Pmmax表示最大交叉概率;Pmmin表示最小交叉概率;M表示算法指定的最优个体的最少代数;m表示最优个体已经保持的代数;Pmm表示m代的最优个体保留的交叉概率。
2.3.3 总体流程
基于改进遗传算法的线损优化流程如图1 所示。具体步骤如下:首先,分析某个具体问题,然后求出所分析问题的参数,确定相应的目标函数和编码方案;其次,基于确定的编码方案生成随机种群;再次,基于当前种群中的个体所对应的网络结构计算线损;最后,判断目标函数是否满足线损限制要求,如果符合就跳出判断,否则就改进遗传算法优化,生成新的网络结构,计算线损直至线损满足要求。
3 算例分析
馈线16 节点配电网络如图2 所示。以图2 为例,经过详细的推导,可以确定电压的额定值为23 kV,总有功功率为28.7 MW,总无功功率为17.3 Mvar,基准电压和基准功率分别为10 kV 和100 MVA。
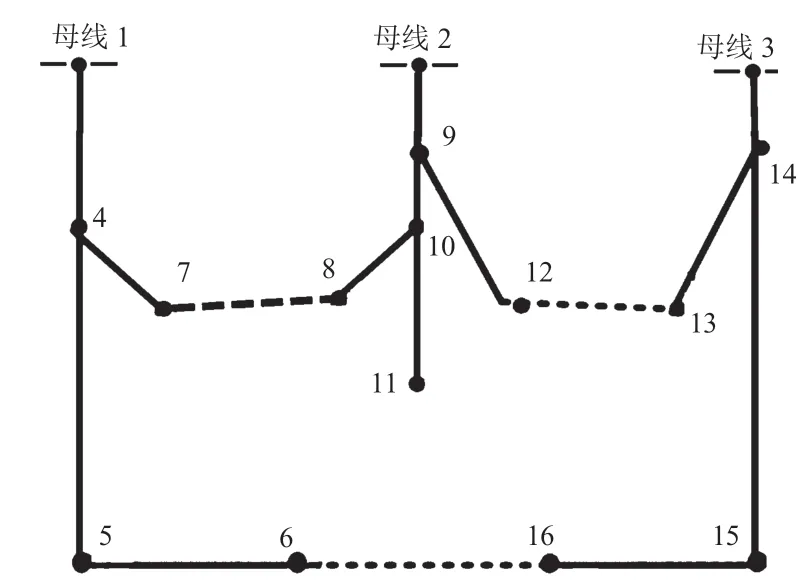
图2 馈线16 节点配电网络
基于改进的遗传算法,采用等值电阻法计算线损的线损变化如图3 所示,采用前推回代潮流法计算线损的线损变化如图4 所示。

图3 等值电阻法计算线损的线损变化
从图3 和图4 中可以看出,随着迭代次数的增多,线损在不断地减少。基于改进的遗传算法,前推回代潮流法的网络重构和等值电阻法的网络重构分别在40 代和80 代左右收敛,前者收敛速度远大于后者的收敛速度。此外,采用前推回代潮流法的网络重构前的损耗要比网络重构后的损耗多66.92 kW,降低了10.84%的线损率;采用等值电阻法的在网络重构前的损耗要比网络重构后的损耗多42.32 kW,降低了6.91%的线损率。
经过实验仿真可以得到,基于2 种方法对网络进行重构,都可以降低配电网络的损耗。但是,前推回代潮流法比等值电阻法降低的线损更多,收敛速度更快。
4 结 论
目前,国民经济正在飞快增长,人们对于电力的需求越来越高。因此,相关部门和许多研究者开始着重研究低压系统线损的降低问题。本研究介绍了2种经典的低压线损的计算方法,并基于遗传算法对2种方法进行优化。通过仿真证明2 种方法都可以有效降低线损,并且利用基于改进的遗传算法的前推回代的潮流法进行网络重构,具有更高的降损效率和更快的收敛速度。

