甚高通量卫星通信系统多播场景线性预编码算法

魏强 廖瑛 辛宁 张千 郝媛媛 任术波 缪中宇

(1 国防科技大学 空天科学学院,长沙 410073)(2 中国空间技术研究院通信与导航卫星总体部,北京 100094)

随着高速互联网业务的不断发展,地球同步轨道(GEO)宽带通信卫星系统从C频段、Ku频段宽波束向Ku频段、Ka频段点波束的高通量卫星发展,系统容量大幅提升,真正实现了互联网高速接入[1-2]。高通量卫星最早是由美国航天咨询公司提出的概念,将其定义为“采用多点波束和频率复用技术、在相同频率资源条件下整星容量大幅提升,达到传统固定通信卫星的数倍、面向消费者互联网接入等宽带应用”的卫星。目前,高通量卫星已经成为卫星通信领域的热点之一,包括中国在内的多个国家和地区已成功发射多颗高通量卫星,其中以中星26号卫星为代表的Ka频段高通量卫星整星容量已超过百吉比特每秒[3]。

为进一步提升系统容量,下一代甚高通量卫星(VHTS)通信系统将采用更窄的波束、更高的频率复用程度,但也更容易受到同频干扰等影响。在全频率复用的VHTS通信场景中,线性预编码技术是一种很有潜力的干扰抑制技术[4-5]。针对基于帧的多播线性预编码问题,文献[6]中先通过半阵定放松法(SDR)和高斯随机化获取解耦的服务质量(QoS)问题的解,然后采用次梯度投影法进行功率再分配,二者交替优化直到问题收敛;相比于4色复用的方法和加权公平性算法,该线性预编码技术可以显著提升波束的平均吞吐量,但随着波束内用户数量的增加,每个波束的吞吐量会明显下降。而且,上述线性预编码的计算方法具有较高的复杂度。文献[7]中提出一种中心化的方法,该方法通过连续凸近似的方式将原来非凸问题近似为迭代的二阶锥规划问题。文献[8]中设计了一种基于和速率最大化的线性预编码器,通过分布式的线性接收机将和速率最大化问题转化成加权最小均方误差最小化(WMMSE)问题,然后计算最小均方误差(MMSE)接收机和加权值,进而通过迭代方式求解线性预编码矢量。相比直接采用MMSE线性预编码,该算法的吞吐量性能有显著增加。然而,文献[6-8]中均未考虑数字视频广播第2代扩展标准(DVB-S2X)中多播帧[9]的特点,部分算法的复杂度较高,不适用于VHTS通信系统。

由于前向信号是由信关站发射,且信关站更易获取所有用户的信道状态信息,在前向链路进行预编码设计更便于实际应用。因此,本文针对VHTS通信系统的前向链路,考虑星上功率约束,以最大化系统总吞吐量为目标,设计通信系统多播场景下的线性预编码算法。考虑该优化问题的非凸性,将问题转化成总的最差最小均方误差(MSE)最小化问题,然后利用交替方向乘子法(ADMM)将其分解成多个并行子问题进行求解。仿真结果表明:在用户分组尺寸较大时,本文算法相比于应用MMSE的算法具有显著的吞吐量增益,且其计算复杂度较低。

1 系统模型

1.1 信道模型

VHTS通信系统工作在GEO,其信道受自由空间损耗、波束增益模式及其他附加损耗的影响。对于工作在10GHz以上的卫星信道,雨衰是对流层中大气衰减的主要因素。

(1)自由空间损耗。自由空间损耗是指由于无线电波在空间传播,电波能量随着传播距离增加而损耗,一般采用自由空间损耗系数来表征这种衰减,第i个波束的自由空间损耗系数可以表示为bmax(i)=[c/(4πf)]2/di2,其中,c为光速,f为频率,di为卫星到第i个波束中心的距离。

(2)波束增益。影响信道质量的因素除了自由空间损耗,还有波束增益。在每个波束覆盖区域内,处于中心点的用户终端获得的波束增益最大,其余位置的增益随着与波束中心距离的增大而衰减,用户的接收波束增益具体计算公式可参考文献[10]。

(3)雨衰。由于天气等气象条件的影响,星地链路的信道质量还会受到一些附加的损耗影响,例如降雨导致的雨衰、大气吸收损耗及电离层闪烁。对于10GHz以上的频段,降雨导致的衰减更加严重,而本文采用的是Ka频段,所以在信道建模时需要考虑雨衰对于信道质量的影响。根据国际电信联盟无线电通信组(ITU-R)建议P.1853[11],定义雨衰系数矢量Ψik=[ψ1,ikψ2,ik…ψG,ik]T,那么第i个波束内第k个用户的信道矢量可以表示为

(1)

式中:⊙为哈达玛积;GT,GR分别为发送和接收的天线增益;κTB为噪声功率,其中,κ为玻尔兹曼常数,T为接收机噪声温度,B为载波带宽,为了便于计算,将噪声功率归一化到信道中计算;波束增益矢量bik=[b1,ikb2,ik…bG,ik]T;信道相位分量Φik=[φ1,ikφ2,ik…φG,ik]T,在[0,2π]服从均匀分布。

1.2 信号模型

第i个波束内第k个用户的接收信号可以表示为

(2)

式中:l为除了i以外的波束;nik为噪声。

基于DVB-S2X多播帧的特点,假设si为第i个波束的K个用户数据所组成的数据帧信号,不同波束的信号相互独立,且与噪声nik独立,wi为第i个波束的线性预编码矢量,则第i个波束内第k个用户的信干噪比(SINR)为

(3)

2 线性预编码算法

2.1 和吞吐量最大化问题建立

本文研究的多播场景下线性预编码以最大化系统总吞吐量为目标,并考虑星上功率约束。由于在该场景下每个波束内的数据构成一帧,每个波束的吞吐量由最差的用户SINR决定,根据香农公式,最大化系统的总吞吐量就需要增大每个波束内最差用户的SINR,因此,在考虑星上功率约束的情况下,多播场景下的线性预编码优化问题表示为

(4)

从式(4)可以看出:该问题是一个非凸优化问题,需要将其转化成凸优化问题来求解。文献[8]中证明了和速率最大化问题可以转换成WMMSE问题求解,而优化问题(4)与和速率最大化问题具有相似的结构,因此该问题也可以转换成与WMMSE问题类似的问题求解,即

(5)

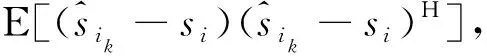
现在通过求解优化问题(5)来得到优化问题(4)的解。对于问题(5),可以看到问题中的优化变量有uik,wi,ti,采用迭代优化的方式求解。

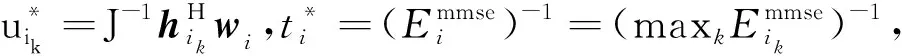
(2)固定变量uik,ti,优化线性预编码矢量wi,得到优化问题。

(6)

2.2 应用ADMM的线性预编码设计

定义αi=maxEik(k∈),且引入3组辅助变量vi=wi,那么优化问题(6)可等价表示为

(7)

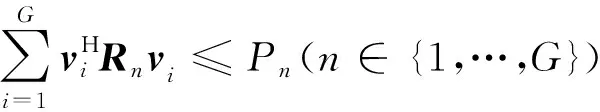
(8)

其拉格朗日形式为

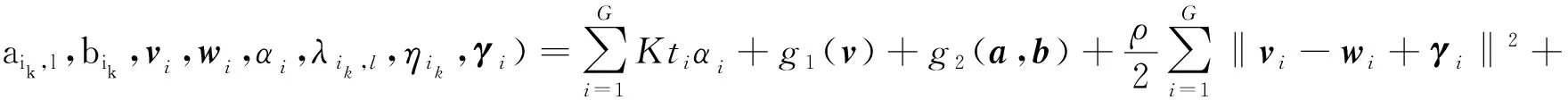
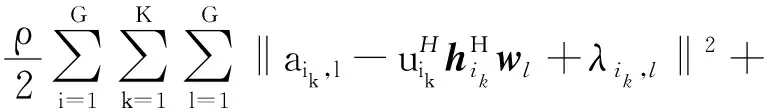
(9)

式中:惩罚参数ρ>0;λ定义为{λik,l|i,l∈{1,…,G},k∈{1,…,K}},η定义为{ηik|i∈{1,…,G},k∈{1,…,K}},γ定义为{γi∈CG|i∈{1,…,G}},分别表示式(9)中各个变量的缩放对偶变量。

分析式(9),可以将变量分成2组,即局部变量{v,a,b}和全局变量{w,α};同样地,目标函数也可以分解,因此采用ADMM的算法来求解式(7),通过交替更新的方式对2组变量进行更新。

2.3 ADMM的变量更新

本节对各组变量的更新进行详细的分析。

2.3.1 更新局部变量{v,a,b}

(10)

(11)

1)更新局部变量{v}

优化问题(10)可以等价为G个并行的子问题求解,每个子问题表示为

(12)

式中:vn,i,wn,i,γn,i分别为vi,wi,γi的第n个元素。

(13)

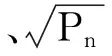
(14)

2)更新局部变量{a,b}

将优化问题(11)分解成GK个子问题并行求解,每个子问题表示为

(15)

其拉格朗日形式为

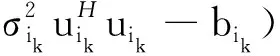
(16)

式中:对偶变量πik≥0。

用最优化理论中KKT条件求解优化问题(16),得到最优解为

(17)

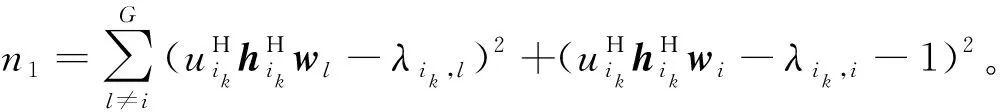
2.3.2 更新全局变量{w,α}

同样,更新全局变量可以分解成2个优化问题,即

(18)

(19)

先求解优化问题(18),该优化问题同样可以分解成G个并行子问题,每个子问题表示为

‖vl-wl+γl‖2

(20)

得到最优的线性预编码矢量为

(21)

再求解优化问题(19),该问题同样可以分解成G个并行的子问题,求得最优解为

(22)

2.3.3 更新对偶变量{λ,η,γ}

对偶变量采用次优梯度法进行更新,即

(23)

式中:迭代幅度值sj=1/j。

经过有限次迭代更新后,ADMM可以获得最优的预编码矢量,然后代入到式(6)中,更新MMSE接收机和加权值,重复该步骤,直到算法收敛。算法的主要实现流程如图2所示。

2.4 算法复杂度分析

文献[12]中已证明对偶变量求解的计算复杂度为对偶问题维度的多项式函数,并可利用次优梯度法在有限次迭代后达到收敛。此外,观察上述算法步骤可知,在每次迭代过程中可通过闭式表达式(14),(17),(21),(22)得到最优解。因此,可以证明本文算法为多项式级计算复杂度并保证收敛。

3 仿真结果与分析

本节提出在VHTS多播场景下将和吞吐量最大化问题转换为加权均方误差最小化问题(以下称为本文算法)求解,在本节对本文算法进行性能仿真并与文献[8]中的应用MMSE的算法进行性能对比分析,两者的计算复杂度均为多项式级复杂度。为保证仿真结果的准确性,2种算法均在同一个场景下进行仿真比较,具体参数如表1所示。

波束的吞吐量是算法性能的重要指标之一,2种算法的性能分别如图3和图4所示。图3表示每帧内调度用户数K为6时2种算法的波束吞吐量,图4表示每帧内调度的用户数K不同时2种算法的平均每个波束的吞吐量。

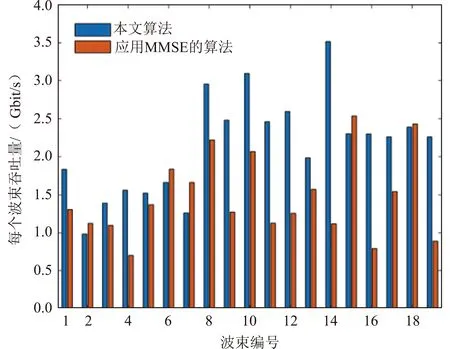
图3 K为6时每个波束的吞吐量Fig.3 Throughput of each beam for K=6

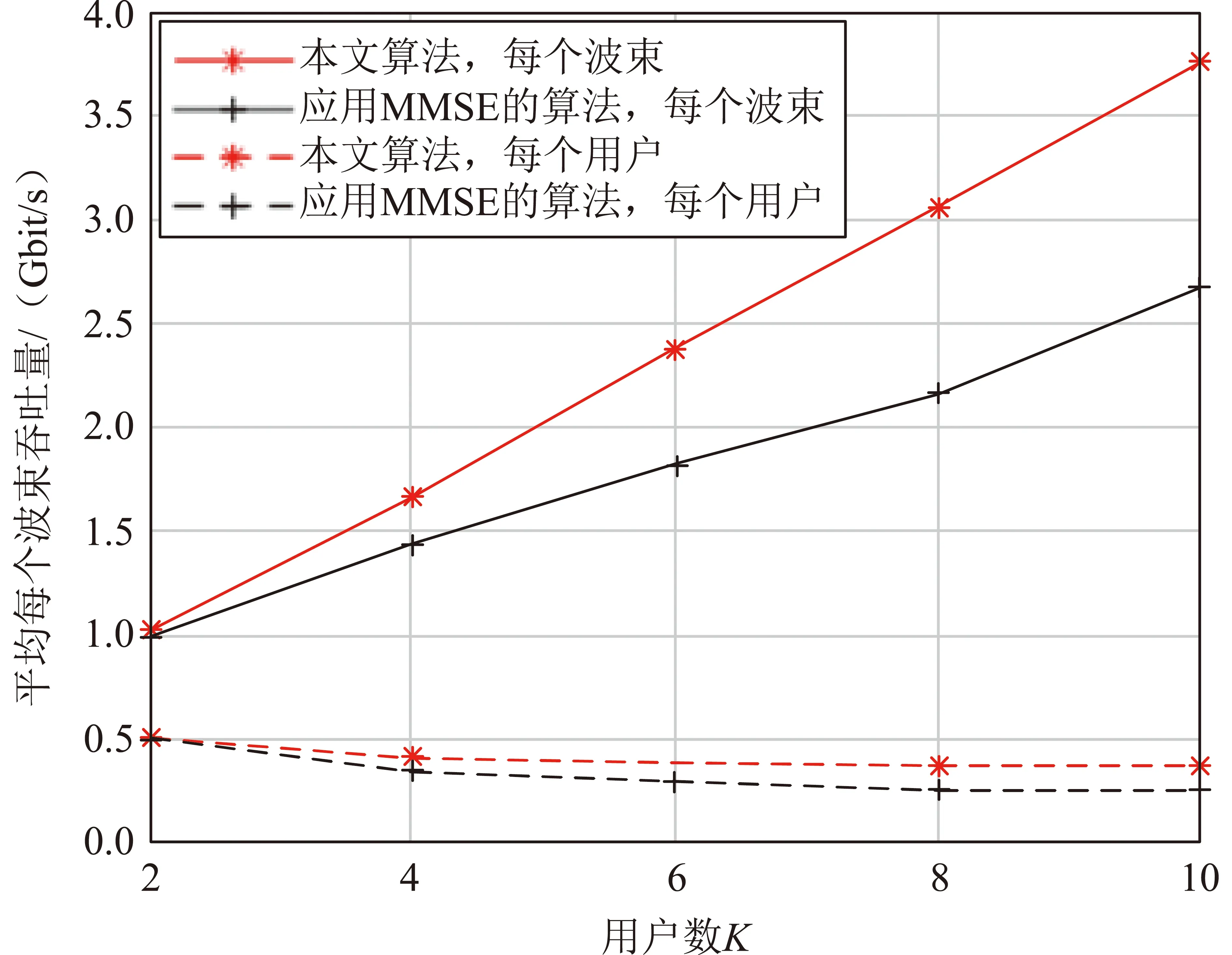
图4 平均每个波束的吞吐量Fig.4 Average throughput of each beam

由图3可知:当K为6时,本文算法的平均每个波束吞吐量为2.1485Gbit/s,而应用MMSE的算法的平均每个波束吞吐量为1.4717Gbit/s,前者比后者提升了46.0%,表明本文算法明显优于应用MMSE的算法,优势更突出。

图4表示每个波束调度的用户数对系统性能的影响,其中,实线表示用户数K取不同值时平均每个波束的吞吐量,虚线表示平均到每个用户的吞吐量。可以看出:随着调度的用户数K的增加,2个算法的每个波束吞吐量都在随之提升,但是平均每个用户的吞吐量随着调度的用户数的增加而降低。这是因为:随着调度的用户数增加,用户信道的差异性逐渐增大,针对最差用户信道进行的线性预编码设计会导致其他用户的性能损失越来越大,使得平均每个用户的吞吐量下降,但波束内调度的用户数还在增加,波束内总的吞吐量也在提升。

从图4中还可以看出:相比于应用MMSE的算法,本文算法在波束吞吐量上有明显的提升,通过迭代MMSE接收机、加权值及最小化加权MSE的方式优化线性预编码。其中:加权值为上一次迭代得到的MSE的倒数,这使得经过优化预编码后波束间吞吐量差异较小,系统整体的吞吐量提升。当用户数较少时,极端情况为单播场景,本文算法退化为加权MSE最小化算法,波束间的加权值较小,使得波束间功率平均分配,系统性能较差;随着用户数的增加,系统权重值依据多个用户的MSE来选择,迭代后不同波束之间的权重值有一定的差异,使得本文算法的平均每个波束吞吐量优于应用MMSE的算法。

图5为每帧内调度用户数K为6时,本文算法与应用MMSE的算法的平均每个波束吞吐量与星上总功率的关系曲线。可以看出:随着功率的增加,平均每个波束吞吐量近似与功率呈对数关系。在考虑的功率范围内,本文算法相比于应用MMSE的算法始终有25%以上的频谱效率提升。在较低功率范围内,本文算法的性能增益更显著,因此可以适应不同的功率条件,在考虑的功率范围内都能表现出更优的性能,且在功率较低时对频谱效率的提升作用更为明显。

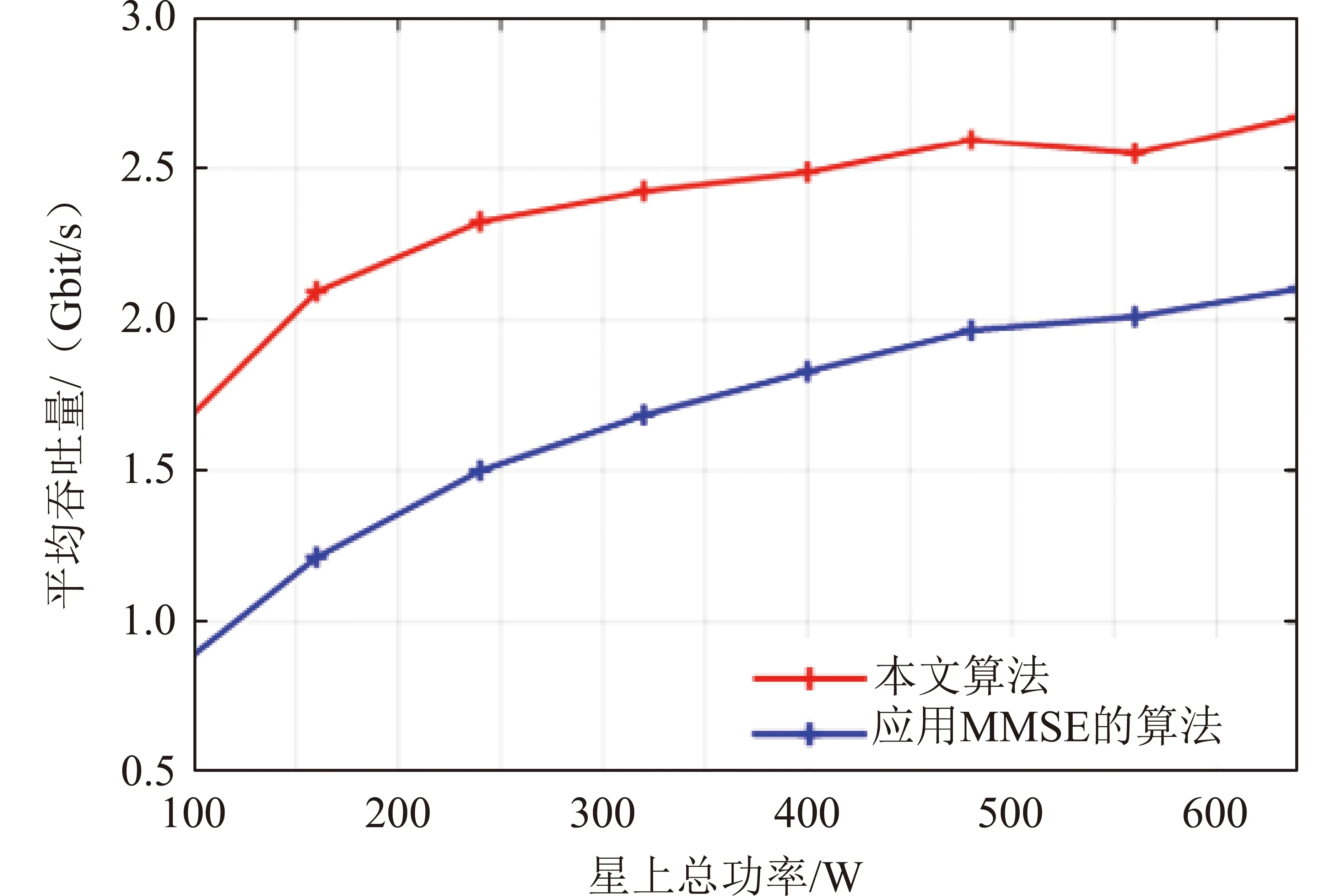
图5 平均每个波束吞吐量随星上总功率的变化Fig.5 Average throughput of each beam with different sum power

4 结束语

本文设计了VHTS通信系统多播场景下的线性预编码算法。考虑星上天线的功率约束,以最大化系统总吞吐量为目标,将最大化和吞吐量问题转换成与接收机联合设计的加权和均方误差最小化问题求解,并采用ADMM将加权均方误差最小化问题分解为多个并行求解子问题,得到每个变量更新的闭式解。仿真结果表明:本文算法与应用MMSE的算法相比,在不同功率和不同每帧用户数条件下都能实现显著的频谱效率增益,同时计算复杂度较低,可应用于后续全频率复用VHTS通信系统。