确定任务视角下集装箱堆场箱位分配研究
郑云峰,刘瑞麟,饶本顺,周校彬,张国庆
(大连海事大学 航海学院,辽宁 大连 116026)
0 引 言
目前的国际贸易运输中,集装箱运输杂货已经变得越来越主流。码头是运输过程中集装箱交接的直接场所,其空间以及机械设备资源都非常有限,而集装箱的运量却有增无减。因此,高效分配码头资源,提高码头前方堆场资源利用效率显得尤为重要,也引起了业界的重视。已有关于集装箱码头资源调度的研究,主要有堆场空间的分配和设备的调度2个方向,其中箱位分配和场桥调度是近年来学术界关注的热点。基于此,笔者从堆场空间和设备调度2个角度出发,研究箱位分配的问题。
关于集装箱码头堆场箱位分配问题的研究,可以根据是否考虑堆场不确定因素分为2类。一些学者假设存取箱任务已知,将不确定问题确定化,对问题进行简化,比如:R.DEKKER等[1]对不同箱位堆存策略分别进行了仿真试验分析,结果表明分类堆存方法明显要优于随机堆存方法;范厚明等[2]采取分区域堆存原则,考虑多场桥之间相互影响及所需的安全距离,建立了整数规划数学模型,得出给定批量任务的贝位方案;范厚明等[3]考虑多场桥作业的安全距离以及任务量均衡,构建数学模型,求解贝位分配问题;倪敏敏等[4]提出一种动态的多场桥分区域堆存方案,弥补了上述文献中为确保各场桥间的安全距离而带来的不足和缺陷;张灿荣等[5]提出累加重量的思想,将一个堆垛的总重量描述为所有集装箱重量的累加和,以最小翻箱量为目标,研究集装箱的贝内排箱问题;张煜等[6]在堆场堆存方案已知的基础上,研究船上箱位分配问题,分析不同派送方案对配载结果造成的影响。
一些学者考虑了堆场的不确定因素,采用滚动周期的方法把不确定问题转化一段时间内的确定问题进行建模求解,比如:K.H.KIM等[7]考虑集装箱在场时间,采取滚动策略构建混合整数规划(MIP)模型,利用启发式算法优化求解模型;周鹏飞等[8]考虑离港箱交箱时间的随机性,提出两级调度策略,建立数学模型求解;周鹏飞等[9]针对集装箱进出港时刻不确定,构建离港箱位随机双层规划模型,优化码头翻箱量以及场桥移动的行车成本;邵乾虔等[10]运用马尔科夫链预测处理随机的交箱序列,解决交箱时间不确定问题,并在实际进场顺序和预测顺序出现偏差时,对预测交箱顺序进行修正;刘婵娟等[11]考虑出口箱进场时间的不确定,将堆场的箱位分配问题分为两阶段,以集卡运输距离最小和贝内翻箱量最少为目标,构建多目标规划数学模型,使用Yalmip软件求解;郝振勇等[12]基于集装箱的重量等级建立数学模型,将随机到达堆场的出口箱按重量等级在贝位内分配具体箱位;武慧荣等[13]均衡码头各区域任务量,以滚动计划为基础构建混合堆场箱区分配数学模型,提出一种模拟退火算法对问题进行优化求解。
总的来说,国内外学者对箱位分配问题从多方面进行研究,已经取得了诸多成果,但仍存在一些不足。大多数学者将进场箱的贝位选择和贝内排箱看作2个问题,只解决其中一个问题,而不考虑另一个;或者使用二阶段求解的方法,依次解决2个问题,并未考虑2个环节之间的关系和影响。一旦确定贝位,箱位的位置就只能固定在很小的范围内,导致结果容易过早收敛并陷入局部最优。然而,箱位分配是一个连续的过程,各环节是互相耦合的。因此,笔者将考虑这个连续的过程,将2个阶段看作一个整体。
又因为不确定问题更加复杂,要考虑的因素更多,而笔者的研究侧重于一种解决箱位分配问题的方法,是否考虑不确定性对结果影响不大。因此笔者假设存取箱任务已知,简化求解模型。在此基础上,采取分区域平衡策划,考虑场桥移动成本和翻箱成本,构建以场桥移动和翻箱总成本最小化为目标的多目标混合规划数学模型,提出一种在整个区域内搜索排箱位置的遗传算法对模型进行求解。最后通过仿真实验,并与Yalmip求解工具箱进行对比,验证算法的可行性和优势。
在理论上,提出了一种新的箱位分配思路,丰富了集装箱堆场箱位分配的研究内容,使研究成果更符合实际情况,具备实用性;实践上,为码头实际工作提供一种可行参考对策。
1 问题描述
集装箱堆场箱区的箱位一般用贝(bay)、列(row/slot)、层(tier)表示,进场的每一个集装箱都对应唯一的位置表示,记作P(i,j,k)。每个集装箱目的港、离港时间、重量等都不相同,按照这些属性将集装箱分组。笔者采用分区域堆放的方法,将堆场箱区划分为不同区域,不同组的集装箱储存在相应的区域内。每个集装箱进场时,根据箱子的信息,将箱子分配在合适的位置。这样做使得搜索贝的范围扩大了,不同于以往一旦确定了贝位,箱位分配只能在单个贝位中选择,选择范围小,解的搜索限制在小范围内容易局部收敛,造成集装箱堆积。分区域策划下,箱位选择的求解过程可以有更大的搜索范围,更有利解的多样性和接近最优解。
堆场在完成堆存作业时,每个集装箱所分配的箱位不同,如果相邻的2个集装箱在不同贝内,场桥就必须要移动贝位才能完成装卸工作;如果某个集装箱上已经堆存了其他箱子,要先将其上面的箱子转移到别的位置,再开始进行作业,这就出现了翻箱。所以如果集装箱在堆存前没有合理规划,分配合适位置,就会导致很多不必要的场桥移动和翻箱,进而影响码头的工作效率。而场桥移动和翻箱都有一定的成本,所以箱位分配问题就可以转化为求解最小场桥移动和翻箱量总成本问题。
同时为简化数学模型,笔者作出以下假设:
1)进场集装箱规格一致,且采取先到先服务原则。
2)集装箱按照目的港、离港时间、重量等属性分组,同种集装箱在同一区域。
3)集装箱预约进出场的时间、重量、目的港,堆场的剩余容量等信息已知。
4)按同尺寸、同目的港的出口箱堆存,贝内不同重量级按重压轻堆存。
2 模型建立
2.1 符号说明
I为堆场的贝数;J为堆场的列数;K为堆场的层数;N为进场箱的总数;M为一个充分大的正数。
Cn为第n个进场箱的属性值,其值越大的集装箱,越早离开码头、重量越大。Cn可根据目的港编号,交箱时间,重量计算得到,计算公式为:
Cn=k1×p+k2×t+k3×w+k4×n
(1)
式中:p为目的港编号。为便于装船,同目的港的集装箱需集中堆存,将作业区域按贝位划分为不同子区域存放不同目的港的集装箱。目的港编号越大,说明对应子区域的集装箱越早装船。t为离港时间等级。将离港时间划分为不同时段,每个时段对应不同的时间等级。时间等级越大说明离港时间越早。w为集装箱重量等级。将重量划分为不同重量段,每个重量段对应不同重量等级。重量等级越大说明集装箱的重量越大。n为集装箱进场序列。k1,k2,k3,k4分别为根据堆场规模和实际需要确定的系数,分别决定不同因素对属性值的影响。
Ti为第i贝的初始箱量;Pnijk为箱位(i,j,k)是否堆存出口箱n,分别用0或1表示,即:
(2)
式中:i=1,2,…,I;j=1,2,…,J;k=1,2,…,K。
Rnijk为出口箱n堆存在箱位(i,j,k),对下方箱位(i,j,k-z)的出口箱m是否存在翻箱,分别用0或1表示,即:
(3)
式中:i=1,2,…,I;j=1,2,…,J;k=1,2,…,K;z=1,2,…,K-1。
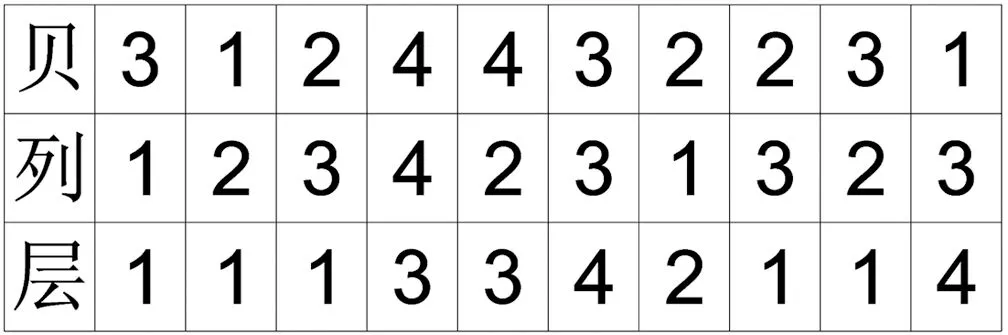
图1为一个贝内的翻箱现象,方框内的数字表示该位置所放置集装箱的属性值Cn,空值表示该位置空箱。按照堆存规则,属性值越大越早离开码头,位置越靠上。若某箱下面存在属性值更大的集装箱,即Cn 图1 翻箱现象 Fig. 1 Container turning phenomenon 箱位分配的目标有2个,分别是场桥移动的行车成本最小和作业的翻箱成本最小。其中场桥贝内移动距离最短的目标函数为: (4) 翻箱量最小的目标函数为: (5) 综合以上2个目标函数,构建总成本目标函数: Z=min(α×Z1+β×Z2) (6) 式中:α为场桥跨越一个贝位的行车成本;β为一次翻箱的成本。 约束条件为: (7) (8) (9) (10) (11) (12) (13) (14) 模型中式(7)为一个集装箱只能存放在一个箱位内;式(8)为一个箱位最多只能堆存一个集装箱;式(9)为场桥的初始位置在贝位1;式(10)为分配在贝位i的集装箱数量要小于堆场容量;式(11)为不能出现悬空堆放的情况;式(12)为上层晚于下层放箱, 其中M是一个足够大的正数。 当(i,j,k)存在集装箱时: (15) 此时上层箱进场序列n,大于下层箱进场序列n。即上层晚于下层放箱。 当(i,j,k)没有集装箱时: (16) 此时式(12)仍然成立,并符合实际情况。 式(13)表示(i,j,k)的集装箱晚于(i,j,k-z)离港时,记一次翻箱, 其中M是一个足够大的正数。 当(i,j,k)存在集装箱时: (17) 此时,若上层箱属性值小于下层箱属性值,为使公式成立,必须使Rnijk=1,即发生翻箱;若上层箱属性值大于下层箱属性值,Rnijk=0也可使公式成立,即不翻箱。 当(i,j,k)没有集装箱时: (18) 此时式(13)仍然成立,并符合实际情况。 式(14)表示进场箱需要堆存在所分配的箱区,其中min和max分别为该箱区所容纳集装箱属性的最小和最大值。 在分区域平衡策划下,根据已知的集装箱到港信息表和堆场剩余容量信息,将不同属性的集装箱分配在堆场的不同区域,确定箱位分配方案。笔者设计一种遗传算法优化求解数学模型。 笔者选用实数编码,每条染色体为3行n列的矩阵,每行分别表示集装箱分配的贝、列、层。染色体长度对应进场箱的数量,每一列的3个数即表示一个集装箱在堆场中的坐标。不同染色体对应不同的堆存方案,如图2。图2中:10个集装箱分配在4个贝位的箱区内,第1列表示第1个集装箱分配的位置为(3,1,1)。 图2 染色体示意Fig. 2 Chromosome diagram 在约束条件下,根据已知的集装箱和堆场信息,得到每个集装箱的属性值,以及堆场的堆存情况,确定集装箱的堆存区域,随机生成初始种群。检查生成的种群,对不满足约束的染色体进行修正,使其满足约束。 计算种群中每条染色体所对应的适应度函数,得到相应的目标函数值。采用轮盘赌的选择方法,由于目标函数要求最小值,将目标函数取倒数,使种群中函数值较小的基因更具优势,更容易遗传到下一代,从而实现种群的优化。 交叉采取两点交叉的方法。如图3,首先在2个父代个体确定交叉位置,之后将2个父代的前半段和后半段进行交叉遗传给2个子代,得到新的子代个体。最后检查子代个体的染色体,修正不满足约束的子代染色体。 图3 交叉操作Fig. 3 Cross operation 变异操作采用单点变异的方式。如图4,首先在父代个体上确定变异点,根据约束条件以及该变异位置所在贝的堆存情况确定变异范围,进行基因变异,使得该位置的集装箱的坐标发生变化。最后检验子代个体的染色体,修正不满足约束的子代染色体,使染色体满足约束并遗传到下一代。 图4 变异操作Fig. 4 Mutation operation 当算法的遗传操作达到设定的最大迭代次数时,算法结束,此时得到的排箱方案即为最佳方案,对应的函数值即为最优值。算法流程如图5。 图5 算法流程Fig. 5 Algorithm flow 算法具体求解过程为:根据已有的集装箱进出场信息表和码头现有的堆存情况,确定染色体的编码长度以及数学模型各个约束的范围。设定所需的初始参数,如迭代次数,种群规模,交叉概率,变异概率等,随机生成满足约束的初始种群,开始算法的迭代,直到满足终止规则,算法结束。 仿真实验的堆场规模为20×4×4(贝×列×层),配备一台场桥;考虑到堆存作业时会出现翻箱,每贝位最多堆存12个出口箱,即预留4个翻箱位。某时刻共有30个装卸任务,该任务的集装箱的到港信息已知,如表1。其中交箱时间等级越大意味着越早交箱,重量等级越大意味着重量越大。各贝位的堆存情况和根据区域策略相对应的目的港已知,如表2。根据场桥的技术参数和港口规范,经计算得场桥移动一个贝位成本是0.56元,翻箱一次成本是4.47元。 表1 出口箱的目的港和重量级属性信息Table 1 Destination port and weight attribute information of export box 表2 各贝位初始箱量和对应目的港Table 2 Initial container quantity of each bay and corresponding destination port 根据堆场规模,并结合实际情况,假设箱位分配优先考虑级分别是:目的港,离港时间,重量,进场序列。Cn的计算系数k1,k2,k3,k4分别取100 000,10 000,1 000,1。 为了验证笔者算法的性能,在软件MATLAB R2016b中完成代码的编写,设定迭代次数为400,种群规模为100,交叉概率为0.6,变异概率为0.001。对该算例求解可知,随着算法不断地迭代,各代种群的目标函数和相应翻箱量变化情况如图6。 图6 结果收敛Fig. 6 Result convergence 在图6中:算法迭代到140代,目标函数收敛于59.92。此时翻箱量为0,成本只有场桥移动的费用,即为59.92元,目标函数值最小,对应的排箱方案即为最优方案。 具体的集装箱堆存方案如表3,每一行分别表示一个集装箱被分配贝列层的位置坐标以及其所具有的属性值。 表3 分配实验结果Table 3 Results of distribution experimental 根据k1,k2,k3,k4的取值情况,属性值Cn第1位数字表示目的港,第2位数字表示离港时间等级,第3位数字表示重量等级,后3位数字表示进场序列。 从表3可以看出,目的港不同,即Cn第1位数字不同的集装箱,被分配在不同的子区域:目的港为1的集装箱{2,3,5,8,10,12,13,14,15,16,17,18,19,23,27,28,30}被分配在1~9贝;目的港为2的集装箱{1,4,6,11,20,24,25,26,29}被分配在10~15贝;目的港为3的集装箱{7,9,21,22}被分配在16~20贝。符合分区域平衡策划的堆存规则。 在同一堆栈,即贝列相同的集装箱:{(1,11),(2,8,10,13),(3,28),(5,17),(18,30),(19,23),(21,22),(25,29)},上层属性值大于下层属性值,满足先交箱压后交箱,重箱压轻箱策略堆存。 同时每个集装箱贝列层坐标均不同,不存在一个箱位存放多个箱子的情况;所有集装箱都在第一层,或者下层存在集装箱,没有悬空放箱的现象。满足约束条件。以上说明了笔者算法解决箱位分配问题的有效性,并且适应实际情况。 笔者针对不同规模的算例进行仿真,将仿真优化的结果与Yalmip求解结果作对比,对比结果如表4。仿真实验使用的遗传算法属于启发式算法,所求解是一个近似值,因此实验结果使用5次实验的平均值。 表4 对比实验结果Table 4 Results of comparative experiment 从表4中可以看出,Yalmip软件求解小、中、大规模问题都可获得最优解,但大规模的场景案例求解时间较长,且无法求解超大规模算例。笔者设计的算法在小规模场景得到的解和Yalmip软件的结果一致;中规模场景得到的解逼近Yalmip所求解,开始出现小的求解误差,并且实验规模越大求解误差越大;对于大规模场景求解的时间远小于Yalmip,所得解产生的误差依然在可接受范围内;甚至可以解决Yalmip不能解决的超大规模问题。这是因为随着实验规模的扩大,所需的求解时间在所难免会变长。笔者提出的算法在整个群体中搜索可行解,可以同时比较多个个体的性能,有很好的并行性,减少了不必要的计算,节约了迭代时间。在任何规模的场景下,能够在可接受时间内求得最优解或者近优解,说明笔者算法在求解箱位分配问题具有优越和显著的性能。 针对确定任务视角下的单场桥堆场的箱位分配问题,使用分区域堆存的策略,综合考虑场桥行车成本和翻箱成本,构建针对此问题的整数规划数学模型,提出一种区别于二阶段法的遗传算法,不必先确定贝位,再贝内排箱,与堆场的实际作业的情况更相符。仿真实验结果表明:使用的分区域堆存策略能够有效地解决箱位分配问题;提出的算法可以有效减少场桥在作业过程中的移动距离和翻箱量,减少不必要的装卸成本,从而提升码头堆场的工作效率;由于数学规划的求解效率会随着规模增大而快速衰减,对不同规模案例,将文中算法与传统求解软件Yalmip的求解结果相比较,可知笔者提出的算法对大、中规模模型的求解效率更具有优势。算法具备一定的理论意义,可以应用于堆场作业时的箱位堆存问题,对实际操作具备一定的借鉴意义。 因为笔者只是考虑任务量已知的情况下的单场桥调度,实际到港信息会出现偏差,也可能是多场桥共同作业。未来可以考虑不确定问题下的排箱问题,以及考虑多场桥之前的互相影响。
2.2 堆场箱位分配模型
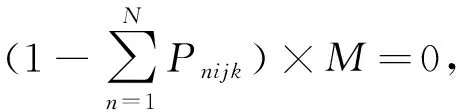

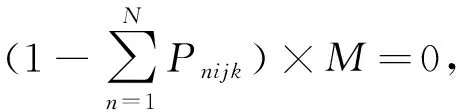
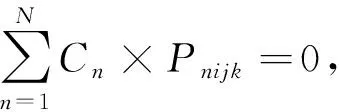
3 求解算法
3.1 染色体编码方式
3.2 种群初始化
3.3 适应度函数与选择操作
3.4 交叉操作
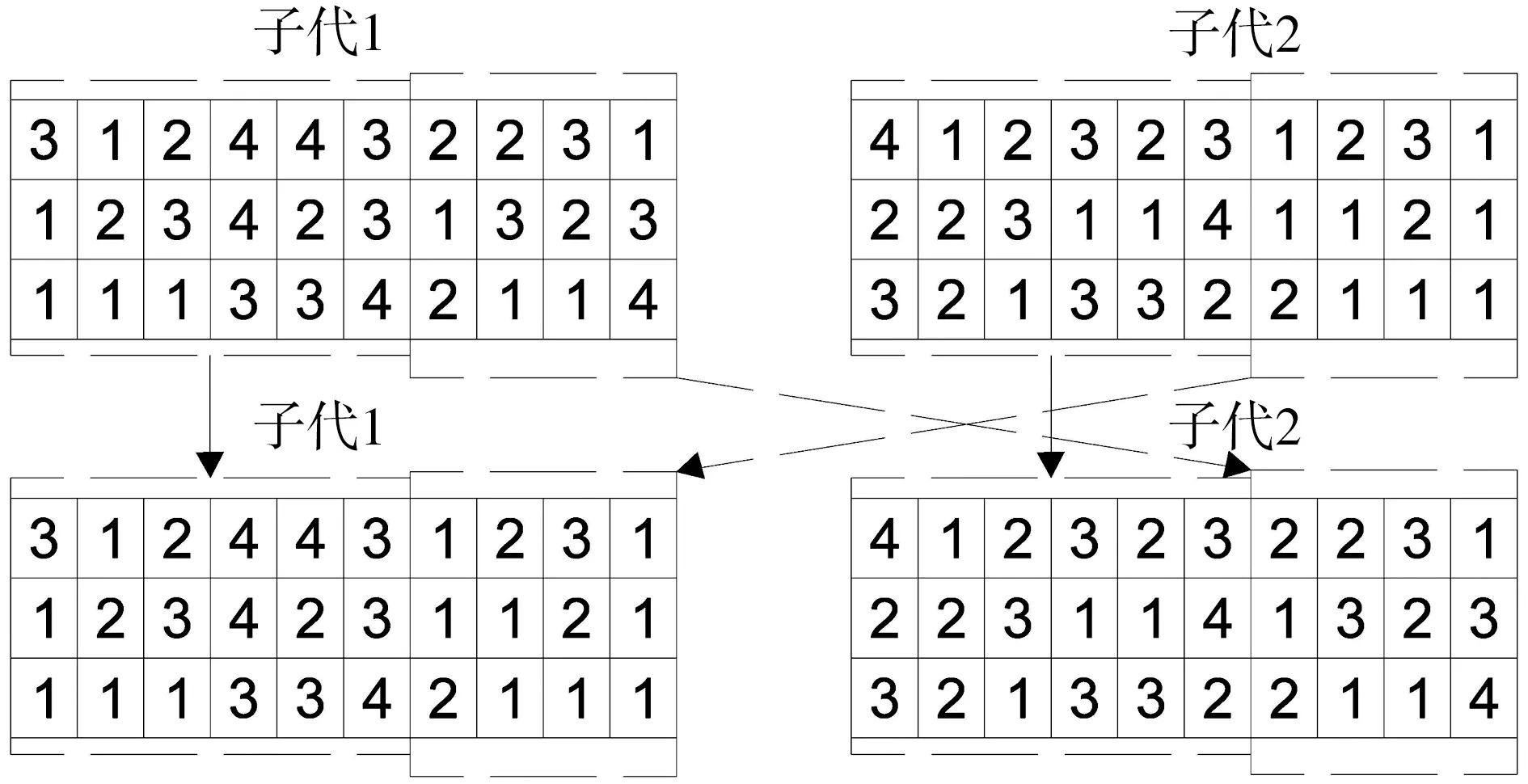
3.5 变异操作

3.6 终止规则

4 仿真实验
4.1 算例描述


4.2 结果分析与比较



5 结 语

