锅炉热效率加权平均及其不确定度评定的方法

齐国利 张松松 笪耀东

（1.国家市场监管重点实验室（特种设备安全与节能)，中国特种设备检测研究院 北京 100029）

（2.中特检验集团有限公司 北京 100029）

对于锅炉热效率的测量，实际上需要测量温度、压力、质量和质量流率等参数，按照能量平衡原理（锅炉热工性能试验，也称作热平衡原理），实际上就是把整个热力系统作为一个平衡系统，不用考虑进出口阻力损失等，只考虑热量平衡[1]。锅炉产品验收或鉴定试验时，热效率测试可以进行2 个或多个工况，在用定期能效测试时一般可以是1 个工况，无论是1 个或多个工况的试验，热效率计算所用的温度、压力、流量等参数都要进行若干次的测量，以减少测量不确定的影响[2-3]。对于锅炉产品能效测试，其热效率应进行2 个工况（或2 组）的测试，锅炉热效率取2 个工况热效率的算数平均值[4]。ASME PTC 4：2013《锅炉性能试验规程》规定，为了减少试验不确定度，可进行多组试验，满足重复性标准的多组试验结果取平均值得到平均试验结果，没有给出平均试验结果的不确定度计算方法。EN 12952-15：2003《水管锅炉和辅助设备 第15 部分：性能验收》规定，热效率试验结果乘以热效率的相对不确定度获得热效率的绝对不确定度，测量效率加上热效率的绝对不确定度应当大于保证或者设计效率[5-6]。但遗憾的是，ASME PTC 4：2013和EN 12952-15：2003 都没有能够给出热效率平均值的计算方法及其热效率平均值的不确定度。

如果锅炉热效率测试结果进行了不确定度的评定，则不能使用算数平均值作为热效率测试结果，因为2个工况的热效率测试不确定度不同[7]，因此需要用更为科学的不确定度评定方法对热效率平均值进行不确定度的评定。

锅炉热效率测试中温度、压力、热值、质量和质量流率等参数的测量[8-9]，都是基于高斯（正态）分布，比如给水质量流量通过大量测量，给水质量流量分布应符合高斯分布，但由于时间等成本问题，质量流量测量不可能是无限次的测量，一定是有限次的测量，各类测量标准一般都给出最小的测量次数，可以通过平均值的标准偏差判断测量结果的质量[10]。

本文基于试验结果应符合高斯分布的基本原理，推导了锅炉热效率及其不确定度加权公式，获得了锅炉性能试验结果及其不确定度的表征方法。

1 热效率的加权平均值

如果2 组热效率测试结果都服从高斯分布[11]，第1 组热效率试验得到的热效率值ηA的概率见式（1）。

式中：

Pη（ηA)——第1 组试验获得的热效率值ηA的概率；

η——热效率的未知真值；

σA——第1 组试验获得的热效率标准差。

第2 组热效率试验得到的热效率值ηB的概率见式（2）。

假设同样条件下，进行一次完整的试验，包括第1 组热效率试验获得ηA的概率与第2 组试验获得ηB的概率，2 次概率相乘，可以写成式（3）。

式中：

从最大似然原理可以看出，对未知真值η的最佳估计是实际测量热效率ηA和ηB的最可能的值。即η的最佳估计值是使式（3）的概率取得最大的那个值[12-13]。利用最小二乘法原理，把式（4）对η求导，导数等于0，见式（5）。

用第1 组和第2 组试验的热效率标准不确定度进行表示，见式（6）。

式中：

uA——第1 组试验获得的热效率标准不确定度；

uB——第2 组试验获得的热效率标准不确定度；

N——试验次数。

式（6）进一步整理得式（7）。

式（7）进一步整理得式（8）。

定义权见式（9）。

式（8）可以进一步写为式（10）。

如果2 组试验的热效率不确定度相等，那么热效率最佳估计值就是算术平均值，若2 组试验的热效率不确定度不一致，则不能使用算数平均值进行平均。从式（9）和式（10）可知，标准不确定度越小，权值越大，热效率测试结果越接近热效率的最佳估计值。

当然，式（10）也可以推广到多组试验情况，见式（11）。

2 热效率平均值的不确定度

式（9）可以推广到多组试验的情况，见式（12）。

式（12）变形整理，见式（13）。

平均值的标准偏差见式（14）。

则热效率平均值的标准偏差见式（15）。

进一步整理得式（16）。

这是由于加权平均值ηwav是原测得值η1，η2，……，ηn的函数，因此ηwav的不确定度可以通过误差传播的方法计算出来[13]。

3 热效率不确定度的典型计算示例

以NB／T 47066—2018《冷凝锅炉热工性能试验方法》的附录中F.10 的冷凝锅炉反平衡热效率相关数据作为第1 组数据，假设该台锅炉的另一组数据进行计算和比较，具体见表1。

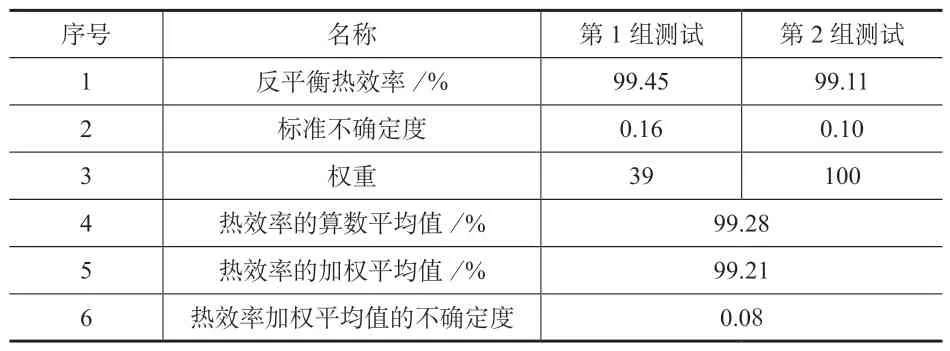
表1 锅炉热效率平均值的计算

从表1 可以看出，热效率的算数平均值为99.28%，热效率的加权平均值为99.21%，由于第2 组的权重更高，因此热效率的加权平均值更接近第2 组热效率。由于2 组热效率的权重差异不是特别大，因此热效率的加权平均值虽然更接近第2 组，但仍然有第1 组的影响存在。如果做另外一个假设，第1 组测试的标准不确定度是第2 组的4 倍，具体数值见表2。

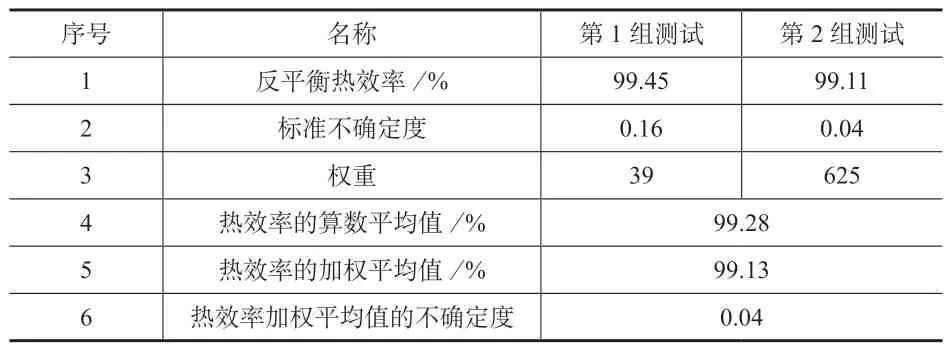
表2 锅炉热效率平均值的计算（假设）

从表2 可以看出，当第1 组测试的标准不确定度是第2 组的4 倍时，第2 组的权重几乎是第1 组权重的16 倍，即平方关系。2 组热效率的加权平均值为99.13%，与第2 组热效率基本一致，也就是说，当2组测试的标准不确定度相差3 倍以上时，可以不考虑不确定较大的测试组，热效率的加权平均值就是热效率测试不确定度权重较高的实测热效率。

较高的标准不确定度是较低的标准不确定度的倍数关系符合什么条件才可以考虑较高组的测量数值，或者忽略较高组的测量数值。把不同组的标准不确定度与热效率加权值的标准不确定度的关系作成图1。从图1中可以看出，当两者的倍数关系符合3倍以上时，可以考虑忽略较高组的数值影响。从2 组热效率测量质量方面考虑，2 组数据的标准不确定度越接近越好，当其相等时，2 组热效率可以取算数平均值，这是一种极端情况，GB／T 10180—2017《工业锅炉热工性能试验规程》的2 组热效率取算数平均值就是假设这种极端情况，显然，这是不合理的，因此在进行2 组热效率取平均值时，应采用加权平均值。

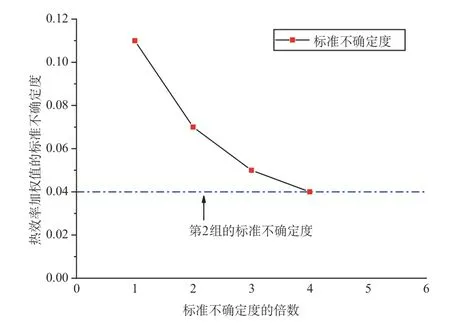
图1 标准不确定度的倍数与热效率加权值的不确定度的关系

4 结论

锅炉热效率测试是评价锅炉能效状况的主要手段，因此TSG 91—2021《锅炉节能环保技术规程》规定了锅炉热效率限定值的要求。从常用的测试标准可知，锅炉产品热效率测试数据取2 次热效率测试的算数平均值，如果从不确定度的角度分析这是不科学的。因此，本文从理论上分析了热效率测试结果应是2 组测量的加权平均的可行性，并提出了2 组测量加权平均的计算方法和加权平均值的不确定度计算方法。另外，通过示例分析了2 组测量标准不确定度差异对加权平均值不确定度的影响规律，提出一般2 组标准不确定度的倍数超过3 倍，则可以忽略较高不确定度的测量热效率，在测量中应尽量减少2 组测量标准不确定度的差值。