一种大状态轻量级密码S盒的设计与分析
樊 婷,冯 伟,韦永壮
(1.桂林电子科技大学 广西密码学与信息安全重点实验室,广西壮族自治区 桂林 541004;2.广西网信信息技术有限公司,广西壮族自治区 南宁 530000)
1 引 言
随着后量子密码、认证加密算法等研究的发展,为了提高密码算法的安全性以及适用于更广阔的物联网应用环境,需要对轻量级分组密码算法的分组长度和密钥长度提出新的安全需求。2018年,美国国家标准与技术研究院启动轻量级密码算法征集计划,接受软硬件性能突出且适用于资源受限环境中的轻量级认证加密方案和哈希算法,2021年宣布10个算法入围最终轮[1]。2018年8月,我国面向全国的密码研究团队,启动了分组密码算法设计竞赛[2]。2019年8月公布了进入第二轮的10个候选算法,10月进入最终评选,uBlock[3]和Ballet算法[4]获得了一等奖。在许多轻量级密码竞赛中,越来越多的方案采用大状态置换,规模为256 bit甚至512 bit的大状态分组密码或内部置换被提出,如KNOT[5]、Gimli[6]和SPARKLE[7]等。叶涛等[8]于2021年基于“标志位”技术,通过构建密码S盒的新可分性模型,搜索到KNOT-256密码算法的30轮零和区分器。2022年,谭豪等[9]首先根据“与操作”的差分传播规律,为Gimli置换设计了一个差分传播系统,找到了7轮不可能差分区分器。然后向前扩展4轮,实现了11轮Gimli认证加密方案的状态恢复攻击。SPARKLE作为入围NIST轻量级密码竞赛的10个最终候选算法之一,由于非线性部件采用64 bit S盒-Alzette[10],其安全性同样备受业界关注。
Alzette是由BEIERLE等[10]提出的一种新型大状态轻量级S盒,模加是唯一的非线性部件,循环移位量也经过了特殊选取,整个结构提供了强大的安全性来抵御许多经典攻击。Alzette作为S盒来构造密码算法,其安全性问题引起了众多密码学者的关注。2022年,许峥等[11]将 Lipmaa-Moriai限制条件与符号差分相结合,提出了一种基于可满足性问题来搜索Alzette不可能差分区分器的自动化分析工具。在旋转异或分析方面,HUANG等[12]扩展了模加运算中旋转异或密码分析的概率传播公式,给定任意旋转参数,能够实现Alzette的旋转异或差分概率的计算。LIU等[13]在2021年欧密会上发表的文章中将差分-线性密码分析中的差分部分替换为旋转异或差分,对4轮Alzette展开了分析。尽管如此,如何计算任意输出掩码的旋转差分-线性相关性仍然未知。2022年美密会,NIU等[14]针对此问题给出一种计算任意线性输出掩码的 (旋转) 差分-线性相关性的有效算法,并基于该算法推导出一种评估ARX密码(旋转)差分线性相关性的技术,得到了Alzette更精确的旋转差分-线性相关性的值。2023年,LIU等[15]推广了MORAWIECKI等[16]分析Keccak[17]的技术,找到了Alzette相关性为2-0.27的4轮差分-线性区分器和相关性为2-11.37的4轮旋转差分-线性区分器。很显然,对于Alzette安全性分析大多处于低轮次的研究。这是由于Alzette是一个大状态的S盒,通过直接计算差分分布表 (Difference Distribution Table,DDT) 和线性逼近表 (Linear Approximation Table,LAT) 来评估其抗差分类/线性类分析的能力是无法实现的,突出了Alzette安全高效的特点。然而迄今为止,基于ARX结构的64 bit轻量级S盒并不多,是否存在基于ARX结构的新型大状态轻量级S盒,如何设计出性能与安全都达到最优的大状态轻量级S盒,也是研究的热点。
鉴于上述存在的问题,笔者提出了一种“层次筛选法”。通过提前设置最优差分特征/线性逼近的概率值,结合混合整数线性规划 (Mixed Integer Linear Programming,MILP) 技术构建了差分/线性密码分析的自动化分析模型,确定了最佳循环移位参数,设计了一种基于ARX结构的64 bit轻量级密码S盒。结果表明:当迭代轮数R=5时,新密码S盒的最优差分特征 (线性逼近) 的概率为2-17(2-8),而此时Alzette最优差分特征 (线性逼近) 概率为2-10> 2-17(2-5> 2-8),表明了新密码S盒抵抗差分和线性密码分析的能力都达到了最佳。迭代6轮,新密码S盒的最优差分特征概率为2-17;迭代 7轮,新密码S盒的最优线性逼近概率为2-17,在抗差分/线性密码分析方面表现出更卓越的性能。
2 基本知识介绍
2.1 符号说明
文章使用的符号如下所示:
2.2 Alzette简介
BEIERLE等提出的Alzette对64 bitX=(X1‖X0)输入状态进行置换,其中,X1=(x63,…,x32),X0=(x31,…,x0),如图1所示,分为左右2部分进行操作,每部分长度为32 bit。Alzette包括模加、异或和循环移位3种运算,c是轮常数。Alzette实例运算如算法1所示。图1为Alzette实例结构图示。
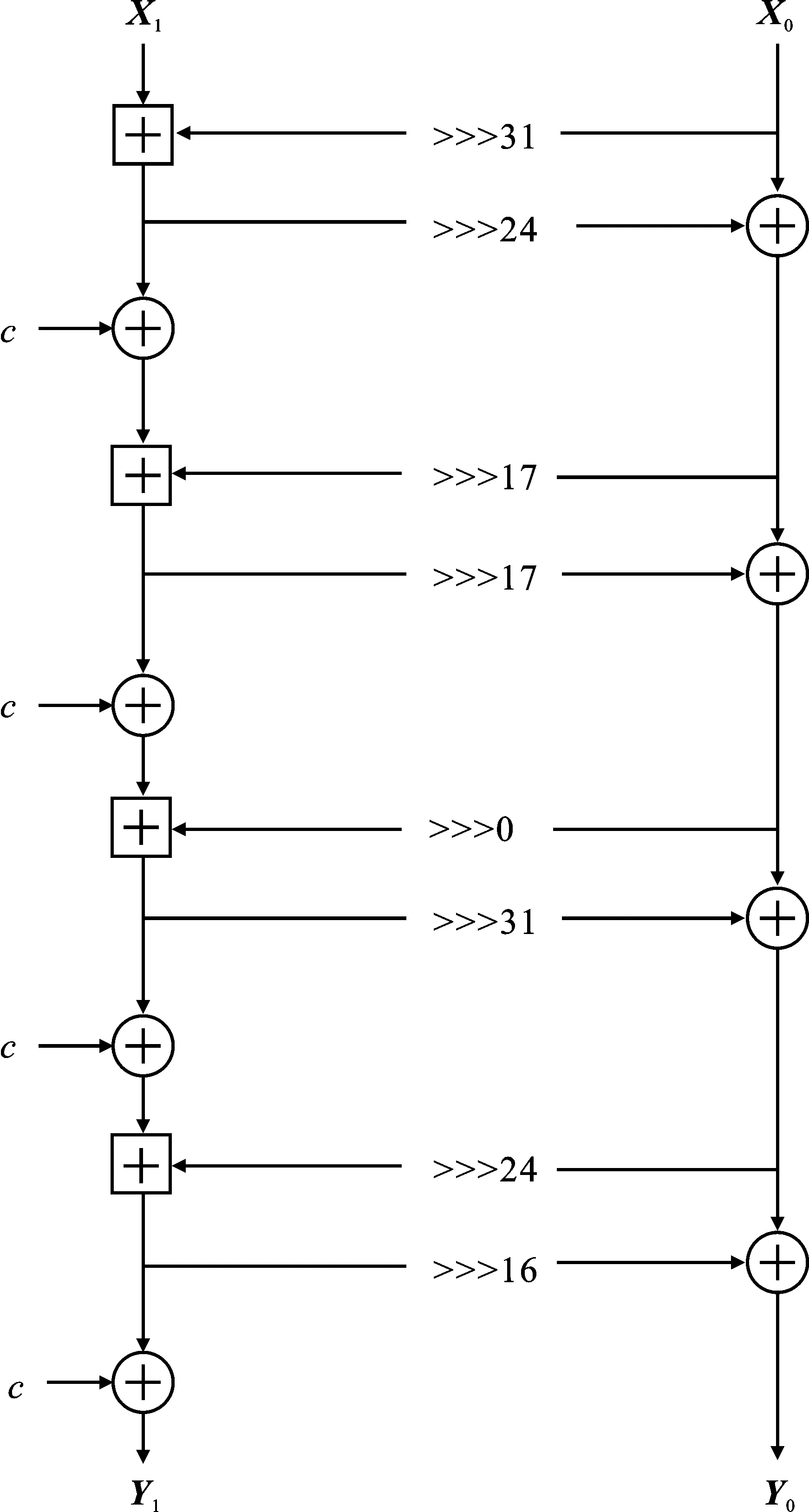
图1 Alzette实例
算法1Alzette实例。
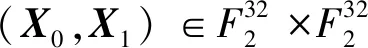
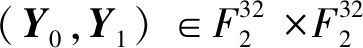
①X0←X0(X131)

③X0←X0⊕c
④X0←X0(X117)

⑥X0←X0⊕c
⑦X0←X0(X10)

⑨X0←X0⊕c
⑩X0←X0(X124)
2.3 预备知识
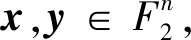
xy=x⊕y⊕carry(x,y) ,
(1)
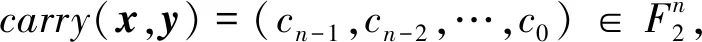
(2)


(3)


(4)
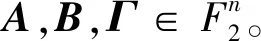
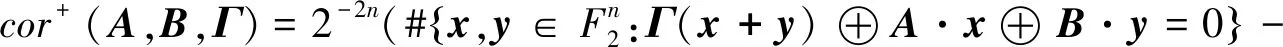
(5)
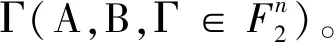
cor+(Γi,Ai,Bi)=LMkn-1Mkn-2…Mk1Mk0C,
(6)
其中,Mr(0≤r≤7)表示2×2的矩阵,且
L=(1,0)是行向量,C=(1,1)T是列向量。
(7)
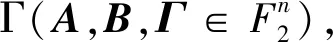
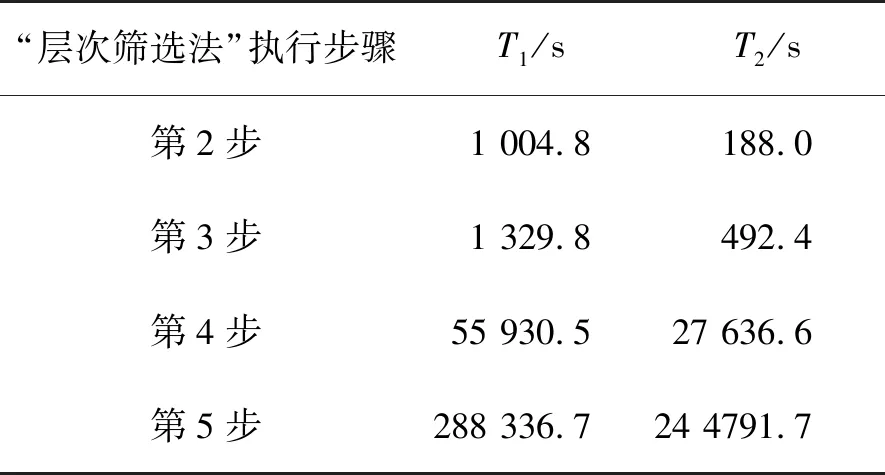
|cor+(Γi,Ai,Bi)=2-#{0 (8) 混合整数线性规划问题是运筹学中的一类优化问题。目前,解决该优化问题最常见的求解器是Gurobi[22]软件。在密码分析领域,往往使用不等式来刻画密码算法的各个操作,目的是先将密码分析问题转化为运筹学中的MILP问题,然后进行求解,代替传统的手工推导。为了抵抗差分/线性密码分析,通常要求最优差分/线性特征概率要远远大于随机置换概率。Alzette算法不包含S盒操作,唯一的非线性操作是模加。因此,只需要对Alzette的线性操作和模加操作构建模型,即可实现对Alzette算法抵抗差分/线性能力的评估。本节中,分别阐述最优差分特征和线性逼近自动化搜索模型的构建过程。 (1) XOR操作:对于a⊕b=c(a、b、c都表示单比特),用以下约束条件表示: (9) (10) (3) 分支操作:对于三分支操作,假设输入输出差分分别为a、b、c,则约束条件为a=b=c。 (4) 模加操作:使用文献[21]提出的针对ARX算法异或差分特征的MILP模型。主要思想是将定理1和定理2进行刻画,转化为不等式约束条件。用(αi,βi,γi,αi+1,βi+1,γi+1,eq(αi,βii,γi))刻画第i与第i+1比特差分值之间的关系,其中eq(αi,βi,γi)用来计算差分概率。令eq(αi,βi,γi)=pi,用以下13个线性不等式即可表示出所有可能的56种差分模式。 (11) (5) 额外条件:限制输入差分只有1bit活跃,保证输入差分非零,即(x0,x1,...,xn-1)≠0。其中,n为分组长度。 (12) 与差分特征模型构建过程类似,假设模加操作的两个输入与连续的两轮之间都是独立的。 (1) 分支操作:对于三分支操作,假设输入掩码和输出掩码分别为a和b,c,用以下约束条件表示: (13) (2) XOR操作:对于a⊕b=c(a,b,c都表示单比特),则约束条件为a=b=c。 (3) 循环移位:与差分特征的自动化搜索模型中的循环移位操作约束条件相同。 (4) 模加操作:使用文献[21]提出的针对ARX算法线性逼近的自动化搜索技术。主要思想是将定理3和定理4进行刻画,转化为不等式约束。用(si+1,Γi,Ai,Bi,si)表示状态εi+1跳转到εi过程,如果εi=e0,si=0;εi=e1,si=1,其中si用来计算相关系数的绝对值。用以下8个线性不等式可表示出13种所有可能的模式: (14) (5) 额外条件:需要添加2个额外约束条件,首先限制输入掩码只有1 bit活跃,保证输入掩码非零,即(x0,x1,…,xn-1)≠0。其中,n为分组长度。其次,设置sn=0,保证初始状态εn=e0。 (15) 密码算法设计与评估相互促进,不可分割。在分组密码算法的设计过程中,首先要选择算法结构,然后再选择各个部件的参数,比如S盒规模、循环移位量和轮常数等。当结构和筛选的参数进行优化组合后,最终需要对设计的算法进行最后的软硬件性能评估和安全性评估。软硬件性能指标评估一般包括吞吐量、时延和硬件面积等,而安全性评估中最经典的是差分密码分析和线性密码分析。总之,设计算法的最终目标是选择一组最优的参数,能同时保证算法的安全性和软硬件实现效率。 4.1.1 结构设计 Alzette是以ARX结构为基础构造的S盒,可以用较低的硬件代价实现,对于一些资源受限的应用,此种低实现成本的S盒更容易构造满足物存联网终端设备需求的轻量级分组密码算法。在安全性方面,S盒的规模越大,随机产生的密码S盒的密码性能就越好,即具有高非线性度和低差分均匀性。为抵御差分密码分析和线性密码分析,同时也考虑到上述硬件实现成本,新密码S盒仍然基于ARX结构。新密码S盒结构如图2所示,图中给出的是4轮结构,每4轮称为一个“step”,每个step中包括4个模加操作、8个循环移位、4个异或、8个分支和4个轮常数加操作。由图可知,新密码S盒中每个step的硬件实现成本与Alzette是保持一致的。 图2 新密码S盒结构图 4.1.2 循环移位量 循环移位相当于扩散层,它的作用是将输出打乱、混合。循环移位量的选取不仅会影响软件实现成本,而且直接影响新密码S盒抵抗差分/线性密码分析的能力;如果扩散足够好,则抵抗差分/线性密码分析的能力则越强。这里,循环移位量的选取准则是以最小化软件实现成本、最大化安全界为目标。出于效率的考虑,引用文献[10]中测试Alzette实例的每个循环移位量所需要的软件实现成本,旨在当软件实现成本与Alzette相同时,寻找能够更好抵抗差分/线性密码分析的ARX盒。 表1 循环移位量的软件实现成本 为了减少搜索空间,首先要根据软件实现成本,计算循环移位量的可行方案。对比文献[10]中的软件实现成本表,当软件实现成本14≤cost≤15,且8个循环移位量对应的软件实现成本为(2.66,2.66,2,2.66,2.66,0,2,0)时,软件实现成本与Alzette相同,相应的循环移位量的取值如表1所示。将所有的情况进行排列组合,循环移位量的选取共有4 096种可行方案。然后将可行方案划分为两类:参数重复选取和非重复选取。例如,(t0,t1,t2,t3,t4,t5,t6,t7)=(1,1,15,17,31,24,0,16)为参数重复选取,因为该方案中t0,t1都为1;而(t0,t1,t2,t3,t4,t5,t6,t7)=(1,8,15,31,16,24,17,0),由于每个参数的取值都不同,属于参数非重复选取。经过计算,参数非重复选取的方案共有96种,如表2所示。然后,需要对96种方案进行安全性测试,节4.2给出了具体过程。 表2 96组参数 4.1.3 轮常数 添加轮常数目的是消除算法结构的对称性,保证轮与轮之间具有一定的独立性。文中构建的差分/线性分析的自动化搜索模型,不涉及异或轮常数的操作。因此,添加轮常数对实验结果无影响。图2中,c(rmod 8)表示新密码S盒的轮常数,其中r表示轮数,c0~c7取值为c0=b7e15162,c1=bf715880,c2=38b4da56,c3=324e7738,c4=bb1185eb,c5=4f7c7b57,c6=cfbfa1c8,c7=c2b3293d. 新密码S盒包含4种操作:模加、循环移位、异或和分支。在差分密码分析中,分支操作对差分状态无影响,因此只需要对模加、循环移位和异或操作进行建模。在线性密码分析中,异或操作对线性掩码无影响,只需要对模加、循环移位和分支操作进行建模。利用前面提出的自动化搜索模型,对参数非重复选取的96种方案进行测试。由于搜索空间大、耗时较长,为了提高区分器搜索概率,使用“层次筛选法”,并调用“回调函数”,测试新密码S盒的每轮最优差分特征/线性逼近。 “层次筛选法”是指通过提前设置每轮的最优差分特征/线性逼近的上界,筛选满足当前安全界的新密码S盒方案。如表3所示,每轮设置的最优差分特征/线性逼近的上界称为阈值,每两轮的阈值是完全相同的。由于新密码S盒的模加操作被包含在奇数轮中,因此只测试奇数轮,可得到每一轮的最优差分特征/线性逼近。但是,为了加快搜索进程,快速搜索到可满足当前安全界的最优方案,采用图3中的步骤进行筛选。如果满足当前步骤设定的阈值,则保留该方案,继续进行下一步测试,否则就从整个搜索空间中删除该方案。其中,Q1~Q5代表执行每一步测试后剩余的候选方案集合。 表3 新密码S盒最优差分特征/线性逼近的阈值 图3 “层次筛选法”执行步骤 “回调函数”是Gurobi求解器中的一个函数,可以跟踪优化过程的进度,在求解模型时提供了高级控制功能。有时候在求解过程中需要获取一些信息、提前终止优化等,这些功能需要通过“回调函数”来实现。举个例子,在进行安全性测试时候,需要运行一个MILP模型,当MILP模型在优化过程中显示的当前最优值小于设定的阈值时,就可以调用“回调函数”来提前终止模型,启动下一个模型。具体代码如下所示。 算法2回调函数。 ① def mycallback(model,where): //定义回调函数mycallback,model表示模型名,where表示回调函数触发点 ② if where == GRB.Callback.MIP: //当回调函数触发点为当前MIP时 ③ objval=model.cbGet(GRB.Callback.MIP_OBJBST) //令objval等于当前目标最优值 ④ if objval <= threshold value://如果objval小于给定的阈值 threshold value ⑤ model.terminate() //终止模型 在自动化分析模型中,通过调用回调函数,可以提前终止不满足要求的方案,缩短总体测试时间。图4给出经过“层次筛选法”每个步骤后的剩余候选方案数量。由图可知,执行第2步操作后,此时能满足安全上界的方案较少,候选方案数量从96减少到16,筛除了80种不满足的方案,为加快后续步骤的执行奠定了基础。从第3步至第5步,候选方案数量继续下降,保持递减趋势,表明了该方法是可靠的、有效的。进一步,为了体现“回调函数”对测试速度的影响,对比了使用回调函数和不使用回调函数2种情况下的测试时间,实验平台为Inter(R)Xeon(R)Gold 6148 CPU @ 2.40 GHz(内存224 GB),测试结果如表4所示。其中,T1表示不使用回调函数时的测试时间,T2的表示使用回调函数的测试时间。由于第1步测试时间较短,在不使用“回调函数”的情况下仅用11秒就可以完成测试,因此这里给出第2步至第5步的对比结果。由表4可知,无论执行第几步,使用“回调函数”的情况下测试时间更短,尤其在执行第2步时,T2比T1提升了约5.4倍。 表4 测试时间对比 图4 “层次筛选法”过程中候选方案数量变化 经过测试,最终搜索到2种满足条件的方案,具体结果见表5。这2种方案的8个循环移位量分别为(t0,t1,t2,t3,t4,t5,t6,t7)=(1,17,8,15,31,16,24,0)和(1,17,24,15,31,16,8,0)。与文献[10]中Alzette的安全性进行对比,当R=5时,新密码S盒的最优差分特征(线性逼近)的概率为2-17(2-8),而Alzette最优差分特征(线性逼近)概率为2-10>2-17(2-5>2-8);R=6时,新密码S盒的最优差分特征概率为2-17,而此时Alzette最优差分特征概率为2-16>2-17;R=7时,新密码S盒的最优线性逼近概率为2-17,而此时Alzette最优线性逼近概率为2-13>2-17。由此可见,与Alzette相比,新密码S盒在第5轮就能够更好地抵抗差分密码分析和线性密码分析,在第6轮和第7轮抵抗差分密码分析和线性密码分析的能力更出色。 表5 结果对比 笔者基于ARX结构,设计了一种64 bit的大状态轻量级密码S盒。针对循环移位量的选取,首先对候选方案进行分类,然后采用“层次筛选法”,结合MILP技术构建差分/线性密码分析的自动化分析模型,最终搜索到2种最佳的候选方案。此外,在自动化分析模型中,通过调用“回调函数”来优化模型,将目标最优值不满足给定条件的模型提前终止,大大缩短了运行时间,提高了搜索效率。新密码S盒与文献[10]的Alzette所需的软硬件实现成本相当;在安全性分析方面,新密码S盒在迭代5轮后比Alzette抗差分密码分析和线性密码分析的能力更强;随着迭代轮数的增加,其抵抗差分/线性密码分析的能力可以达到更高的水平。3 基于MILP面向ARX密码算法的差分/线性分析模型
3.1 差分特征的自动化搜索模型

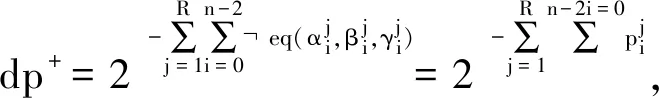
3.2 线性逼近的自动化搜索模型
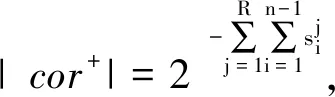
4 新密码S盒的设计与安全性分析
4.1 新密码S盒的设计



4.2 新密码S盒的安全性分析



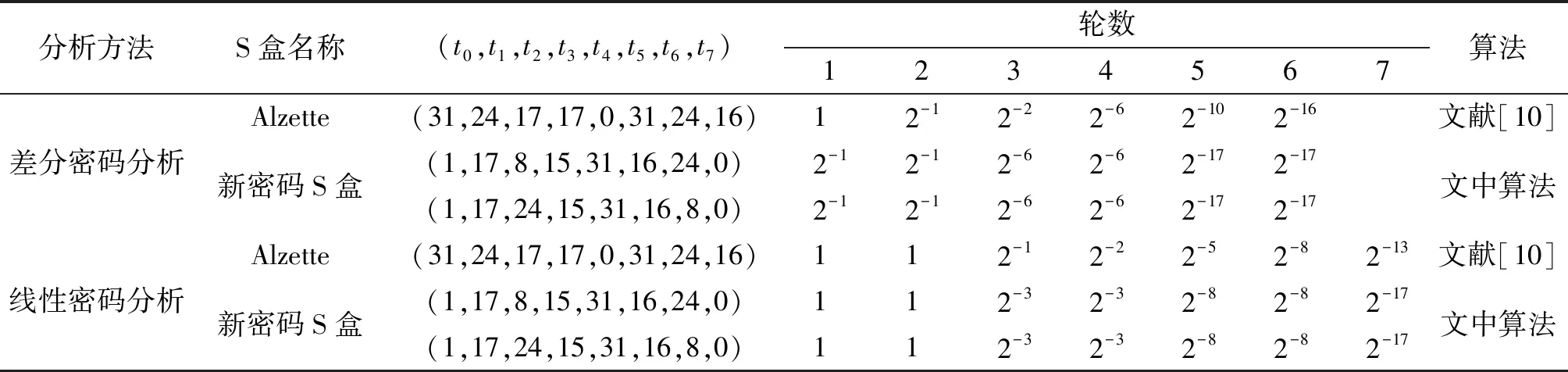
4.3 结果对比
5 结束语

