自适应裁剪的差分隐私联邦学习框架

王方伟,谢美云,李青茹,王长广

(河北师范大学 计算机与网络空间安全学院 河北省网络与信息安全重点实验室,河北 石家庄 050024)

1 引 言

信息化时代,各种智能设备及应用每天都会产生海量数据。机器学习,尤其是深度学习,为充分挖掘数据价值提供了一件有力武器,已在计算机视觉、语音识别、自然语言处理等领域取得巨大成功。然而,频发的隐私泄露事件引发了民众对于数据隐私和安全的担忧,越来越多的组织和公司不愿共享自己的数据,出现“数据孤岛”问题。联邦学习是一种分布式机器学习模式,参与模型训练的各方不会交换彼此数据。各参与方在本地完成数据存储和模型训练,只需将相关训练参数上传至中央服务器,由中央服务器统一维护全局参数的更新[1]。联邦学习在不共享数据的前提下由多方协作共同训练一个深度学习模型,降低了隐私泄露风险,极大释放了数据价值,可有效缓解“数据孤岛”问题。

尽管联邦学习对保护数据隐私有一定作用,但客户端频繁上传和下载参数,仍然存在隐私泄露的风险[2]。如何设计满足隐私要求的联邦学习方案仍是一个挑战。研究者尝试将安全多方计算、同态加密和差分隐私等数据安全技术结合联邦学习,提出一些联邦学习隐私保护框架[3-7]。KANAGAVELU等[4]提出高效通信的多方计算支持的联邦学习(Communication-Efficient multi-party computation enabled Federated learning,CE-Fed)算法,实现了高精度、高通信效率的联邦学习。MA等[5]提出基于多密钥同态加密技术的联邦学习,旨在实现隐私保护的联邦学习,并降低计算成本。PARK等[6]利用同态加密技术直接对模型参数进行加密,中央服务器直接对密文进行计算而无需解密。张泽辉等[7]提出一种支持数据隐私保护的联邦深度神经网络模型(Privacy-preserving Federated Deep Neural Network,PFDNN),通过对其权重参数实施同态加密来保障数据的隐私安全。然而,安全多方计算大多基于复杂的通信协议,同态加密涉及大量加密操作,尽管可实现数据的“可算而不可见”,但也为系统带来了巨大的计算开销和通信开销。与安全多方计算和同态加密不同,差分隐私因其实现的简单性和强大的隐私性而受到关注,已应用到多个领域以提升系统的隐私性[8]。

差分隐私应用于联邦学习有两种方式,即本地化差分隐私(Local Differential Private,LDP)和中心化差分隐私(Centralized Differential Private,CDP)[9]。本地化差分隐私首先使得数据拥有者完全掌握对数据的控制权,在本地对数据进行干扰,然后向服务器发送扰动后的版本,从而防止了数据的隐私泄露。TRUEX等[10]提出了本地差分隐私的联邦学习(Local Differential Private Federated learning,LDP-Fed)算法,首先根据本地需求定制隐私预算,然后在本地对模型参数进行基于本地化差分隐私的扰动。SUN等[11]考虑深度学习模型的不同层的权重范围差异,提出了一个权重参数自适应范围设置方法及数据扰动方法,提升了模型性能。 ZHAO等[12]设计了一种适应于本地化差分稳私的联邦随机梯度下降(Federated Stochasitc Gradient Desent,FedSGD)算法,既可实现对梯度的扰动,提升模型精度,又能减少通信成本。CHAMIKAPA等[13]提出了LDPFL(Local Differential Privacy for Federated Learning)算法,通过随机化本地模型的输入来实现本地化差分稳私,训练的模型在保持高精度的情况下,隐私泄露更少。ZHAO等[14]提出了一种增强联邦学习框架,通过客户端自采样和自适应数据扰动机制实现本地化差分稳私。相比于中心化差分稳私,本地化差分稳私能提供更高的隐私水平,但会引入更多噪声,从而影响模型精度。另外,本地化差分稳私不利于处理高维、稀疏数据。

中心化差分隐私主要针对客户—服务器架构,对服务器获取和广播的参数提供隐私保护。为了解决隐私性与模型效用之间的权衡问题,LIU等[15]提出了自适应隐私保护的联邦学习(Adaptive Privacy-preserving Federated Learning,APFL)算法,首先使用相关性传播算法计算每个数据属性类对输出的贡献度,然后向数据属性中注入自适应噪声。WU等[16]在客户端执行本地梯度下降的过程中引入自适应学习率调整算法,提升了计算效率,并利用差分隐私有效抵御了各种背景攻击。朱建明等[17]根据各参与方的模型质量评估结果,为中间参数添加不同程度的噪声,从而保证本地数据的隐私安全。HU等[18]开发了一种稀疏模型扰动的联邦学习(Federated learning with Sparsified Model Perturbation,Fed-SMP)方案,通过模型稀疏化技术实现了隐私保护水平和通信效率的提高。LIU等[19]设计了一种自适应梯度裁剪的差分隐私联邦学习算法,根据用户的梯度信息来动态调整每个通信轮次中的梯度裁剪阈值,减少了因裁剪阈值设置不合理对模型精度的影响。SHEN等[20]提出了性能增强的差分私联邦学习(Performance-Enhanced Differential Privacy-based Federated Learning,PEDPFL)算法,使用正则化提升模型的鲁棒性。LIAN 等[21]提出了基于层的联邦学习(Layer-Based Federated Learning,Layer-Based FL)算法,通过比较本地模型与全局模型的相关性,在本地选择部分模型参数进行扰动后上传给服务器,以此来减少通信中的负载。BAEK等[22]针对联邦学习中的用户掉线问题,提出了一种对用户掉线且具有鲁棒性的差分稳私机制,减少了因用户意外掉线而造成的隐私预算过度消耗。

中心化差分隐私在应用中仍面临隐私性与模型精度之间的权衡;另外,在实现中心化差分隐私时,要求服务器是可信的,噪声由服务器添加,一旦服务器忽略了噪声的添加,就会导致隐私泄露风险。针对以上问题,文中提出了自适应裁剪的差分隐私联邦学习框架,首先将噪声添加操作由服务器转移至本地,各客户端完成本地更新后,向更新的模型参数中添加自适应噪声,然后将加噪后的模型参数上传至服务器,执行全局模型参数更新,保障了参数传输期间的数据隐私安全。

2 预备知识

2.1 联邦学习

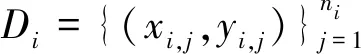
(1)

其中,Fi(ω)表示客户端i计算得到的损失函数。

2.2 差分隐私

差分隐私的核心思想是通过向统计结果中添加噪声,使数据集中某一条记录的改变不会显著影响算法的结果,从而保护数据的隐私。其定义如下:

定义1((ε,δ)差分隐私[24]) 令M:D→R为随机算法,d∈D,d′∈D为最多相差一条记录的相邻数据集,若算法M在d和d′上任意输出结果O∈R都满足式(2),则称算法M实现(ε,δ)差分隐私。

Pr[M(d)=O]≤eε×Pr[M(d′)=O]+δ,

(2)

其中,参数ε表示隐私保护预算,反映了算法的隐私保护程度,且ε越小,隐私保护程度越高。δ是松弛项,表示违背纯ε差分隐私的概率。

定义2(全局灵敏度[24]) 对于任意查询函数f：D→Rd,其敏感度为

(3)

其中,d和d′为最多相差1条记录的相邻数据集。敏感度可衡量改变数据集中任意一条记录对于f的输出造成的最大影响,它决定了为实现差分隐私,需要向f的输出结果中添加的噪声量。

实现差分隐私的一种典型机制为高斯机制,通过向输出结果中添加服从高斯分布的噪声Y～N(0,(Δf)2σ2)来实现,σ为噪声乘子,且σ≥(2ln(1.25/δ)1/2/ε。

差分隐私作为一种鲁棒模型,具有如下性质:

性质1(后处理免疫性[24]) 对于同一数据集D,若算法M满足(ε,δ)差分隐私,则对于任意随机算法A(不一定满足差分隐私),新的算法M′=A(M(D))仍满足(ε,δ)差分隐私。

性质2(序列组合性[25]) 假设算法M1(D),M2(D),…,Mk(D)均满足(ε,δ)差分隐私,则对于同一数据集D,由这些算法构成的组合算法Φ(M1,M2,…,Mk)满足(ε,δ)差分隐私保护。

3 自适应差分隐私联邦学习框架

联邦学习作为一种分布式机器学习模式,各参与者与服务器之间的频繁通信使得联邦学习面临着巨大的计算和通信开销。相比传统的密码学技术,差分隐私具有成本低、算法简单、且能够提供强大隐私保障的特点,将差分隐私应用于联邦学习时并不会增加过多的计算和通信开销,但在实现时引入的噪声不可避免地会对模型性能产生影响。如何在隐私性与模型性能之间取得良好的权衡,成为差分隐私更好地部署于联邦学习中的关键。文中从差分隐私部署的关键步骤(梯度裁剪)出发,提出一个自适应差分隐私联邦学习框架(Adaptive Differential Privacy Federated Learning,ADP_FL),采用高斯机制实现差分隐私保护。在该框架中,客户端与服务器的通信过程如图1所示。

图1 自适应差分隐私联邦学习框架示意图

3.1 自适应裁剪阈值

在差分隐私设置中,梯度裁剪至关重要,可有效防止因个别梯度过大对模型更新产生的影响。梯度裁剪阈值作为一个超参数,需要用户仔细选择。若梯度裁剪阈值设置过大,则会引入过多不必要的噪声,从而影响模型性能;若梯度裁剪阈值设置过小,则会损失过多的梯度信息。梯度裁剪主要有两种形式:①基于数值的裁剪,即梯度向量的各个值大于预设的阈值则被裁剪;②基于范数的裁剪,即梯度范数大于预设阈值则被裁剪。相比基于数值的裁剪,基于范数的裁剪实现了对梯度向量的缩放,能更多地保留梯度中的信息。目前广泛使用的是基于范数的裁剪,这也是文中研究的内容。针对梯度裁剪阈值的设置问题,提出了一种自适应裁剪阈值选取(Adaptive Dlipping threshold selection,Ada_Clip)算法,具体为:计算每个迭代中梯度的L2范数,选取历史梯度L2范数的p百分位数,作为当前迭代的裁剪阈值,即

Ct=[G0,G1,…,Gt]p,t≥0 ,

(4)

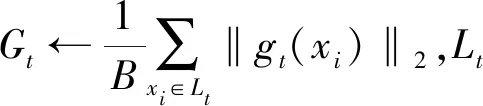
在自适应裁剪阈值选取算法中,较高的p值将导致较少的裁剪被应用到梯度上。若p=100,则在模型训练期间梯度不会被裁剪;若p=0,则在每次迭代中梯度都会被裁剪到训练过程中梯度的最小值。自适应裁剪阈值选取算法根据历史梯度的变化趋势,来预测当前迭代中梯度的变化,以便给出一个合理的限制,用户只需要确定裁剪的百分比即可。百分数的引入也能够更好地隐藏原始梯度信息。

每个训练批次中的每个数据的梯度都将被裁剪,取该批次中所有梯度裁剪后的值再求平均,作为该次迭代中的梯度,即

(5)

算法1自适应差分隐私联邦学习框架。

输出:模型参数ωT

① fort=0,1,…,T-1 do

② for 每一客户端k∈Stdo

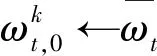
④ fore=1,2,…,Edo

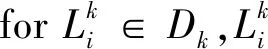
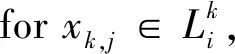
3.2 框架详细设计

为防止联邦学习中客户端数据隐私的泄露,结合自适应裁剪阈值选取策略,提出了一种自适应差分隐私联邦学习框架(ADP-FL),如算法1所示。该框架包含4个主要步骤。

步骤1 本地训练。为减少与服务器的通信次数,参与模型训练的各客户端在可本地执行多次梯度下降,并对每次迭代中计算的梯度进行裁剪,梯度裁剪阈值由自适应裁剪阈值选取算法来确定。各客户端可以自主选取梯度裁剪的百分比,文中各客户端的裁剪百分比是相同的。梯度裁剪操作旨在限制梯度的范围,方便后续添加噪声。

步骤2 参数上传。为防止客户端数据隐私泄露,各客户端将自己在本地训练得到的模型参数上传至服务器之前,需要向本地更新的模型参数中添加自适应的高斯噪声,即

(6)

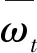
步骤3 参数聚合。每一轮选择K个客户端,而非所有客户端参与模型聚合,通信中聚合的全局模型参数为

(7)

步骤4 参数广播。服务器不重复地随机选择一个客户端子集,将更新后的模型参数广播至各客户端。服务器无需访问本地数据信息。每个客户端下载服务器提供的全局模型,来更新自己的模型。另外,每一个客户端与服务器进行通信,都需要消耗一定的通信成本。在参数广播时,服务器选择部分客户端,而非全部客户端进行参数广播,在一定程度上可减少通信成本。

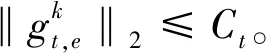
(8)

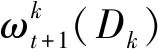
(9)

根据引理1,每个参与模型聚合的客户端需要添加在上传参数中的噪声标准差为2ηtECtσt/B。

3.3 隐私性分析

定理1记总通信轮次为T,对于任意客户端i的本地数据集Di,算法1满足(Tε,Tδ)差分隐私。

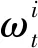
4 实验结果与分析

4.1 实验设置

实验采用两种公开数据集。

(1) Fashion-MNIST:包含70 000张10类服饰的灰度图片,每张图片大小为28×28像素,训练集包含60 000张图片,测试集包含10 000张图片。

(2) CIFAR10:包含10种类型的彩色图片,标签为飞机、汽车、鸟、猫、鹿、狗、青蛙、马、船、卡车,每张图片大小为32×32像素,训练集包含50 000张图片,测试集包含10 000张图片。

对于Fashion-MNIST数据集,网络结构由1个包含256个神经元的全连接层组成。对于CIFAR10数据集,采用两种网络结构,模型1是包含两个卷积层和两个全连接层的网络,两个卷积层使用的卷积核大小都是5×5,输出通道数分别为64和128,全连接层包含的神经元分别为384个和192个;模型2采用VGG16网络。3个网络均采用SoftMax函数实现网络输出,并使用交叉熵计算损失函数。文中实验中的客户端数量均设置为50个,实验使用PyTorch框架在 NVIDIA GeForce RTX 2080 Ti服务器上运行,结果均取5次测试的平均值,结果的方差标注在表1和表2中。

表1 在数据集Fashion-MNIST和CIFAR10上的结果(模型精度) %

表2 在数据集CIFAR10上使用VGG16在不同隐私预算下的结果(模型精度) %

4.2 性能评估

4.2.1 算法有效性评估

为验证所提算法的有效性,设计实验将自适应差分隐私联邦学习算法与客户端级的差分隐私联邦学习(Client-level Differential Privacy Federated Learning,CDP_FL)算法[15]、使用固定噪声的差分隐私联邦学习(Differential Privacy Federated Learning,DP-FL)算法[16]和未经差分隐私保护的联邦学习(Non-Differential Privacy federated learning,No_DP)算法[1]进行比较,结果如表1所示,模型精度一律采用百分数表示。实验结果表明,所提出的自适应差分隐私联邦学习框架能够在保证数据隐私的前提下,提升模型精度。另外,在不同隐私水平下的实验结果表明,隐私预算越高,所提方法对于模型精度的提升越明显。文中还进一步尝试使用更复杂的网络来验证提出方法的有效性,结果如表2所示。在隐私预算ε=6.0时,模型精度与非隐私情况相比,相差2.06%;相同隐私预算下,更复杂的网络对于模型提升是有益的。值得注意的是,本实验中的隐私预算均指模型在训练期间消耗的总体隐私预算。

图2展示了Fashion-MNIST在隐私预算ε=0.5时模型精度随通信轮次的变化,图3展示了CIFAR10使用模型1在隐私预算ε=4.0时模型精度随通信轮次的变化。从两个数据集上的实验结果表明,未经差分隐私保护的联邦学习算法在不同的学习任务上始终保持最高的模型精度,且训练过程也更加稳定,这说明噪声的引入会导致模型收敛过程中的波动,也会对模型精度产生一定程度的影响。另外,改变添加噪声的规模对于模型精度和收敛性能的提升都是有益的。相比中心化差分隐私保护算法,文中提出的自适应差分隐私联邦学习算法从自适应裁剪阈值选取维度来间接影响添加的噪声规模,在提升模型精度的同时,也使训练更加稳定。

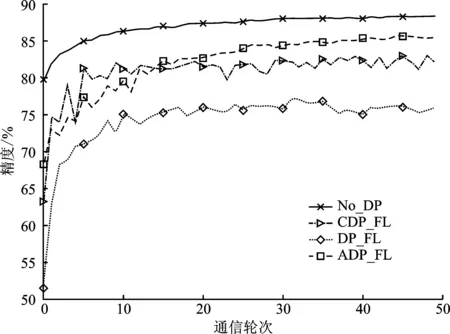
图2 在Fashion-MNIST上不同算法的训练精度随通信轮次的变化

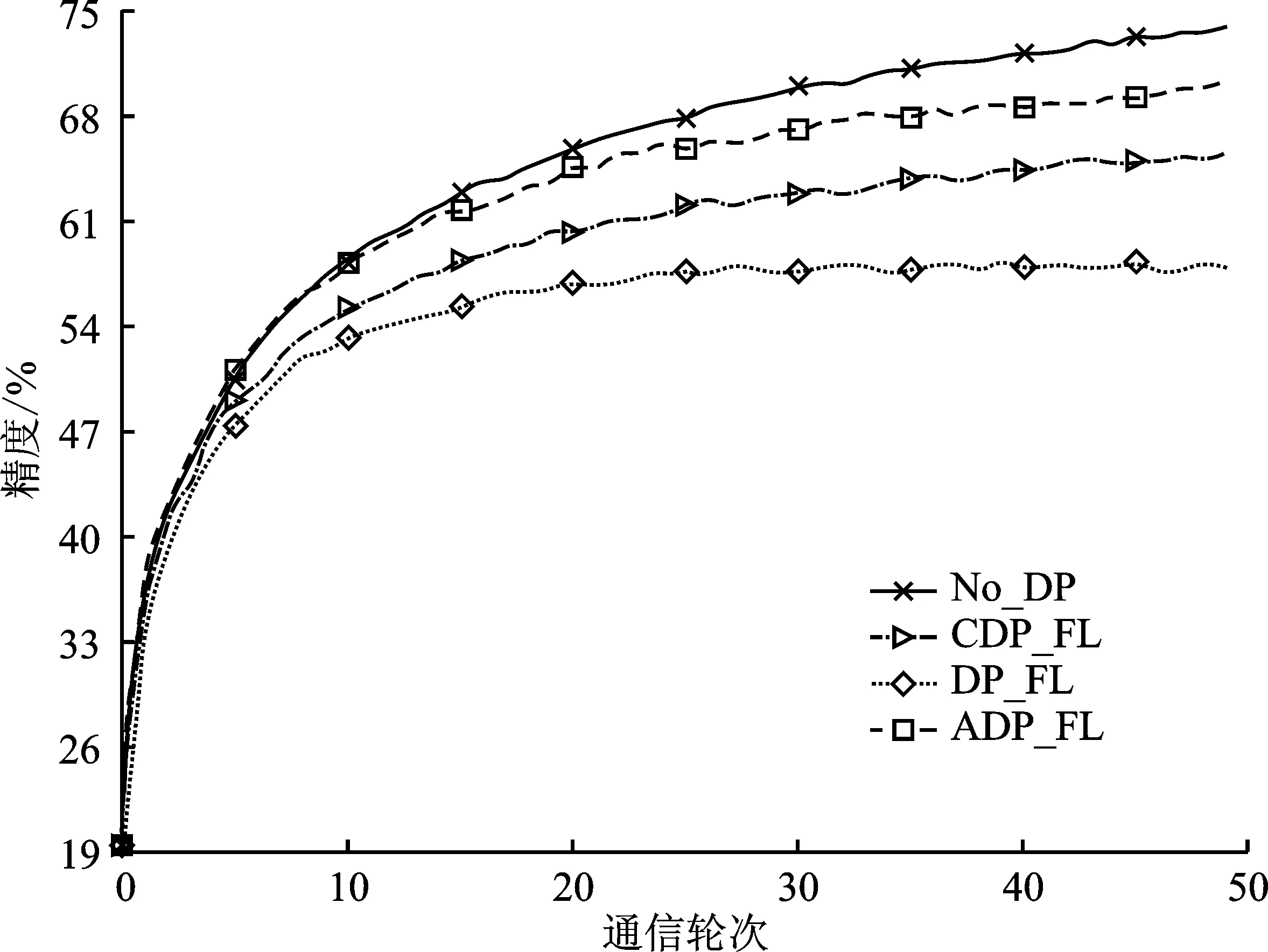
图3 在CIFAR10上(模型1)不同算法的训练精度随通信轮次的变化

此外,将ADP_FL与Layer-Based FL[24]做了比较,在两个数据集上均进行50轮通信,实验结果如表3所示。在该实验中,用客户端与服务器之间的通信轮次来衡量通信成本。两种方法在相同通信成本下,实现了相似的模型精度,说明ADP_FL能够提供更强的隐私保障。

表3 算法有效性比较(模型精度) %

4.2.2 本地迭代次数的影响

对于Fashion-MNIST和CIFAR10这两个数据集,选取本地迭代次数都为E={2,3,5,7},隐私预算分别为ε=0.5和ε=4.0。图4～6给出了在无隐私(No_DP)和使用所提方法(ADP_FL)的情况下,本地迭代次数对模型精度的影响。对于无隐私的情况,本地运行更多迭代能够使全局模型收敛更快,有益于模型精度的提升;但对于添加噪声的情况,更多迭代将导致模型精度的降低。原因是本地迭代次数与敏感度有关,更多的本地迭代次数将导致敏感度成倍的增加,进而增大添加的噪声规模,从而导致模型精度逐渐降低。另外,由图4～6也可以看出,对于给定的隐私水平,存在一个较优的本地迭代次数,能够在保证隐私的同时,维持模型较高的精度。

图4 在Fashion-MNIST上本地迭代次数对模型精度的影响

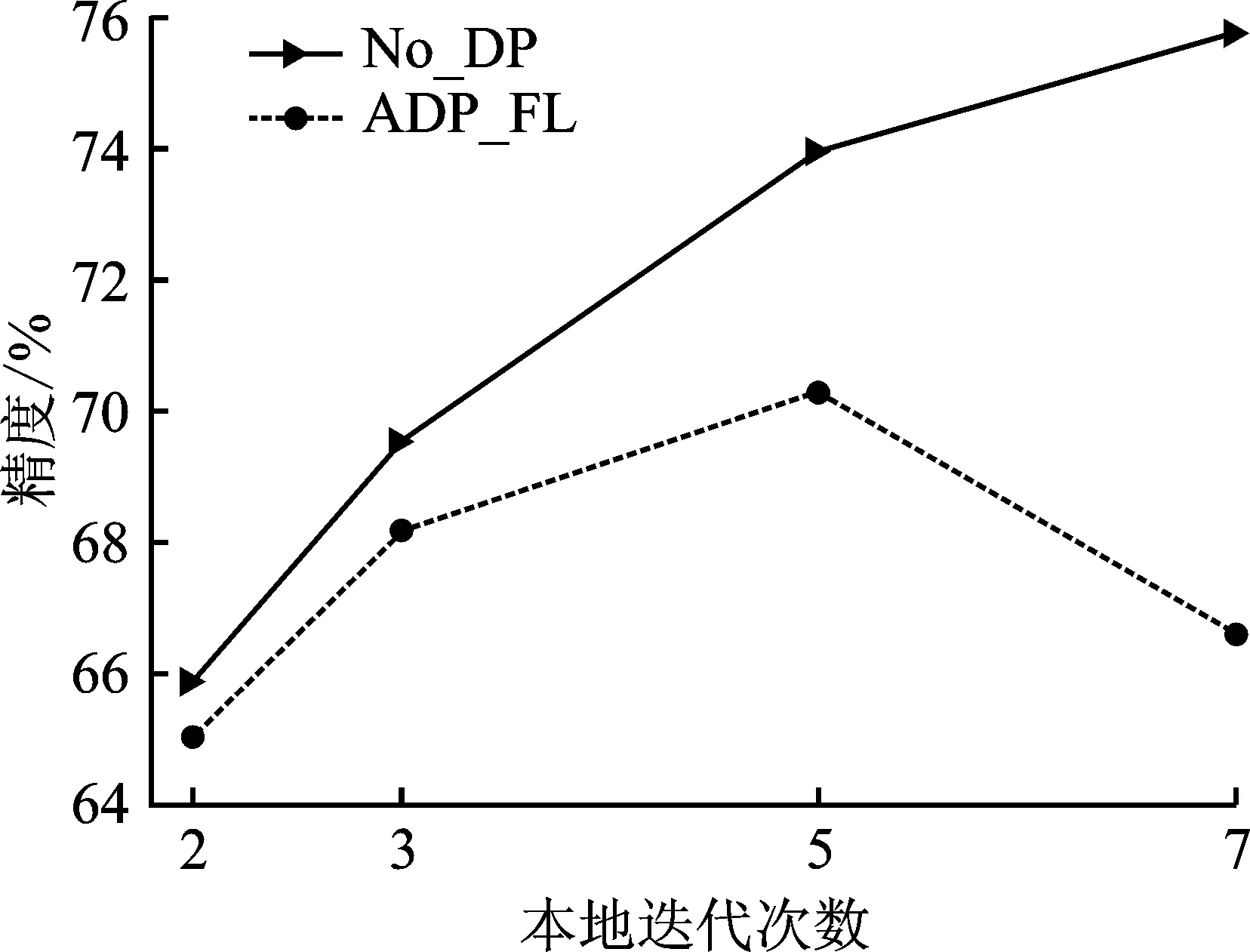
图5 在CIFAR10上(模型1)本地迭代次数对模型精度的影响

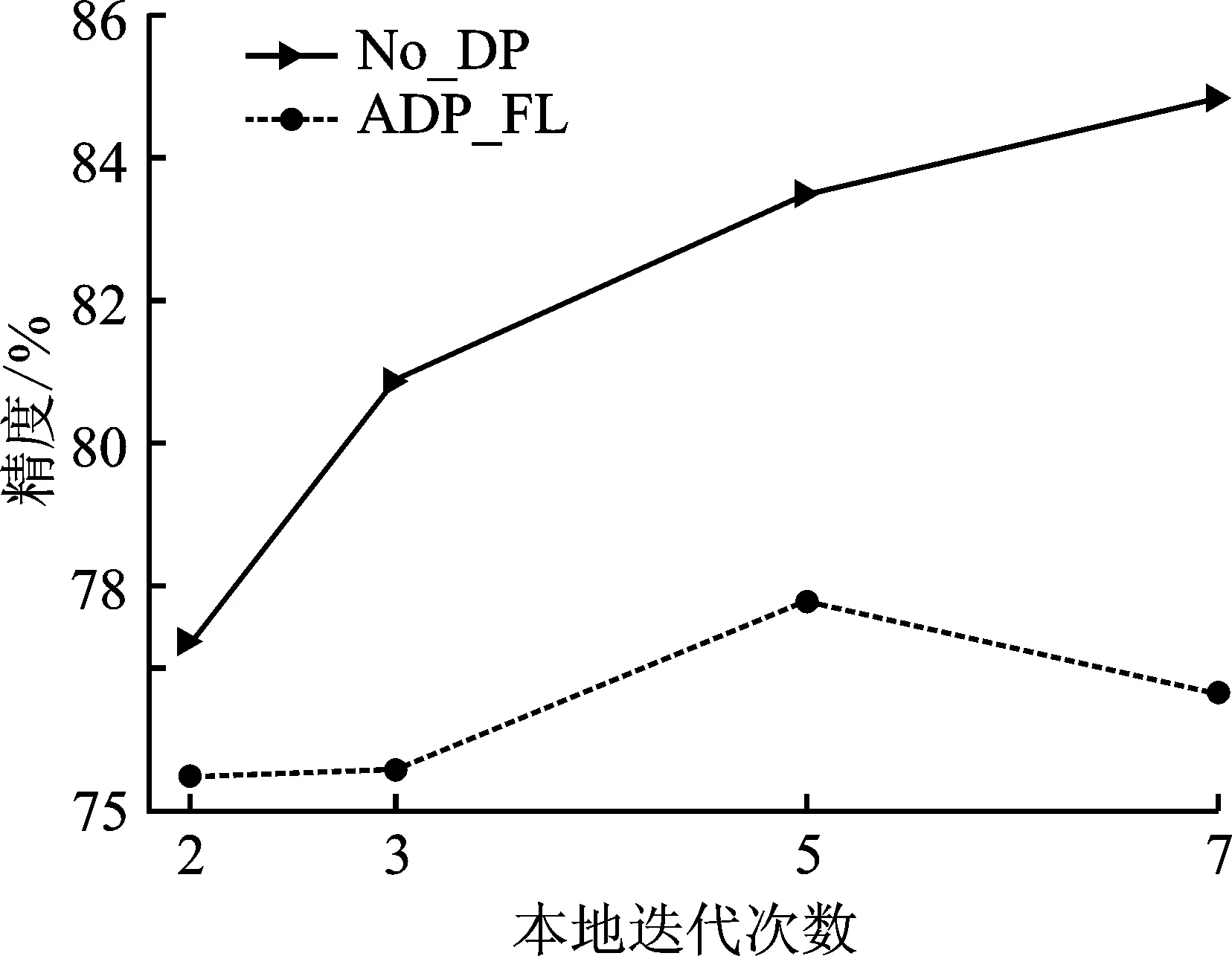
图6 在CIFAR10上(模型2)本地迭代次数对模型精度的影响

4.2.3 裁剪百分比大小的影响

对于Fashion-MNIST和CIFAR10这两个数据集,选取本地迭代次数都为E=5,隐私预算分别为ε=0.5和ε=4.0。由图7～9可以看出,裁剪百分比与模型精度成反比,即裁剪百分比越大,模型精度反而越低。这主要是因为裁剪阈值与敏感度有关,尽管较大的裁剪阈值能够更多地保留梯度当中的信息,但同时也会引入过多的噪声,导致模型精度降低。

图7 在Fashion-MNIST上裁剪百分比对模型精度的影响

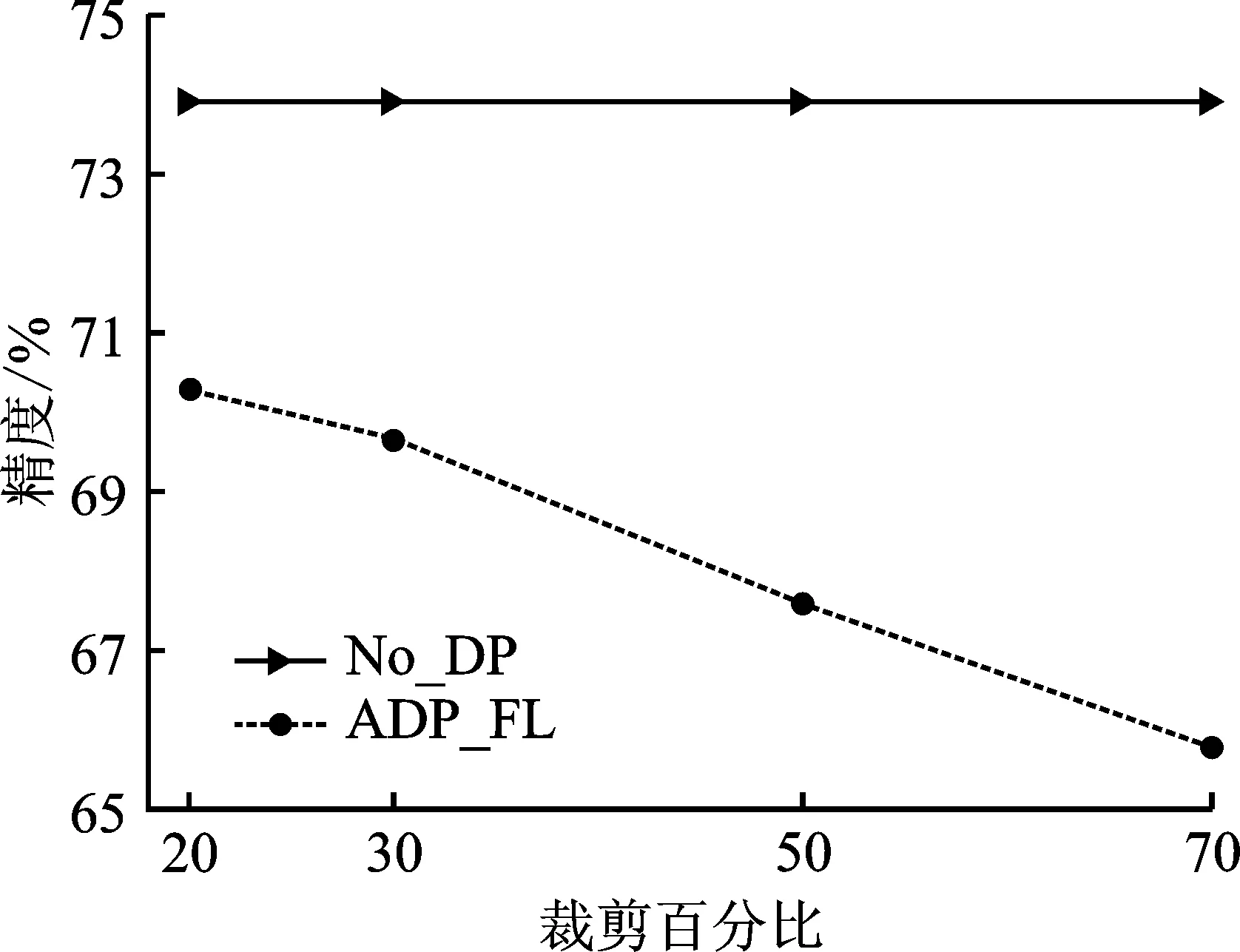
图8 在CIFAR10上(模型1)裁剪百分比对模型精度的影响

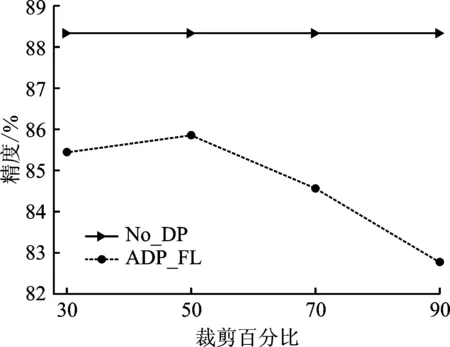
图9 在CIFAR10上(模型2)裁剪百分比对模型精度的影响

5 结束语

笔者重点关注差分隐私在联邦学习中的部署,设计了一种基于自适应差分隐私的联邦学习框架。在本地模型训练期间,客户端可在本地执行多次迭代,通过自适应裁剪阈值选取策略在每个迭代中对梯度裁剪阈值进行校准,仅在参数上传时在本地完成自适应噪声的添加。通过在Fashion-MNIST和CIFAR10两个数据集上的实验结果表明,该算法在为数据的隐私和安全提供强大隐私保证的同时,提升了模型性能,也使模型的训练过程更加稳定。另外,从理论上分析了本地执行梯度下降的次数和本地训练批次大小对模型性能的影响,并通过实验加以验证。

文中的隐私预算采用平均分配的策略,这样会造成不必要的隐私预算浪费,下一步将结合更加精准的隐私损失度量方法,对迭代过程中消耗的隐私预算实现更加精准的追踪。另外,由于数据采样方法的差异,联邦学习中参与训练的各客户端数据存在异构性问题。下一步将研究各客户端数据异构的场景下,差分隐私如何更好地部署在联邦学习中。