自适应差分隐私的高效深度学习方案
王玉画,高 胜,朱建明,黄 晨
(中央财经大学 信息学院,北京 100081)
1 引 言
近年来,深度学习技术作为机器学习研究的前沿领域,凭借对文本、声音、图像等数据的强大处理和理解能力,在社会网络分析、物联网和无线通信等诸多领域任务中表现出优越的性能。其巨大成功主要依赖于高性能的计算、大规模的数据以及各种深度学习框架的开源。深度学习技术主要分为两个阶段:首先是模型训练阶段,用收集到的海量数据对深度神经网络模型进行迭代训练,直到模型收敛,获得目标模型;其次是模型推理阶段,利用训练好的目标模型对目标数据集执行分类和预测等任务。
然而,由于攻击手段的不断演进,深度学习模型存在的隐私泄露风险也随之增加。常见的攻击方式有模型反演攻击和成员推理攻击。模型反演攻击在模型训练和推理阶段都可能发生,敌手通过截取模型参数和测试模型输出来重建训练数据集。SONG等[1]根据模型参数重构原始的训练数据,窃取特定个体数据的敏感信息。成员推理攻击主要发生在模型推理阶段,敌手通过目标模型的输出差异来推断给定样本是否属于模型的训练集[2]。SALEM等[3]证明了敌手可以在没有任何背景信息的情况下,根据目标模型的输出规律判断出样本是否参与过训练。本质上,这些隐私问题的产生归因于深度神经网络独特的学习和训练方法,通过大量的隐藏层不断提取高维数据特征,模型将记住某些数据细节,甚至整个数据集[4]。
针对深度学习潜在的隐私威胁,现有的方案通过结合一些经典的隐私保护机制来增强隐私,主要分为加密机制和扰动机制[5]。加密机制目的在于保护数据交换的过程,常用同态加密和安全多方计算实现。其中,同态加密允许第三方无需解密就可以直接在加密域上执行计算,保证了模型参数的精度[6-7];安全多方计算允许当不可信多方参与到模型的训练和推理过程时,通过秘密共享或不经意传输等来实现数据的安全性[8-9]。相比于同态加密方法,基于安全多方计算的方案虽然不需要大量计算开销,但却增加了通信成本。扰动机制目的在于保护数据内容本身,通过差分隐私(Differential Privacy,DP)[10]技术在模型训练过程中添加噪声来扰动,使得某条数据是否参与训练对最终的输出结果影响微乎其微。这是一种轻量级隐私保护技术,计算效率高,通信开销低,且具有后处理性。基于差分隐私的方案关键在于模型效用和隐私保护之间的权衡[11-15]。ABADI等[16]设计了一种差分隐私随机梯度下降(Differential Private Stochastic Gradient Descent,DPSGD)算法,将多个数据批分为一组,对每组的累积梯度添加噪声,还引入矩会计 (Moment Accountant,MA) 来追踪隐私损失,从而获得更紧致的整体隐私损失估计。然而,该算法以等量的隐私预算加噪会导致原始梯度出现较大失真,数据可用性显著降低。ZHANG等[17]提出了一种自适应衰减噪声的隐私保护算法,每次迭代中向梯度加入通过线性衰减率调整的噪声,以减少负噪声的添加,但此方案对于线性衰减率并没有很好的计算方法,只能通过实验调试,实用性较差。所提两种方案都是对梯度进行二范数裁剪来控制梯度的敏感度,可实际应用中对高维梯度的裁剪范围较难把握,且每轮训练中每个批次的迭代都需要加噪,使得隐私损失严重依赖于迭代次数,当需要较多次迭代来保证模型准确性时,其训练效果会受到影响。PHAN等[18]提出了一种自适应拉普拉斯机制,通过逐层相关传播 (Layer-wise Relevance Propagation,LRP) 算法衡量深度神经网络中输入与输出的相关性,再根据相关性对第一个隐藏层加入拉普拉斯噪声,真正实现了从样本特征的角度来自适应确定噪声大小。可是,在使用LRP算法时可能会泄露隐私。作为改进,ZHANG等[19]设计了一种自适应动态隐私预算分配的差分隐私方案(Adaptive allocation Dynamic privacy budget Differential Privacy,ADDP),对LRP算法输出的相关性进行了加噪处理。LIU等[20]引入随机化隐私保护调整技术,直接对相关性超过设定阈值的输入特征进行扰动,未超过阈值的特征由随机因子决定是否被扰动。然而,不同预定阈值和随机因子的选取会对模型效用造成不同的影响。以上三种方案都采用拉普拉斯机制加噪太过严格,且没有很好地考虑相关性衡量算法与数据可用性之间的关系,较精确的相关性衡量才能获得较好的数据可用性。更多地,这三种方案都没有在设计时兼顾到模型的收敛速度,而在实际应用中这也是非常重要的。
为解决现有深度学习差分隐私保护方案中所存在的迭代与隐私预算之间依赖、数据可用性较低和收敛速度较慢等问题,笔者提出了一种自适应差分隐私的高效深度学习(Adaptive Differential Privacy-based Efficient deep learning,ADPE) 方案。主要贡献如下。
(1) 设计一种自适应差分隐私机制,通过Shapley加性解释模型在特征维度对原始样本进行自适应扰动,使得迭代次数独立于隐私预算,并结合函数机制来保护样本的真实标签,从而实现对原始样本及其标签提供隐私保护的同时,保证数据的可用性。
(2) 将自适应矩估计算法与指数衰减函数相结合,利用先验知识优化梯度,针对不同的参数调整学习率,加快模型收敛速度,并增强后期模型训练的稳定性。
(3) 引入零集中差分隐私中的组合机制对整个方案的隐私损失进行更清晰更紧凑的统计,从而降低因隐私损失超过隐私预算带来的隐私泄露风险,更好地平衡隐私和效用之间的关系。
(4) 给出了详细的隐私分析,并在MNIST和Fashion-MNIST数据集上通过衡量模型的分类准确率进行了对比实验。与其他方案相比,文中所提方案效果更优。
2 预备知识
2.1 差分隐私
差分隐私的提出是为了解决查询数据库中的隐私信息泄露问题,其主要基于扰动的思想,让敌手无法根据查询结果来判断出单条数据记录的更改或增删,即输出结果对于数据集中的任何一条特定记录都不敏感。差分隐私的形式化定义如下。
定义1(ε,δ)-DP[10]。设有隐私机制M,其定义域为Dom(M),值域为Ran(M)。若隐私机制M对于任意两个仅相差一条记录的相邻数据集D和D′⊆Dom(M),O⊆Ran(M),满足:
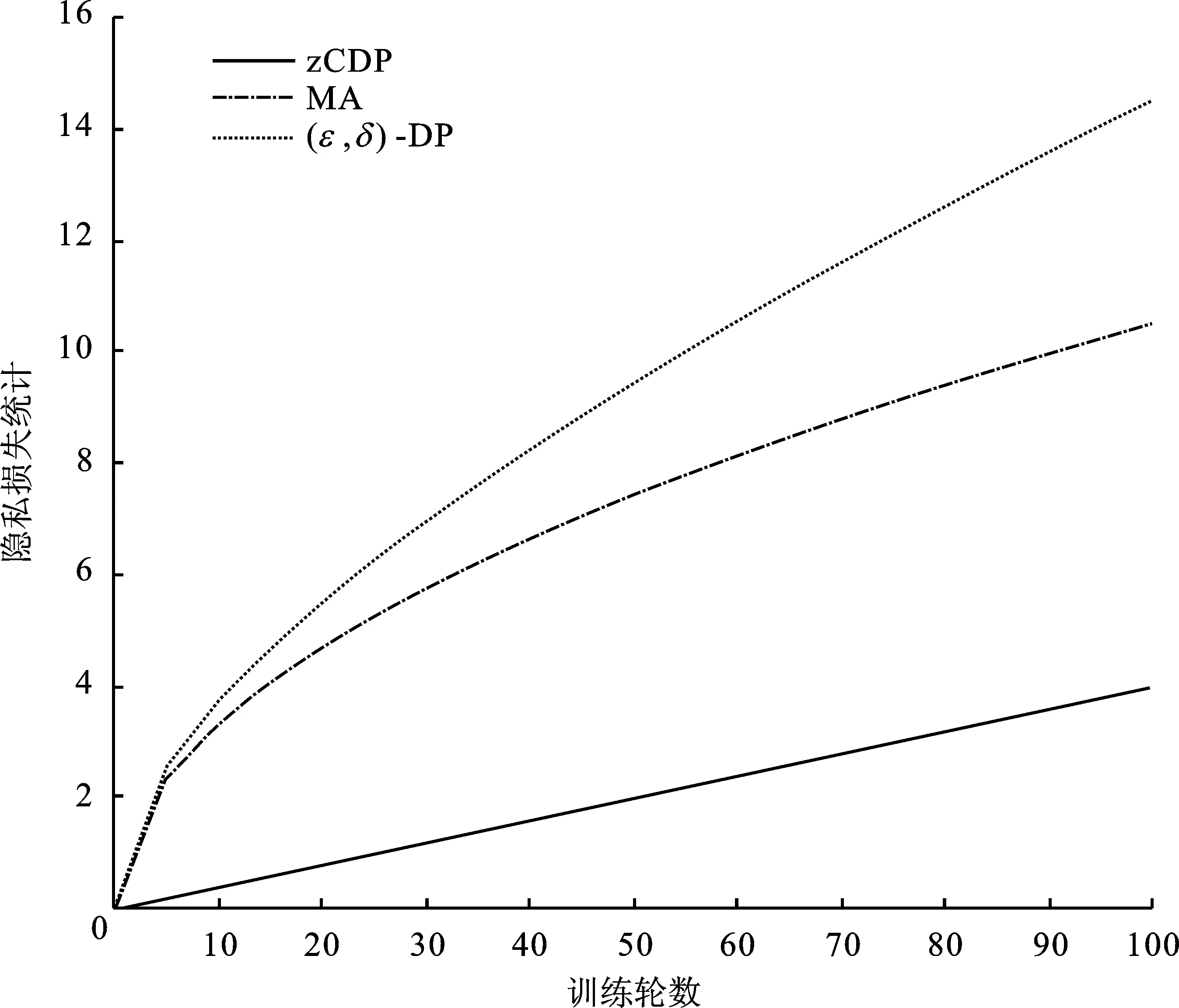
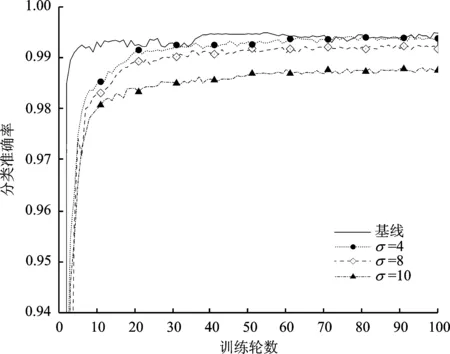
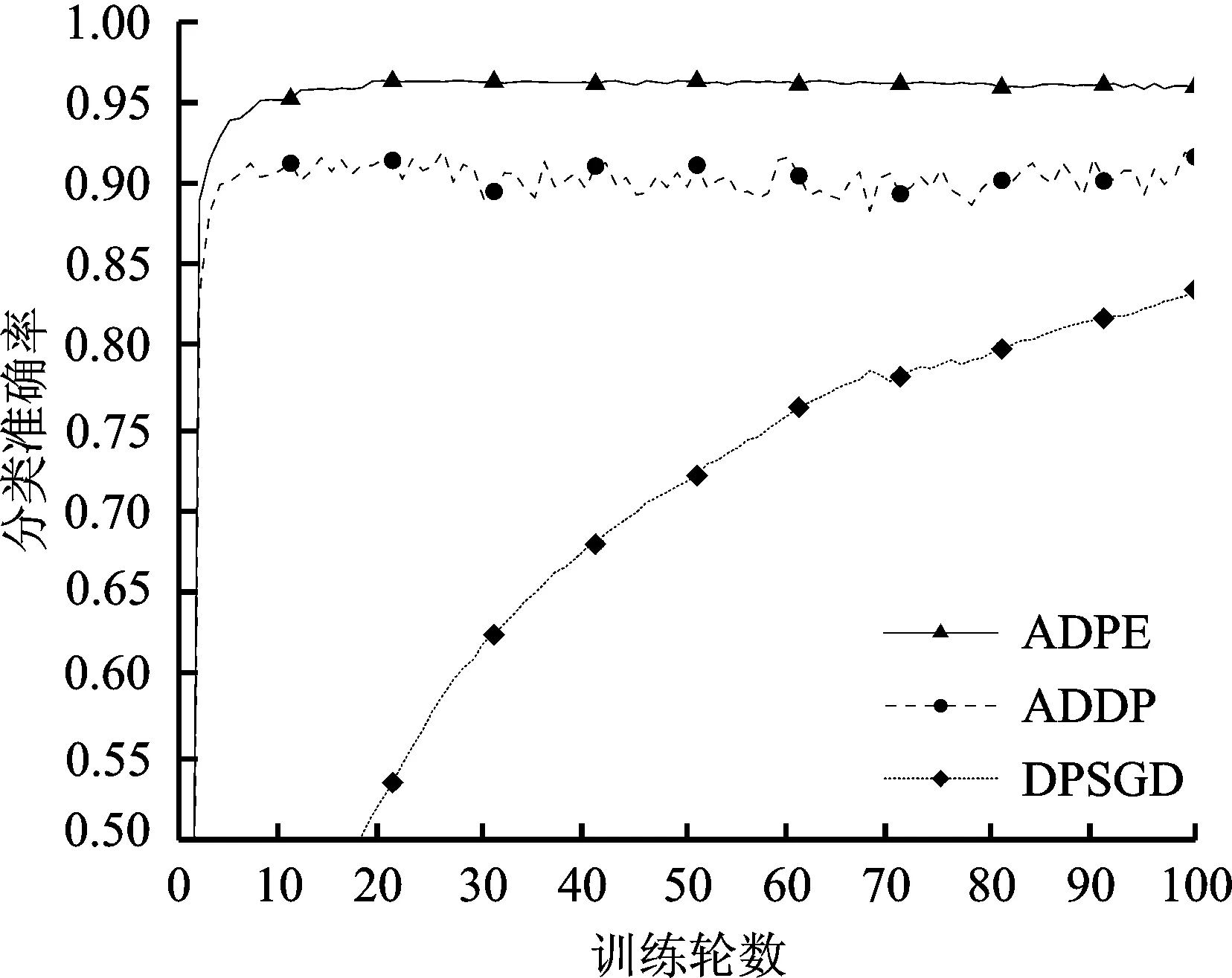
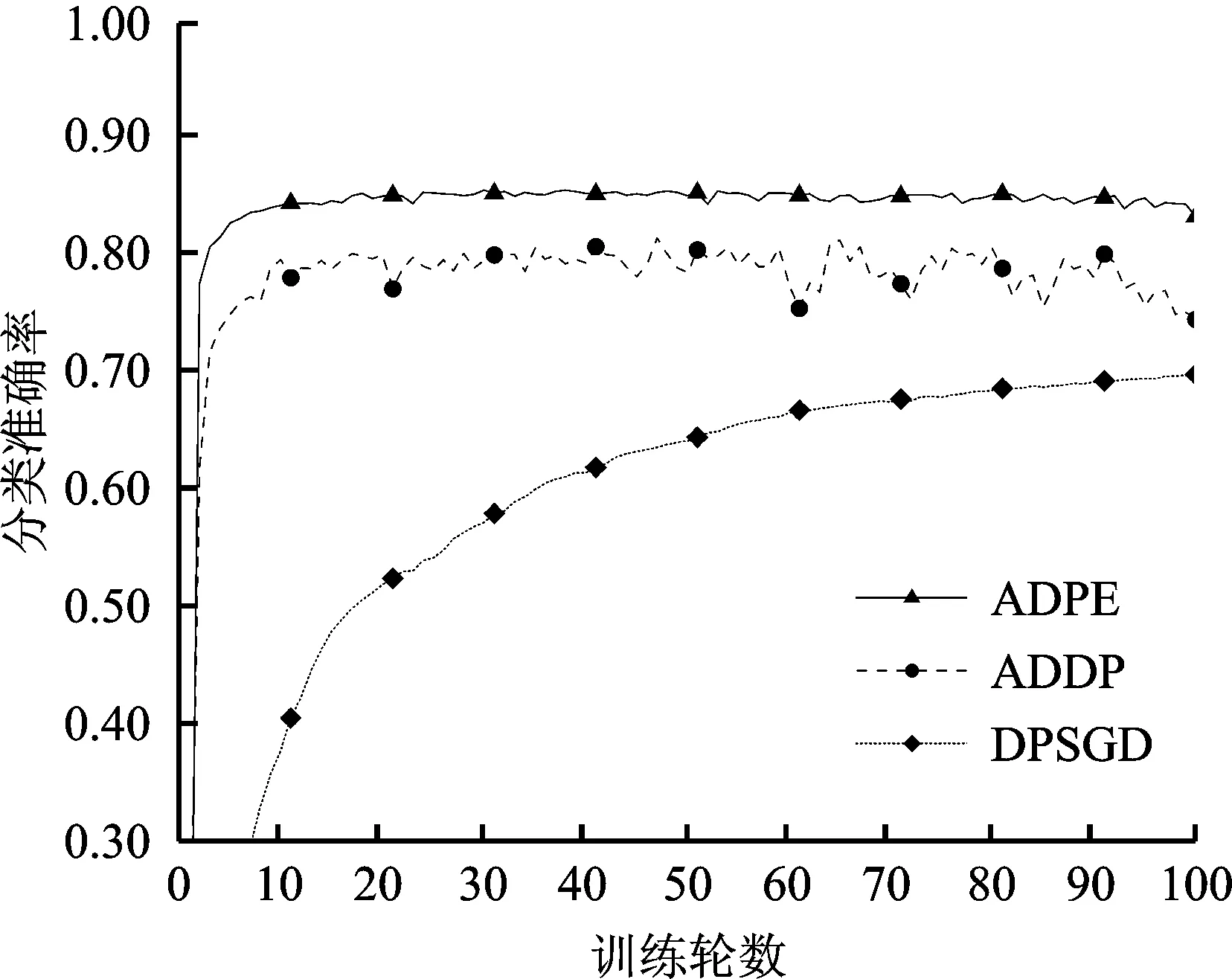
Pr[M(D)∈O] (1) 则称隐私机制M满足(ε,δ)-DP。其中,Pr[x]表示数据x泄露的概率;ε为隐私预算,用来衡量隐私保护的程度,ε越小,隐私保护程度越高;δ为违反隐私机制M的概率,δ=0时隐私机制M满足严格差分隐私,即ε-DP。 定义2全局敏感度[10]。给定数据集D上的一个查询函数f:D→Rd,f的全局敏感度是指删除数据集中任何一条记录所引起查询结果的最大变化,定义为 (2) 其中,D和D′是任意两个相邻数据集,l表示度量距离的向量范数,通常为1或2范数距离。 在训练深度神经网络模型时,由于迭代次数较多,对隐私损失的估计至关重要。零集中差分隐私[21](zero-Concentrated Differential Privacy,zCDP)是一种新的差分隐私松弛形式,与(ε,δ)-DP相比,对多次迭代计算的隐私损失提供了更清晰和更严格的分析。zCDP的定义如下。 定义3zCDP[21]。对于任意α>1,若隐私机制M对于任意两个仅相差一条记录的相邻数据集D和D′满足: (3) 则称该隐私机制满足ρ-zCDP。其中,Dα(M(D)‖M(D′))表示M(D)和M(D′)间的α-Renyi距离,L(O)表示输出结果为O时,算法在两个数据集之间产生的隐私损失,即 (4) 文中使用到zCDP的一些性质和定理如下。 性质2[21]假设两种机制满足ρ1-zCDP和ρ2-zCDP,那么它们的组合满足(ρ1+ρ2)-zCDP。 性质3[21]若机制M满足ρ-zCDP,那么对于任意δ>0,M满足(ρ+2(ρlog(1/δ))1/2,δ)-DP。 SHAP[22](SHAPley additive explanations) 是一种对黑箱模型进行解释的方法。SHAP基于 Shapley值被解释为一种加性特征归因方法,以此衡量出每个输入特征对最终预测结果的贡献程度。模型的预测结果被解释为二元变量的线性函数,具体表示为 (5) 其中,g表示解释模型,M表示输入特征集合,φ0表示平均模型的预测,φi为每个特征i的Shapley值,其计算公式为 (6) 其中,V表示{Mxi}的子集合,分式表示不同特征组合对应的概率,f(xV∪{i})与f(xV)分别表示不同特征组合下xi入模和不入模时的预测结果。 笔者基于差分隐私的思想,在模型训练过程中,首先利用SHAP模型衡量每个输入特征对模型预测结果的贡献度,再根据贡献比例对每条原始数据在特征维度上进行自适应扰动,解除迭代次数与隐私预算之间的依赖;其次,基于函数机制原理,对损失函数进行泰勒展开,获取近似多项式并对其系数进行扰动,确保每条样本的真实标签信息不会被泄露。在每次参数更新时,通过自适应矩估计算法来优化梯度和调整学习率,从而加快模型的收敛速度。此外,还引入了零集中差分隐私的组合机制,对整个训练过程中隐私损失进行了更严格更清晰的度量。最终,文中所提的ADPE方案在保护了整个深度学习模型隐私的同时,极大地保证了模型训练的准确性和实用性。具体系统设计如图1所示。 图1 系统设计图 文中以卷积神经网络做为基础网络结构,每个隐藏层神经元的转换过程可表示为h=a(xWT+b),其中x为输入向量,h为输出,b为偏置项,W为权重矩阵。xWT+b表示线性变换部分,a(·)为激活函数。给定一个模型参数为θ的损失函数L(θ),通过在Nepoch轮训练中应用Adam算法优化数据集D上的损失函数L(θ)来训练卷积神经网络。其中,每个训练轮次进行Niteration次迭代,每批次训练样本B是D中大小为|B|的随机集合。 ADPE方案主要考虑白盒攻击[23],即敌手拥有该深度学习模型的全部知识,包括模型结构和参数,可以访问发布的模型而不只是训练过程。此时主要存在以下两种隐私泄露的威胁:① 敌手依据模型参数获取敏感信息甚至原始数据;② 敌手试图通过目标模型推断出某条目标样本是否参与过训练。 ADPE方案的具体流程主要分为5个阶段。需要注意的是,总迭代次数为训练轮数和每轮迭代次数的乘积。具体方案如算法1所示。 (1) 自适应噪声尺度的分配。不同的输入特征对预测结果影响程度是不同的,较重要的特征往往对预测结果起到决定性作用,而不重要的特征无论如何扰动都不会对结果产生太大影响。因此,可以将每个特征的贡献度作为分配噪声尺度的依据。 首先,读取批量数据进行特征维度上的贡献度计算,记作Ctrj,j∈[1,k],表示第j个特征对预测标签的贡献度。对于每个输入特征Mj,计算每个样本中该输入特征的SHAP值,将所有样本中该特征SHAP值累加求平均值,得到该特征的贡献度。其次,计算每个输入特征对于预测结果的重要性,即贡献比例 (2) 原始样本的扰动。考虑到原始样本只作为神经网络的输入被使用,在样本被输入神经网络时,构造自适应差分隐私机制,对每条数据添加高斯噪声以实现扰动,无需在每次迭代中都对模型梯度或权重加噪。这能够让隐私损失不受迭代次数的影响,提高了模型的准确性和实用性。具体地,对样本集合B中的每个样本xi中第j个输入特征值添加的噪声如下: (7) 其中,Δs1表示原始数据的敏感度。假设两个相邻样本集合B和B′中只有最后一个样本xn和x′n不同,且xi(Mj)被归一化到[0,1],则敏感度Δs1的计算如下: (8) 通过式(7)可以看出,某输入特征对预测结果的贡献度越小,所分配的隐私预算就越少,添加的噪声尺度就越大。这是因为对于这些因子而言,添加太多噪声对预测结果的影响不大。该过程衡量了隐私与效用之间的关系,即在提供隐私保护的同时,尽可能保证数据的可用性。 (3) 损失函数的扰动。由现有损失函数的定义可知,原始样本的真实标签值{y1,…,yd}参与了损失函数的计算,因此,为保护原始样本中的标签,可以根据函数机制原理[24]处理损失函数。文中采用sigmoid作为激活函数,交叉熵作为损失函数。具体表示如下: (9) 其中,HxiWT为最后一个隐藏层的输出。通过泰勒展开将损失函数在0处展开到二阶,具体如下: (10) (11) 其中,Δs2表示近似多项式系数的敏感度。同理,假设两个相邻样本集合B和B′中只有最后一个样本xn和x′n不同,则有[18] (12) s1=γ1s1+(1-γ1)gt, (13) (14) 其中,γ1和γ2表示指数衰减率。为防止s1和s2趋向0,通过计算偏差进行修正: (15) 最后,用优化的梯度更新参数: (16) 式中,ξ是为了维持数值稳定性而添加的常数。Adam算法将历史梯度作为先验知识,利用历史梯度的指数衰减平均值更新当前梯度,加快了模型收敛速度;同时利用历史梯度平方的指数衰减平均值更新学习率,使得模型收敛过程更加稳定。 算法1ADPE。 输入:总迭代次数T,每轮迭代次数Niteration,批次训练样本B,输入特征集合M={M1,…,MK},超参数学习率η,损失函数L(θ),噪声尺度σ1和σ2,全局敏感度Δs1和Δs2 输出:目标模型参数θT和总体隐私损失ρtotal ① 初始化模型参数θ0和隐私损失统计量ρ ②//确定自适应噪声尺度 ③ forj→1 toKdo ④ 计算输入特征Mj对预测标签的贡献度Ctr ⑦ end for ⑧ fort←1 toTdo ⑨ 获取批次训练集B中的每个样本xi ⑩//扰动原始样本 由节3.1可知,文中主要存在两种隐私泄露的威胁,二者本质上都是由于敌手可以从模型本身获取到隐私数据。首先,针对威胁①,在训练之前直接对原始数据进行加噪处理,从而在训练过程中减弱中间参数与原始数据的关联性,让敌手无法反推出真正准确的数据信息。其次,针对威胁②,通过加入满足差分隐私定义的噪声,使得相邻的两条数据样本无法区分,敌手就无法判断目标样本是否真实存在于训练数据集。因此,通过证明算法1满足差分隐私来论证对上述两种威胁的抵抗。 定理3算法1满足Nepochρ0-zCDP,即(ρ1+2(ρ1log(1/δ))1/2,δ)-DP。 文中的隐私损失统计部分可以扩展为隐私损失的动态监测机制,即给定zCDP的总隐私预算ρtotal,每轮训练之前都先判断:剩余的隐私预算减去本轮所需的隐私预算后是否大于0,大于0继续执行训练,从而保证整个训练的运行都满足ρtotal-zCDP。图2展示了当σmax=σ1=σ2=5时,随着训练轮数的增加,分别采用zCDP、 MA和(ε,δ)-DP来统计隐私损失的变化情况,其中δ=10-2。 图2 隐私损失与训练轮数的关系 使用MNIST和Fashion MNIST两种数据集进行实验验证。其中,MNIST数据集包含10种类别的手写数字图片,有60 000个训练样本和10 000个测试样本,每个样本由28×28个像素点的灰度图像构成。Fashion MNIST数据集由10种类别的服装正面图片组成,分为60 000个训练图像和10 000个测试图像,每个样本由28×28个像素点的灰度图像构成。 实验部署在操作系统为Windows 11 64位、CPU为12th Gen Intel(R) Core(TM) i7-12700H @2.30 GHz、GPU为Nvidia GeForce GTX2050 4GB和内存16 GB的工作站,基于Python 3.8仿真实验。预训练时使用DeepSHAP衡量输入特征对输出的贡献度,采用Tensorflow1.5.0训练深度学习模型,网络结构为卷积神经网络,包含2个特征分别为32和64、卷积核大小为5×5、步长为1的卷积层,2个2×2的最大池化层,以及2个神经元个数均为30的全连接层。利用Adam算法进行模型训练时基本参数设置为ξ=10-8,γ1=0.9,γ2=0.999,并结合指数衰减法优化学习率,使得模型在后期训练中更加稳定,所选择的批次样本大小为600。 主要进行两个实验:一是验证ADPE方案的有效性;二是将所提ADPE方案与现有方案在模型准确性上进行对比。 4.2.1 有效性验证 通过对比模型引入自适应差分隐私机制前后的模型准确率,来验证ADPE方案有效性。引入差分隐私机制前以常规的方式训练文中基础网络结构模型,称作基线模型,引入后在δ=10-5的情况下分别设置σ1=σ2=4,8,10。在训练轮数Nepoch=100时的结果如图3所示。 (a) MNIST数据集 由图3可知:① 引入ADPE方案的隐私保护机制对模型进行扰动时,模型的准确率不会明显降低。② 在MNIST数据集上,第10轮训练时,3种噪声条件下的模型准确率都达到约98%以上,第50轮训练后则趋于稳定,尤其是当σ=4时,中后期的训练效果与基线几乎一致,说明了模型较好的可用性。③ 由于Fashion-MNIST数据集的图像比MNIST数据集更复杂,因此模型的准确率没有MNIST数据集那么高,且模型中后期训练,包括基线模型在内,均不稳定,会有约1%的波动幅度,但总体的训练效果依然在约87%以上,说明了该方案的有效性。④ 对于不同的噪声尺度,噪声尺度越小,模型的分类准确率就越高,说明用户可以根据个性化需求调整噪声尺度,实现方案隐私和效用之间的平衡。 4.2.2 对比分析 研究所提方案ADPE与经典方案DPSGD[13]和较为先进的方案ADDP[19]对模型提供隐私保护时的对比情况。针对3种方案,设置Nepoch=100,δ=10-4,当取不同隐私预算时,3种方案在2种数据集上的分类准确率随训练轮数的变化情况如图4和图5所示。 其中,ADPE方案采用节3的公式得出隐私预算和噪声参数的关系。 (a) ε=0.5 (a) ε=0.5 由图4和图5可知:① 随着隐私预算的增大,所添加的噪声逐渐减少,3个方案的模型分类准确率都呈上升趋势。② 隐私预算相同的情况下,所提ADPE方案在2种数据集上的模型分类准确率都高于对比方案,说明ADPE方案的性能较优。具体表现为,在较大的隐私预算ε=4时,方案的模型在MNIST数据集上能达到约98.7%的准确率,在Fashion-MNIST数据集上准确率后期最高约为89.7%。③ 在MNIST数据集上,当隐私预算ε=0.5时,ADDP方案难以达到收敛状态,波动剧烈,而ADPE和DPSGD方案表现较为平和,这说明加入高斯噪声更有利于模型的稳定。随着隐私预算的增大,ADPE和ADDP方案在20轮训练后都趋于稳定,甚至ADPE方案在10轮左右就基本收敛,而DPSGD方案在训练100轮后还未达到明显的收敛状态。④ 在Fashion-MNIST数据集上,由于其样本结构的复杂性,ADPE方案和ADDP方案出现一定程度的波动,但前者的波动范围较小,后者的波动范围较大,而DPSGD方案仍然收敛较慢。综上可见,ADPE方案在加快模型收敛的同时具有一定的稳定性。 笔者提出了一种基于自适应差分隐私的高效深度学习方案,有效平衡了模型的隐私性和可用性。该方案基于沙普利加性解释模型设计了一种自适应差分隐私机制,用于保护原始数据样本,并利用函数机制扰动原始标签,增强了深度模型训练的隐私性。同时,引入零集中差分隐私的组合机制度量整个训练过程的隐私损失,使得方案有更好的隐私保证。通过在两个经典数据集MNIST和FashionMNIST上的实验分析表明,所提方案能够在保护隐私的前提下尽可能实现较高的模型准确率,并且加快了模型收敛速度以及保证了模型中后期训练的稳定。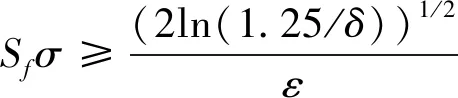
2.2 零集中差分隐私

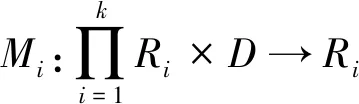
2.3 SHAP
3 方案设计
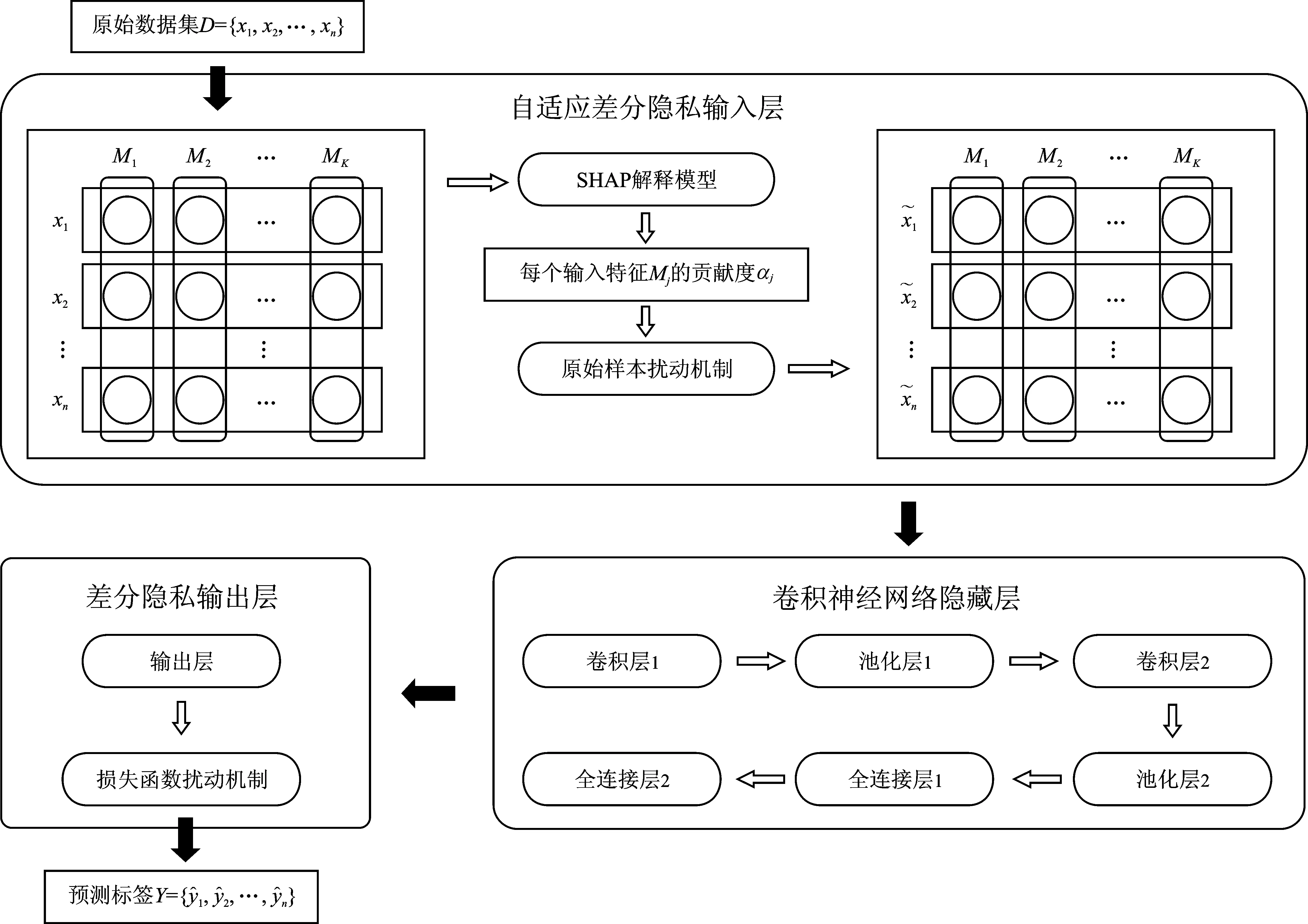
3.1 模型框架
3.2 具体流程

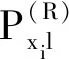
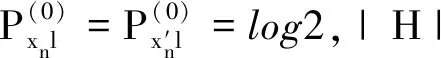
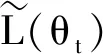
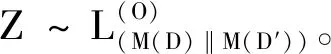
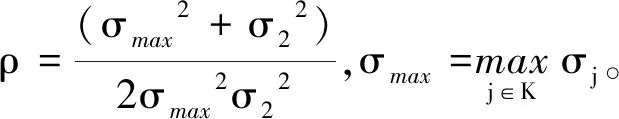
3.3 隐私性分析
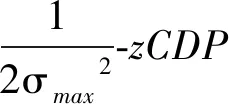
4 实验与分析
4.1 实验设置
4.2 实验结果
5 结束语

