面向航班延误场景的机位预分配模型及算法研究

王鑫晨, 吕增威,2, 魏振春,2, 张 浩

(1.合肥工业大学 计算机与信息学院,安徽 合肥 230601; 2.安全关键工业测控技术教育部工程研究中心,安徽 合肥 230601; 3.飞友科技有限公司,安徽 合肥 230031)

0 引 言

近年来,随着中国民航业的迅猛发展,旅客需求及机场数量不断增加,飞机已成为主要的运输选择之一。机位是机场的关键资源,是乘客上下飞机和维护飞机的重要场所,高效地利用停机位资源可以提高机场的容量和服务效率。如何在机位资源有限条件下为到港的每架航班分配合适的停机位,以提升乘客满意度和实现机场的服务效率,被称为机位分配[1]。机位分配问题多年来一直是一个热门的研究课题[2-3],是航空公司运营和管理的核心环节。

在机位分配研究中,现有文献大部分研究普适性更高场景下的机位分配问题,以保证机场的正常运行,少部分学者研究了航班延误场景下的机位分配问题。针对航班延误场景下航班时刻表易出现扰动问题,文献[4]提出了新的二元整数规划模型来解决机位再分配问题,该模型将乘客换乘的成功率作为目标函数进行评估。为解决机场航班延误问题,文献[5]提出了一种具有较高鲁棒性的机位分配模型,以最小化机位空间时间为目标,并利用双流国际机场的数据进行仿真验证,结果表明所提模型稳定性优于现有模型。然而在航班延误场景下,现有研究大多以最小化机位空间时间为目标来解决机位冲突问题,较少考虑航班冲突概率与机位空闲时间的密切关系。最小化航班冲突概率可以更有效地避免因航班延误造成的预分配机位变更问题,使得机位分配方案具有更高的鲁棒性和抗延误性,也可大幅降低机位再分配的难度。

针对机位分配问题,现有文献大部分采取精确算法、启发式算法等算法来求解,较少采用深度强化学习方法。文献[6]将停机位分配问题建模为马尔可夫决策模型,提出了基于策略梯度的机位分配算法来求解该问题。由于深度强化学习技术的迅猛发展,已经有大量学者采用深度强化学习方法来解决机场领域的优化问题。针对大型机场航班的离港管理问题,文献[7]将该问题建模为马尔可夫决策过程,提出了一个强化学习模型来解决该问题,并选取世界上最繁忙的机场之一肯尼迪国际机场进行仿真验证。文献[8]以机场货运资源优化为目标,将深度强化学习技术应用于机场货运业务的仿真模型开发,提出了将深度强化学习与机场货运业务仿真模型相结合的决策支持系统框架。

针对现有研究的不足,本文首先建立了航班延误场景下的停机位分配模型,并将其建模为马尔可夫决策模型,提出基于深度强化学习的机位分配算法进行求解,以解决航班延误场景下的预分配机位变更问题。

1 系统模型

1.1 模型参数定义

设进离港航班集合为U={1,2,…,N},N为航班数量;停机位集合为G={1,2,…,M},M为停机位数量。航班信息包括计划到港时刻、计划离港时刻、航班型号、上下机旅客人数;停机位信息包括停机位的数量及其属性等。采用变量xik表示航班i与停机位k的分配关系,当航班i被分配至停机位k中,则xik=1;否则xik=0。ui、vi分别代表航班i计划到港时刻和计划离港时刻,mi表示航班i的机型,gk表示停机位k的大小属性。设li为航班i的属性,若航班i为国际航班,则li=1;若航班i为国内航班,则li=0。同理,ok为机位k的属性,若ok=1,则机位k仅供国际航班停靠;否则ok=0。

1.2 预分配约束条件

为保证航班安全到港,需要充分考虑机位分配过程中的安全要求规则、运行规则等信息,本文考虑为航班分配机位所需满足的约束条件如下:

xik+xjk≤1, ∀Rij=1,∀i,j=1,…,N, ∀k=1,…,M

(1)

Tjk=(uj-vi)yijk

(2)

(3)

lixik=ok, ∀i=1,…,N,∀k=1,…,M

(4)

∀k=1,…,M

(5)

(gk-mi)xik≥0, ∀i=1,…,N,∀k=1,…,M

(6)

|Cik-Djl|≥βxikxjlzkl

(7)

|Djl-Dik|≥βxikxjlzkl

(8)

|Cjl-Cik|≥βxikxjlzkl

(9)

式(1)为鲁棒性约束。定义同机位两架连续航班之间的冲突概率大于q,则这两架航班不可分配到同一机位,该约束能有效避免可能发生的机位占用冲突。对于分配至同一机位上的两架航班i和j,pij表示航班i与航班j可能面临的机位冲突概率[9],并引入Rij表示航班i与航班j的机位冲突概率pij与q的大小关系,若pij≥q则Rij=1;否则Rij=0。

式(2)为同机位空闲时间定义,其中Tjk表示机位k中航班j与紧前航班i的空闲时间,若航班i与航班j停靠同一机位k,且航班i是航班j的前驱航班,则yijk=1;否则yijk=0。

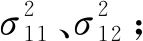
式(4)为停机位区域约束。

式(5)是唯一性约束,即航班进港时必须为其分配停机位,且仅可分配至一个停机位。

式(6)为机型匹配约束。

式(7)为出入冲突约束,其中β为避免冲突所需的安全时间间隔,若机位k与机位l为相邻机位,则zkl=1;否则zkl=0。Cik表示航班i进入机位k的时刻,即Cik=uixik;Djl表示航班j离开机位l的时刻,即Djl=vjxjl。

式(8)和式(9)分别为双入和双出冲突约束。

1.3 预分配目标函数

恶劣天气、航班延误和航班取消等干扰在机场运营中屡见不鲜,可能会出现机位占用冲突使得复杂的机位预分配计划被打乱,并可能导致严重的后果。现有研究主要通过设置同机位最小安全时间间隔约束以避免机位冲突,然而同机位连续航班间的空闲时间并不能较准确地反映两架航班之间的机位冲突。故本文根据机位冲突概率理论增加了机位冲突概率最小化优化目标,该机位预分配模型不但可以大幅提升旅客的满意度,而且具有较好的抗延误特性。

1.3.1 最小化机位冲突概率

由于恶劣天气时常出现,航班延误现象经常发生,建立具有较高鲁棒性的机位分配方案非常重要。机位冲突概率可以更准确地表达同机位两航班在延误场景下可能存在的冲突概率大小,进而可以通过调整机位冲突概率以避免冲突。因此,本文以最小化机位冲突概率为第1个优化目标,即

(10)

1.3.2 最大化乘客靠桥率

乘客满意度对于机位分配的结果尤为重要。航班降落到达机场时,离港和到港乘客会更偏向于较短的步行距离以及等待时间。由于航班被分配至近机位时,乘客的步行距离更短,乘客的满意度会更高。相反,若航班被分配至远机位,乘客须乘坐摆渡车到达停机位或返回行李寄存处,乘客满意度较低。本文以最大化乘客靠桥率作为第2个优化目标,即

(11)

其中:Gn为近机位的集合;bi、hi分别为从航班i进港和从航班i离港的旅客人数。

1.3.3 组合优化目标

根据上述对优化目标以及约束条件的阐述,本文综合考虑了机场及旅客利益,以最大化乘客靠桥率和最小化机位冲突概率为组合优化目标。组合优化目标表示如下:

s.t.式(1)～式(9)

其中,W为权重系数,根据每个目标的重要性,对不同数据组合的多个实验进行分析,最终确定更合适的权重系数值。

2 基于强化学习的机位和分配算法

本文提出的优化问题属于NP-hard问题[10],由于约束条件较多,局部最优解之间高度离散。以往的研究大多采取传统算法进行求解,然而传统算法从一个局部最优解探索到另一个局部最优解非常困难,因此容易陷入局部最优。深度强化学习算法极其适合于解决复杂顺序决策问题[11],然而由于基于行动者-评估家(actor-critic,AC)框架的深度强化学习算法收敛较慢,本文引入异中的概念,即异步优势动作评价(asynchronous advantage actor-critic,A3C)算法。A3C算法是基于AC框架的异步训练方法,由于多智能体并行与环境交互学习动作策略,因此收敛速度较快。

2.1 马尔可夫决策过程建模

强化学习算法中有3个关键因素需要确定,分别为状态空间、动作空间和立即奖励的定义。

1) 状态空间。定义在时间步t的状态空间St=〈B(t),Gpro,E(t),H(t)〉。其中:B(t)表示当前时间步t各停机位仍需被占用的时间;Gpro表示各停机位的属性,分别包含远近属性、大小属性和国际国内属性;E(t)表示在时间步t的进离港时刻信息;H(t)表示时间步t的航班属性信息,分别包含第t架航班的登机人数、下机人数、大小属性和国际国内属性。

2) 动作空间。动作空间A描述的是在时间步t时智能体可采取的动作at(at∈A)的集合。其中,at∈{1,2,…,M}表示航班t必须从集合{1,2,…,M}中选取一个动作,即必须停靠且仅可停靠一个停机位。智能体可采取的动作at需根据约束条件进行缩减。

3) 立即奖励。智能体每执行一个动作,就会获得一个立即奖励r。立即奖励应与优化目标有关,故预分配模型在时间步t的立即奖励rt表示为:

(1-W)yitkpit

(12)

2.2 基于异步优势动作评价的机位预分配算法

为求解本文问题,本文在非并行A2C(adrantage actor-critic)算法基础上提出了一种基于异步优势动作评价的机位预分配算法(gate assignment algorithm based on asynchronous advantage actor-critic,GABA3C)。非并行A2C算法基于AC框架,仅含有1个Actor网络和1个Critic网络,智能体与环境互动以学习最优的策略。而本文所提GABA3C算法设置了1个全局网络和多个AC结构,每个智能体即AC结构并行与环境进行互动学习动作策略,并将学习到的梯度反馈给全局网络,由全局网络更新自身参数,因此学习效率更高、收敛速度更快,这是本文所提算法的改进之处和创新点。A3C算法引入了优势函数A(s,a)[12],表明智能体在当前状态下采取行动a后所具有的优势值。优势函数定义如下:

A(s,a)=rt+γrt+1+…+γn-1rt+n-1+γnV(s′)-V(s)

(13)

其中,V(s)和V(s′)的值是通过Critic网络学习所得到的。各个线程中的Actor网络损失函数定义如下:

(14)

在A3C结构中,Actor和Critic网络采用n步TD(temporal difference)误差法[13]学习动作概率函数和值函数。在本算法的学习方法中,n步TD误差的计算是通过初始状态的状态估计值V(s0)与n步后的估计值的差来实现的,即

e=r0+γr1+γ2r2+…+γn-1rn-1+γnV(sn)-V(s0)

(15)

其中,γ为折扣因子。TD误差反映了Actor网络中所选行为的好坏,Critic网络损失函数定义如下:

(16)

在计算TD误差后,A3C结构中的每个Worker网络不直接更新其网络权值,而是用其计算出的梯度更新Global网络的参数。更新公式如下:

θ=θ+αa(dθ+θ′lgπ(a|s;θ′)A(s,a))

(17)

(18)

其中:θ为Global网络中Actor网络的权值;θ′为Worker网络中Actor网络的权值;θv为Global网络中Critic网络的权值;θv′为各个Worker网络中Critic网络的权值;αa和αc分别为Actor和Critic网络的学习率。

GABA3C算法伪代码如下:

输入:航班信息表及机位占用信息

输出:机位分配结果

初始化t←1,ep←1;

while ep<=EP-MAX do

初始化Global网络中Actor参数为θ,Critic参数为θv。初始化AC结构中Actor参数θ′←θ,Critic参数θv′←θv;

tstart=t;

初始化梯度dθ←0和dθv←0;

初始化环境状态st;

whilest不是终止状态 andt-tstart≠tmaxdo

根据Worker网络中的策略π(at|st;θ′)选择动作at,即第t架航班选择at号机位停靠;

获得立即奖励rt和新状态st+1,执行t←t+1;

end

ifst为终止状态

R←0;

else ifst为非终止状态

R←V(st,θv′);

fori∈{N-1,…,1}

R←ri+γR;

计算Actor梯度:dθ←dθ+θlgπ(ai|si;θ′)A(si,ai);

end for

梯度dθ和dθv计算完成后,通过式(17)、(18)更新Global网络中的θ和θv;

ep←ep+1;

end

策略网络πθ拟合后,将初始状态s0输入到πθ中,进行N次迭代,得到预分配的机位分配结果。

3 仿真分析

3.1 参数设置

本节介绍基于异步优势动作评价的机位预分配算法参数设置。本实验设置场景实例SCE-1,具体参数如下:航班数量N=42,机位数量M=17,最小安全时间间隔β=3 min,冲突概率p=0.16。设置最大迭代次数EP-MAX=10 000,Worker网络数量为3。Actor和Critic都设置为全连接神经网络,学习率分别为0.001和0.002。设置折扣因子γ为0.9。航班起飞延误中,两正态分布的均值和方差分别为μ11=0.255,σ11=6.403以及μ12=15.330,σ12=14.962;航班到达延误分布的均值μ2=0.175,方差σ2=7.849。

3.2 预分配仿真结果及对比分析

在仿真实验中,利用我国某中型机场的实际运行数据进行模型仿真与算法实现。为了验证所提GABA3C算法的性能,本文进行了一系列仿真,来评估本文的GABA3C算法性能,并与自适应并行遗传算法(adaptive parallel genetic algorithm,APGA)[14]、近端策略优化(proximal policy optmization,PPO)算法以及深度Q网络(deep Q-network,DQN)算法进行对比。针对不同权重系数,在场景实例SCE-1下采用4种算法运行20次获得目标数据,见表1所列。本文以W=0.4作为机位预分配模型的权重系数。

本文在训练过程中记录每代的总奖励值,即目标函数值,为GABA3C算法训练的目标函数值随迭代次数变化关系,如图1所示,由图1可知GABA3C算法训练效果显著。

图1 GABA3C算法的收敛性能

由于机位预分配的目标优化模型是一个NP-hard问题,采用GABA3C算法来寻找最优解,得到的停机位分配结果用甘特图表示,如图2所示。图2中:0～10号机位为近机位;11～16号机位为远机位,10、15、16号机位仅供国际航班使用;其余机位供国内航班使用,每架航班都标注了航班号。

图2 机位分配甘特图

根据表1和图2可以发现,GABA3C算法求得的解在乘客靠桥率方面已达到63.78%,乘客的满意度得以提升。另外,机位冲突总概率也较小,仅仅为1.025,可以有效避免因航班延误造成的机位预分配结果变更问题。

由表1可知,当权重系数为0.4时,在机位冲突概率方面,GABA3C算法获得的解分别比APGA、PPO、DQN算法低23.5%、10.0%、17.4%,故所提算法能够有效避免因航班延误造成的机位变更问题;同时,在近机位乘客分配率方面,GABA3C算法获得的解分别比APGA、PPO、DQN算法高5.7%、4.6%、5.8%,故本文算法能够较好地提高旅客的满意度。为了验证本文所提算法在各种变化场景下的适用性,本节新增2组不同机场实际运行数据的场景实例(SCE-2、SCE-3)对本文算法进行分析,其中SCE-2场景实例中具体参数设置如下:航班数量N=30,机位数量M=15,冲突概率p=0.16,最小安全时间间隔β=4 min;SCE-3场景实例中具体参数设置如下:航班数量N=38,机位数量M=14,冲突概率p=0.16,最小安全时间间隔β=3 min。

为保证公平性,3组场景实例冲突概率p都设置相同,最小安全时间间隔由不同机场规则要求确定。

针对3组不同场景实例,分别采用4种算法运行20次绘制盒状图,如图3所示。

图3 不同场景实例下4种算法的目标函数值比较

由图3可知,3组不同场景实例下,GABA3C算法获得的解的最大值、最小值、中位数均比其他3种算法更高,故本文所提算法在不同场景下的适用性较好,所获得解的质量更高,具有很强的寻优性能和较强的稳定性。

为了测试算法改进前后的性能增益,本文针对3组不同场景实例分别设置消融实验,分别采用非并行A2C算法和GABA3C算法运行20次,获得最优目标数据见表2所列。

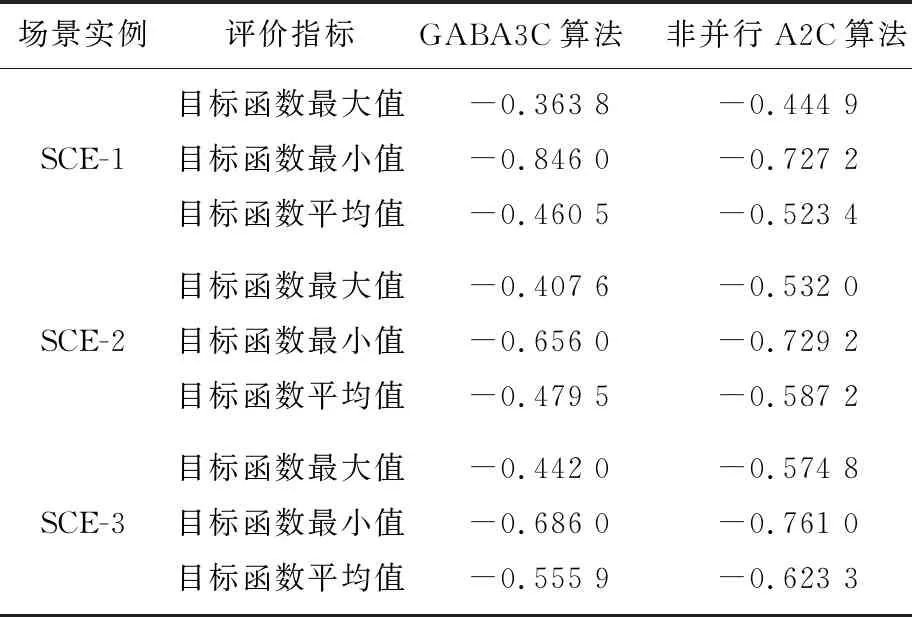
表2 不同场景实例下的消融实验结果

由表2可知,在不同场景实例下,相比于非并行A2C算法,GABA3C算法获得的解在3个评价指标上的值更优。因此,本文所提算法能够更好地避免因航班延误造成的机位冲突问题的同时,还能够显著提升旅客的满意度。

4 结 论

针对航班延误场景下因航班延误带来的预分配机位变更问题,本文提出了具有良好抗延误特性的机位预分配模型,并将其建模为马尔可夫决策模型,提出了基于异步优势动作评价的机位预分配算法来求解该问题。为验证所提算法在各种变化场景下的适用性,本文设置了3组场景实例。仿真实验表明,本文所提GABA3C算法在提升旅客满意度的同时,还可以有效避免因航班延误造成的机位冲突问题。