顾及电离层延迟的BDS-3四频长基线定位算法

吕 震,王振杰,刘金萍,翟建朋,周 浩

(1. 中国石油大学(华东) 海洋与空间信息学院,山东 青岛 266580; 2. 中石化石油工程地球物理有限公司胜利分公司,山东 东营 257100; 3. 青岛北斗陆海科技有限公司,山东 青岛 266555)

在长距离相对定位中,电离层延迟作为信号传播过程中的主要的误差源之一,很大程度上会影响定位精度。国内外学者针对电离层延迟问题展开了大量研究。对于单频用户而言,常采用电离层模型对电离层进行修正,常用的模型包括美国GPS广播电离层Klobuchar模型[1],国际参考电离层IRI(international reference ionosphere)模型[2]、欧洲Galileo系统广播电离层NeQuick模型[3],以及我国北斗三号全球导航卫星系统自主设计研制的北斗全球广播电离层延迟修正模型(beidouglobal broadcast ionospheric delay correctionmodel,BDGIM)[4]等。在利用双频信号进行高精度定位解算时,依据电离层延迟与信号频率的平方成反比的关系,通过利用双频消电离层组合模型消除观测值中电离层延迟[5]。此外,也可依据双频数据对总电子含量(totalelectroncontent, TEC)进行提取[6],通过建立全球电离层模型(globalionospheremap, GIM)反映电离层TEC的时空分布和电离层活动规律[7]。随着卫星信号频率的增加,一些学者在双频信号的基础上采用三频信号对定位中电离层延迟问题展开进一步研究,文献[8]基于实测的北斗三频数据,同时对双频消电离层组合和三频最小噪声消电离层组合的伪距差分定位性能进行对比分析。文献[9]在GPS载波和码观测量的双频电离层改正方法基础上融合电离层折射误差三频二阶改正方法,并采用GPS三频观测数据对该方法进行了验证。文献[10]针对不同频率组合噪声放大程度不相同的问题,对双频消电离层一阶项观测组合和三频消电离层一阶及二阶项观测组合表达式进行推导,并对观测组合定位精度进行分析。文献[11]基于三频相位观测值提出了一种适用于长距离双差电离层延迟量实时估计的方法。此外,利用三频观测数据对TEC及其变化率进行计算也可达到描述电离层形态和结构的目的,进而实现高精度定位[12-13]。

上述文献主要采用3个频率以内的信号对定位中电离层延迟问题展开研究,而我国北斗三号全球卫星导航系统(BeiDou Navigation Satellite System, BDS-3)具有提供四频信号的优势,在长基线场景下利用四频信号对相对定位性能进行研究具有一定意义。为此,本文针对BDS-3四个频点的信号:B1C(1 575.420 MHz)、B1I(1 561.098 MHz)、B2a(1 176.450 MHz)、B3I(1 268.520 MHz)组成四频组合观测值,首先对基于GB-FCAR(geometry-based four-frequency carrier ambiguity resolution)模型的电离层延迟参数估计方法进行介绍;然后提出一种四频消电离层(ionosphere-free, IF)组合定位解算方法,该方法通过构造消电离层组合观测值达到消除电离层延迟的目的,并联合模糊度改正后的超宽巷或宽巷组合观测值从而实现原始窄巷模糊度和三维基线坐标的解算。试验选择两条超过500 km的长基线,将提出的四频IF组合方法和电离层延迟参数估计方法的定位精度对比分析。

1 四频组合系数优选准则

利用BDS-3四个频率的伪距或相位观测值可以组成具有不同波长、不同电离层延迟影响及不同观测噪声的组合观测值。特性良好的组合观测值需要满足波长较长、电离层延迟影响较弱、观测噪声较小的特点,但有时会出现电离层延迟尺度因子或噪声放大因子的绝对值达到最小时组合波长仍相对较小的情况,为此,本文考虑了除电离层延迟和观测噪声之外的对流层延迟误差和卫星轨道误差,在假设观测值中各误差项精度已知的情况下,通过定义总噪声水平(total noise level, TNL)确定最优组合系数[14-15]。伪距和载波相位的总噪声分别为

(1)

(2)

显然,在对伪距和相位线性组合进行优选时应分别以σTP=min和σTφ=min作为优选条件。表1列出了长基线情况下(基线长度大于500 km)双差伪距和相位观测值各误差项的精度。

表1 长基线观测值各项误差精度 m

2 基于GB-FCAR模型的电离层延迟参数估计方法

GB-FCAR模型是一种基于有几何模式的四频逐级固定模糊度模型,相较于无几何模式下的FCAR模型,该模型的优势为不仅可以对模糊度参数进行解算,还可以对位置参数等其他参数进行估计。在长基线定位中,电离层延迟残差会对模糊度解算效率和定位性能产生影响,若不做处理,在进行平差计算时电离层延迟残差会被模糊度参数和位置参数吸收,使最终的模糊度固定成功率和定位精度下降。为此,在GB-FCAR模型的待估参数中加入电离层延迟参数,并以一阶电离层延迟尺度因子作为其系数,采用最小二乘平差方法同时对电离层延迟参数、位置参数和模糊度参数进行求解。

对于GB-FCAR模型而言,需要1组四频伪距组合系数和4组四频相位组合系数。假设四频伪距组合系数为(m,n,p,q);4组四频相位组合系数为(is,js,ks,ls)s=1,2,3,4。因此GB-FCAR模型及展开式分别为

(3)

(4)

(5)

(6)

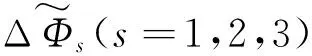
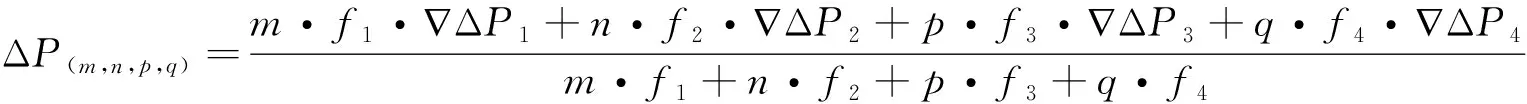
(7)

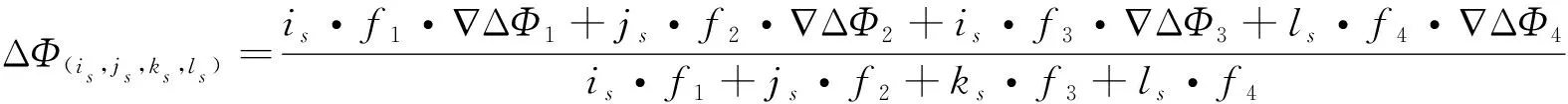
(8)

式中,∇ΔP1、∇ΔP2、∇ΔP3和∇ΔP4分别代表信号的4个不同频点上的伪距观测值;∇ΔΦ1、∇ΔΦ2、∇ΔΦ3和∇ΔΦ4分别代表信号的4个不同频点上的相位观测值。

根据GB-FCAR模型,伪距组合系数用于在第一步中与第1组超宽巷组合观测值共同求解第1组超宽巷模糊度,因此伪距组合系数仅选择1组即可。依据σTP=min原则对伪距组合系数进行优选。本文将搜索范围设置在[-5,5],通过筛选,搜索范围内BDS-3的四频最优伪距组合为(5, 5, 2, 3);然后还需要选择3组高质量的超宽巷或宽巷相位组合系数(i1,j1,k1,l1)、(i2,j2,k2,l2)、(i3,j3,k3,l3),依据σTφ=min原则对相位组合进行优选,将搜索范围设置在[-10,10];最终优选后的3组BDS-3四频超宽巷或宽巷组合系数分别为(1, -1, 0 ,0)、(0, 1, 2, -3)、(-1, 2, 2, -3)。第四组相位组合系数选用原始窄巷组合系数为(1, 0, 0, 0)。

3 四频消电离层组合方法

为了构造适用于四频信号的消电离层组合观测值,首先对4个原始相位观测值进行线性组合[16],公式为

∇ΔΦ(a,b,c,d)=a∇ΔΦ1+b∇ΔΦ2+c∇ΔΦ3+d∇ΔΦ4

=(a+b+c+d)(∇Δρ+∇ΔT)-β(a,b,c,d)∇ΔI1-

λ(a,b,c,d)∇ΔN(a,b,c,d)+∇Δε(a,b,c,d)

(9)

式中,(a,b,c,d)为相位组合系数;β(a,b,c,d)为一阶电离层延迟尺度因子;λ(a,b,c,d)为组合波长;∇ΔN(a,b,c,d)为组合模糊度;∇Δε(a,b,c,d)为组合相位观测噪声。

其中,一阶电离层延迟尺度因子、组合模糊度、组合相位观测噪声的表达式分别为

(10)

∇ΔN(a,b,c,d)λ(a,b,c,d)=(aλ1∇ΔN1+bλ2∇ΔN2+

cλ3∇ΔN3+dλ4∇ΔN4)

(11)

∇Δε(a,b,c,d)=a∇Δε1+b∇Δε2+c∇Δε3+d∇Δε4

(12)

(13)

其中,观测噪声放大因子为

(14)

为了满足几何相关、消除电离层延迟的影响、观测噪声达到最小的要求,相位组合系数(a,b,c,d)需要满足[17]

(15)

虽然消电离层组合可以消除电离层延迟的影响,但由于其虚拟波长太小,难以解决实际观测中的模糊度问题。因此将四频消电离层组合模糊度分解[18],公式为

∇ΔNIFλIF=cΦ1∇ΔNΦ1+cΦ2∇ΔNΦ2+

cΦ3∇ΔNΦ3+cΦ4∇ΔNΦ4

(16)

式中,∇ΔNΦ1、∇ΔNΦ2、∇ΔNΦ3为分解后的3个超宽巷或宽巷模糊度;∇ΔNΦ4为分解后的原始窄巷模糊度;cΦ1、cΦ2、cΦ3、cΦ4为对应4个组合模糊度的系数。

根据式(11)对式(16)进行进一步推导为

(17)

式中,T为线性组合系数矩阵;WIF为原始相位模糊度的系数矩阵。

若得到CIF,必须保证T可逆,即4个线性组合相互独立。将(i1,j1,k1,l1)、(i2,j2,k2,l2)、(i3,j3,k3,l3)表示为3个互不相关且满足系数和为0的超宽巷或宽巷组合系数,(i4,j4,k4,l4)表示1个满足系数和为1的原始窄巷组合系数。则CIF公式为

(18)

相位组合系数优选同样遵循σTφ=min原则,优选出3组合适的BDS-3超宽巷或宽巷组合系数分别为(1,-1,0,0)、(1,0,3,-4)和(-1,2,2,-3),原始窄巷组合系数同样选择(1,0,0,0)。BDS-3消电离层组合各项参数见表2。

表2 BDS-3消电离层组合各项参数

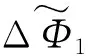
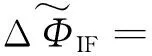
(19)

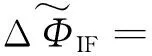
(20)

4 算例分析

本文数据为IGS提供的2021年年积日第200天SUTM(32.38°S,20.81°E)、WIND(22.57°S,17.09°E)、MET3(60.22°N,24.39°E)、SOD3(67.42°N,26.38°E)4个测站的BDS-3四频观测数据,观测时间为24 h,采样间隔为30 s,卫星截止高度角设为10°。试验选择2条基线,其中由SUTM和WIND测站组成的基线称作基线1,长度为620.45 km,由MET3和SOD3测站组成的基线称作基线2,长度为726.59 km。

首先对卫星可用性进行分析。基线1和基线2在观测时段内所观测到的卫星数与PDOP值分别如图1和图2所示。可以看出,两条基线BDS-3卫星的可视卫星数均超过4颗,卫星可见数均满足定位需求。2条基线的PDOP值均小于4,说明2条基线在观测时段内卫星分布均是良好的。

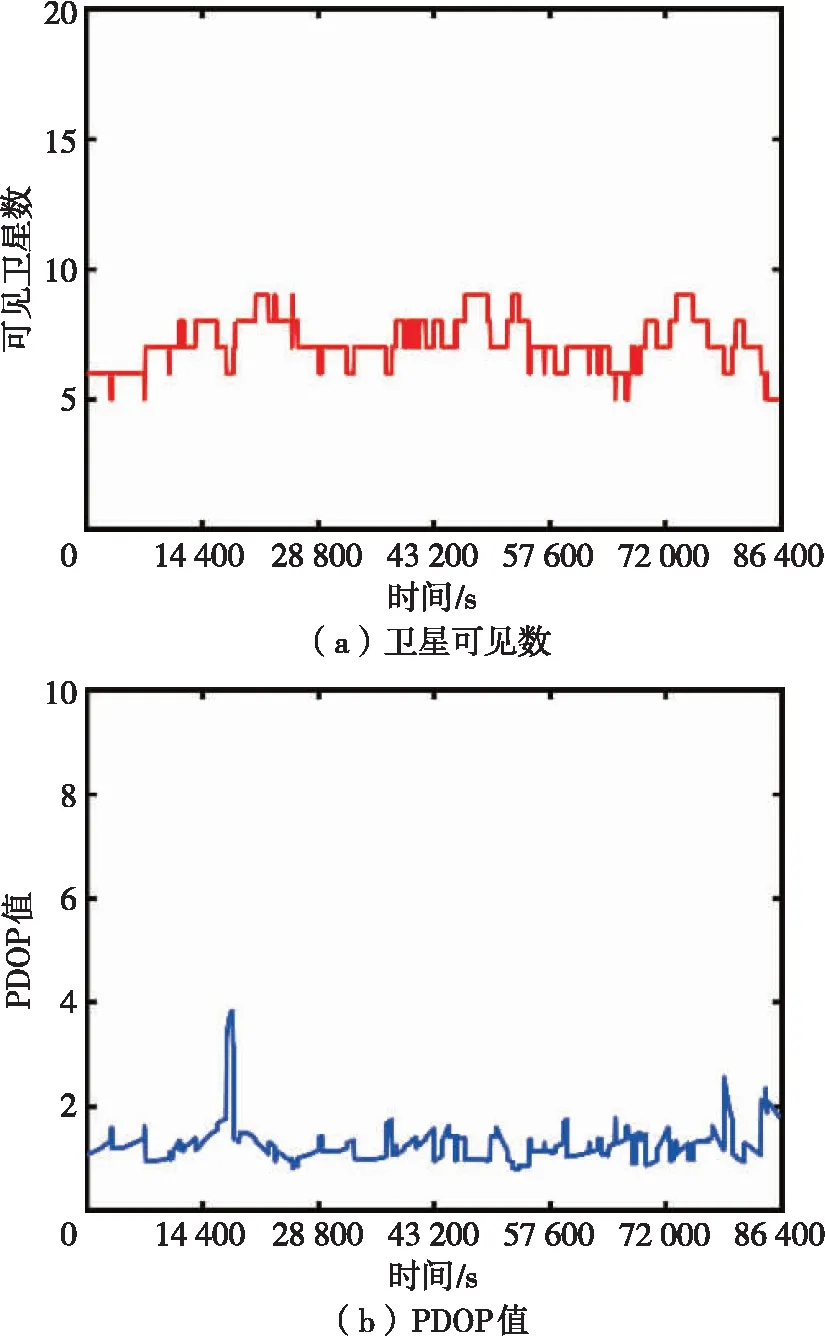
图1 基线1卫星可见数与PDOP值

四频IF组合方法与GB-FCAR模型均可实现对原始窄巷模糊度的解算,因此,依据模糊度固定成功率指标,对两种模型的原始窄巷模糊度固定性能进行初步评估。表3和表4分别列出了2条基线BDS-3部分卫星对的原始窄巷模糊度固定成功率。可以看出,在原始窄巷模糊度固定性能方面,四频IF组合方法可达到与GB-FCAR模型基本一致的水平。由于本文针对的是超过500 km的长基线,两测站所处空间环境相关性较弱,无法保证各项误差完全消除,因此导致了原始窄巷模糊度固定成功率较低。

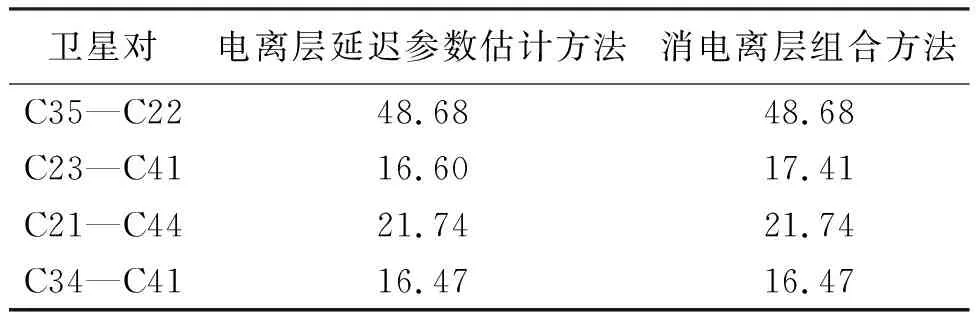
表3 BDS-3基线1原始窄巷模糊度固定成功率 (%)

表4 BDS-3基线2原始窄巷模糊度固定成功率 (%)

最后对两种不同的电离层延迟处理方法所解算的北、东、天方向的定位结果偏差进行分析。图3和图4分别对应两条基线下BDS-3定位结果偏差。可以看出,采用电离层延迟参数估计方法进行定位时,某些时刻明显会出现较大的定位偏差,存在水平和垂直方向上偏差绝对值超过2 m的情况,而四频IF组合方法的水平和垂直方向定位偏差明显更加稳定,稳定性明显提升,波动范围保持在[-2,2] m。

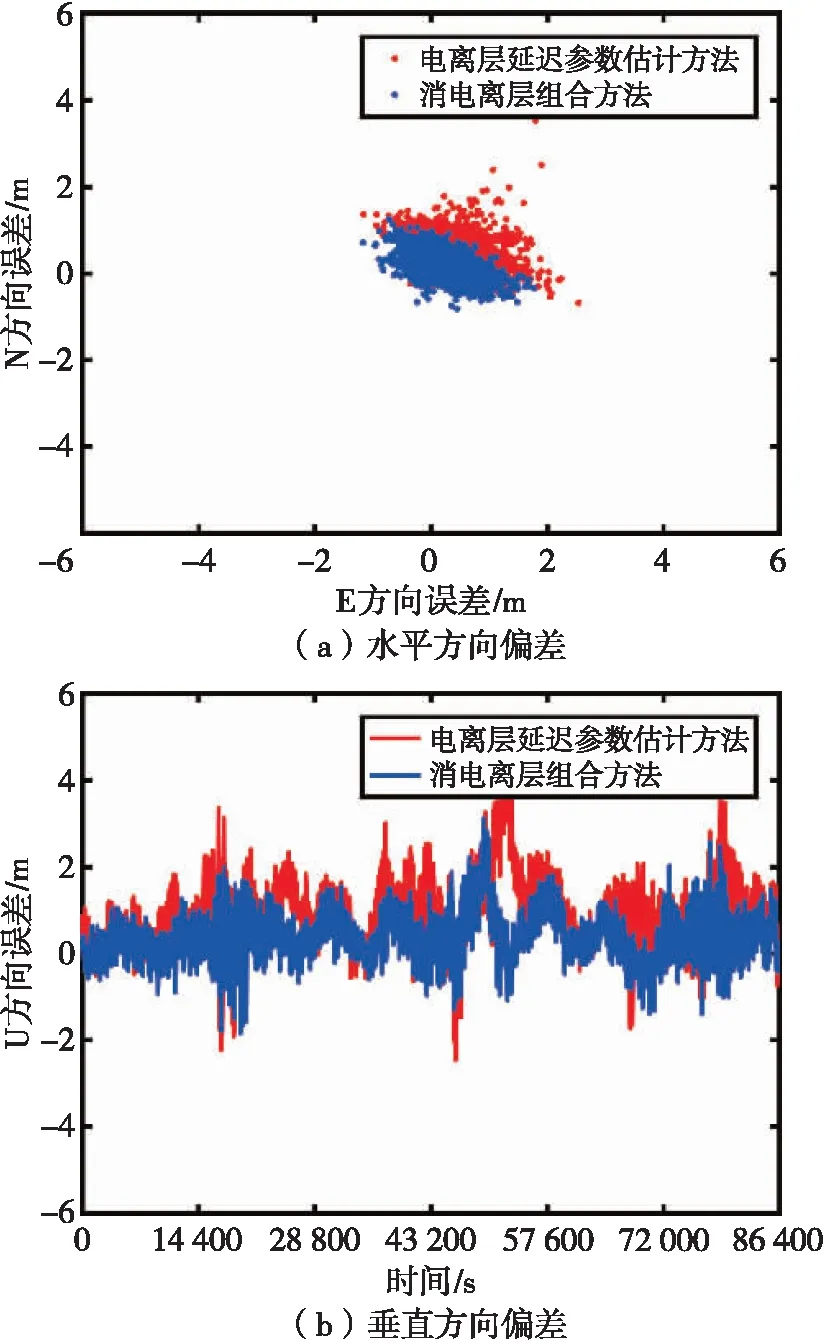
图3 基线1定位结果偏差

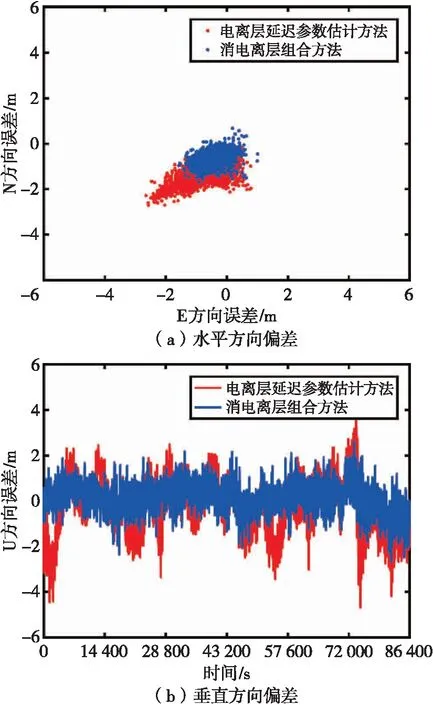
图4 基线2定位结果偏差

为了更直观地分析两种不同方法的定位结果差异,采用均方根误差(root mean square error, RMSE)指标对定位结果精度进行评定。表5和表6为北、东、天3个方向及水平方向具体的RMSE数值。可以发现,在 BDS-3水平方向上,基线1和基线2的四频IF组合方法的定位精度分别优于0.5和0.7 m,相较于电离层延迟参数估计方法分别提高了36.62%和44.32%;在垂直方向上,BDS-3两条基线的四频IF组合方法的定位精度均优于0.7 m,对于2条基线而言,四频IF组合方法定位精度较电离层延迟参数估计方法分别提高了42.42%和44.30%。

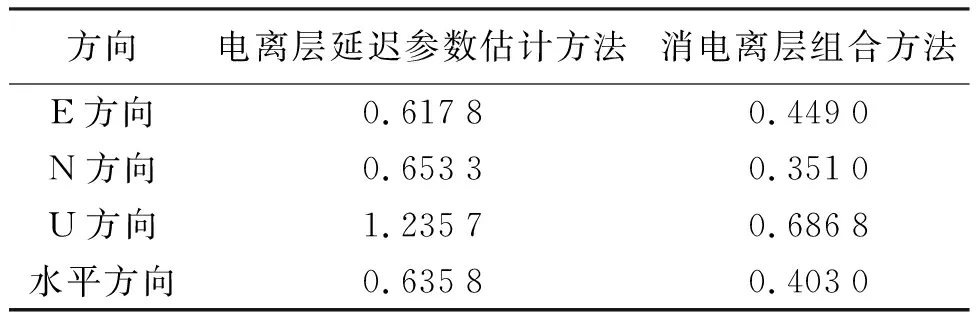
表5 基线1定位结果RMSE统计 m

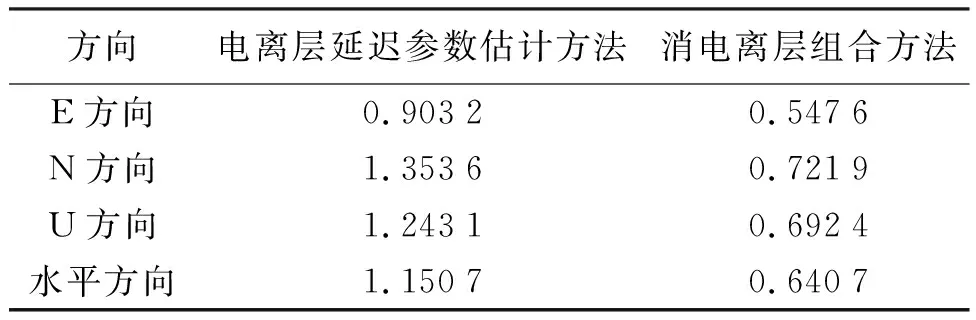
表6 基线2定位结果RMSE统计 m

电离层延迟参数估计方法虽然可以对电离层延迟进行估计,但是对于试验选用的2条超过500 km的长基线,基线两端测站的电离层时空分布不同且电离层自身又具有复杂性的情况,参数估计方法无法对电离层进行准确描述。图5为2条基线的电离层延迟量,可以发现,采用电离层延迟参数估计方法估计的电离层延迟量绝对值最大约为2 m,且整个观测时段波动幅度较大。而四频IF组合方法避开了对复杂电离层的参数估计,通过构造消电离层组合实现了电离层延迟的消除。

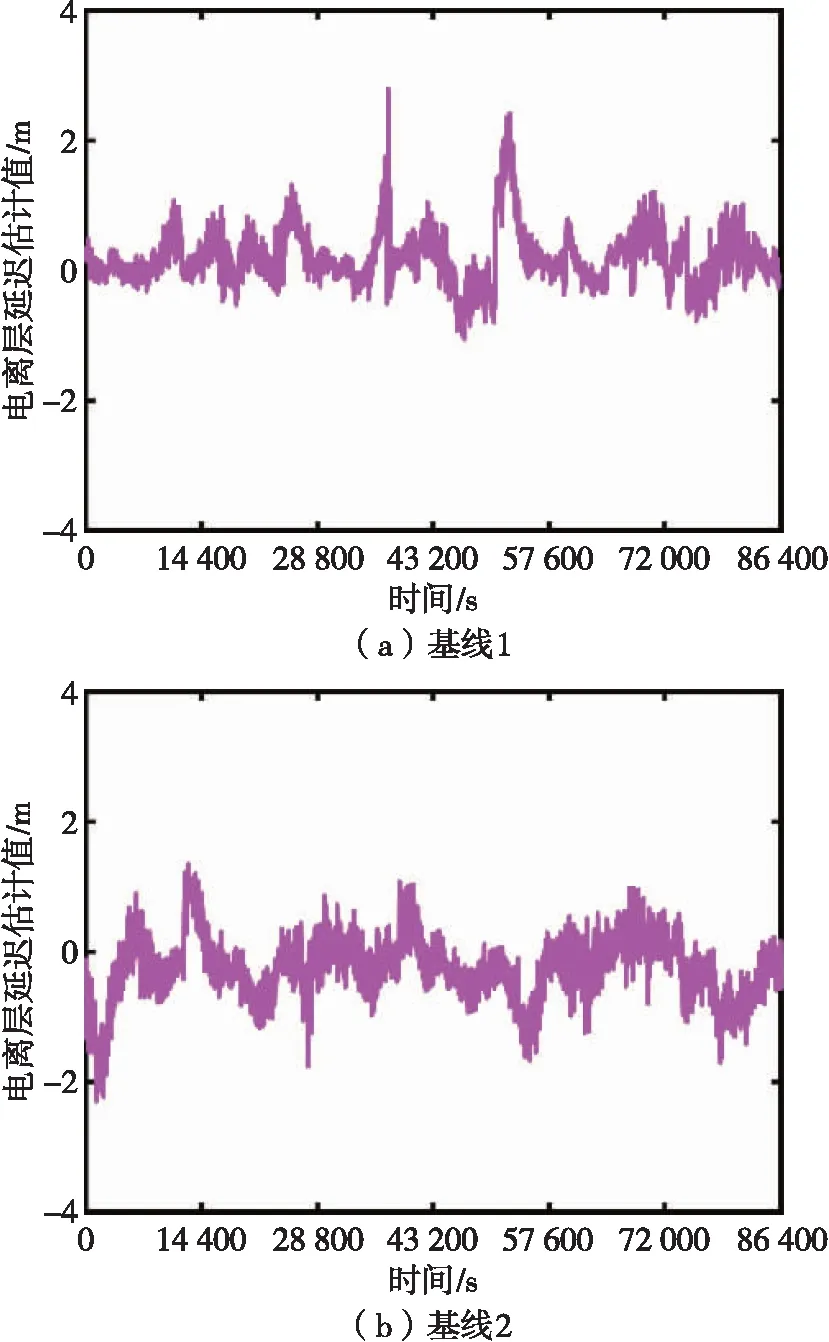
图5 电离层延迟估计值

对2条基线2021年年积日第199天至205天连续7天的水平和垂直方向定位结果RMSE值进行统计,分别如图6和图7所示。可知,当采用电离层延迟参数估计方法对基线1进行解算时,水平方向上定位精度保持在0.8 m以内,垂直方向达约1.4 m,而四频IF组合方法水平和垂直方向上定位精度可分别保持在0.5和0.7 m以内;对于基线2而言,电离层延迟参数估计方法的水平和垂直定位精度平均保持约1.2 m,而四频IF组合方法均可保持在0.7 m以内。可见随着基线长度的增加,定位精度下降。但是整体而言,四频IF组合方法较电离层延迟参数估计方法在水平和垂直方向上定位精度可分别提升35%和40%以上,定位结果得到明显改善。对于四频IF组合方法而言,可以使相对定位精度达1×10-9m,满足高精度相对定位要求。

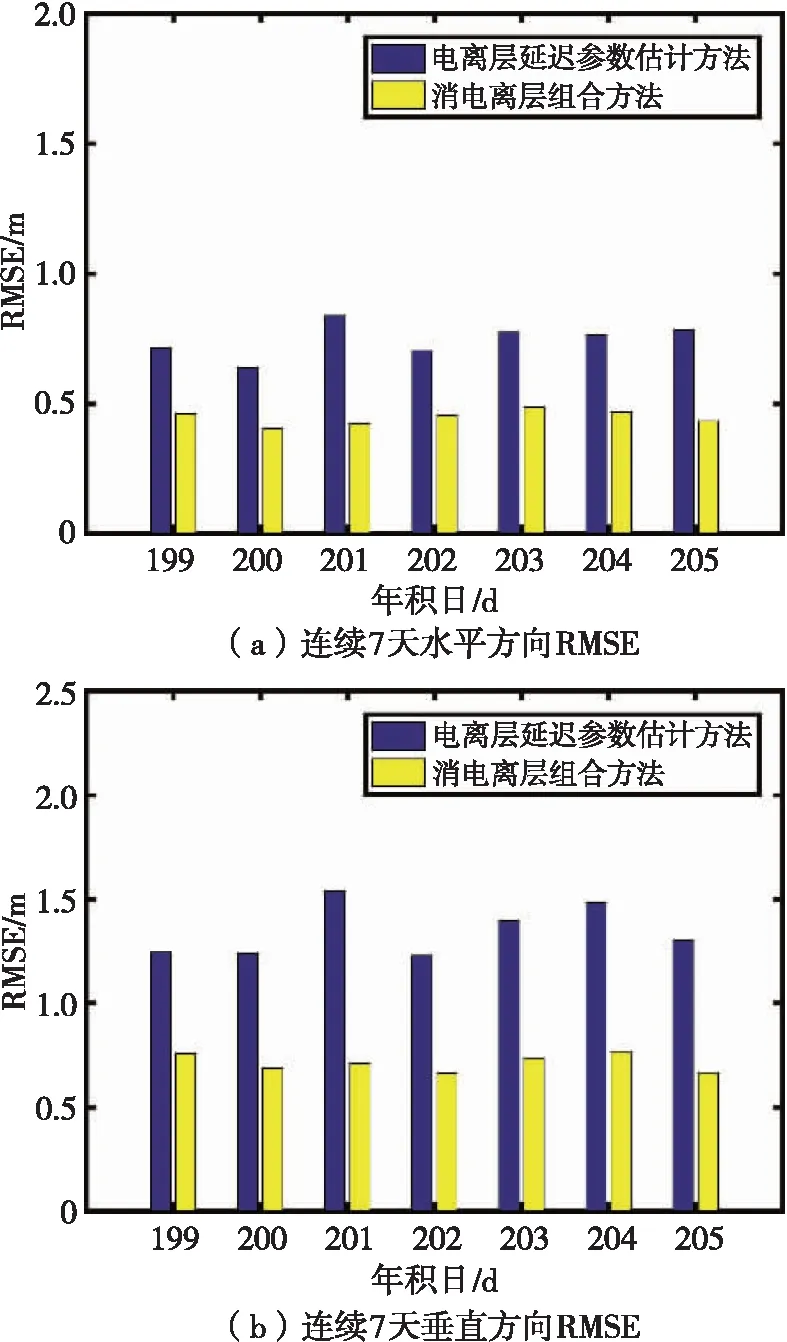
图6 基线1单天定位结果RMSE

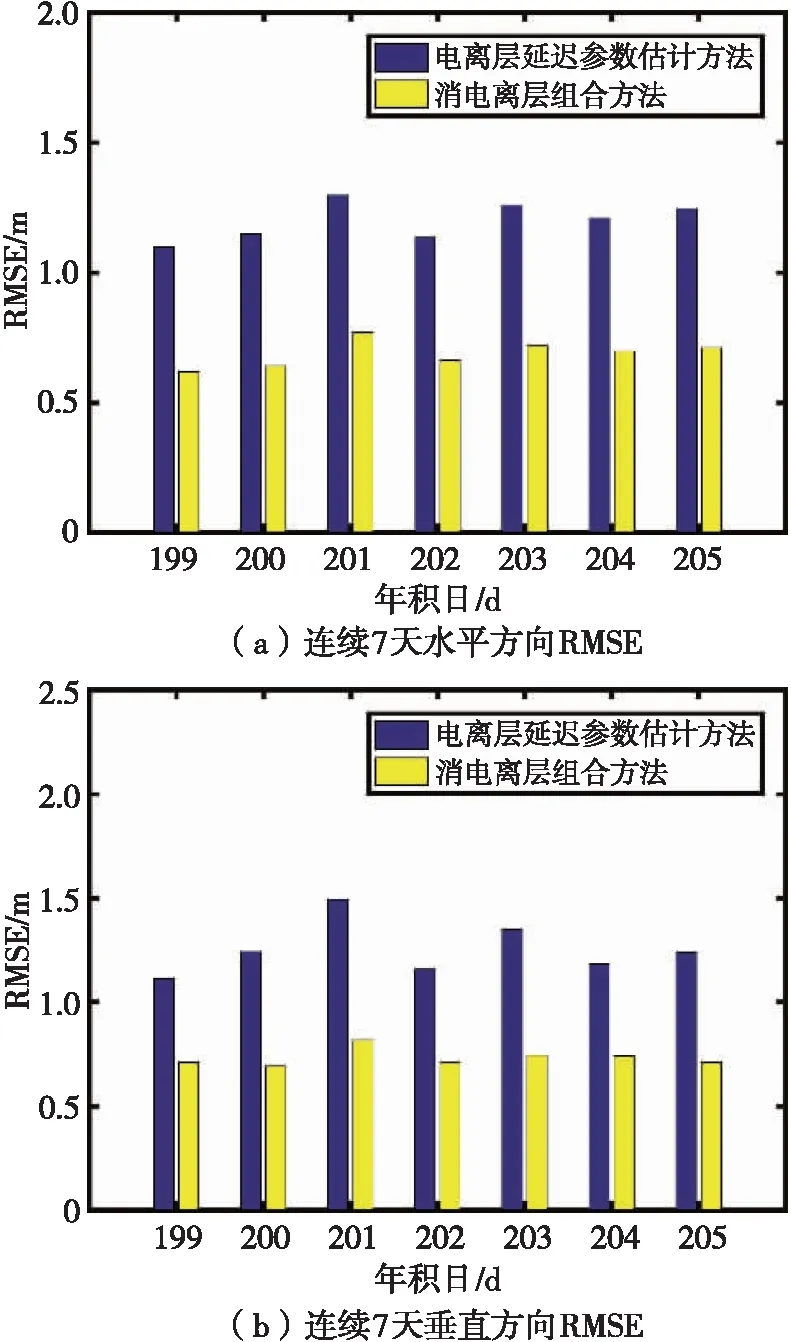
图7 基线2单天定位结果RMSE

5 结 语

本文针对BDS-3四频信号提出了一种四频IF组合方法,根据IGS提供的2条长基线数据进行对比,分析了四频IF组合方法与电离层参数估计方法的定位精度。试验结果表明,对于长度超过500 km的长基线,本文方法在水平和垂直方向定位精度均可达分米级,较电离层延迟参数估计方法的定位精度最大提升幅度可达35%和40%以上。其相对定位精度达1×10-9m,可以满足实际生产和科研的需要,这对于未来将基于多频信号的长基线定位技术应用于高精度定位领域提供了一定的参考。